人教版八年级数学下册 19.2.2 一次函数的应用 同步练习(含解析)
文档属性
| 名称 | 人教版八年级数学下册 19.2.2 一次函数的应用 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 559.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-01 16:18:57 | ||
图片预览




文档简介
19.2.2 一次函数-- 一次函数的应用
一、单选题:
1.“五一”期间,一体育用品商店搞优惠促销活动,其活动内容是:“凡在该商店一次性购物超过100元者,超过100元的部分按九折优惠”在此活动中,小东到该商店为学校一次性购买单价为70元的篮球个(),则小东应付货款(元)与篮球个数(个)的函数关系式是( )
A. B.
C. D.
2.自来水公司采用分段收费标准收水费,每月收取水费元与用水量之间的函数关系如图所示,琪琪家月份用水,应收水费( )
A.元 B.元 C.元 D.元
3.弹簧原长(不挂重物),弹簧总长与重物重量的关系如下表所示:
弹簧总长 16 17 18 19 20
重物重量 0.5 1.0 1.5 2.0 2.5
当重物重量为(在弹性限度内)时,弹簧总长L是( )
A. B. C. D.
4.如图是一支温度计的示意图,图中左边是用摄氏温度表示的温度值,右边是用华氏温度表示的温度值,下表是这两个温度值之间的部分对应关系:
摄氏温度值x/℃ 0 10 20 30 40 50
华氏温度值y/℉ 32 50 68 86 104 122
根据以上信息,可以得到y与x之间的关系式为( )
A. B. C. D.
5.某种藤类植物四个阶段的平均长度y()与生长时间x(天)的函数关系图象如图所示.当藤蔓长度大约在115时,植物进入浆果生长期,此时植物的生长天数是( )
A.90 B.95 C.140 D.143
6.如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图像由线段和射线组成,则一次购买6千克这种苹果比分六次购买1千克这种苹果可节省的金额为( )
A.5 B.6 C.7 D.8
7.如图,某电信公司手机的收费标准有两类,已知每月应缴费用(元)与通话时间(分)之间的关系如图所示,当通话时间为分钟时,按这两类收费标准缴费的差为( )
A.30元 B.20元 C.15元 D.10元
二、填空题:
8.“六·一”儿童节,学校六(1)班王老师带领班上名学生参观植物博览园.成人票单价20元,学生票单价10元.总费用(元)与的函数关系式为______.(不要求写自变量取值范围)
9.一辆汽车加满油后,油箱中有汽油,汽车行驶时正常的耗油量为,则油箱中剩余的汽油量关于加满后已驶里程的函数表达式是________,自变量的取值范围________.
10.某种储蓄的月利率为,如果存入2000元,不计利息税和复利,则本利和(元)与所存月数之间的函数关系式是_______________,10个月时本利和为___元.
11.某公司生产一种营养品,每日购进所需食材500千克,制成A,B两种包装的营养品,并恰好全部用完.信息如下表:
规格 每包食材含量 每包售价
A包装 1千克 45元
B包装 0.25千克 12元
已知生产的营养品当日全部售出.若A包装的数量不少于B包装的数量,则A为__________包时,每日所获总售价最大,最大总售价为__________元.
12.为了加强公民的节水意识,我市制定了如下用水收费标准:每户每月的用水不超过吨时,水价为每吨元;超过吨时,超过的部分按每吨元收费.现有某户居民月份用水吨,应交水费元,则关于的函数关系式是______.
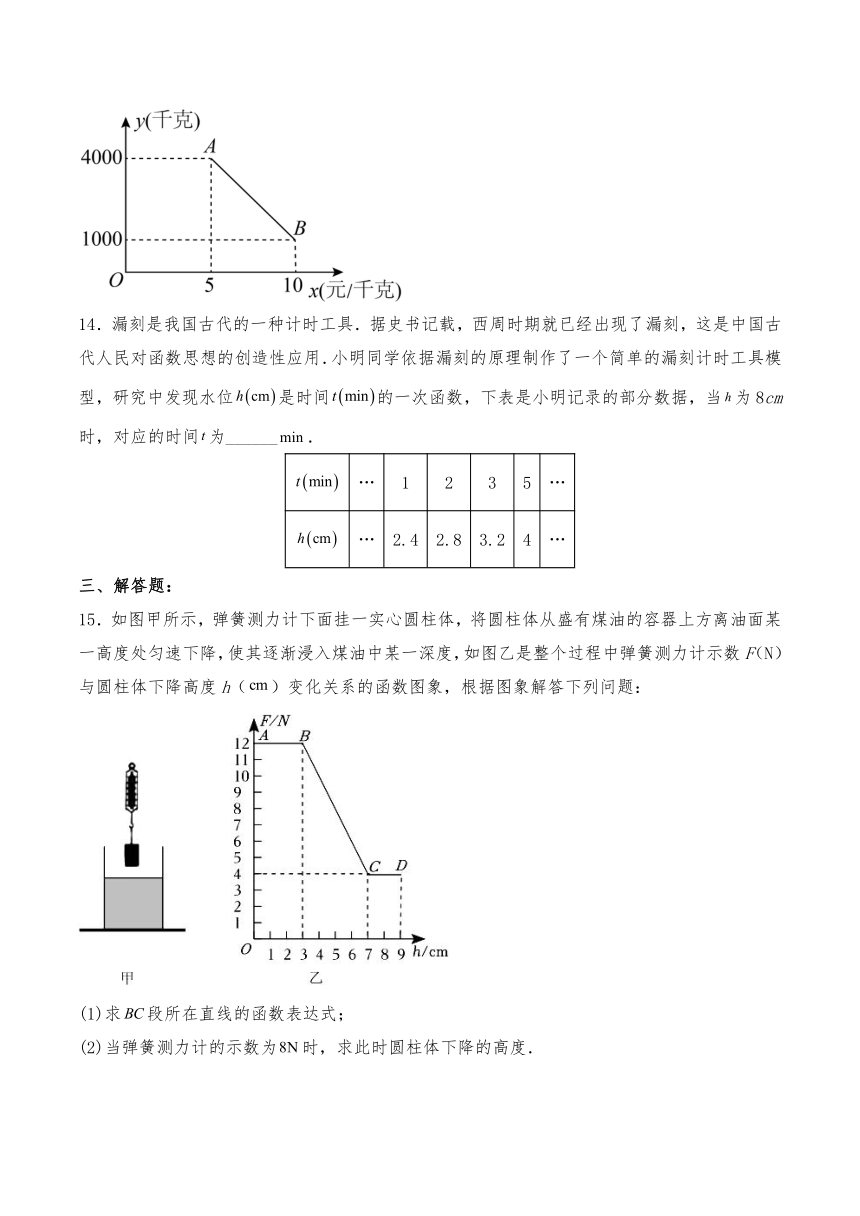
13.某苹果种植合作社通过网络销售苹果,如图所示的线段AB反映了苹果的日销售量y(千克)与销售单价x(元/千克)间的函数关系,已知1千克苹果的成本是5元,如果某天该合作社的苹果销售单价为8元/千克,那么这天销售苹果的盈利是 _____元.
14.漏刻是我国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用.小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位是时间的一次函数,下表是小明记录的部分数据,当为8cm时,对应的时间为______.
… 1 2 3 5 …
… 2.4 2.8 3.2 4 …
三、解答题:
15.如图甲所示,弹簧测力计下面挂一实心圆柱体,将圆柱体从盛有煤油的容器上方离油面某一高度处匀速下降,使其逐渐浸入煤油中某一深度,如图乙是整个过程中弹簧测力计示数F(N)与圆柱体下降高度h()变化关系的函数图象,根据图象解答下列问题:
(1)求段所在直线的函数表达式;
(2)当弹簧测力计的示数为时,求此时圆柱体下降的高度.
16.为增加校园绿化面积,某校计划购买甲、乙两种树苗100棵.已知购买20棵甲种树苗和16棵乙种树苗共花费1280元,购买1棵甲种树苗比1棵乙种树苗多花费10元.
(1)求甲、乙两种树苗每棵的价格分别是多少元?
(2)若购买甲树苗不少于25棵,则购买甲、乙两种树苗各多少棵时花费最少?最少费用是多少元?
17.某一蔬菜经营商从蔬菜批发市场批发了黄瓜和茄子共千克到菜市场去卖,黄瓜和茄子当天的批发价与零售价如表所示:
品名 黄瓜 茄子
批发价(元/千克)
零售价(元/千克)
(1)若批发黄瓜和茄子共花元,则黄瓜和茄子各多少千克?
(2)设批发了黄瓜千克,卖完这批黄瓜和茄子的利润是元,求与的函数关系式.
18.为了合理利用防疫物资,省防疫指挥部积极在各个地区之间进行物资调配,甲、乙两辆车沿相同的路线由A地到B地匀速前进,A,B两地间的路程为,甲、乙两车前进的路程分别为、,甲车出发后的时间为,甲、乙两车前进的路程与时间的函数图象如图所示,根据图象信息回答下列问题:
(1)甲的速度是________,乙比甲晚出发_________h;
(2)请你分别求出甲、乙两人前进的路程、与甲出发后的时间之间的函数关系式;
(3)甲经过多长时间被乙追上?此时两人距离B地还有多远?
答案
一、单选题:
1.C
【分析】根据已知表示出买x个篮球的总钱数以及优惠后价格,进而得出等式即可.
【详解】解:∵凡在该商店一次性购物超过 100元者,超过100元的部分按九折优惠,
∴小东到该商店为学校一次性购买单价为70元的篮球x个(x>2),
则小东应付货款y(元)与篮球个数x(个)的函数关系式是:
y=(70x-100)×0.9+100=63x+10(x>2),
故选:C.
2.C
【分析】设当时,关于的函数关系式为,根据函数图象上点的坐标特征利用待定系数法即可求出关于的函数关系式,再将代入其内求出的值,此题得解.
【详解】解:设当时,关于的函数关系式为,
将、代入中,
则,
解得 ,
当时,关于的函数关系式为,
当时,,
琪琪家月份应交水费元,
故选:C.
3.D
【分析】根据表格数据,建立数学模型,进而利用待定系数法可得函数关系式,当x=5时,代入函数解析式求值即可.
【详解】解:根据题意得:弹簧总长与重物重量是一次函数的关系,
设弹簧总长与重物重量函数关系式为,
把(0.5,16),(1.0,17)代入得:
,解得:,
∴弹簧总长与重物重量函数关系式为,
当时,,
即当重物重量为(在弹性限度内)时,弹簧总长L是26cm.
故选:D
4.A
【分析】观察表格中的对应数据的特征可知:摄氏温度每增加,华氏温度就增加,因此可判断y与x之间是一次函数的关系,设一次函数表达式为,把,代入计算即可.
【详解】解:由表格中的对应数据的特征可知:摄氏温度每增加,华氏温度就增加,因此可判断y与x之间是一次函数的关系,
设一次函数表达式为,把,代入得:,
解得:,
,
故选:A.
5.B
【分析】利用待定系数法求出20<x≤120时y与x之间的函数关系式,再把y=115代入计算即可求解.
【详解】解:设20<x≤120时,y=kx+b,根据题意得:
,
解得,
∴y=1.4x-18,
当y=115时,1.4x-18=115,
解得x=95,
即此时植物的生长天数是95天.
故选:B.
6.D
【分析】观察函数图象找出点的坐标,利用待定系数法求出线段和设的函数关系式,再分别求出当和时,y的值,用即可求出一次购买6千克这种苹果比分六次购买1千克这种苹果节省的钱数.
【详解】解:设y关于x的函数关系式为,
当时,将、代入中,
,
解得:,
∴;
当时,将,代入中,
,
解得:,
∴.
当时,,
当时,,
(元),
故选D.
7.D
【分析】根据题意,待定系数法求得解析式,分别令,求得是的值,进而即可求解.
【详解】解:设类收费的解析式为,代入 ,,
得,
解得,
∴,
类收费的解析式为,代入,
得,
解得,
∴,
∴当时,,,
∴(元),
故选:D.
二、填空题:
8.y=10x+20
【分析】根据总费用=学生费用+老师费用列出函数关系式即可.
【详解】解:由题意得:y=10x+20,
故答案为:y=10x+20.
9.
【分析】根据题意,找到等量关系,求出函数关系,即可求解.
【详解】解:原有油量,用油量,
由题意得:油箱中剩余的汽油两关于加满后已驶里程的函数表达式是,
自变量d的取值范围为:.
故答案为:,.
10. 2040
【分析】根据题意可求出存月后的利息为,进而即可得出本利和(元)与所存月数之间的函数关系式.再将代入所求解析式即可求解.
【详解】解:存月后的利息为,
.
当时,.
故答案为:;2040.
11. 400 22800
【分析】设A包装的数量为x包,B包装数量为y包,总售价为W元,根据题意列出y与x的关系和W与x的函数关系式,利用一次函数的性质求解即可.
【详解】解:设A包装的数量为x包,B包装数量为y包,总售价为W元,
根据题意,得:,
∴y=-4x+2000,
由x≥-4x+2000得:x≥400,
∴W=45x+12y=45x+12(-4x+2000)=-3x+24000,
∵-3<0,
∴W随x的增大而减小,
∴当x=400时,W最大,最大为-3×400+24000=22800(元),
故答案为:400,22800.
12./
【分析】由已知得水费吨的水费超过10吨的水费,由此可列出一次函数关系式.
【详解】解:依题意有.
所以y关于x的函数关系式是.
故答案为:.
13.6600
【分析】求出AB的解析式,将x=8代入可得这天销售苹果的日销售量,即可求得这天销售苹果的盈利.
【详解】解:设AB的解析式是y=kx+b,
∴,解得,
即苹果日销售量y(千克)与苹果售价x(元)的函数解析式是y=-600x+7000(5≤x≤10),
x=8时,苹果日销售量y=-600×8+7000=2200,
∴这天销售苹果的盈利是2200×(8-5)=6600(元).
故答案为:6600.
14.15
【分析】先根据一次函数的性质判断出错误的h值,再利用待定系数法求出h与t的关系式,最后将h=8代入即可.
【详解】解:设一次函数的表达式为h=kt+b,t每增加一个单位h增加或减少k个单位,
∴由表可知,当t=3时,h的值记录错误.
将(1,2.4)(2,2.8)代入得,
,
解得k=0.4,b=2,
∴h=0.4t+2,
将h=8代入得,t=15.
故答案为:15.
三、解答题:
15.(1)解:设段所在直线的函数表达式为,根据题意得:
,
解得,
∴段所在直线的函数表达式为;
(2)当时,,
解得,
答:此时圆柱体下降的高度为.
16.(1)解:设甲种树苗每棵的价格是元,乙种树苗每棵的价格是元,
根据题意得:,
解得,
答:甲种树苗每棵的价格是40元,乙种树苗每棵的价格是30元;
(2)设购买两种树苗共花费元,购买甲种树苗棵,则购买乙种树苗棵,
∵购买甲树苗不少于25棵,
∴,
根据题意:,
,
随的增大而增大,
时,取最小值,最小值为(元),
此时,
∴购买甲种树苗25棵,乙种树苗75棵,花费最少,最少费用是元.
17.(1)解:设批发黄瓜千克,则批发茄子千克,
由题意可得:,
解得,
(千克),
答:批发黄瓜千克,批发茄子千克;
(2)解:由题意可得,
,
即与的函数关系式是.
18.(1)解:甲的速度是;
乙比甲晚出发;
故答案为:50;1.
(2)解:设甲、乙两人前进的路程、与甲出发后的时间之间的函数关系式分别为:,,
把代入得:,
解得:,
∴;
把,代入得:,
解得:,
∴;
(3)解:令,
解得:,
∴甲经过被乙追上;
把代入得:,
,
∴此时两人距离B地还有.
一、单选题:
1.“五一”期间,一体育用品商店搞优惠促销活动,其活动内容是:“凡在该商店一次性购物超过100元者,超过100元的部分按九折优惠”在此活动中,小东到该商店为学校一次性购买单价为70元的篮球个(),则小东应付货款(元)与篮球个数(个)的函数关系式是( )
A. B.
C. D.
2.自来水公司采用分段收费标准收水费,每月收取水费元与用水量之间的函数关系如图所示,琪琪家月份用水,应收水费( )
A.元 B.元 C.元 D.元
3.弹簧原长(不挂重物),弹簧总长与重物重量的关系如下表所示:
弹簧总长 16 17 18 19 20
重物重量 0.5 1.0 1.5 2.0 2.5
当重物重量为(在弹性限度内)时,弹簧总长L是( )
A. B. C. D.
4.如图是一支温度计的示意图,图中左边是用摄氏温度表示的温度值,右边是用华氏温度表示的温度值,下表是这两个温度值之间的部分对应关系:
摄氏温度值x/℃ 0 10 20 30 40 50
华氏温度值y/℉ 32 50 68 86 104 122
根据以上信息,可以得到y与x之间的关系式为( )
A. B. C. D.
5.某种藤类植物四个阶段的平均长度y()与生长时间x(天)的函数关系图象如图所示.当藤蔓长度大约在115时,植物进入浆果生长期,此时植物的生长天数是( )
A.90 B.95 C.140 D.143
6.如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图像由线段和射线组成,则一次购买6千克这种苹果比分六次购买1千克这种苹果可节省的金额为( )
A.5 B.6 C.7 D.8
7.如图,某电信公司手机的收费标准有两类,已知每月应缴费用(元)与通话时间(分)之间的关系如图所示,当通话时间为分钟时,按这两类收费标准缴费的差为( )
A.30元 B.20元 C.15元 D.10元
二、填空题:
8.“六·一”儿童节,学校六(1)班王老师带领班上名学生参观植物博览园.成人票单价20元,学生票单价10元.总费用(元)与的函数关系式为______.(不要求写自变量取值范围)
9.一辆汽车加满油后,油箱中有汽油,汽车行驶时正常的耗油量为,则油箱中剩余的汽油量关于加满后已驶里程的函数表达式是________,自变量的取值范围________.
10.某种储蓄的月利率为,如果存入2000元,不计利息税和复利,则本利和(元)与所存月数之间的函数关系式是_______________,10个月时本利和为___元.
11.某公司生产一种营养品,每日购进所需食材500千克,制成A,B两种包装的营养品,并恰好全部用完.信息如下表:
规格 每包食材含量 每包售价
A包装 1千克 45元
B包装 0.25千克 12元
已知生产的营养品当日全部售出.若A包装的数量不少于B包装的数量,则A为__________包时,每日所获总售价最大,最大总售价为__________元.
12.为了加强公民的节水意识,我市制定了如下用水收费标准:每户每月的用水不超过吨时,水价为每吨元;超过吨时,超过的部分按每吨元收费.现有某户居民月份用水吨,应交水费元,则关于的函数关系式是______.
13.某苹果种植合作社通过网络销售苹果,如图所示的线段AB反映了苹果的日销售量y(千克)与销售单价x(元/千克)间的函数关系,已知1千克苹果的成本是5元,如果某天该合作社的苹果销售单价为8元/千克,那么这天销售苹果的盈利是 _____元.
14.漏刻是我国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用.小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位是时间的一次函数,下表是小明记录的部分数据,当为8cm时,对应的时间为______.
… 1 2 3 5 …
… 2.4 2.8 3.2 4 …
三、解答题:
15.如图甲所示,弹簧测力计下面挂一实心圆柱体,将圆柱体从盛有煤油的容器上方离油面某一高度处匀速下降,使其逐渐浸入煤油中某一深度,如图乙是整个过程中弹簧测力计示数F(N)与圆柱体下降高度h()变化关系的函数图象,根据图象解答下列问题:
(1)求段所在直线的函数表达式;
(2)当弹簧测力计的示数为时,求此时圆柱体下降的高度.
16.为增加校园绿化面积,某校计划购买甲、乙两种树苗100棵.已知购买20棵甲种树苗和16棵乙种树苗共花费1280元,购买1棵甲种树苗比1棵乙种树苗多花费10元.
(1)求甲、乙两种树苗每棵的价格分别是多少元?
(2)若购买甲树苗不少于25棵,则购买甲、乙两种树苗各多少棵时花费最少?最少费用是多少元?
17.某一蔬菜经营商从蔬菜批发市场批发了黄瓜和茄子共千克到菜市场去卖,黄瓜和茄子当天的批发价与零售价如表所示:
品名 黄瓜 茄子
批发价(元/千克)
零售价(元/千克)
(1)若批发黄瓜和茄子共花元,则黄瓜和茄子各多少千克?
(2)设批发了黄瓜千克,卖完这批黄瓜和茄子的利润是元,求与的函数关系式.
18.为了合理利用防疫物资,省防疫指挥部积极在各个地区之间进行物资调配,甲、乙两辆车沿相同的路线由A地到B地匀速前进,A,B两地间的路程为,甲、乙两车前进的路程分别为、,甲车出发后的时间为,甲、乙两车前进的路程与时间的函数图象如图所示,根据图象信息回答下列问题:
(1)甲的速度是________,乙比甲晚出发_________h;
(2)请你分别求出甲、乙两人前进的路程、与甲出发后的时间之间的函数关系式;
(3)甲经过多长时间被乙追上?此时两人距离B地还有多远?
答案
一、单选题:
1.C
【分析】根据已知表示出买x个篮球的总钱数以及优惠后价格,进而得出等式即可.
【详解】解:∵凡在该商店一次性购物超过 100元者,超过100元的部分按九折优惠,
∴小东到该商店为学校一次性购买单价为70元的篮球x个(x>2),
则小东应付货款y(元)与篮球个数x(个)的函数关系式是:
y=(70x-100)×0.9+100=63x+10(x>2),
故选:C.
2.C
【分析】设当时,关于的函数关系式为,根据函数图象上点的坐标特征利用待定系数法即可求出关于的函数关系式,再将代入其内求出的值,此题得解.
【详解】解:设当时,关于的函数关系式为,
将、代入中,
则,
解得 ,
当时,关于的函数关系式为,
当时,,
琪琪家月份应交水费元,
故选:C.
3.D
【分析】根据表格数据,建立数学模型,进而利用待定系数法可得函数关系式,当x=5时,代入函数解析式求值即可.
【详解】解:根据题意得:弹簧总长与重物重量是一次函数的关系,
设弹簧总长与重物重量函数关系式为,
把(0.5,16),(1.0,17)代入得:
,解得:,
∴弹簧总长与重物重量函数关系式为,
当时,,
即当重物重量为(在弹性限度内)时,弹簧总长L是26cm.
故选:D
4.A
【分析】观察表格中的对应数据的特征可知:摄氏温度每增加,华氏温度就增加,因此可判断y与x之间是一次函数的关系,设一次函数表达式为,把,代入计算即可.
【详解】解:由表格中的对应数据的特征可知:摄氏温度每增加,华氏温度就增加,因此可判断y与x之间是一次函数的关系,
设一次函数表达式为,把,代入得:,
解得:,
,
故选:A.
5.B
【分析】利用待定系数法求出20<x≤120时y与x之间的函数关系式,再把y=115代入计算即可求解.
【详解】解:设20<x≤120时,y=kx+b,根据题意得:
,
解得,
∴y=1.4x-18,
当y=115时,1.4x-18=115,
解得x=95,
即此时植物的生长天数是95天.
故选:B.
6.D
【分析】观察函数图象找出点的坐标,利用待定系数法求出线段和设的函数关系式,再分别求出当和时,y的值,用即可求出一次购买6千克这种苹果比分六次购买1千克这种苹果节省的钱数.
【详解】解:设y关于x的函数关系式为,
当时,将、代入中,
,
解得:,
∴;
当时,将,代入中,
,
解得:,
∴.
当时,,
当时,,
(元),
故选D.
7.D
【分析】根据题意,待定系数法求得解析式,分别令,求得是的值,进而即可求解.
【详解】解:设类收费的解析式为,代入 ,,
得,
解得,
∴,
类收费的解析式为,代入,
得,
解得,
∴,
∴当时,,,
∴(元),
故选:D.
二、填空题:
8.y=10x+20
【分析】根据总费用=学生费用+老师费用列出函数关系式即可.
【详解】解:由题意得:y=10x+20,
故答案为:y=10x+20.
9.
【分析】根据题意,找到等量关系,求出函数关系,即可求解.
【详解】解:原有油量,用油量,
由题意得:油箱中剩余的汽油两关于加满后已驶里程的函数表达式是,
自变量d的取值范围为:.
故答案为:,.
10. 2040
【分析】根据题意可求出存月后的利息为,进而即可得出本利和(元)与所存月数之间的函数关系式.再将代入所求解析式即可求解.
【详解】解:存月后的利息为,
.
当时,.
故答案为:;2040.
11. 400 22800
【分析】设A包装的数量为x包,B包装数量为y包,总售价为W元,根据题意列出y与x的关系和W与x的函数关系式,利用一次函数的性质求解即可.
【详解】解:设A包装的数量为x包,B包装数量为y包,总售价为W元,
根据题意,得:,
∴y=-4x+2000,
由x≥-4x+2000得:x≥400,
∴W=45x+12y=45x+12(-4x+2000)=-3x+24000,
∵-3<0,
∴W随x的增大而减小,
∴当x=400时,W最大,最大为-3×400+24000=22800(元),
故答案为:400,22800.
12./
【分析】由已知得水费吨的水费超过10吨的水费,由此可列出一次函数关系式.
【详解】解:依题意有.
所以y关于x的函数关系式是.
故答案为:.
13.6600
【分析】求出AB的解析式,将x=8代入可得这天销售苹果的日销售量,即可求得这天销售苹果的盈利.
【详解】解:设AB的解析式是y=kx+b,
∴,解得,
即苹果日销售量y(千克)与苹果售价x(元)的函数解析式是y=-600x+7000(5≤x≤10),
x=8时,苹果日销售量y=-600×8+7000=2200,
∴这天销售苹果的盈利是2200×(8-5)=6600(元).
故答案为:6600.
14.15
【分析】先根据一次函数的性质判断出错误的h值,再利用待定系数法求出h与t的关系式,最后将h=8代入即可.
【详解】解:设一次函数的表达式为h=kt+b,t每增加一个单位h增加或减少k个单位,
∴由表可知,当t=3时,h的值记录错误.
将(1,2.4)(2,2.8)代入得,
,
解得k=0.4,b=2,
∴h=0.4t+2,
将h=8代入得,t=15.
故答案为:15.
三、解答题:
15.(1)解:设段所在直线的函数表达式为,根据题意得:
,
解得,
∴段所在直线的函数表达式为;
(2)当时,,
解得,
答:此时圆柱体下降的高度为.
16.(1)解:设甲种树苗每棵的价格是元,乙种树苗每棵的价格是元,
根据题意得:,
解得,
答:甲种树苗每棵的价格是40元,乙种树苗每棵的价格是30元;
(2)设购买两种树苗共花费元,购买甲种树苗棵,则购买乙种树苗棵,
∵购买甲树苗不少于25棵,
∴,
根据题意:,
,
随的增大而增大,
时,取最小值,最小值为(元),
此时,
∴购买甲种树苗25棵,乙种树苗75棵,花费最少,最少费用是元.
17.(1)解:设批发黄瓜千克,则批发茄子千克,
由题意可得:,
解得,
(千克),
答:批发黄瓜千克,批发茄子千克;
(2)解:由题意可得,
,
即与的函数关系式是.
18.(1)解:甲的速度是;
乙比甲晚出发;
故答案为:50;1.
(2)解:设甲、乙两人前进的路程、与甲出发后的时间之间的函数关系式分别为:,,
把代入得:,
解得:,
∴;
把,代入得:,
解得:,
∴;
(3)解:令,
解得:,
∴甲经过被乙追上;
把代入得:,
,
∴此时两人距离B地还有.
