人教版八年级数学下册 19.3 课题学习 选择方案 同步练习(含解析)
文档属性
| 名称 | 人教版八年级数学下册 19.3 课题学习 选择方案 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 477.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-01 16:21:46 | ||
图片预览


文档简介
19.3 课题学习 选择方案
一、单选题:
1.某公司手机话费收费有 套餐(月租费 元,通话费每分钟 元)和 套餐(月租费 元,通话费每分钟 元)两种.当月通话时间为( )时,, 两种套餐收费一样.
A. 分钟 B. 分钟 C. 分钟 D. 分钟
2.网红“脏脏包”是时下最流行的一款面包,“脏脏包”正如其名,它看起来脏脏的,吃完以后嘴巴和手上会因沾上巧克力而变“脏”,因而得名“脏脏包”.某面包店每天固定制作甲、乙两种款型的脏脏包共200个,且所有脏脏包当天全部售出,原料成本、销售单价及店员生产提成如表所示:
甲(元/个) 乙(元/个)
原料成本 12 8
销售单价 18 12
生产提成 1 0.6
设该店每天制作甲款型的脏脏包x(个),每天获得的总利润为y(元).则y与x之间的函数关系式为( )
A.y=1.6x+680 B.y=﹣1.6x+680
C.y=﹣1.6x﹣680 D.y=﹣1.6x﹣6800
3.水果店购买一种葡萄所付款金额(元)与购买量(千克)情况如图,萌萌一次购买6千克这种葡萄比她分三次购买每次购2千克这种葡萄可节省( )元.
A.18 B.12 C.9 D.6
4.某电脑公司经营A,B两种台式电脑,分析过去的销售记录可以知道:每台A型电脑可盈利200元,每台B型电脑可盈利300元;在同一时期内,A型电脑的销售量不小于B型电脑销售量的4倍.已知该公司在同一时期内销售这两种电脑共210台,则该公司在这一时期内销售这两种电脑能获得的最大利润是( )
A.42000元 B.46200元 C.52500元 D.63000元
5.某游泳馆新推出了甲、乙两种消费卡,设游泳次数为时两种消费卡所需费用分别为,元,,与的函数图象如图所示,当游泳次数为30次时选择哪种消费卡更合算( )
A.甲种更合算 B.乙种更合算 C.两种一样合算 D.无法确定
6.如图,某电信公司提供了,两种方案的移动通讯费用(元)与通话时间(分)之间的关系,则以下说法正确的是( )
①若通话时间少于120分,则方案比方案便宜
②若通话时间超过200分,则方案比方案便宜
③通讯费用为60元,则方案比方案的通话时间多
④当通话时间是170分钟/时,两种方案通讯费用相等
A.1个 B.2个 C.3个 D.4个
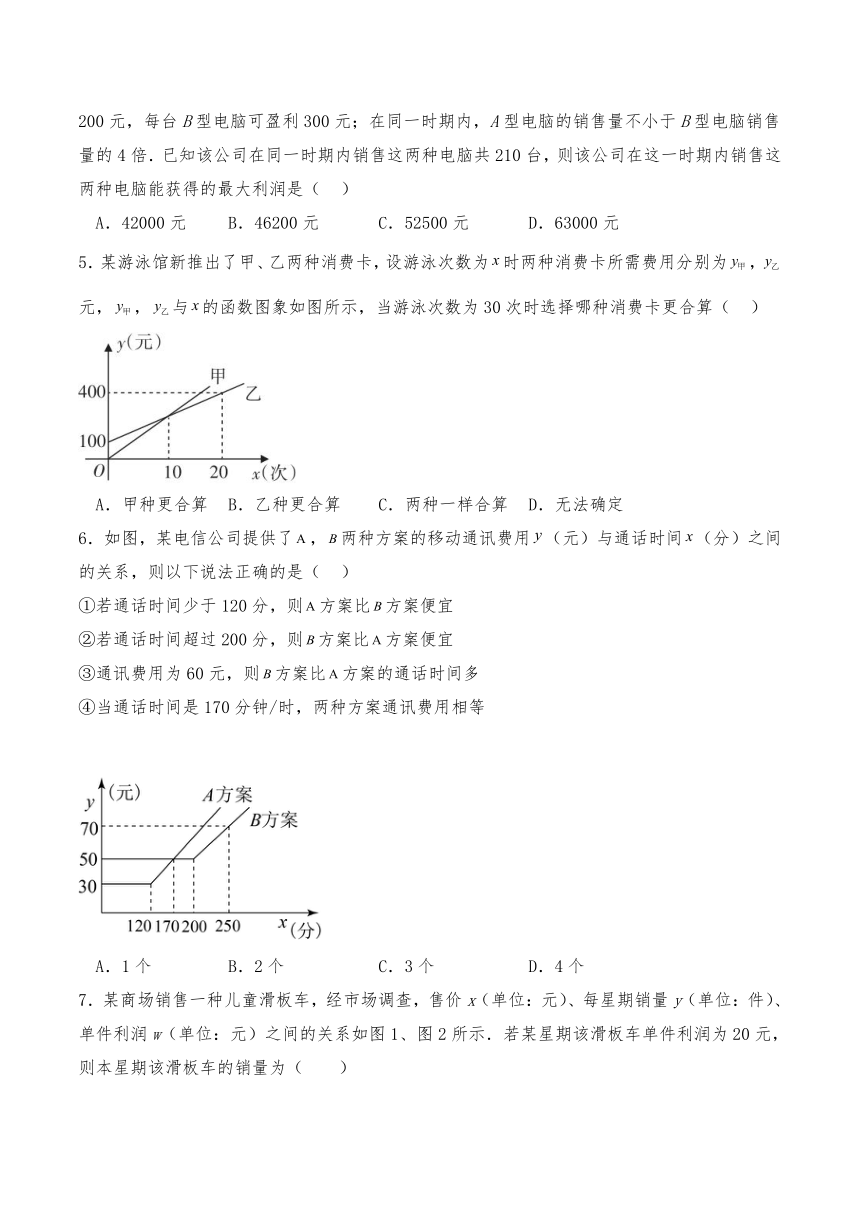
7.某商场销售一种儿童滑板车,经市场调查,售价x(单位:元)、每星期销量y(单位:件)、单件利润w(单位:元)之间的关系如图1、图2所示.若某星期该滑板车单件利润为20元,则本星期该滑板车的销量为( )
A.94 B.96 C.1600 D.1800
二、填空题:
8.元旦期间,大兴商场搞优惠活动,其活动内容是:凡在本商场一次性购买商品超过100元者,超过100元的部分按8折优惠.在此活动中,小明到该商场一次性购买单价为60元的礼盒()件,则应付款(元)与商品数(件)之间的关系式,化简后的结果是______.
9.某苹果种植合作社通过网络销售苹果,图中线段为苹果日销售量(千克)与苹果售价(元)的函数图像的一部分.已知1千克苹果的成本价为5元,如果某天以8元/千克的价格销售苹果,那么这天销售苹果的盈利是_____元.
10.假期学校组织360名师生外出旅游,某客车出租公司有两种大客车可供选择:甲种客车每辆车有40个座,租金400元;乙种客车每辆车有50个座,租金480元.则租用该公司客车最少需用租金__ 元.
11.某公司生产一种营养品,每日购进所需食材500千克,制成A,B两种包装的营养品,并恰好全部用完.信息如下表:
规格 每包食材含量 每包售价
A包装 1千克 45元
B包装 0.25千克 12元
已知生产的营养品当日全部售出.若A包装的数量不少于B包装的数量,则A为__________包时,每日所获总售价最大,最大总售价为__________元.
12.某饮料厂生产一种饮料,经测算,用1吨水生产的饮料所获利润y(元)与1吨水的买入价x(元)的关系如下表:
1吨水的买入价x(元) 2 4 6 8 10
利润y(元) 202 200 198 196 194
当1吨水生产的饮料所获的利润为197元时,买入10吨水共需______元.
13.某手工作坊生产并销售某种食品,假设销售量与产量相等,如图中的线段AB、OC分别表示每天生产成本(单位:元)、收入(单位:元)与产量x(单位:千克)之间的函数关系.若该手工作坊某一天既不盈利也不亏损,则这天的产量是______千克.
三、解答题:
14.乡村振兴作为“十四五”期间的重要战略,受到了广大人民群众的关注.党的二十大再次对全面推进乡村振兴进行部署.为了发展乡村特色产业,百花村花费3000元集中采购了甲种树苗700株,乙种树苗400株,已知乙种树苗单价是甲种树苗单价的2倍.
(1)求甲、乙两种树苗的单价分别是多少元?
(2)百花村决定再购买同样的两种树苗100株用于补充栽种.其中甲种树苗不多于33株,在单价不变,总费用不超过340元的情况下,最低费用是多少元?
15.为弘扬爱国精神,传承民族文化,某校组织了“诗词里的中国”主题比赛,计划去某超市购买A,B两种奖品共300个,A种奖品每个20元,B种奖品每个15元,该超市对同时购买这两种奖品的顾客有两种销售方案(只能选择其中一种).
方案一:A种奖品每个打九折,B种奖品每个打六折.
方案二:A,B两种奖品均打八折.
设购买A种奖品x个,选择方案一的购买费用为元,选择方案二的购买费用为元.
(1)请分别写出、与x之间的函数关系式.
(2)请你计算该校选择哪种方案支付的费用较少.
16.某地计划修建一条长36千米的乡村公路,已知甲工程队修路的速度是乙工程队修路速度的倍,乙工程队单独完成本次修路任务比甲工程队单独完成多20天.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)已知甲工程队修路费用为25万元/千米,乙工程队修路费用为20万元/千米.甲工程队先单独修路若干天后,接到其它任务需要离开,剩下的工程由乙工程队单独完成.若要使修路总时间不超过55天,总费用不超过820万元,且甲工程队所修路程需为整数,请问共有几种修路方案?哪种方案最省钱?
17.“双减”政策颁布后,各校重视了延迟服务,并在延迟服务中加大了体育活动的力度.某体育用品商店抓住商机,计划购进300套乒乓球拍和羽毛球拍进行销售,其中购进乒乓球拍的套数不超过150套,它们的进价和售价如下表:
进价 售价
乒乓球拍(元/套) a 50
羽毛球拍(元/套) b 60
已知购进2套乒乓球拍和1套羽毛球拍需花费110元,购进4套乒乓球拍和3套羽毛球拍需花费260元.
(1)求出a,b的值;
(2)该面店根据以往销售经验,决定购进乒乓球拍套数不少于羽毛球拍套数的一半,设购进乒乓球拍x(套),售完这批体育用品获利y(元).
①求y与x的函数关系式,并写出x的取值范围;
②该商店实际采购时,恰逢“双十一”购物节,乒乓球拍的进价每套降低了m元(),羽毛球拍的进价不变,已知商店的售价不变,这批体育用品能够全部售完,则如何购货才能获利最大?
18.某村在政府的扶持下建起了鲜花大棚基地,准备种植,两种鲜花 经测算,种植两种鲜花每亩的投入与获利情况如下表:
每亩需投入(万元) 每亩可获利(万元)
种鲜花 2 0.8
种鲜花 4 1.2
(1)政府和村共同投入200万元全部用来种植这两种鲜花,总获利万元.设种植种鲜花亩,求关于的函数关系式;
(2)在(1)的条件下,若要求A种鲜花的种植面积不能多于B种鲜花种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.
19.某市为改善农村生活条件,满足居民清洁能源的需求,计划修建A、B两种型号的沼气池共24个,两种沼气池的修建费用、可供使用户数、占地面积如表:
沼气池 修建费用(万元/个) 可供使用户数(户/个) 占地面积(平方米/个)
A型 3 20 10
B型 2 15 8
设修建A型沼气池x个,修建两种沼气池共需费用y万元.
(1)求y与x之间的函数关系式;
(2)若此次修建沼气池至少要保证幸福村400户的居民每户一个,且政府土地部门只批给该村沼气池用地220平方米,求出费用最少时的修建方案,并计算此时修建完沼气池剩余的用地面积.
答案
一、单选题:
1.C
【分析】根据A套餐的收费为月租加上话费,B套餐的收费为话费列式,再根据两种收费相同列出方程,求解即可.
【详解】A套餐的收费方式:y1=0.1x+15;
B套餐的收费方式:y2=0.15x;
由0.1x+15=0.15x,得到x=300,
故选C.
2.A
【详解】根据总利润=单个利润×生产的个数,即可求解.
【解答】解:由题意得:y=(18﹣12﹣1)x+(12﹣8﹣0.6)(200﹣x)=1.6x+680,
故y与x之间的函数关系式为:y=1.6x+680,
故选:A.
3.B
【分析】先求出直线AB的解析式,当时,可求得一次购买6千克这种葡萄的钱数,当购买量不多于2千克时,每2千克葡萄的价格为38元,求差即可求解.
【详解】设直线AB的解析式为,
将(2,38)、(4,70)代入得,,
解得:,
当时,,
即萌萌一次购买6千克这种葡萄需要元;
她分三次购买每次购2千克这种葡萄需要(元),
∴(元),
萌萌一次购买6千克这种葡萄比她分三次购买每次购2千克这种葡萄可节省12元.
故选:B.
4.B
【分析】设该公司在这一时期内销售获得的利润是W元,销售A型电脑x台,则销售B型电脑台,根据在同一时期内,A型电脑的销售量不小于B型电脑销售量的4倍可得:,而,由一次函数性质可得答案.
【详解】解:设该公司在这一时期内销售获得的利润是W元,销售A型电脑x台,则销售B型电脑台,
根据题意得:,
解得:,
∵,,
∴随的增大而减小,
∴当时,W取最大值,最大值为(元),
答:该公司在这一时期内销售这两种电脑能获得的最大利润是46200元.
故选:B.
5.B
【分析】根据一次函数的图象,哪个函数图象在上面,哪个就大,直接得出答案即可.
【详解】解:利用图象,当游泳次数大于10次时,
在上面,即>,
∴当游泳次数为30次时,选择乙种方式省钱.
故选:B.
6.D
【分析】根据图象知道:在通话170分钟收费一样,在通话120时A收费30元,B收费50元,其中A超过120分钟后每分钟加收0.4元,B超过200分钟加收每分钟0.4元,由此即可确定有几个正确.
【详解】解:依题意得
A:(1)当0≤x≤120,yA=30,
(2)当x>120,yA=30+(x-120)×[(50-30)÷(170-120)]=0.4x-18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70-50)÷(250-200)](x-200)=0.4x-30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x-18,∴x=195,
B:60=0.4x-30,∴x=225,故(3)正确;
当A方案与B方案的费用相等,通话时间为170分钟,故(4)正确;
故选:D.
7.D
【分析】先由图1求出y与x的函数解析式,再由图2求出x与w的函数解析式,然后把w=20代入即可.
【详解】解:由图1可设y与x的函数解析式为y=kx+b,
把(92,1400)和(98,2000)代入得,
解得:,
∴y与x的函数解析式为:y=100x﹣7800;
由图2可设x与w的函数解析式为x=mw+n,
把(18,98)和(24,92)代入得:
解得:
∴x与w的函数解析式为:x=﹣w+116,
当w=20时,x=﹣20+116=96,
y=100×96﹣7800=9600﹣7800=1800(件),
∴本星期该滑板车的销量为1800件,
故选:D.
二、填空题:
8.y=48x+20(x>2)/y=20+48x(x>2)
【分析】根据已知表示出买x件礼盒的总钱数以及优惠后价格,进而得出等式即可.
【详解】解:∵凡在该商店一次性购物超过 100元者,超过100元的部分按8折优惠,李明到该商场一次性购买单价为60元的礼盒x(x>2)件,
∴李明应付货款y(元)与礼盒件数x(件)的函数关系式是:
y=(60x-100)×0.8+100=48x+20(x>2),
故答案为:y=48x+20(x>2).
9.6600
【分析】根据图象求出线段AB的解析式,求出当x=8时的y值,再根据利润公式计算即可.
【详解】解:设线段AB的解析式为y=kx+b,点A、B的坐标代入,得
,解得,
∴y=-600x+7000,
当x=8时,y=,
∴这天销售苹果的盈利是=6600(元),
故答案为:6600.
10.3520
【分析】若只租甲种客车需要辆.若只租乙种客车需要8辆,但有一辆不能坐满.只租甲种客车正好坐满,这种方式一定最贵.因而两种客车用共租8辆.两种客车的载客量大于360,根据这个不等关系,就可以求出两种客车各自的数量,进而求出租金.
【详解】解:若只租甲种客车需要辆.若只租乙种客车需要8辆,因而两种客车用共租8辆.
设甲车有x辆,乙车有辆,则,
解得:,
整数解为1、2、3、4.
设汽车的租金为,
则:,即,
的值随的增大而减小,因而当时,最小.
故取,的最小值是3520元.
11. 400 22800
【分析】设A包装的数量为x包,B包装数量为y包,总售价为W元,根据题意列出y与x的关系和W与x的函数关系式,利用一次函数的性质求解即可.
【详解】解:设A包装的数量为x包,B包装数量为y包,总售价为W元,
根据题意,得:,
∴y=-4x+2000,
由x≥-4x+2000得:x≥400,
∴W=45x+12y=45x+12(-4x+2000)=-3x+24000,
∵-3<0,
∴W随x的增大而减小,
∴当x=400时,W最大,最大为-3×400+24000=22800(元),
故答案为:400,22800.
12.70
【分析】根据表格可以求出y与x的关系式,将代入求出x的值,进一步计算即可.
【详解】设买入价x与利润y之间的函数关系式为:,
将,代入得:
,
解得:,
故:,
当代入得:
,
解得:,
即:1吨水的买入价为7元,
则买入10吨水共需元.
故答案为:70.
13.30
【分析】根据题意可设AB段的解析式为,OC段的解析式为,再结合图象利用待定系数法求出解析式,最后根据该手工作坊某一天既不盈利也不亏损时,即,可列出关于x的等式,解出x即可.
【详解】根据题意可设AB段的解析式为:,且经过点A(0,240),B(60,480),
∴ ,
解得:,
∴AB段的解析式为:;
设OC段的解析式为:,且经过点C(60,720),
∴,
解得:,
∴OC段的解析式为:.
当该手工作坊某一天既不盈利也不亏损时,即,
∴,
解得:.
所以这天的产量是30千克.
故答案为:30.
三、解答题:
14.(1)解:设甲种树苗的单价是元,则乙种树苗的单价是元,
根据题意得:,
解得:,
∴,
答:甲种树苗的单价是2元,则乙种树苗的单价是4元;
(2)解:设购买甲种树苗棵,则购买乙种树苗棵,其中为正整数,根据题意得:
,
解得:,
设总费用为元,
∴,
整理得,
∵,
∴随的增大而减小,
∴当时,最小,最小值为334,
答:最低费用是334元.
15.(1)由题意得:;
,
与之间的函数关系式为,与之间的函数关系式为;
(2)当时,,
解得,
购买种奖品超过180个时,方案二支付费用少;
当时,,
解得,
购买种奖品180个时,方案一和方案二支付费用一样多;
当时,,
解得,
购买种奖品少于180个时,方案一支付费用少.
16.(1)解:设乙工程队每天修路千米,则甲工程队每天修路千米,
由题意,得:,
解得:,
经检验,是原方程的解,
;
答:甲工程队每天修路千米,乙工程队每天修路千米;
(2)解:设甲工程队修路天,由题意,得∶
,解得:,
∵为整数,
∴可以取:;
∴共有13种方案;
设共需花费万元,由题意,得:
,
∵,随着的增大而增大,
∴当时,的值最小,
即:甲单独干10天,剩下的乙单独修完,最省钱.
答:共有13种方案,其中甲单独干10天,剩下的乙单独修完,最省钱.
17.(1)根据题意:,
解得,
答:a的值为35,b的值为40;
(2)①由题意得:
,
∵购进乒乓球拍的套数不超过150套,
∴,
∵购进乒乓球拍套数不少于羽毛球拍套数的一半,
∴,
解得:,
则x的取值范围为:,
∴y与x的函数关系式为,x的取值范围为:;
②由题意得:,
∵,
∴当即时,y随x的增大而减小,
∴当时,y有最大值,
∴乒乓球拍购进100套,羽毛球拍购进200套能获利最大;
当时,即时,y随x的增大而增大,
∴当时,y有最大值,
当时,无论购多少套,只要满足,利润都是,
而,
∴乒乓球拍购进150套,羽毛球拍购进150套能获利最大.
18.(1)解:由题意,得
;
(2)解:由题意得,
解得,
∵,且,
∴y随x的增大而增大.
∴当时,y最大值为70,
此时B种鲜花种植面积为(亩).
∴当种植A种鲜花50亩,B种鲜花25亩时,总获利最大,最大总获利为70万元.
19.解:(1)y=3x+2(24-x)=x+48,
∴y与x之间的函数关系式为.
(2)由题可得: ,
由①得:,
由②得:,
∴,
∵,其中y随x的增大而增大;
∴当时y最小,
此时,
因此方案为修建A、B两种型号的沼气池分别为8个、16个时总费用最少;
用地面积剩余:(平方米),
答:费用最少时的修建方案为修建A、B两种型号的沼气池分别为8个、16个,此时修建完沼气池剩余的用地面积为12平方米.
一、单选题:
1.某公司手机话费收费有 套餐(月租费 元,通话费每分钟 元)和 套餐(月租费 元,通话费每分钟 元)两种.当月通话时间为( )时,, 两种套餐收费一样.
A. 分钟 B. 分钟 C. 分钟 D. 分钟
2.网红“脏脏包”是时下最流行的一款面包,“脏脏包”正如其名,它看起来脏脏的,吃完以后嘴巴和手上会因沾上巧克力而变“脏”,因而得名“脏脏包”.某面包店每天固定制作甲、乙两种款型的脏脏包共200个,且所有脏脏包当天全部售出,原料成本、销售单价及店员生产提成如表所示:
甲(元/个) 乙(元/个)
原料成本 12 8
销售单价 18 12
生产提成 1 0.6
设该店每天制作甲款型的脏脏包x(个),每天获得的总利润为y(元).则y与x之间的函数关系式为( )
A.y=1.6x+680 B.y=﹣1.6x+680
C.y=﹣1.6x﹣680 D.y=﹣1.6x﹣6800
3.水果店购买一种葡萄所付款金额(元)与购买量(千克)情况如图,萌萌一次购买6千克这种葡萄比她分三次购买每次购2千克这种葡萄可节省( )元.
A.18 B.12 C.9 D.6
4.某电脑公司经营A,B两种台式电脑,分析过去的销售记录可以知道:每台A型电脑可盈利200元,每台B型电脑可盈利300元;在同一时期内,A型电脑的销售量不小于B型电脑销售量的4倍.已知该公司在同一时期内销售这两种电脑共210台,则该公司在这一时期内销售这两种电脑能获得的最大利润是( )
A.42000元 B.46200元 C.52500元 D.63000元
5.某游泳馆新推出了甲、乙两种消费卡,设游泳次数为时两种消费卡所需费用分别为,元,,与的函数图象如图所示,当游泳次数为30次时选择哪种消费卡更合算( )
A.甲种更合算 B.乙种更合算 C.两种一样合算 D.无法确定
6.如图,某电信公司提供了,两种方案的移动通讯费用(元)与通话时间(分)之间的关系,则以下说法正确的是( )
①若通话时间少于120分,则方案比方案便宜
②若通话时间超过200分,则方案比方案便宜
③通讯费用为60元,则方案比方案的通话时间多
④当通话时间是170分钟/时,两种方案通讯费用相等
A.1个 B.2个 C.3个 D.4个
7.某商场销售一种儿童滑板车,经市场调查,售价x(单位:元)、每星期销量y(单位:件)、单件利润w(单位:元)之间的关系如图1、图2所示.若某星期该滑板车单件利润为20元,则本星期该滑板车的销量为( )
A.94 B.96 C.1600 D.1800
二、填空题:
8.元旦期间,大兴商场搞优惠活动,其活动内容是:凡在本商场一次性购买商品超过100元者,超过100元的部分按8折优惠.在此活动中,小明到该商场一次性购买单价为60元的礼盒()件,则应付款(元)与商品数(件)之间的关系式,化简后的结果是______.
9.某苹果种植合作社通过网络销售苹果,图中线段为苹果日销售量(千克)与苹果售价(元)的函数图像的一部分.已知1千克苹果的成本价为5元,如果某天以8元/千克的价格销售苹果,那么这天销售苹果的盈利是_____元.
10.假期学校组织360名师生外出旅游,某客车出租公司有两种大客车可供选择:甲种客车每辆车有40个座,租金400元;乙种客车每辆车有50个座,租金480元.则租用该公司客车最少需用租金__ 元.
11.某公司生产一种营养品,每日购进所需食材500千克,制成A,B两种包装的营养品,并恰好全部用完.信息如下表:
规格 每包食材含量 每包售价
A包装 1千克 45元
B包装 0.25千克 12元
已知生产的营养品当日全部售出.若A包装的数量不少于B包装的数量,则A为__________包时,每日所获总售价最大,最大总售价为__________元.
12.某饮料厂生产一种饮料,经测算,用1吨水生产的饮料所获利润y(元)与1吨水的买入价x(元)的关系如下表:
1吨水的买入价x(元) 2 4 6 8 10
利润y(元) 202 200 198 196 194
当1吨水生产的饮料所获的利润为197元时,买入10吨水共需______元.
13.某手工作坊生产并销售某种食品,假设销售量与产量相等,如图中的线段AB、OC分别表示每天生产成本(单位:元)、收入(单位:元)与产量x(单位:千克)之间的函数关系.若该手工作坊某一天既不盈利也不亏损,则这天的产量是______千克.
三、解答题:
14.乡村振兴作为“十四五”期间的重要战略,受到了广大人民群众的关注.党的二十大再次对全面推进乡村振兴进行部署.为了发展乡村特色产业,百花村花费3000元集中采购了甲种树苗700株,乙种树苗400株,已知乙种树苗单价是甲种树苗单价的2倍.
(1)求甲、乙两种树苗的单价分别是多少元?
(2)百花村决定再购买同样的两种树苗100株用于补充栽种.其中甲种树苗不多于33株,在单价不变,总费用不超过340元的情况下,最低费用是多少元?
15.为弘扬爱国精神,传承民族文化,某校组织了“诗词里的中国”主题比赛,计划去某超市购买A,B两种奖品共300个,A种奖品每个20元,B种奖品每个15元,该超市对同时购买这两种奖品的顾客有两种销售方案(只能选择其中一种).
方案一:A种奖品每个打九折,B种奖品每个打六折.
方案二:A,B两种奖品均打八折.
设购买A种奖品x个,选择方案一的购买费用为元,选择方案二的购买费用为元.
(1)请分别写出、与x之间的函数关系式.
(2)请你计算该校选择哪种方案支付的费用较少.
16.某地计划修建一条长36千米的乡村公路,已知甲工程队修路的速度是乙工程队修路速度的倍,乙工程队单独完成本次修路任务比甲工程队单独完成多20天.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)已知甲工程队修路费用为25万元/千米,乙工程队修路费用为20万元/千米.甲工程队先单独修路若干天后,接到其它任务需要离开,剩下的工程由乙工程队单独完成.若要使修路总时间不超过55天,总费用不超过820万元,且甲工程队所修路程需为整数,请问共有几种修路方案?哪种方案最省钱?
17.“双减”政策颁布后,各校重视了延迟服务,并在延迟服务中加大了体育活动的力度.某体育用品商店抓住商机,计划购进300套乒乓球拍和羽毛球拍进行销售,其中购进乒乓球拍的套数不超过150套,它们的进价和售价如下表:
进价 售价
乒乓球拍(元/套) a 50
羽毛球拍(元/套) b 60
已知购进2套乒乓球拍和1套羽毛球拍需花费110元,购进4套乒乓球拍和3套羽毛球拍需花费260元.
(1)求出a,b的值;
(2)该面店根据以往销售经验,决定购进乒乓球拍套数不少于羽毛球拍套数的一半,设购进乒乓球拍x(套),售完这批体育用品获利y(元).
①求y与x的函数关系式,并写出x的取值范围;
②该商店实际采购时,恰逢“双十一”购物节,乒乓球拍的进价每套降低了m元(),羽毛球拍的进价不变,已知商店的售价不变,这批体育用品能够全部售完,则如何购货才能获利最大?
18.某村在政府的扶持下建起了鲜花大棚基地,准备种植,两种鲜花 经测算,种植两种鲜花每亩的投入与获利情况如下表:
每亩需投入(万元) 每亩可获利(万元)
种鲜花 2 0.8
种鲜花 4 1.2
(1)政府和村共同投入200万元全部用来种植这两种鲜花,总获利万元.设种植种鲜花亩,求关于的函数关系式;
(2)在(1)的条件下,若要求A种鲜花的种植面积不能多于B种鲜花种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.
19.某市为改善农村生活条件,满足居民清洁能源的需求,计划修建A、B两种型号的沼气池共24个,两种沼气池的修建费用、可供使用户数、占地面积如表:
沼气池 修建费用(万元/个) 可供使用户数(户/个) 占地面积(平方米/个)
A型 3 20 10
B型 2 15 8
设修建A型沼气池x个,修建两种沼气池共需费用y万元.
(1)求y与x之间的函数关系式;
(2)若此次修建沼气池至少要保证幸福村400户的居民每户一个,且政府土地部门只批给该村沼气池用地220平方米,求出费用最少时的修建方案,并计算此时修建完沼气池剩余的用地面积.
答案
一、单选题:
1.C
【分析】根据A套餐的收费为月租加上话费,B套餐的收费为话费列式,再根据两种收费相同列出方程,求解即可.
【详解】A套餐的收费方式:y1=0.1x+15;
B套餐的收费方式:y2=0.15x;
由0.1x+15=0.15x,得到x=300,
故选C.
2.A
【详解】根据总利润=单个利润×生产的个数,即可求解.
【解答】解:由题意得:y=(18﹣12﹣1)x+(12﹣8﹣0.6)(200﹣x)=1.6x+680,
故y与x之间的函数关系式为:y=1.6x+680,
故选:A.
3.B
【分析】先求出直线AB的解析式,当时,可求得一次购买6千克这种葡萄的钱数,当购买量不多于2千克时,每2千克葡萄的价格为38元,求差即可求解.
【详解】设直线AB的解析式为,
将(2,38)、(4,70)代入得,,
解得:,
当时,,
即萌萌一次购买6千克这种葡萄需要元;
她分三次购买每次购2千克这种葡萄需要(元),
∴(元),
萌萌一次购买6千克这种葡萄比她分三次购买每次购2千克这种葡萄可节省12元.
故选:B.
4.B
【分析】设该公司在这一时期内销售获得的利润是W元,销售A型电脑x台,则销售B型电脑台,根据在同一时期内,A型电脑的销售量不小于B型电脑销售量的4倍可得:,而,由一次函数性质可得答案.
【详解】解:设该公司在这一时期内销售获得的利润是W元,销售A型电脑x台,则销售B型电脑台,
根据题意得:,
解得:,
∵,,
∴随的增大而减小,
∴当时,W取最大值,最大值为(元),
答:该公司在这一时期内销售这两种电脑能获得的最大利润是46200元.
故选:B.
5.B
【分析】根据一次函数的图象,哪个函数图象在上面,哪个就大,直接得出答案即可.
【详解】解:利用图象,当游泳次数大于10次时,
在上面,即>,
∴当游泳次数为30次时,选择乙种方式省钱.
故选:B.
6.D
【分析】根据图象知道:在通话170分钟收费一样,在通话120时A收费30元,B收费50元,其中A超过120分钟后每分钟加收0.4元,B超过200分钟加收每分钟0.4元,由此即可确定有几个正确.
【详解】解:依题意得
A:(1)当0≤x≤120,yA=30,
(2)当x>120,yA=30+(x-120)×[(50-30)÷(170-120)]=0.4x-18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70-50)÷(250-200)](x-200)=0.4x-30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x-18,∴x=195,
B:60=0.4x-30,∴x=225,故(3)正确;
当A方案与B方案的费用相等,通话时间为170分钟,故(4)正确;
故选:D.
7.D
【分析】先由图1求出y与x的函数解析式,再由图2求出x与w的函数解析式,然后把w=20代入即可.
【详解】解:由图1可设y与x的函数解析式为y=kx+b,
把(92,1400)和(98,2000)代入得,
解得:,
∴y与x的函数解析式为:y=100x﹣7800;
由图2可设x与w的函数解析式为x=mw+n,
把(18,98)和(24,92)代入得:
解得:
∴x与w的函数解析式为:x=﹣w+116,
当w=20时,x=﹣20+116=96,
y=100×96﹣7800=9600﹣7800=1800(件),
∴本星期该滑板车的销量为1800件,
故选:D.
二、填空题:
8.y=48x+20(x>2)/y=20+48x(x>2)
【分析】根据已知表示出买x件礼盒的总钱数以及优惠后价格,进而得出等式即可.
【详解】解:∵凡在该商店一次性购物超过 100元者,超过100元的部分按8折优惠,李明到该商场一次性购买单价为60元的礼盒x(x>2)件,
∴李明应付货款y(元)与礼盒件数x(件)的函数关系式是:
y=(60x-100)×0.8+100=48x+20(x>2),
故答案为:y=48x+20(x>2).
9.6600
【分析】根据图象求出线段AB的解析式,求出当x=8时的y值,再根据利润公式计算即可.
【详解】解:设线段AB的解析式为y=kx+b,点A、B的坐标代入,得
,解得,
∴y=-600x+7000,
当x=8时,y=,
∴这天销售苹果的盈利是=6600(元),
故答案为:6600.
10.3520
【分析】若只租甲种客车需要辆.若只租乙种客车需要8辆,但有一辆不能坐满.只租甲种客车正好坐满,这种方式一定最贵.因而两种客车用共租8辆.两种客车的载客量大于360,根据这个不等关系,就可以求出两种客车各自的数量,进而求出租金.
【详解】解:若只租甲种客车需要辆.若只租乙种客车需要8辆,因而两种客车用共租8辆.
设甲车有x辆,乙车有辆,则,
解得:,
整数解为1、2、3、4.
设汽车的租金为,
则:,即,
的值随的增大而减小,因而当时,最小.
故取,的最小值是3520元.
11. 400 22800
【分析】设A包装的数量为x包,B包装数量为y包,总售价为W元,根据题意列出y与x的关系和W与x的函数关系式,利用一次函数的性质求解即可.
【详解】解:设A包装的数量为x包,B包装数量为y包,总售价为W元,
根据题意,得:,
∴y=-4x+2000,
由x≥-4x+2000得:x≥400,
∴W=45x+12y=45x+12(-4x+2000)=-3x+24000,
∵-3<0,
∴W随x的增大而减小,
∴当x=400时,W最大,最大为-3×400+24000=22800(元),
故答案为:400,22800.
12.70
【分析】根据表格可以求出y与x的关系式,将代入求出x的值,进一步计算即可.
【详解】设买入价x与利润y之间的函数关系式为:,
将,代入得:
,
解得:,
故:,
当代入得:
,
解得:,
即:1吨水的买入价为7元,
则买入10吨水共需元.
故答案为:70.
13.30
【分析】根据题意可设AB段的解析式为,OC段的解析式为,再结合图象利用待定系数法求出解析式,最后根据该手工作坊某一天既不盈利也不亏损时,即,可列出关于x的等式,解出x即可.
【详解】根据题意可设AB段的解析式为:,且经过点A(0,240),B(60,480),
∴ ,
解得:,
∴AB段的解析式为:;
设OC段的解析式为:,且经过点C(60,720),
∴,
解得:,
∴OC段的解析式为:.
当该手工作坊某一天既不盈利也不亏损时,即,
∴,
解得:.
所以这天的产量是30千克.
故答案为:30.
三、解答题:
14.(1)解:设甲种树苗的单价是元,则乙种树苗的单价是元,
根据题意得:,
解得:,
∴,
答:甲种树苗的单价是2元,则乙种树苗的单价是4元;
(2)解:设购买甲种树苗棵,则购买乙种树苗棵,其中为正整数,根据题意得:
,
解得:,
设总费用为元,
∴,
整理得,
∵,
∴随的增大而减小,
∴当时,最小,最小值为334,
答:最低费用是334元.
15.(1)由题意得:;
,
与之间的函数关系式为,与之间的函数关系式为;
(2)当时,,
解得,
购买种奖品超过180个时,方案二支付费用少;
当时,,
解得,
购买种奖品180个时,方案一和方案二支付费用一样多;
当时,,
解得,
购买种奖品少于180个时,方案一支付费用少.
16.(1)解:设乙工程队每天修路千米,则甲工程队每天修路千米,
由题意,得:,
解得:,
经检验,是原方程的解,
;
答:甲工程队每天修路千米,乙工程队每天修路千米;
(2)解:设甲工程队修路天,由题意,得∶
,解得:,
∵为整数,
∴可以取:;
∴共有13种方案;
设共需花费万元,由题意,得:
,
∵,随着的增大而增大,
∴当时,的值最小,
即:甲单独干10天,剩下的乙单独修完,最省钱.
答:共有13种方案,其中甲单独干10天,剩下的乙单独修完,最省钱.
17.(1)根据题意:,
解得,
答:a的值为35,b的值为40;
(2)①由题意得:
,
∵购进乒乓球拍的套数不超过150套,
∴,
∵购进乒乓球拍套数不少于羽毛球拍套数的一半,
∴,
解得:,
则x的取值范围为:,
∴y与x的函数关系式为,x的取值范围为:;
②由题意得:,
∵,
∴当即时,y随x的增大而减小,
∴当时,y有最大值,
∴乒乓球拍购进100套,羽毛球拍购进200套能获利最大;
当时,即时,y随x的增大而增大,
∴当时,y有最大值,
当时,无论购多少套,只要满足,利润都是,
而,
∴乒乓球拍购进150套,羽毛球拍购进150套能获利最大.
18.(1)解:由题意,得
;
(2)解:由题意得,
解得,
∵,且,
∴y随x的增大而增大.
∴当时,y最大值为70,
此时B种鲜花种植面积为(亩).
∴当种植A种鲜花50亩,B种鲜花25亩时,总获利最大,最大总获利为70万元.
19.解:(1)y=3x+2(24-x)=x+48,
∴y与x之间的函数关系式为.
(2)由题可得: ,
由①得:,
由②得:,
∴,
∵,其中y随x的增大而增大;
∴当时y最小,
此时,
因此方案为修建A、B两种型号的沼气池分别为8个、16个时总费用最少;
用地面积剩余:(平方米),
答:费用最少时的修建方案为修建A、B两种型号的沼气池分别为8个、16个,此时修建完沼气池剩余的用地面积为12平方米.
