人教版六年级下册数学反比例 课件(共38张PPT)
文档属性
| 名称 | 人教版六年级下册数学反比例 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-01 00:00:00 | ||
图片预览









文档简介
(共38张PPT)
反比例
六
下
数
学
1
2
3
4
温故知新
新知探究
课堂练习
课堂小结
目
录
CONTENTS
温故知新
学而时习之,不亦说乎。
03
1
正比例关系的意义是什么?
复习
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比的比值一定,这两种量就叫做成正比例的量,它们之间的关系叫做正比例关系。
判断两种相关联量成不成正比例的关键是什么?
比值一定
(1)工作效率一定,工作时间和工作总量。
(2)每头奶牛的产奶量一定,奶牛的头数和产奶总量。
(3)正方形的边长和它的面积。
判断下面各题中的两种量是否成正比例?为什么?
面包总价与数量之间有什么关系呢?为什么?
同样的面包单价为2元。
数量/个
总价/元
1
2
2
4
3
6
4
8
5
10
6
14
7
12
8
16
…
…
正比例关系
两种相关联的量的比值(商)一定。
新知探究
学,然后知不足。
03
2
面包店有以下单价的面包,小明有30元,可以买同种面包多少个。请填写表格。
单价/元
数量/个
1
30
2
15
3
10
5
6
10
3
…
…
通过表格,你发现了什么?
单价增加,购买的数量随着减少。
总价不变。
单价和数量成正比例吗?
那是什么关系呢?
体积/cm
60
30
20
15
10
底面积/cm
5
10
15
20
30
高度/cm
3
2
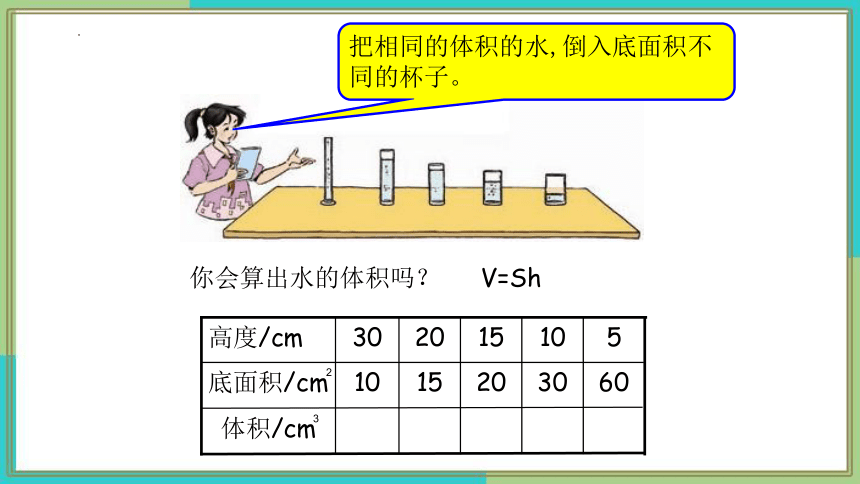
把相同的体积的水,倒入底面积不同的杯子。
你会算出水的体积吗?
V=Sh
(1)表中有哪几个量?
(2)水中的高度是怎样随着杯子底面积的大小变化而变换的?
(3)相对应的底面积与水的高度的成积分别是多少?
300
300
300
300
300
体积/cm
60
30
20
15
10
底面积/cm
5
10
15
20
30
高度/cm
3
2
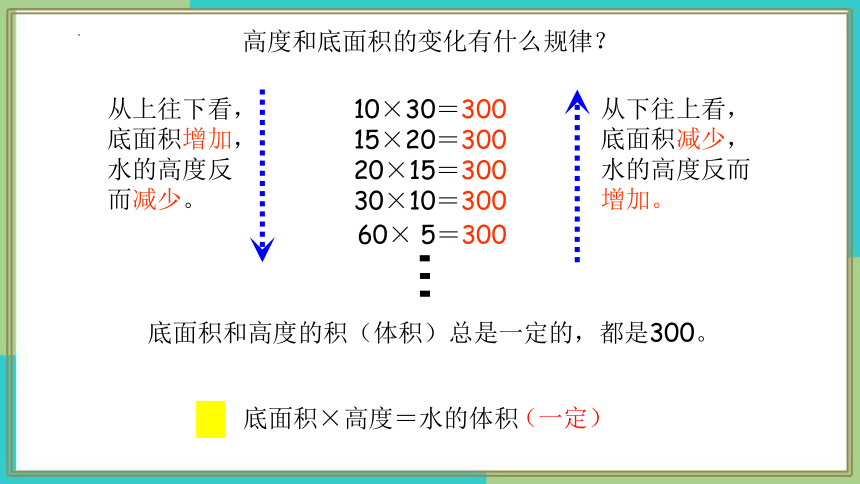
底面积和高度的积(体积)总是一定的,都是300。
10×30=300
15×20=300
20×15=300
30×10=300
60× 5=300
从上往下看,底面积增加,水的高度反而减少。
从下往上看,底面积减少,水的高度反而增加。
(一定)
底面积×高度=水的体积
高度和底面积的变化有什么规律?
(1)水的高度和底面积是相关联的量。
(2)水的体积一定,水的高度随着底面积的变化而变化;底面积增加,高度反而降低,底面积减少,高度反而升高。
(3)水的高度和底面积的积是一定的。
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
底面积×水的高度=水的体积(一定)
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用下面的式子表示:
x×y=k(一定)
判定方法
判定两个量是不是成反比例,主要是看它们的积是不是一定的。
两种量成反比例关系要满足以下三个条件:
(1)必须是两种相关联的量。
(2)一种量变化,另一种量也随着变化。
(3)两种量中相对应的两个数的积一定。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。 XY=K(一定)
(一定)
速度×时间=路程
每杯的果汁量× 分的杯数= 果汁总量(一定)
有600毫升果汁,可平均分成若干杯。请把下表填完整
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
15
200
300
(1)表中有哪两种量?
(2)分的杯数是怎样随着每杯的果汁量变化的
(3)它们的关系是什么?
(3)每杯的果汁量和分的杯数的积是一定的。
每杯的果汁量× 分的杯数= 果汁总量(一定)
有600毫升果汁,可平均分成若干杯。请把下表填完整
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
15
200
300
(1)表中有每杯的果汁量和分的杯数两种量。
(2)每杯的果汁量扩大,分的杯数反而缩小;
每杯的果汁量缩小,分的杯数反而扩大;
想一想:生活中还有哪两种量成反比例关系?
排队做操,总人数不变,排队的行数和每行的人数成反比例;
煤的总吨数一定,每天烧的吨数和烧的天数成反比例;
买东西,总钱数一定,它的单价和数量成反比例;
……
你知道吗?
生产天数
0
100
200
300
400
500
600
吨/天
10
20
30
40
50
60
反比例关系也可以
用图象表示。如前面研
究的每天生产啤酒的吨
数和生产天数的关系可
以表示为右图。
在加法表上把和是12的方格圈起来,可连成一条直线。
12 13 14 15 16 17 18 19 20 21 22 23 24
11 12 13 14 15 16 17 18 19 20 21 22 23
10 11 12 13 14 15 16 17 18 19 20 21 22
9 10 11 12 13 14 15 16 17 18 19 20 21
8 9 10 11 12 13 14 15 16 17 18 19 20
7 8 9 10 11 12 13 14 15 16 17 18 19
6 7 8 9 10 11 12 13 14 15 16 17 18
5 6 7 8 9 10 11 12 13 14 15 16 17
4 5 6 7 8 9 10 11 12 13 14 15 16
3 4 5 6 7 8 9 10 11 12 13 14 15
2 3 4 5 6 7 8 9 10 11 12 13 14
1 2 3 4 5 6 7 8 9 10 11 12 13
+ 1 2 3 4 5 6 7 8 9 10 11 12
3+9=12
在乘法表上把积是12的方格圈起来,可连成一条曲线。
12 12 24 36 48 60 72 84 96 108 120 132 144
11 11 22 33 44 55 66 77 88 99 110 121 132
10 10 20 30 40 50 60 70 80 90 100 110 120
9 19 18 27 36 45 54 63 72 81 90 99 108
8 8 16 24 32 40 48 56 64 72 80 88 96
7 7 14 21 28 35 42 49 56 63 70 77 84
6 6 12 18 24 30 36 42 48 54 60 66 72
5 5 10 15 20 25 30 35 40 45 50 55 60
4 4 8 12 16 20 24 28 32 36 40 44 48
3 3 6 9 12 15 18 21 24 27 30 33 36
2 2 4 6 8 10 12 14 16 18 20 22 24
1 1 2 3 4 5 6 7 8 9 10 11 12
+ 1 2 3 4 5 6 7 8 9 10 11 12
3×4=12
想一想,成反比例的两个量的图像会怎样呢?
课堂练习
纸上得来终觉浅,绝知此事要躬行。
03
3
判断下面每题中的两种量是不是成反比例,并说明理由。
煤的总量一定,每天的烧煤量和能够烧的天数。
张伯伯骑自行车从家到县城,骑自行车的速度和所需的时间。
判断下面每题中的两种量是不是成反比例,并说明理由。
生产电视机的总台数一定,每天生产的台数和所用的天数。
判断下面每题中的两种量是不是成反比例,并说明理由。
长方形的面积一定,它的长和宽。
判断下面每题中的两种量是不是成反比例,并说明理由。
铺地面积一定,方砖边长与所需块数。
判断下面每题中的两种量是不是成反比例,并说明理由。
A.正比例 B.反比例 C.不成比例
1.小明的身高和体重。( )
2.圆锥的体积一定,底面积和高。( )
3.正方体的表面积和其中一个面的面积。( )
4.所行路程一定,车轮周长和车轮转数。( )
5.甲数是乙数的4/5,那么甲数与乙数。( )
6.长方形的周长一定,长与宽。( )
我有一双火眼金睛
C
B
A
B
A
C
两种量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
→不成比例
→不成比例
→不成比例
积一定
商一定
→成反比例
→成正比例
比例分正反,关键在判断。
三种量分清,关系式列全。
定商是正比,反比积一定。
关系非乘除,比例它无关。
判断下面每题中的两种量是不是成反比例,并说明理由。
⑴行驶的路程一定,车轮的周长与车轮需要转动的圈数。
⑵一个人跑步的速度和他的体重。
⑶平行四边形的面积一定,它的底和高。
⑷笑笑从家步行到学校,已走的路程和剩下的路程。
积一定,周长和转动圈数成反比例。
跑步速度与体重不成比例。
积一定,底和高成反比例。
和一定,它们不成比例。
行驶路程=车轮周长×转动圈数
跑步速度与体重没有必然关系
平行四边形面积=底×高
全程=已走路程+剩下路程
平均每天看的页数 10 15 20 30 40
看完全书所需天数 12
把下表补充完整。
6
8
4
3
平均每天看的页数越多,看完全书所需天数就越少。
平均每天看的页数和看完全书所需天数的积一定,都是120页,每天看的页数和所需天数成反比例。
10×12=120
15×8=120
20×6=120
30×4=120
40×3=120
课堂小结
学而不思则惘,思而不学则殆。
03
4
1.两个相关联的量,一个变化另一个也随着变化,而且它们的积一定,我们就说这两个量成反比例。
2.判断两个量是否成反比例,关健是看它们的积是否一定。
这节课你们都学会了哪些知识?
课堂小结
反比例
两种相关联的量,一种量变化,另一种量也随着变化,且两种量的乘积一定。
y
x
=k
(一定)
知识小结
欢迎
Welcome
好久不见
你 好
HELLO
认识你很开心
谢谢观看
反比例
六
下
数
学
1
2
3
4
温故知新
新知探究
课堂练习
课堂小结
目
录
CONTENTS
温故知新
学而时习之,不亦说乎。
03
1
正比例关系的意义是什么?
复习
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比的比值一定,这两种量就叫做成正比例的量,它们之间的关系叫做正比例关系。
判断两种相关联量成不成正比例的关键是什么?
比值一定
(1)工作效率一定,工作时间和工作总量。
(2)每头奶牛的产奶量一定,奶牛的头数和产奶总量。
(3)正方形的边长和它的面积。
判断下面各题中的两种量是否成正比例?为什么?
面包总价与数量之间有什么关系呢?为什么?
同样的面包单价为2元。
数量/个
总价/元
1
2
2
4
3
6
4
8
5
10
6
14
7
12
8
16
…
…
正比例关系
两种相关联的量的比值(商)一定。
新知探究
学,然后知不足。
03
2
面包店有以下单价的面包,小明有30元,可以买同种面包多少个。请填写表格。
单价/元
数量/个
1
30
2
15
3
10
5
6
10
3
…
…
通过表格,你发现了什么?
单价增加,购买的数量随着减少。
总价不变。
单价和数量成正比例吗?
那是什么关系呢?
体积/cm
60
30
20
15
10
底面积/cm
5
10
15
20
30
高度/cm
3
2
把相同的体积的水,倒入底面积不同的杯子。
你会算出水的体积吗?
V=Sh
(1)表中有哪几个量?
(2)水中的高度是怎样随着杯子底面积的大小变化而变换的?
(3)相对应的底面积与水的高度的成积分别是多少?
300
300
300
300
300
体积/cm
60
30
20
15
10
底面积/cm
5
10
15
20
30
高度/cm
3
2
底面积和高度的积(体积)总是一定的,都是300。
10×30=300
15×20=300
20×15=300
30×10=300
60× 5=300
从上往下看,底面积增加,水的高度反而减少。
从下往上看,底面积减少,水的高度反而增加。
(一定)
底面积×高度=水的体积
高度和底面积的变化有什么规律?
(1)水的高度和底面积是相关联的量。
(2)水的体积一定,水的高度随着底面积的变化而变化;底面积增加,高度反而降低,底面积减少,高度反而升高。
(3)水的高度和底面积的积是一定的。
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
底面积×水的高度=水的体积(一定)
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用下面的式子表示:
x×y=k(一定)
判定方法
判定两个量是不是成反比例,主要是看它们的积是不是一定的。
两种量成反比例关系要满足以下三个条件:
(1)必须是两种相关联的量。
(2)一种量变化,另一种量也随着变化。
(3)两种量中相对应的两个数的积一定。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。 XY=K(一定)
(一定)
速度×时间=路程
每杯的果汁量× 分的杯数= 果汁总量(一定)
有600毫升果汁,可平均分成若干杯。请把下表填完整
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
15
200
300
(1)表中有哪两种量?
(2)分的杯数是怎样随着每杯的果汁量变化的
(3)它们的关系是什么?
(3)每杯的果汁量和分的杯数的积是一定的。
每杯的果汁量× 分的杯数= 果汁总量(一定)
有600毫升果汁,可平均分成若干杯。请把下表填完整
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
15
200
300
(1)表中有每杯的果汁量和分的杯数两种量。
(2)每杯的果汁量扩大,分的杯数反而缩小;
每杯的果汁量缩小,分的杯数反而扩大;
想一想:生活中还有哪两种量成反比例关系?
排队做操,总人数不变,排队的行数和每行的人数成反比例;
煤的总吨数一定,每天烧的吨数和烧的天数成反比例;
买东西,总钱数一定,它的单价和数量成反比例;
……
你知道吗?
生产天数
0
100
200
300
400
500
600
吨/天
10
20
30
40
50
60
反比例关系也可以
用图象表示。如前面研
究的每天生产啤酒的吨
数和生产天数的关系可
以表示为右图。
在加法表上把和是12的方格圈起来,可连成一条直线。
12 13 14 15 16 17 18 19 20 21 22 23 24
11 12 13 14 15 16 17 18 19 20 21 22 23
10 11 12 13 14 15 16 17 18 19 20 21 22
9 10 11 12 13 14 15 16 17 18 19 20 21
8 9 10 11 12 13 14 15 16 17 18 19 20
7 8 9 10 11 12 13 14 15 16 17 18 19
6 7 8 9 10 11 12 13 14 15 16 17 18
5 6 7 8 9 10 11 12 13 14 15 16 17
4 5 6 7 8 9 10 11 12 13 14 15 16
3 4 5 6 7 8 9 10 11 12 13 14 15
2 3 4 5 6 7 8 9 10 11 12 13 14
1 2 3 4 5 6 7 8 9 10 11 12 13
+ 1 2 3 4 5 6 7 8 9 10 11 12
3+9=12
在乘法表上把积是12的方格圈起来,可连成一条曲线。
12 12 24 36 48 60 72 84 96 108 120 132 144
11 11 22 33 44 55 66 77 88 99 110 121 132
10 10 20 30 40 50 60 70 80 90 100 110 120
9 19 18 27 36 45 54 63 72 81 90 99 108
8 8 16 24 32 40 48 56 64 72 80 88 96
7 7 14 21 28 35 42 49 56 63 70 77 84
6 6 12 18 24 30 36 42 48 54 60 66 72
5 5 10 15 20 25 30 35 40 45 50 55 60
4 4 8 12 16 20 24 28 32 36 40 44 48
3 3 6 9 12 15 18 21 24 27 30 33 36
2 2 4 6 8 10 12 14 16 18 20 22 24
1 1 2 3 4 5 6 7 8 9 10 11 12
+ 1 2 3 4 5 6 7 8 9 10 11 12
3×4=12
想一想,成反比例的两个量的图像会怎样呢?
课堂练习
纸上得来终觉浅,绝知此事要躬行。
03
3
判断下面每题中的两种量是不是成反比例,并说明理由。
煤的总量一定,每天的烧煤量和能够烧的天数。
张伯伯骑自行车从家到县城,骑自行车的速度和所需的时间。
判断下面每题中的两种量是不是成反比例,并说明理由。
生产电视机的总台数一定,每天生产的台数和所用的天数。
判断下面每题中的两种量是不是成反比例,并说明理由。
长方形的面积一定,它的长和宽。
判断下面每题中的两种量是不是成反比例,并说明理由。
铺地面积一定,方砖边长与所需块数。
判断下面每题中的两种量是不是成反比例,并说明理由。
A.正比例 B.反比例 C.不成比例
1.小明的身高和体重。( )
2.圆锥的体积一定,底面积和高。( )
3.正方体的表面积和其中一个面的面积。( )
4.所行路程一定,车轮周长和车轮转数。( )
5.甲数是乙数的4/5,那么甲数与乙数。( )
6.长方形的周长一定,长与宽。( )
我有一双火眼金睛
C
B
A
B
A
C
两种量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
→不成比例
→不成比例
→不成比例
积一定
商一定
→成反比例
→成正比例
比例分正反,关键在判断。
三种量分清,关系式列全。
定商是正比,反比积一定。
关系非乘除,比例它无关。
判断下面每题中的两种量是不是成反比例,并说明理由。
⑴行驶的路程一定,车轮的周长与车轮需要转动的圈数。
⑵一个人跑步的速度和他的体重。
⑶平行四边形的面积一定,它的底和高。
⑷笑笑从家步行到学校,已走的路程和剩下的路程。
积一定,周长和转动圈数成反比例。
跑步速度与体重不成比例。
积一定,底和高成反比例。
和一定,它们不成比例。
行驶路程=车轮周长×转动圈数
跑步速度与体重没有必然关系
平行四边形面积=底×高
全程=已走路程+剩下路程
平均每天看的页数 10 15 20 30 40
看完全书所需天数 12
把下表补充完整。
6
8
4
3
平均每天看的页数越多,看完全书所需天数就越少。
平均每天看的页数和看完全书所需天数的积一定,都是120页,每天看的页数和所需天数成反比例。
10×12=120
15×8=120
20×6=120
30×4=120
40×3=120
课堂小结
学而不思则惘,思而不学则殆。
03
4
1.两个相关联的量,一个变化另一个也随着变化,而且它们的积一定,我们就说这两个量成反比例。
2.判断两个量是否成反比例,关健是看它们的积是否一定。
这节课你们都学会了哪些知识?
课堂小结
反比例
两种相关联的量,一种量变化,另一种量也随着变化,且两种量的乘积一定。
y
x
=k
(一定)
知识小结
欢迎
Welcome
好久不见
你 好
HELLO
认识你很开心
谢谢观看
