高中数学人教必修四课件142正余弦函数的性质两课时(共25张PPT)
文档属性
| 名称 | 高中数学人教必修四课件142正余弦函数的性质两课时(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 456.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-26 00:00:00 | ||
图片预览



文档简介
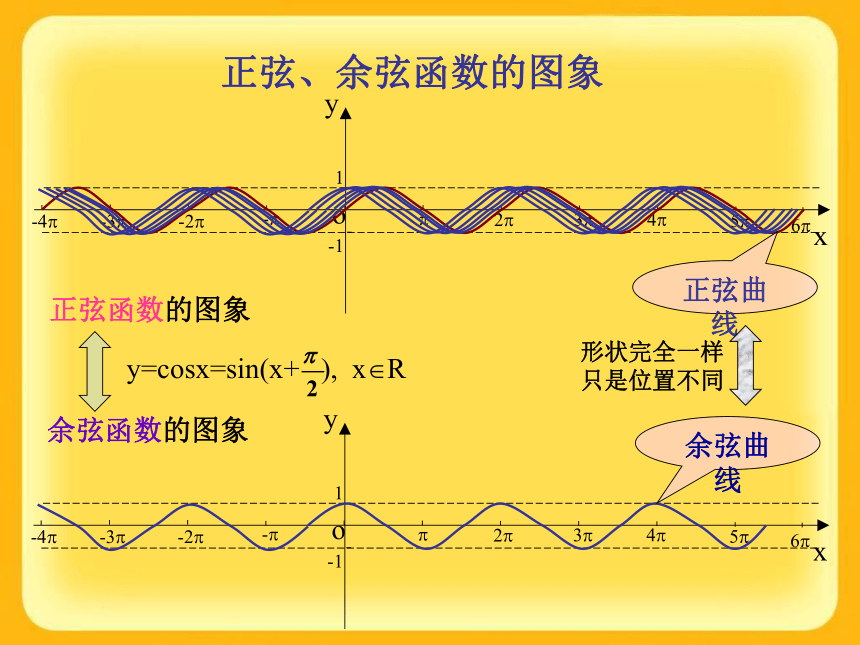
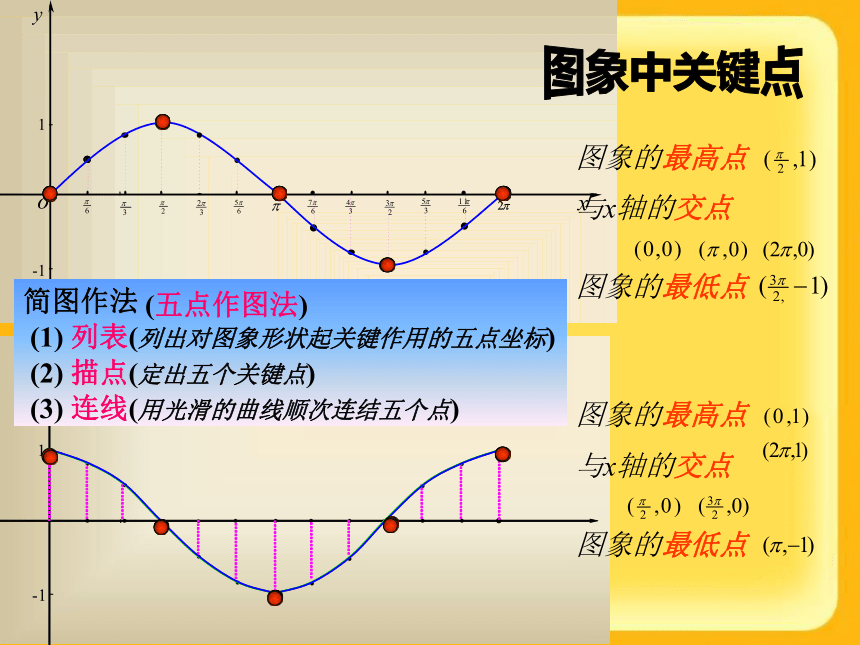
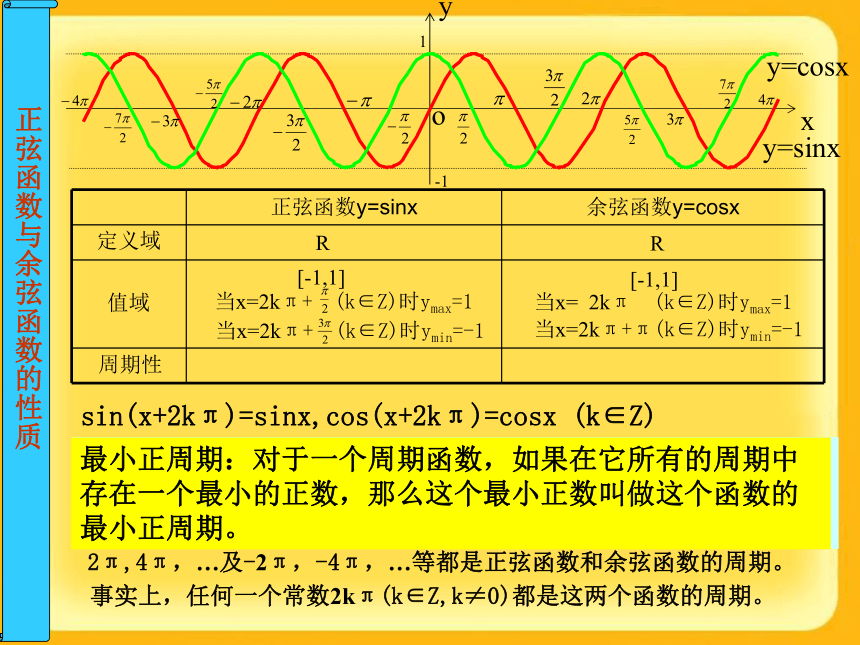
课件25张PPT。1.4.2 正弦函数、余弦函数的性质第一课时 正弦、余弦函数的图象 余弦函数的图象 正弦函数的图象 y=cosx=sin(x+ ), x?R余弦曲线正弦曲线形状完全一样只是位置不同与x轴的交点图象的最高点图象的最低点与x轴的交点图象的最高点图象的最低点图象中关键点简图作法
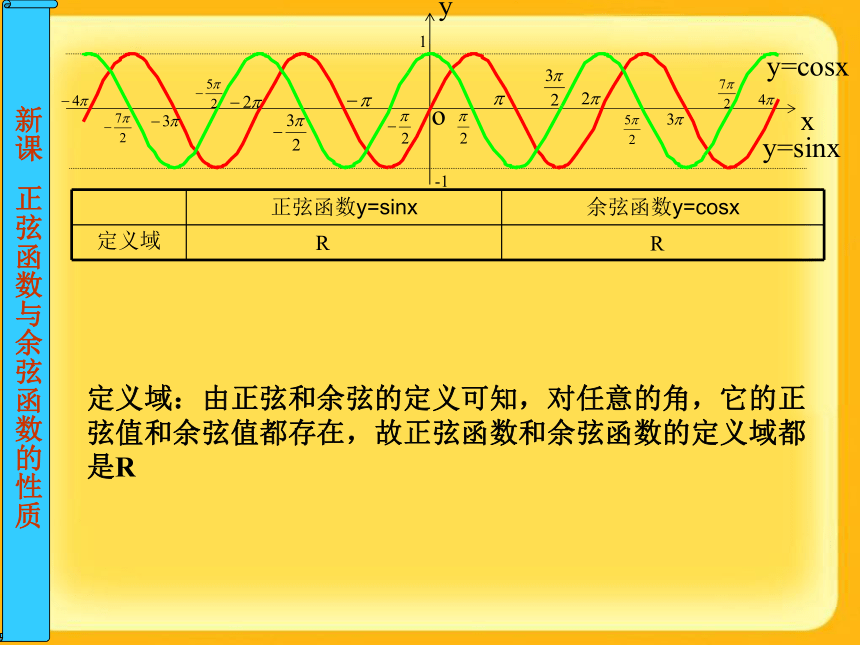
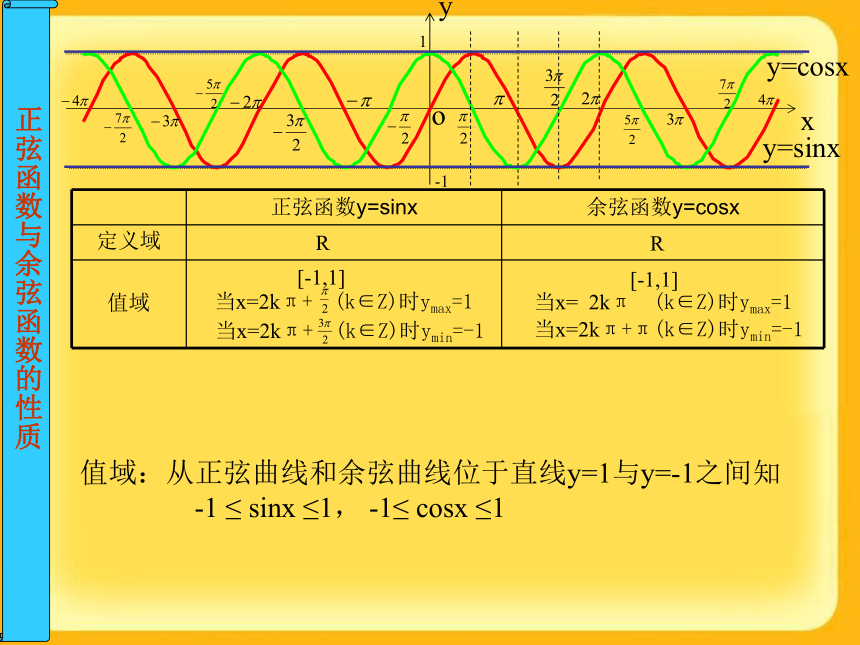
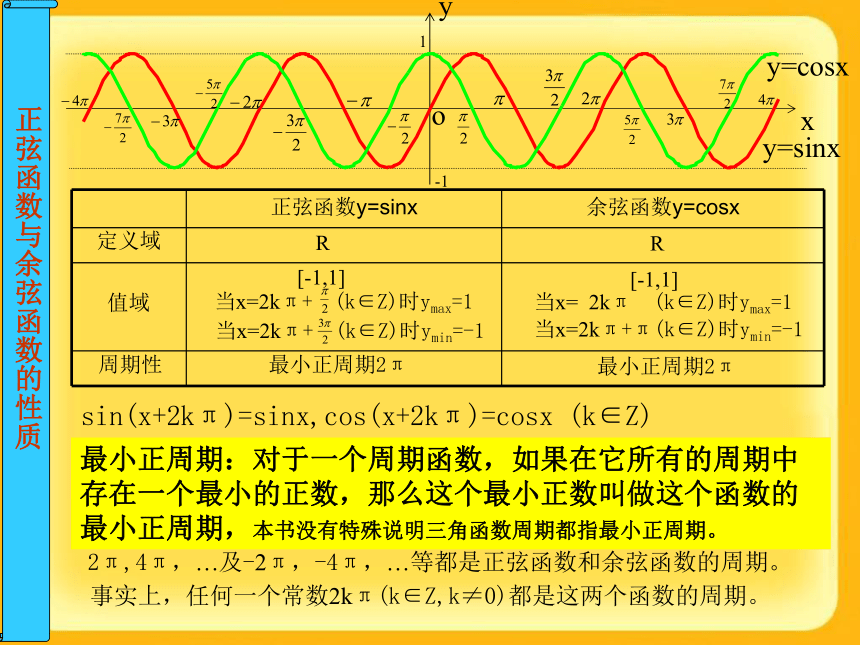
(五点作图法)(1) 列表(列出对图象形状起关键作用的五点坐标)(2) 描点(定出五个关键点)(3) 连线(用光滑的曲线顺次连结五个点)RR定义域定义域:由正弦和余弦的定义可知,对任意的角,它的正弦值和余弦值都存在,故正弦函数和余弦函数的定义域都是RRR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1定义域值域值域:从正弦曲线和余弦曲线位于直线y=1与y=-1之间知 -1 ≤ sinx ≤1, -1≤ cosx ≤1正弦、余弦函数的定义域和值域 例2 写出下列函数的定义域、值域RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1定义域值域周期性周期函数:对于函数f(x),如果存在一个非零的常数T,使得当x取定义域内的每一个值,都有f(x+T)=f(x),那么函数f(x)叫做周期函数,非零常数T叫做这个函数的周期。sin(x+2kπ)=sinx,cos(x+2kπ)=cosx (k∈Z)2π,4π,…及-2π,-4π,…等都是正弦函数和余弦函数的周期。事实上,任何一个常数2kπ(k∈Z,k≠0)都是这两个函数的周期。最小正周期:对于一个周期函数,如果在它所有的周期中存在一个最小的正数,那么这个最小正数叫做这个函数的最小正周期。RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1定义域值域周期性sin(x+2kπ)=sinx,cos(x+2kπ)=cosx (k∈Z)2π,4π,…及-2π,-4π,…等都是正弦函数和余弦函数的周期。事实上,任何一个常数2kπ(k∈Z,k≠0)都是这两个函数的周期。最小正周期2π最小正周期2π最小正周期:对于一个周期函数,如果在它所有的周期中存在一个最小的正数,那么这个最小正数叫做这个函数的最小正周期,本书没有特殊说明三角函数周期都指最小正周期。正弦、余弦函数的周期周期公式: 正弦、余弦函数的周期练习:教材36页第2题最小正周期2π最小正周期2π 小结RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1定义域值域周期性 思考题
已知定义在R上的函数f(x)满足下列关系:
f(x+2)=-f(x)
试判断f(x)是否为周期函数?1.4.2 正弦函数、余弦函数的性质第二课时函数奇偶性的概念:奇函数定义:
如果对于f(x)定义域内的任意一个x,都有f(-x)=-f(x) ,
那么函数f(x)就叫奇函数. 偶函数定义:
如果对于f(x)定义域内的任意一个x,都有f(-x)=f(x), 那么函数f(x)就叫偶函数.复习回顾☆对奇函数、偶函数定义的说明:(1).函数具有奇偶性的前提是:定义域关于原点对称。 (2) 若f(x)为奇函数, 则f(-x)=-f(x)成立。
若f(x)为偶函数, 则f(-x)= f(x) 成立。(3) 如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x) 具有奇偶性。复习回顾奇偶函数图象的性质: ⑴ 奇函数的图象关于原点对称.
反过来,如果一个函数的图象关于原点对称,
那么这个函数为奇函数.⑵ 偶函数的图象关于y轴对称.反过来,如果一个函数的图象关于y轴对称,那么这个函数为偶函数.注:奇偶函数图象的性质可用于:
①.判断函数的奇偶性。
②.简化函数图象的画法。复习回顾RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1最小正周期2π最小正周期2π奇函数偶函数定义域值域周期性奇偶性奇偶性:由诱导公式sin(-x)=-sinx,cos(-x)=cosx知,正弦函数是奇函数,余弦函数是偶函数。从图象看正弦函数图象关于原点对称,余弦函数关于y轴对称,也能确定函数的奇偶性。例1.判断下列函数的奇偶性:正弦、余弦函数的奇偶性RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1最小正周期2π最小正周期2π奇函数偶函数定义域值域周期性奇偶性单调性RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1最小正周期2π最小正周期2π奇函数偶函数定义域值域周期性奇偶性单调性正弦、余弦函数的单调性例2.利用三角函数的单调性,比较下列各组数的大小:分析:先用诱导公式化到同一单调区间内正弦、余弦函数的单调性分析:复合函数的换元法RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1最小正周期2π最小正周期2π奇函数偶函数定义域值域周期性奇偶性单调性说明:最大值与最小值合称为最值正弦、余弦函数的最值例4.下列函数有最大值、最小值么?如果有,请写出取最大值、最小值时的自变量x的集合,并说出最大值、最小值分别是什么?RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1最小正周期2π最小正周期2π奇函数偶函数定义域值域周期性奇偶性单调性 小结思考:教材39页“ ?”思考题
(五点作图法)(1) 列表(列出对图象形状起关键作用的五点坐标)(2) 描点(定出五个关键点)(3) 连线(用光滑的曲线顺次连结五个点)RR定义域定义域:由正弦和余弦的定义可知,对任意的角,它的正弦值和余弦值都存在,故正弦函数和余弦函数的定义域都是RRR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1定义域值域值域:从正弦曲线和余弦曲线位于直线y=1与y=-1之间知 -1 ≤ sinx ≤1, -1≤ cosx ≤1正弦、余弦函数的定义域和值域 例2 写出下列函数的定义域、值域RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1定义域值域周期性周期函数:对于函数f(x),如果存在一个非零的常数T,使得当x取定义域内的每一个值,都有f(x+T)=f(x),那么函数f(x)叫做周期函数,非零常数T叫做这个函数的周期。sin(x+2kπ)=sinx,cos(x+2kπ)=cosx (k∈Z)2π,4π,…及-2π,-4π,…等都是正弦函数和余弦函数的周期。事实上,任何一个常数2kπ(k∈Z,k≠0)都是这两个函数的周期。最小正周期:对于一个周期函数,如果在它所有的周期中存在一个最小的正数,那么这个最小正数叫做这个函数的最小正周期。RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1定义域值域周期性sin(x+2kπ)=sinx,cos(x+2kπ)=cosx (k∈Z)2π,4π,…及-2π,-4π,…等都是正弦函数和余弦函数的周期。事实上,任何一个常数2kπ(k∈Z,k≠0)都是这两个函数的周期。最小正周期2π最小正周期2π最小正周期:对于一个周期函数,如果在它所有的周期中存在一个最小的正数,那么这个最小正数叫做这个函数的最小正周期,本书没有特殊说明三角函数周期都指最小正周期。正弦、余弦函数的周期周期公式: 正弦、余弦函数的周期练习:教材36页第2题最小正周期2π最小正周期2π 小结RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1定义域值域周期性 思考题
已知定义在R上的函数f(x)满足下列关系:
f(x+2)=-f(x)
试判断f(x)是否为周期函数?1.4.2 正弦函数、余弦函数的性质第二课时函数奇偶性的概念:奇函数定义:
如果对于f(x)定义域内的任意一个x,都有f(-x)=-f(x) ,
那么函数f(x)就叫奇函数. 偶函数定义:
如果对于f(x)定义域内的任意一个x,都有f(-x)=f(x), 那么函数f(x)就叫偶函数.复习回顾☆对奇函数、偶函数定义的说明:(1).函数具有奇偶性的前提是:定义域关于原点对称。 (2) 若f(x)为奇函数, 则f(-x)=-f(x)成立。
若f(x)为偶函数, 则f(-x)= f(x) 成立。(3) 如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x) 具有奇偶性。复习回顾奇偶函数图象的性质: ⑴ 奇函数的图象关于原点对称.
反过来,如果一个函数的图象关于原点对称,
那么这个函数为奇函数.⑵ 偶函数的图象关于y轴对称.反过来,如果一个函数的图象关于y轴对称,那么这个函数为偶函数.注:奇偶函数图象的性质可用于:
①.判断函数的奇偶性。
②.简化函数图象的画法。复习回顾RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1最小正周期2π最小正周期2π奇函数偶函数定义域值域周期性奇偶性奇偶性:由诱导公式sin(-x)=-sinx,cos(-x)=cosx知,正弦函数是奇函数,余弦函数是偶函数。从图象看正弦函数图象关于原点对称,余弦函数关于y轴对称,也能确定函数的奇偶性。例1.判断下列函数的奇偶性:正弦、余弦函数的奇偶性RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1最小正周期2π最小正周期2π奇函数偶函数定义域值域周期性奇偶性单调性RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1最小正周期2π最小正周期2π奇函数偶函数定义域值域周期性奇偶性单调性正弦、余弦函数的单调性例2.利用三角函数的单调性,比较下列各组数的大小:分析:先用诱导公式化到同一单调区间内正弦、余弦函数的单调性分析:复合函数的换元法RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1最小正周期2π最小正周期2π奇函数偶函数定义域值域周期性奇偶性单调性说明:最大值与最小值合称为最值正弦、余弦函数的最值例4.下列函数有最大值、最小值么?如果有,请写出取最大值、最小值时的自变量x的集合,并说出最大值、最小值分别是什么?RR[-1,1][-1,1]当x=2kπ+ (k∈Z)时ymax=1当x=2kπ+ (k∈Z)时ymin=-1当x= 2kπ (k∈Z)时ymax=1当x=2kπ+π(k∈Z)时ymin=-1最小正周期2π最小正周期2π奇函数偶函数定义域值域周期性奇偶性单调性 小结思考:教材39页“ ?”思考题
