20.2数据的集中趋势与离散程度 同步练习(含答案)
文档属性
| 名称 | 20.2数据的集中趋势与离散程度 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 296.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-04 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
20.2数据的集中趋势与离散程度
一、单选题
1.小芳应聘广告策划时进行了三项素质测试,其中创新能力、综合知识和语言表达的成绩分别为分,分,分,分别按的比例计入总成绩,则小芳的总成绩是( )
A.分 B.分 C.分 D.分
2.已知样本的数据如下:,,,,,,,样本的数据恰好是样本数据每个都加,则,两个样本的下列统计量对应相同的是( ).
A.方差 B.平均数 C.中位数 D.众数
3.如表记录了甲、乙、丙、丁四名学生近10次英语词汇成绩的数据信息,要选择一名成绩好又发挥稳定的学生参加年级英语词汇比赛,应该选择的是( )
甲 乙 丙 丁
平均数(分) 90 93 93 92
方差() 1.5 8.5 1.5 5.5
A.甲 B.乙 C.丙 D.丁
4.为落实“双减”政策,学校随机调查了部分学生一周平均每天的睡眠时间,统计结果如表,则这些被调查学生睡眠时间的众数和中位数分别是( )
时间小时 7 8 9 10
人数 7 9 11 3
A.9,8 B.9,9 C.11,8 D.11,8.5
5.一组数据4,2, ,3,9的平均数为4,则这组数据的众数和中位数分别是( )
A.2,2 B.2,3 C.3,2 D.2,4
二、填空题
6.已知一组数据 的众数为3,平均数为 ,则n的值为 .
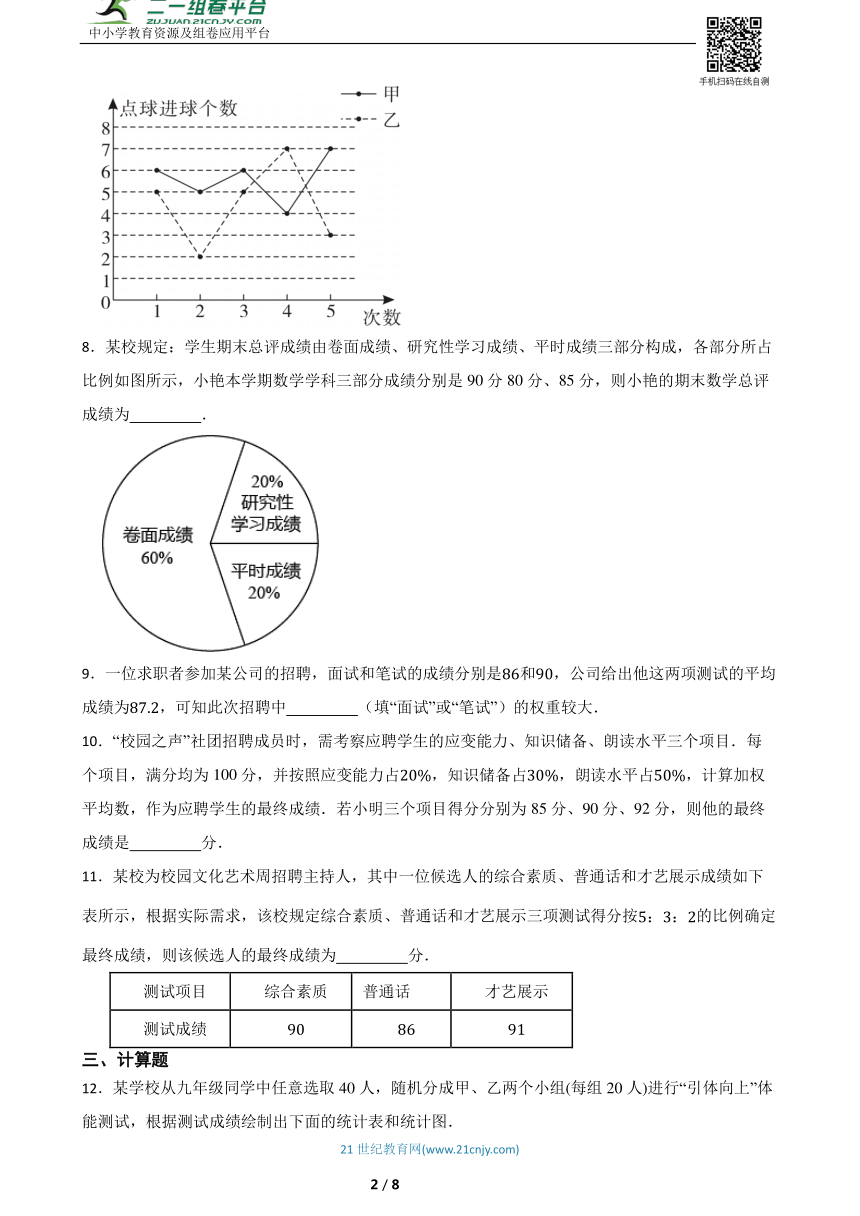
7.如图是甲、乙两人次足球点球测试每次点球个成绩的统计图,甲、乙两人测试成绩的方差分别记作、,则 填“”“”或“”.
8.某校规定:学生期末总评成绩由卷面成绩、研究性学习成绩、平时成绩三部分构成,各部分所占比例如图所示,小艳本学期数学学科三部分成绩分别是90分80分、85分,则小艳的期末数学总评成绩为 .
9.一位求职者参加某公司的招聘,面试和笔试的成绩分别是和,公司给出他这两项测试的平均成绩为,可知此次招聘中 (填“面试”或“笔试”)的权重较大.
10.“校园之声”社团招聘成员时,需考察应聘学生的应变能力、知识储备、朗读水平三个项目.每个项目,满分均为100分,并按照应变能力占,知识储备占,朗读水平占,计算加权平均数,作为应聘学生的最终成绩.若小明三个项目得分分别为85分、90分、92分,则他的最终成绩是 分.
11.某校为校园文化艺术周招聘主持人,其中一位候选人的综合素质、普通话和才艺展示成绩如下表所示,根据实际需求,该校规定综合素质、普通话和才艺展示三项测试得分按的比例确定最终成绩,则该候选人的最终成绩为 分.
测试项目 综合素质 普通话 才艺展示
测试成绩
三、计算题
12.某学校从九年级同学中任意选取40人,随机分成甲、乙两个小组(每组20人)进行“引体向上”体能测试,根据测试成绩绘制出下面的统计表和统计图.
甲组成绩统计表
成绩 7 8 9 10
人数 1 9 5 5
乙组成绩统计图
请根据上面的信息,解答下列问题:
(1)甲组成绩的中位数是 ,乙组成绩的众数是 ;
(2)请求出乙组成绩的平均数;
(3)已知甲组成绩的方差为,请求乙组成绩的方差,并判断哪个小组的成绩更加稳定.
四、解答题
13.(某学校准备在新的学期举办“篮球特色班”,大量热爱篮球的同学踊跃报名,但需要考核选拔,考核成绩由篮球知识、身体素质、篮球技能三项构成,已知甲同学这三项成绩分别为93分、94分、89分,且根据实际需要,将三项成绩按如图所示的权重确定考核成绩,请计算出甲同学的考核成绩.
五、作图题
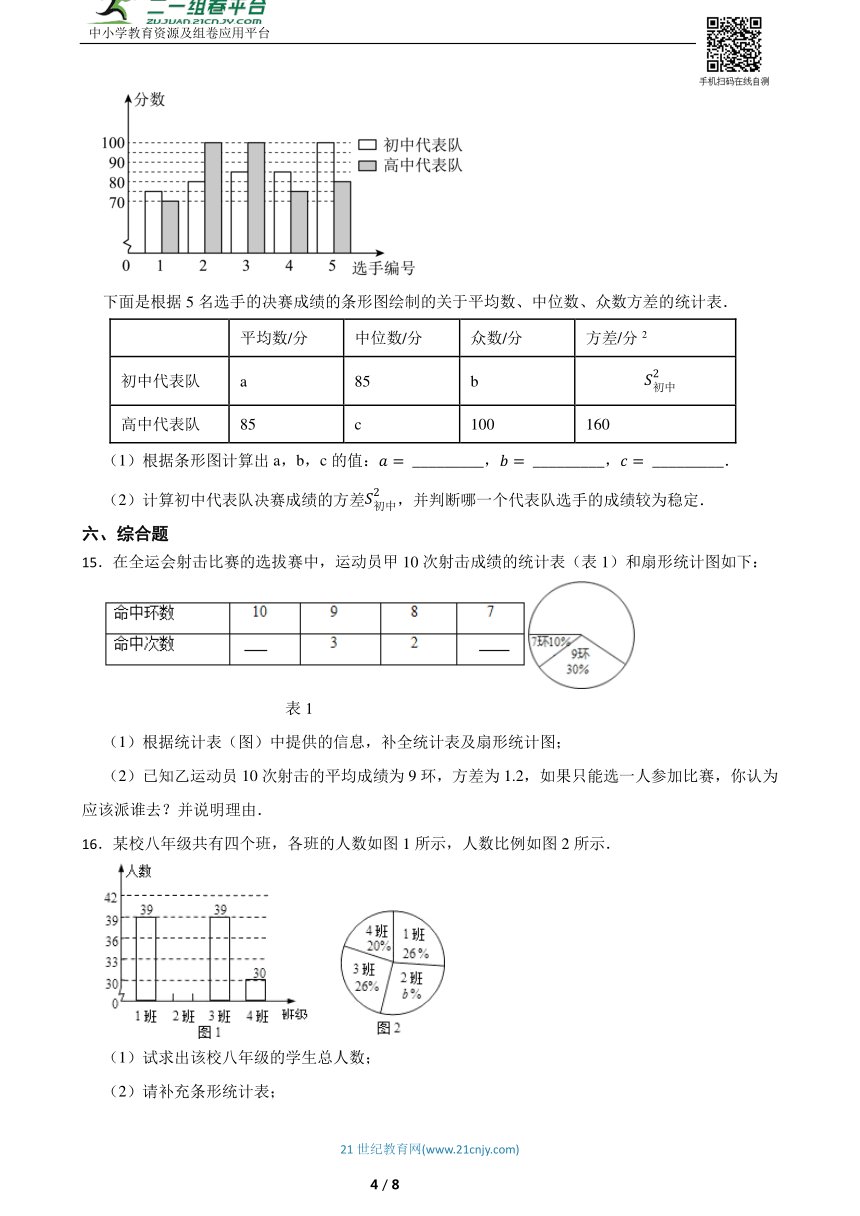
14.某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如条形图所示.
下面是根据5名选手的决赛成绩的条形图绘制的关于平均数、中位数、众数方差的统计表.
平均数/分 中位数/分 众数/分 方差/分2
初中代表队 a 85 b
高中代表队 85 c 100 160
(1)根据条形图计算出a,b,c的值: _________, _________, _________.
(2)计算初中代表队决赛成绩的方差,并判断哪一个代表队选手的成绩较为稳定.
六、综合题
15.在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表(表1)和扇形统计图如下:
表1
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.
16.某校八年级共有四个班,各班的人数如图1所示,人数比例如图2所示.
(1)试求出该校八年级的学生总人数;
(2)请补充条形统计表;
(3)在一次数学考试中,1班、2班、3班、4班的平均成绩分别为92分、91分、90分、95分.试求出该校八年级学生在本次数学考试的平均分.
17.在甲、乙两名同学中选拔一人参加“英语口语听力”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,81,82,85,83 乙:88,79,90,81,72.
(1)求甲、乙两名同学测试成绩的方差;
(2)请你选择一个角度来判断选拔谁参加比赛更合适.
七、实践探究题
18. “防溺水”是校园安全教育工作重点之一.某校为确保学生安全,开展了“远离溺水 珍爱生命”的防溺水安全知识竞赛.现从七年级、八年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
七年级:92,75,82,96,84,90,85,97,85,92,68,100,85,86,95,85,89,90,91,93.
八年级:90,87,93,97,90,84,92,72,100,80,90,91,59,93,87,90,82,91,92,100.
【整理与分析数据】
50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100
七年级 0 1 1 8 a
八年级 1 0 1 5 13
【应用数据】
平均数 众数 中位数
七年级 88 85 b
八年级 88 c 90
(1)由上表填空:a= ,b= ,c= ;
(2)若成绩不低于90分为优秀等次,该校七、八年级共有学生1600人,请你估计两个年级在本次竞赛中获得优秀等次的共有多少人?
(3)你认为哪个年级的学生对防溺水安全知识掌握的总体水平较好,请从两个不同的角度说明理由.
答案解析部分
1.【答案】D
【知识点】加权平均数及其计算
2.【答案】A
【知识点】平均数及其计算;中位数;方差;众数
3.【答案】C
【知识点】分析数据的波动程度
4.【答案】A
【知识点】中位数;众数
5.【答案】B
【知识点】平均数及其计算;中位数;众数
6.【答案】-2
【知识点】平均数及其计算;众数
7.【答案】
【知识点】方差
8.【答案】87分
【知识点】加权平均数及其计算
9.【答案】面试
【知识点】一元一次方程的其他应用;加权平均数及其计算
10.【答案】90
【知识点】加权平均数及其计算
11.【答案】
【知识点】加权平均数及其计算
12.【答案】(1);8
(2)
(3);乙组更加稳定些
【知识点】平均数及其计算;中位数;方差;众数
13.【答案】91.3
【知识点】加权平均数及其计算
14.【答案】(1)85,85,80
(2)初中代表队选手的成绩较为稳定
【知识点】平均数及其计算;中位数;方差;众数
15.【答案】(1)解答:解:如下图所示:
(2)解答:应该派甲去.∵甲运动员10次射击的平均成绩为(10×4+9×3+8×2+7×1)÷10=9环,∴甲运动员10次射击的方差是 [(10-9)2×4+(9-9)2×3+(8-9)2×2+(7-9)2]=1,∵乙运动员10次射击的平均成绩为9环,方差为1.2,大于甲的方差,∴如果只能选一人参加比赛,认为应该派甲去.
【知识点】统计表;扇形统计图;方差
16.【答案】(1)解:∵1班有39人,占26%,
∴该校八年级的学生总人数为:39÷26%=150(人)
(2)解:2班:150﹣39﹣39﹣30=42(人);
如图:
(3)解:该校八年级学生在本次数学考试的平均分为: =91.8(分)
【知识点】扇形统计图;条形统计图;加权平均数及其计算
17.【答案】(1)解:甲平均分为 (分)
乙的平均分为 (分)
甲的方差:
乙的方差
(2)解:选拔甲参加比赛更合适,
∵4<42,甲、乙的平均分相等,
甲的方差较小
∴甲的成绩比较稳定
∴选拔甲参加比赛更合适.
【知识点】方差
18.【答案】(1)10;;90
(2)解:(人),
答:估计两个年级在本次竞赛中获得优秀等次的共有920人.
(3)解:八年级的学生对防溺水安全知识掌握的总体水平较好.
理由:七、八年级的平均分相等;八年级成绩的众数为90,高于七年级学生成绩的众数85;八年级成绩的中位数为90,高于七年级学生成绩的中位数,综合比较,八年级的学生对防溺水安全知识掌握的总体水平较好.
【知识点】频数(率)分布表;中位数;分析数据的集中趋势(平均数、中位数、众数);众数
21世纪教育网(www.21cnjy.com)
1 / 8
20.2数据的集中趋势与离散程度
一、单选题
1.小芳应聘广告策划时进行了三项素质测试,其中创新能力、综合知识和语言表达的成绩分别为分,分,分,分别按的比例计入总成绩,则小芳的总成绩是( )
A.分 B.分 C.分 D.分
2.已知样本的数据如下:,,,,,,,样本的数据恰好是样本数据每个都加,则,两个样本的下列统计量对应相同的是( ).
A.方差 B.平均数 C.中位数 D.众数
3.如表记录了甲、乙、丙、丁四名学生近10次英语词汇成绩的数据信息,要选择一名成绩好又发挥稳定的学生参加年级英语词汇比赛,应该选择的是( )
甲 乙 丙 丁
平均数(分) 90 93 93 92
方差() 1.5 8.5 1.5 5.5
A.甲 B.乙 C.丙 D.丁
4.为落实“双减”政策,学校随机调查了部分学生一周平均每天的睡眠时间,统计结果如表,则这些被调查学生睡眠时间的众数和中位数分别是( )
时间小时 7 8 9 10
人数 7 9 11 3
A.9,8 B.9,9 C.11,8 D.11,8.5
5.一组数据4,2, ,3,9的平均数为4,则这组数据的众数和中位数分别是( )
A.2,2 B.2,3 C.3,2 D.2,4
二、填空题
6.已知一组数据 的众数为3,平均数为 ,则n的值为 .
7.如图是甲、乙两人次足球点球测试每次点球个成绩的统计图,甲、乙两人测试成绩的方差分别记作、,则 填“”“”或“”.
8.某校规定:学生期末总评成绩由卷面成绩、研究性学习成绩、平时成绩三部分构成,各部分所占比例如图所示,小艳本学期数学学科三部分成绩分别是90分80分、85分,则小艳的期末数学总评成绩为 .
9.一位求职者参加某公司的招聘,面试和笔试的成绩分别是和,公司给出他这两项测试的平均成绩为,可知此次招聘中 (填“面试”或“笔试”)的权重较大.
10.“校园之声”社团招聘成员时,需考察应聘学生的应变能力、知识储备、朗读水平三个项目.每个项目,满分均为100分,并按照应变能力占,知识储备占,朗读水平占,计算加权平均数,作为应聘学生的最终成绩.若小明三个项目得分分别为85分、90分、92分,则他的最终成绩是 分.
11.某校为校园文化艺术周招聘主持人,其中一位候选人的综合素质、普通话和才艺展示成绩如下表所示,根据实际需求,该校规定综合素质、普通话和才艺展示三项测试得分按的比例确定最终成绩,则该候选人的最终成绩为 分.
测试项目 综合素质 普通话 才艺展示
测试成绩
三、计算题
12.某学校从九年级同学中任意选取40人,随机分成甲、乙两个小组(每组20人)进行“引体向上”体能测试,根据测试成绩绘制出下面的统计表和统计图.
甲组成绩统计表
成绩 7 8 9 10
人数 1 9 5 5
乙组成绩统计图
请根据上面的信息,解答下列问题:
(1)甲组成绩的中位数是 ,乙组成绩的众数是 ;
(2)请求出乙组成绩的平均数;
(3)已知甲组成绩的方差为,请求乙组成绩的方差,并判断哪个小组的成绩更加稳定.
四、解答题
13.(某学校准备在新的学期举办“篮球特色班”,大量热爱篮球的同学踊跃报名,但需要考核选拔,考核成绩由篮球知识、身体素质、篮球技能三项构成,已知甲同学这三项成绩分别为93分、94分、89分,且根据实际需要,将三项成绩按如图所示的权重确定考核成绩,请计算出甲同学的考核成绩.
五、作图题
14.某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如条形图所示.
下面是根据5名选手的决赛成绩的条形图绘制的关于平均数、中位数、众数方差的统计表.
平均数/分 中位数/分 众数/分 方差/分2
初中代表队 a 85 b
高中代表队 85 c 100 160
(1)根据条形图计算出a,b,c的值: _________, _________, _________.
(2)计算初中代表队决赛成绩的方差,并判断哪一个代表队选手的成绩较为稳定.
六、综合题
15.在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表(表1)和扇形统计图如下:
表1
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.
16.某校八年级共有四个班,各班的人数如图1所示,人数比例如图2所示.
(1)试求出该校八年级的学生总人数;
(2)请补充条形统计表;
(3)在一次数学考试中,1班、2班、3班、4班的平均成绩分别为92分、91分、90分、95分.试求出该校八年级学生在本次数学考试的平均分.
17.在甲、乙两名同学中选拔一人参加“英语口语听力”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,81,82,85,83 乙:88,79,90,81,72.
(1)求甲、乙两名同学测试成绩的方差;
(2)请你选择一个角度来判断选拔谁参加比赛更合适.
七、实践探究题
18. “防溺水”是校园安全教育工作重点之一.某校为确保学生安全,开展了“远离溺水 珍爱生命”的防溺水安全知识竞赛.现从七年级、八年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
七年级:92,75,82,96,84,90,85,97,85,92,68,100,85,86,95,85,89,90,91,93.
八年级:90,87,93,97,90,84,92,72,100,80,90,91,59,93,87,90,82,91,92,100.
【整理与分析数据】
50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100
七年级 0 1 1 8 a
八年级 1 0 1 5 13
【应用数据】
平均数 众数 中位数
七年级 88 85 b
八年级 88 c 90
(1)由上表填空:a= ,b= ,c= ;
(2)若成绩不低于90分为优秀等次,该校七、八年级共有学生1600人,请你估计两个年级在本次竞赛中获得优秀等次的共有多少人?
(3)你认为哪个年级的学生对防溺水安全知识掌握的总体水平较好,请从两个不同的角度说明理由.
答案解析部分
1.【答案】D
【知识点】加权平均数及其计算
2.【答案】A
【知识点】平均数及其计算;中位数;方差;众数
3.【答案】C
【知识点】分析数据的波动程度
4.【答案】A
【知识点】中位数;众数
5.【答案】B
【知识点】平均数及其计算;中位数;众数
6.【答案】-2
【知识点】平均数及其计算;众数
7.【答案】
【知识点】方差
8.【答案】87分
【知识点】加权平均数及其计算
9.【答案】面试
【知识点】一元一次方程的其他应用;加权平均数及其计算
10.【答案】90
【知识点】加权平均数及其计算
11.【答案】
【知识点】加权平均数及其计算
12.【答案】(1);8
(2)
(3);乙组更加稳定些
【知识点】平均数及其计算;中位数;方差;众数
13.【答案】91.3
【知识点】加权平均数及其计算
14.【答案】(1)85,85,80
(2)初中代表队选手的成绩较为稳定
【知识点】平均数及其计算;中位数;方差;众数
15.【答案】(1)解答:解:如下图所示:
(2)解答:应该派甲去.∵甲运动员10次射击的平均成绩为(10×4+9×3+8×2+7×1)÷10=9环,∴甲运动员10次射击的方差是 [(10-9)2×4+(9-9)2×3+(8-9)2×2+(7-9)2]=1,∵乙运动员10次射击的平均成绩为9环,方差为1.2,大于甲的方差,∴如果只能选一人参加比赛,认为应该派甲去.
【知识点】统计表;扇形统计图;方差
16.【答案】(1)解:∵1班有39人,占26%,
∴该校八年级的学生总人数为:39÷26%=150(人)
(2)解:2班:150﹣39﹣39﹣30=42(人);
如图:
(3)解:该校八年级学生在本次数学考试的平均分为: =91.8(分)
【知识点】扇形统计图;条形统计图;加权平均数及其计算
17.【答案】(1)解:甲平均分为 (分)
乙的平均分为 (分)
甲的方差:
乙的方差
(2)解:选拔甲参加比赛更合适,
∵4<42,甲、乙的平均分相等,
甲的方差较小
∴甲的成绩比较稳定
∴选拔甲参加比赛更合适.
【知识点】方差
18.【答案】(1)10;;90
(2)解:(人),
答:估计两个年级在本次竞赛中获得优秀等次的共有920人.
(3)解:八年级的学生对防溺水安全知识掌握的总体水平较好.
理由:七、八年级的平均分相等;八年级成绩的众数为90,高于七年级学生成绩的众数85;八年级成绩的中位数为90,高于七年级学生成绩的中位数,综合比较,八年级的学生对防溺水安全知识掌握的总体水平较好.
【知识点】频数(率)分布表;中位数;分析数据的集中趋势(平均数、中位数、众数);众数
21世纪教育网(www.21cnjy.com)
1 / 8
