人教版八年级数学下册 20.1.1 平均数 同步练习(含详解)
文档属性
| 名称 | 人教版八年级数学下册 20.1.1 平均数 同步练习(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 920.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-04 00:00:00 | ||
图片预览


文档简介
20.1.1 平均数
一、单选题:
1.某校九年级甲班40名学生中,5人13岁,30人14岁,5人15岁,则这个班级学生的平均年龄为( )
A.14岁 B.14.5岁 C.13.5岁 D.15岁
2.甲、乙、丙三种糖果的售价分别为每千克6元、7元、8元,若将甲种10千克、乙种9千克、丙种3千克混在一起出售,为确保不亏本,售价至少应定为每千克( )
A.6元 B.6.5元 C.6.7元 D.7元
3.下表中,若平均数为2,则x等于( ).
A.0 B.1 C.2 D.3
4.王老师为了了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,将获得的数据绘制成如图所示的条形图,则这10名学生周末学均时间为( )
A.1.7 B.3 C.3.3 D.3.7
5.为了了解学生参与家务劳动情况,某老师在所任教班级随机调查了10名学生一周做家务劳动的时间,其统计数据如表:
时间(单位:小时) 4 3 2 1 0
人数 2 4 2 1 1
则这10名学生一周做家务劳动的平均时间是( )小时.
A.3.5 B.3 C.2.5 D.2
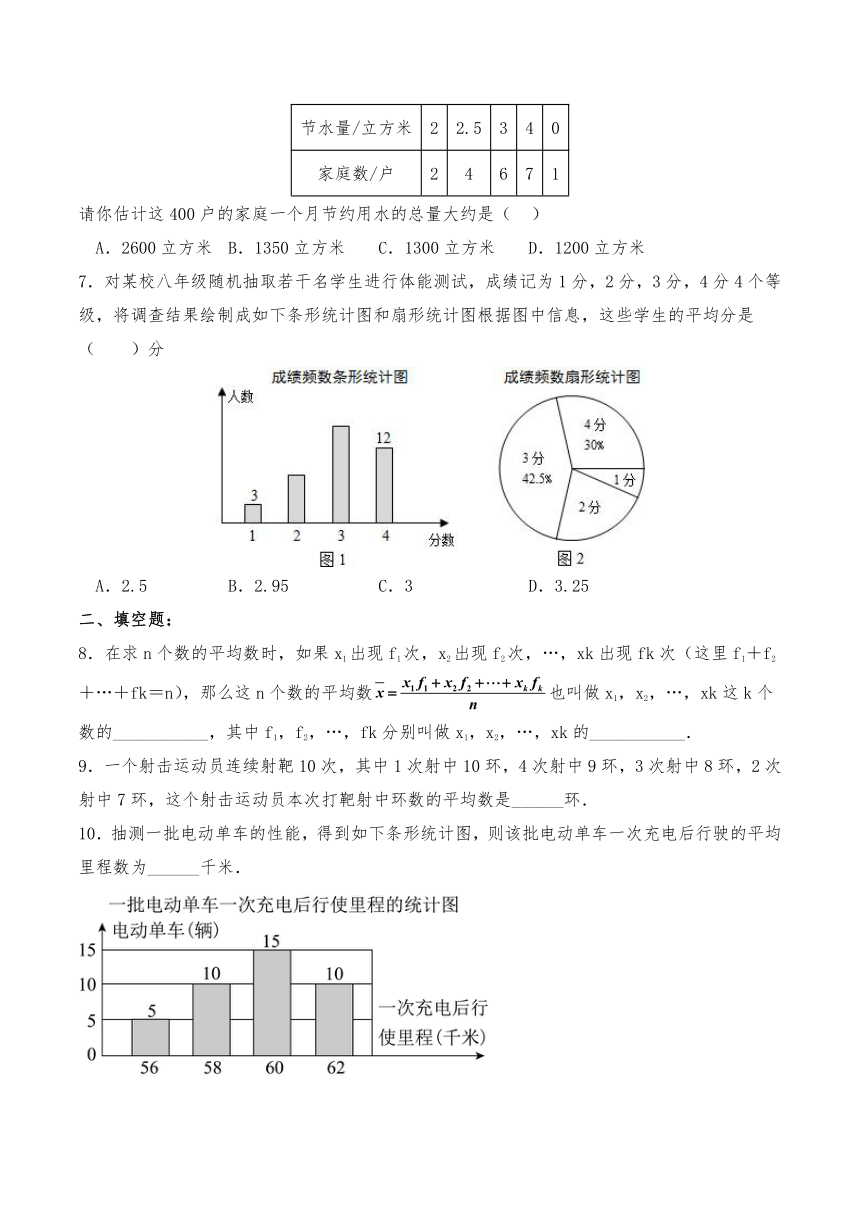
6.某小区开展节约每一滴水活动,为了了解开展活动一个月以来节约用水的情况,从400户中随机选取20户统计了各自家庭一个月节约用水情况.表格如下:
节水量/立方米 2 2.5 3 4 0
家庭数/户 2 4 6 7 1
请你估计这400户的家庭一个月节约用水的总量大约是( )
A.2600立方米 B.1350立方米 C.1300立方米 D.1200立方米
7.对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分4个等级,将调查结果绘制成如下条形统计图和扇形统计图根据图中信息,这些学生的平均分是( )分
A.2.5 B.2.95 C.3 D.3.25
二、填空题:
8.在求n个数的平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n),那么这n个数的平均数也叫做x1,x2,…,xk这k个数的___________,其中f1,f2,…,fk分别叫做x1,x2,…,xk的___________.
9.一个射击运动员连续射靶10次,其中1次射中10环,4次射中9环,3次射中8环,2次射中7环,这个射击运动员本次打靶射中环数的平均数是______环.
10.抽测一批电动单车的性能,得到如下条形统计图,则该批电动单车一次充电后行驶的平均里程数为______千米.
11.某地区月份某一周每天的日最高气温(单位:)如下图所示:
则这周最高气温的平均值是______.
12.某校开展了“书香校园”的活动,八年(2)班班长统计了本学期全班40名同学课外图书的阅读数量(单位:本),绘制了折线统计图(如图所示),在这40名学生的图书阅读数量中,平均每位同学的阅读数量是________.
13.我县疫情封控“解封”以后,某水果店销售元、元、元三种价格的水果,根据水果店一天这三种水果销售量的统计图(如图),可计算出该店当天销售出这三种水果的平均价格是______元.
三、解答题:
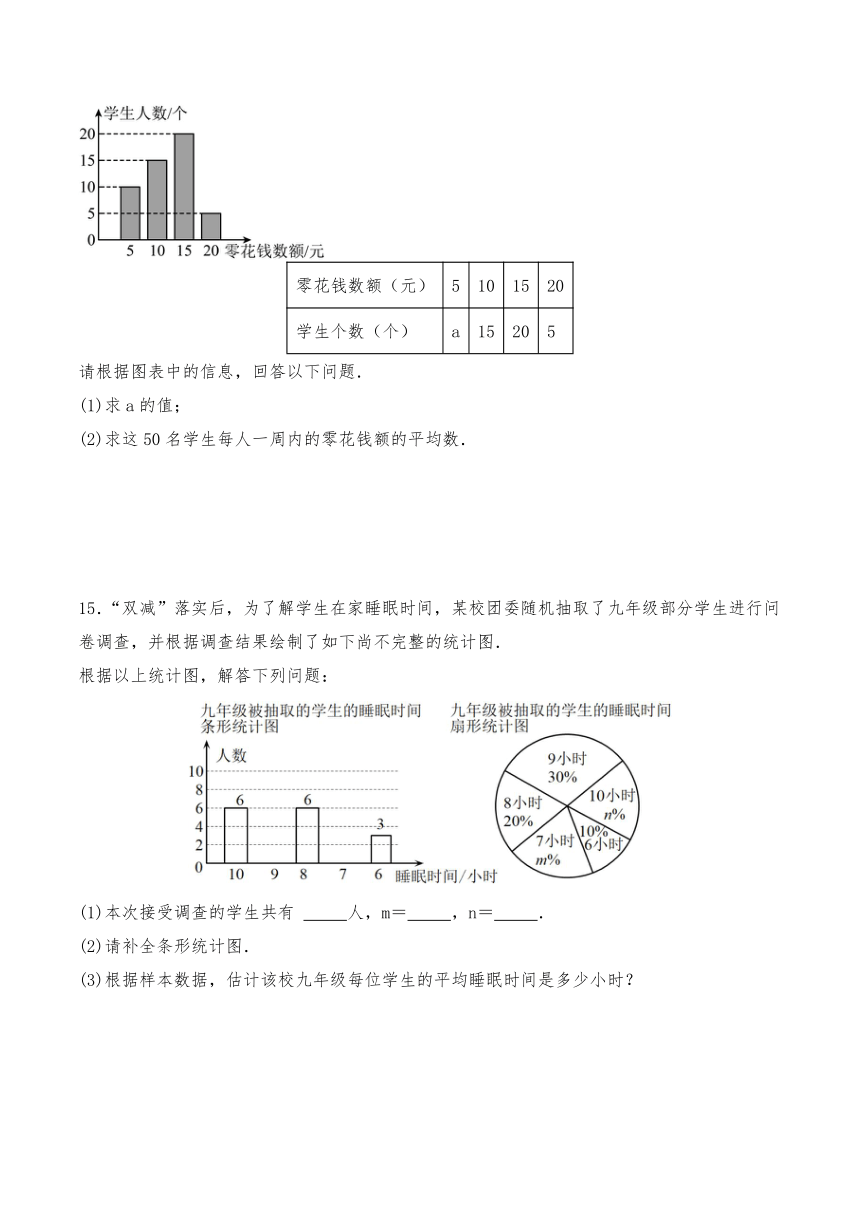
14.某教师为了对学生票在钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了统计图表如图所示的统计图.
零花钱数额(元) 5 10 15 20
学生个数(个) a 15 20 5
请根据图表中的信息,回答以下问题.
(1)求a的值;
(2)求这50名学生每人一周内的零花钱额的平均数.
15.“双减”落实后,为了解学生在家睡眠时间,某校团委随机抽取了九年级部分学生进行问卷调查,并根据调查结果绘制了如下尚不完整的统计图.
根据以上统计图,解答下列问题:
(1)本次接受调查的学生共有 人,m= ,n= .
(2)请补全条形统计图.
(3)根据样本数据,估计该校九年级每位学生的平均睡眠时间是多少小时?
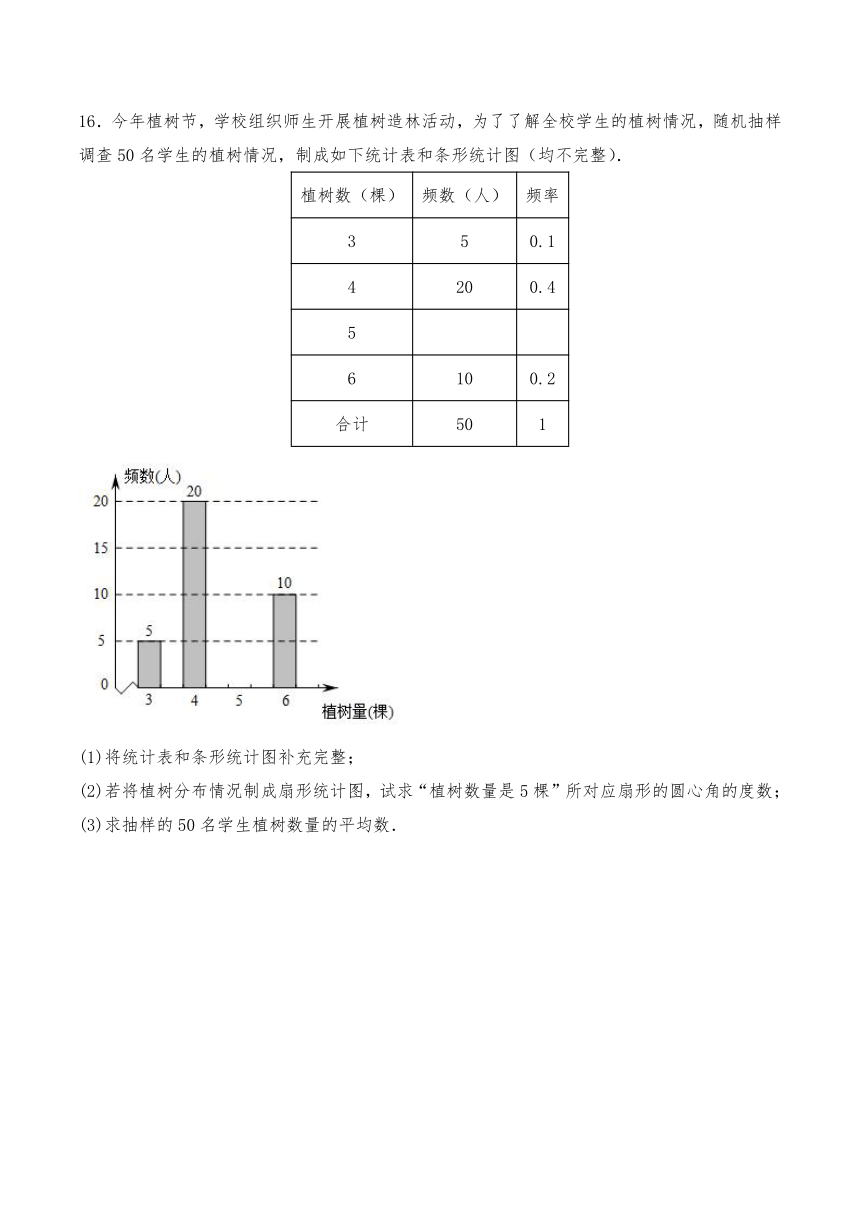
16.今年植树节,学校组织师生开展植树造林活动,为了了解全校学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
植树数(棵) 频数(人) 频率
3 5 0.1
4 20 0.4
5
6 10 0.2
合计 50 1
(1)将统计表和条形统计图补充完整;
(2)若将植树分布情况制成扇形统计图,试求“植树数量是5棵”所对应扇形的圆心角的度数;
(3)求抽样的50名学生植树数量的平均数.
17.为了了解某校九年级学生的体质健康状况,随机抽取了该校九年级的学生进行测试,将这些学生的测试成绩(分)分为A、B、C、D四个等级:A等级(),B等级(),C等级(),D等级();并绘制成如图所示的两幅统计图.
根据以上信息,解答下列问题:
(1)在抽取的学生中,D等级的学生人数所占的百分比是__________.
(2)在抽取的学生中,C等级的学生为8人,请估计该校九年级学生中A等级的学生人数.
(3)计算所抽取学生测试的平均成绩.
18.为落实“双减”和“五项管理”,促进每一个孩子全面发展、健康成长,各级各部门都做出了有力举措.某班同学分三组进行教学实践活动调查,三组同学分别对七年级40名同学作业管理情况,八年级30名同学读物管理情况,九年级30名同学睡眠管理情况进行全面调查,并分别用扇形图、频数分布直方图、表格来描述得到的数据.
九年级同学睡眠管理时间情况统计表
时间 9小时左右 10小时左右 11小时左右 8小时左右
人数(人) 5 8 12 5
根据以上信息,请回答下列问题:
(1)七年级40名同学中必做作业的人数是多少?
(2)补全八年级30名同学读物管理情况频数分布直方图:
(3)九年级30名同学睡眠时间的平均时间大约是多少小时?
19.某校为进一步深化全民阅读和书香阜宁建设,随机抽取了八年级若干名学生,对“双减”后学生周末课外阅读时间进行了调查.根据收集到的数据,整理后得到下列不完整的图表,请你根据图表中提供的信息,解答下面的问题:
时间/分钟
组中值 75 105 135
频数/人 6 20 4
(1)扇形统计图中,120~150分钟时间段对应扇形的圆心角的度数是______;______;
(2)表格中______,______;
(3)请通过计算估计该校八年级学生周末课外平均阅读时间.
答案
一、单选题:
1.A
【分析】根据加权平均数公式求解即可.
【详解】解:根据题意得:
(岁),
答:这个班级学生的平均年龄是14岁.
故选:A.
2.C
【分析】求出甲乙丙三种糖果的加权平均数,即可求解.
【详解】,
答:为确保不亏本,售价至少应定为每千克6.7元.
故选C.
3.B
【分析】根据平均数的求法列式求解即可.
【详解】由题意得
,
解之得
x=1.
经检验,x=1符合题意.
故选B.
4.C
【分析】根据平均数的计算方法进行计算即可.
【详解】解:,
故选:C.
5.C
【分析】利用加权平均数的公式求解即可.
【详解】解:根据题意,可得这10名学生一周做家务劳动的平均时间是:
.
故选:C.
6.D
【分析】计算20户的平均数,再乘以总户数400即可.
【详解】解:(立方米),
∴这400户的家庭一个月节约用水的总量大约是1200立方米,
故选:D.
7.B
【分析】根据成绩为4分的人数是12,占比为30%,求出总人数,然后分别求出成绩为2分,3分的人数,然后求加权平均数即可.
【详解】解:由得4分的频数12,频率30%,得总量12÷30%=40.
由得3分的频率42.5%,得频数40×42.5%=17.
由得1 分的频数3,得频率3÷40=7.5%.
∴得2分的频率为1-(7.5%+42.5%+30%)=20%.
∴这些学生的平均分数是:1×7.5%+2×20%+3×42.5%+4×30%=2.95.
故选B.
二、填空题:
8. 加权平均数 权
9.
【分析】利用加权平均数公式即可求解.
【详解】解:这个射击运动员本次打靶射中环数的平均数是:
(环)
故答案为:
10.59.5
【分析】根据加权平均数的公式计算可得.
【详解】解:根据题意得:该批电动单车一次充电后行使的平均里程数为
千米
故答案为:59.5
11.
【分析】按照计算加权平均数的方法计算即可.
【详解】解:根据图表可得,
,
则这周最高气温的平均值是,
故答案为:.
12.22.5本
【分析】根据折线统计图中数据,利用加权平均数的定义列式计算可得.
【详解】解:平均每位同学的阅读数量是(本),
故答案为:22.5本.
13.
【分析】根据加权平均数的计算方法,分别用单价乘以相应的百分比,计算即可得解.
【详解】解:该店当月销售出水果的平均价格是(元,
故答案为:15.3.
三、解答题:
14.(1)解:因为总人数50 ,所以a=50-15-5-20=10
(2)=12;
15.(1)本次抽样调查的样本容量是,
,
故;
,
故;
故答案为:.
(2)9小时的人数为:(人),
7小时的人数为:(人),
补全条形统计图如下:
(3)(小时),
答:估计该校九年级每位学生的平均睡眠时间大约是小时.
16.(1)解:植树棵树为5棵的人数为,频率为;
补全统计表如下,
植树数(棵) 频数(人) 频率
合计
故答案为:.
补全统计图如图所示,
(2)“植树数量是5棵”所对应扇形的圆心角的度数为
(3)抽样的50名学生植树数量的平均数为棵
17.(1)解:在抽取的学生中D等级的学生人数所占的百分比,
故答案为.
(2)∵(人),(人)
∴(人)
∴估计该校九年级学生中A等级的学生人数200人
(3)∵(分)
∴所抽取学生测试的平均成绩分
18.(1)
解:(人)
答:七年级40名同学中必做作业的人数是16人.
(2)
科普类的人数有:.
如图:该频数分布直方图为所求.
(3)
(小时).
答:九年级30名同学睡眠时间的平均时间大约是9.9小时.
19.(1)∵根据扇形统计图中,120~150分钟时间段的占比为10%
∴120~150分钟时间段对应扇形的圆心角的度数为
∵120~150分钟时间段的人数为4人
∴调查总人数为人
∴90~120分钟时间段的人数为人
∴90~120分钟时间段的人数与总人数的比为
∴
(2)30~60分钟时间段组中值为,故;
90~120分钟时间段的频数/人为,故.
(3)30~60分钟时间段的调查人数占总人数的比例为;
60~90分钟时间段的调查人数占总人数的比例为;
90~120分钟时间段的调查人数占总人数的比例为;
120~140分钟时间段的调查人数占总人数的比例为;
∴八年级学生周末课外平均阅读时间为:分钟
∴该校八年级学生周末课外平均阅读时间为84分钟.
一、单选题:
1.某校九年级甲班40名学生中,5人13岁,30人14岁,5人15岁,则这个班级学生的平均年龄为( )
A.14岁 B.14.5岁 C.13.5岁 D.15岁
2.甲、乙、丙三种糖果的售价分别为每千克6元、7元、8元,若将甲种10千克、乙种9千克、丙种3千克混在一起出售,为确保不亏本,售价至少应定为每千克( )
A.6元 B.6.5元 C.6.7元 D.7元
3.下表中,若平均数为2,则x等于( ).
A.0 B.1 C.2 D.3
4.王老师为了了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,将获得的数据绘制成如图所示的条形图,则这10名学生周末学均时间为( )
A.1.7 B.3 C.3.3 D.3.7
5.为了了解学生参与家务劳动情况,某老师在所任教班级随机调查了10名学生一周做家务劳动的时间,其统计数据如表:
时间(单位:小时) 4 3 2 1 0
人数 2 4 2 1 1
则这10名学生一周做家务劳动的平均时间是( )小时.
A.3.5 B.3 C.2.5 D.2
6.某小区开展节约每一滴水活动,为了了解开展活动一个月以来节约用水的情况,从400户中随机选取20户统计了各自家庭一个月节约用水情况.表格如下:
节水量/立方米 2 2.5 3 4 0
家庭数/户 2 4 6 7 1
请你估计这400户的家庭一个月节约用水的总量大约是( )
A.2600立方米 B.1350立方米 C.1300立方米 D.1200立方米
7.对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分4个等级,将调查结果绘制成如下条形统计图和扇形统计图根据图中信息,这些学生的平均分是( )分
A.2.5 B.2.95 C.3 D.3.25
二、填空题:
8.在求n个数的平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n),那么这n个数的平均数也叫做x1,x2,…,xk这k个数的___________,其中f1,f2,…,fk分别叫做x1,x2,…,xk的___________.
9.一个射击运动员连续射靶10次,其中1次射中10环,4次射中9环,3次射中8环,2次射中7环,这个射击运动员本次打靶射中环数的平均数是______环.
10.抽测一批电动单车的性能,得到如下条形统计图,则该批电动单车一次充电后行驶的平均里程数为______千米.
11.某地区月份某一周每天的日最高气温(单位:)如下图所示:
则这周最高气温的平均值是______.
12.某校开展了“书香校园”的活动,八年(2)班班长统计了本学期全班40名同学课外图书的阅读数量(单位:本),绘制了折线统计图(如图所示),在这40名学生的图书阅读数量中,平均每位同学的阅读数量是________.
13.我县疫情封控“解封”以后,某水果店销售元、元、元三种价格的水果,根据水果店一天这三种水果销售量的统计图(如图),可计算出该店当天销售出这三种水果的平均价格是______元.
三、解答题:
14.某教师为了对学生票在钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了统计图表如图所示的统计图.
零花钱数额(元) 5 10 15 20
学生个数(个) a 15 20 5
请根据图表中的信息,回答以下问题.
(1)求a的值;
(2)求这50名学生每人一周内的零花钱额的平均数.
15.“双减”落实后,为了解学生在家睡眠时间,某校团委随机抽取了九年级部分学生进行问卷调查,并根据调查结果绘制了如下尚不完整的统计图.
根据以上统计图,解答下列问题:
(1)本次接受调查的学生共有 人,m= ,n= .
(2)请补全条形统计图.
(3)根据样本数据,估计该校九年级每位学生的平均睡眠时间是多少小时?
16.今年植树节,学校组织师生开展植树造林活动,为了了解全校学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
植树数(棵) 频数(人) 频率
3 5 0.1
4 20 0.4
5
6 10 0.2
合计 50 1
(1)将统计表和条形统计图补充完整;
(2)若将植树分布情况制成扇形统计图,试求“植树数量是5棵”所对应扇形的圆心角的度数;
(3)求抽样的50名学生植树数量的平均数.
17.为了了解某校九年级学生的体质健康状况,随机抽取了该校九年级的学生进行测试,将这些学生的测试成绩(分)分为A、B、C、D四个等级:A等级(),B等级(),C等级(),D等级();并绘制成如图所示的两幅统计图.
根据以上信息,解答下列问题:
(1)在抽取的学生中,D等级的学生人数所占的百分比是__________.
(2)在抽取的学生中,C等级的学生为8人,请估计该校九年级学生中A等级的学生人数.
(3)计算所抽取学生测试的平均成绩.
18.为落实“双减”和“五项管理”,促进每一个孩子全面发展、健康成长,各级各部门都做出了有力举措.某班同学分三组进行教学实践活动调查,三组同学分别对七年级40名同学作业管理情况,八年级30名同学读物管理情况,九年级30名同学睡眠管理情况进行全面调查,并分别用扇形图、频数分布直方图、表格来描述得到的数据.
九年级同学睡眠管理时间情况统计表
时间 9小时左右 10小时左右 11小时左右 8小时左右
人数(人) 5 8 12 5
根据以上信息,请回答下列问题:
(1)七年级40名同学中必做作业的人数是多少?
(2)补全八年级30名同学读物管理情况频数分布直方图:
(3)九年级30名同学睡眠时间的平均时间大约是多少小时?
19.某校为进一步深化全民阅读和书香阜宁建设,随机抽取了八年级若干名学生,对“双减”后学生周末课外阅读时间进行了调查.根据收集到的数据,整理后得到下列不完整的图表,请你根据图表中提供的信息,解答下面的问题:
时间/分钟
组中值 75 105 135
频数/人 6 20 4
(1)扇形统计图中,120~150分钟时间段对应扇形的圆心角的度数是______;______;
(2)表格中______,______;
(3)请通过计算估计该校八年级学生周末课外平均阅读时间.
答案
一、单选题:
1.A
【分析】根据加权平均数公式求解即可.
【详解】解:根据题意得:
(岁),
答:这个班级学生的平均年龄是14岁.
故选:A.
2.C
【分析】求出甲乙丙三种糖果的加权平均数,即可求解.
【详解】,
答:为确保不亏本,售价至少应定为每千克6.7元.
故选C.
3.B
【分析】根据平均数的求法列式求解即可.
【详解】由题意得
,
解之得
x=1.
经检验,x=1符合题意.
故选B.
4.C
【分析】根据平均数的计算方法进行计算即可.
【详解】解:,
故选:C.
5.C
【分析】利用加权平均数的公式求解即可.
【详解】解:根据题意,可得这10名学生一周做家务劳动的平均时间是:
.
故选:C.
6.D
【分析】计算20户的平均数,再乘以总户数400即可.
【详解】解:(立方米),
∴这400户的家庭一个月节约用水的总量大约是1200立方米,
故选:D.
7.B
【分析】根据成绩为4分的人数是12,占比为30%,求出总人数,然后分别求出成绩为2分,3分的人数,然后求加权平均数即可.
【详解】解:由得4分的频数12,频率30%,得总量12÷30%=40.
由得3分的频率42.5%,得频数40×42.5%=17.
由得1 分的频数3,得频率3÷40=7.5%.
∴得2分的频率为1-(7.5%+42.5%+30%)=20%.
∴这些学生的平均分数是:1×7.5%+2×20%+3×42.5%+4×30%=2.95.
故选B.
二、填空题:
8. 加权平均数 权
9.
【分析】利用加权平均数公式即可求解.
【详解】解:这个射击运动员本次打靶射中环数的平均数是:
(环)
故答案为:
10.59.5
【分析】根据加权平均数的公式计算可得.
【详解】解:根据题意得:该批电动单车一次充电后行使的平均里程数为
千米
故答案为:59.5
11.
【分析】按照计算加权平均数的方法计算即可.
【详解】解:根据图表可得,
,
则这周最高气温的平均值是,
故答案为:.
12.22.5本
【分析】根据折线统计图中数据,利用加权平均数的定义列式计算可得.
【详解】解:平均每位同学的阅读数量是(本),
故答案为:22.5本.
13.
【分析】根据加权平均数的计算方法,分别用单价乘以相应的百分比,计算即可得解.
【详解】解:该店当月销售出水果的平均价格是(元,
故答案为:15.3.
三、解答题:
14.(1)解:因为总人数50 ,所以a=50-15-5-20=10
(2)=12;
15.(1)本次抽样调查的样本容量是,
,
故;
,
故;
故答案为:.
(2)9小时的人数为:(人),
7小时的人数为:(人),
补全条形统计图如下:
(3)(小时),
答:估计该校九年级每位学生的平均睡眠时间大约是小时.
16.(1)解:植树棵树为5棵的人数为,频率为;
补全统计表如下,
植树数(棵) 频数(人) 频率
合计
故答案为:.
补全统计图如图所示,
(2)“植树数量是5棵”所对应扇形的圆心角的度数为
(3)抽样的50名学生植树数量的平均数为棵
17.(1)解:在抽取的学生中D等级的学生人数所占的百分比,
故答案为.
(2)∵(人),(人)
∴(人)
∴估计该校九年级学生中A等级的学生人数200人
(3)∵(分)
∴所抽取学生测试的平均成绩分
18.(1)
解:(人)
答:七年级40名同学中必做作业的人数是16人.
(2)
科普类的人数有:.
如图:该频数分布直方图为所求.
(3)
(小时).
答:九年级30名同学睡眠时间的平均时间大约是9.9小时.
19.(1)∵根据扇形统计图中,120~150分钟时间段的占比为10%
∴120~150分钟时间段对应扇形的圆心角的度数为
∵120~150分钟时间段的人数为4人
∴调查总人数为人
∴90~120分钟时间段的人数为人
∴90~120分钟时间段的人数与总人数的比为
∴
(2)30~60分钟时间段组中值为,故;
90~120分钟时间段的频数/人为,故.
(3)30~60分钟时间段的调查人数占总人数的比例为;
60~90分钟时间段的调查人数占总人数的比例为;
90~120分钟时间段的调查人数占总人数的比例为;
120~140分钟时间段的调查人数占总人数的比例为;
∴八年级学生周末课外平均阅读时间为:分钟
∴该校八年级学生周末课外平均阅读时间为84分钟.
