人教版八年级数学下册 期末复习测试卷 (含详解)
文档属性
| 名称 | 人教版八年级数学下册 期末复习测试卷 (含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 781.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-04 09:13:39 | ||
图片预览




文档简介
期末复习测试卷
一、选择题(本题共12小题,每小题3分,共36分)
1.代数式有意义时,x应满足的条件为( )
A.x>﹣1 B.x≥﹣1 C.x<﹣1 D.x≠﹣1
2.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,下列条件中,不能判定△ABC是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3 B.∠A+∠B=90°
C.a:b:c=2:3:4 D.b2=a2﹣c2
3.矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相垂直平分
4.关于一次函数y=﹣2x+4,下列说法不正确的是( )
A.图象不经过第三象限 B.y随着x的增大而减小
C.图象与x轴交于(﹣2,0) D.图象与y轴交于(0,4)
5.如图,A,B两地被池塘隔开,小明在AB外选一点C,连接AC,BC,分别取AC,BC的中点D,E,为了测量A,B两地间的距离,则可以选择测量以下线段中哪一条的长度( )
A.AC B.AD C.DE D.CD
6.如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.3和4之间 B.4和5之间 C.﹣4和﹣3之间 D.﹣5和﹣4之间
7.近日,杭州亚运会游泳选拔赛已开赛,其中参加男子100米自由泳的甲、乙、丙、丁四位运动员的5次比赛的平均成绩和方差S2如表所示:
甲 乙 丙 丁
(秒) 48.67 49.05 48.67 49.03
S2(秒2) 0.03 0.07 0.06 0.04
若要选拔一名速度快且发挥稳定的运动员参加亚运会集训营,根据表中数据应选择( )
A.甲 B.乙 C.丙 D.丁
8.在平面直角坐标系中,以O(0,0),A(1,2),B(4,0)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
A.(﹣3,2) B.(﹣2,2) C.(5,2) D.(3,﹣2)
9.如图,在Rt△ABC中,CD为斜边AB上的中线,点E是AB上方一点,且AE=BE,连接DE,若CD=3,AE=7,则DE的长为( )
A.2 B.2 C.4 D.4
10.如图,一次函数y=kx+b(k>0)的图象过点(﹣1,0),则不等式k(x﹣1)+b<0的解集是( )
A.x<﹣2 B.x<﹣1 C.x<0 D.x<1
11.甲、乙两地之间是一条直路,在全民健身活动中,嘉嘉跑步从甲地往乙地,琪琪骑自行车从乙地往甲地,两人同时出发,琪琪先到达目的地,两人之间的距离s(km)与运动时间t(h)的函数关系大致如图所示,下列说法中错误的是( )
A.两人出发1小时后相遇
B.嘉嘉跑步的速度为8km/h
C.琪琪到达目的地时两人相距10km
D.琪琪比嘉嘉提前1.5h到达目的地
12.如图,正方形ABCD的边长为4,点E从点A出发沿着线段AD向点D运动(不与点A、D重合),同时点F从点D出发沿着线段DC向点C运动(不与点D、C重合),点E与点F的运动速度相同.BE与AF相交于点G.则有下列结论:①∠BGF是定值;②FB平分∠AFC;③当E运动到AD中点时,CG=AB;④当四边形GEDF的面积是2时,点G到直线CD的距离为3.其中正确的是( )
A.①②③ B.①③④ C.①③ D.①④
二、填空题(本题共4个小题,每小题4分,共16分)
13.若,则x2﹣2x+1= .
14.小红在一张菱形纸片中剪掉一个正方形,做成班刊刊头(如图所示).若菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则这张菱形纸片的边长为 cm.
15.在平面直角坐标系中,已知正方形OABC,其中点A(﹣4,0),B(﹣4,4),C(0,4).给出如下定义:若点P向上平移2个单位,再向左平移3个单位后得到P′,点P′在正方形OABC的内部或边上,则称点P为正方形OABC的“和谐点”,若在直线y=kx+6上存在点Q,使得点Q是正方形OABC的“和谐点”,则k的取值范围是 .
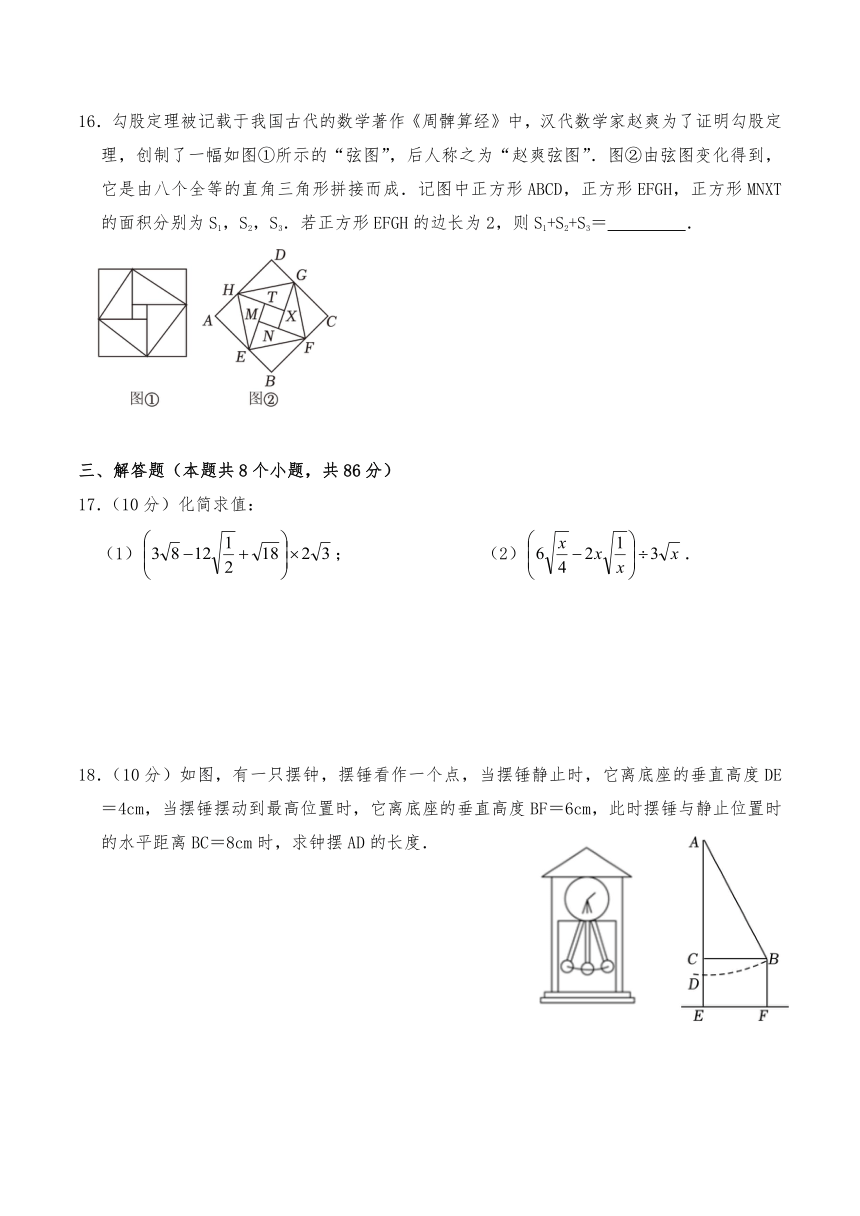
16.勾股定理被记载于我国古代的数学著作《周髀算经》中,汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.图②由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNXT的面积分别为S1,S2,S3.若正方形EFGH的边长为2,则S1+S2+S3= .
三、解答题(本题共8个小题,共86分)
17.(10分)化简求值:
(1); (2).
18.(10分)如图,有一只摆钟,摆锤看作一个点,当摆锤静止时,它离底座的垂直高度DE=4cm,当摆锤摆动到最高位置时,它离底座的垂直高度BF=6cm,此时摆锤与静止位置时的水平距离BC=8cm时,求钟摆AD的长度.
19.(10分)某校为了解学生对共青团的认识,组织七、八年级全体学生进行了“团史知识”竞赛,为了解竞赛成绩,现从该校七、八年级中各随机抽取10名学生的竞赛成绩(满分100分,90分及90分以上为优秀)进行整理、描述和分析(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100,下面给出了部分信息:
七年级抽取的10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82;
八年级抽取的10名学生的竞赛成绩在C组中的数据是:94,90,91;
七,八年级抽取的学生竞赛成绩统计表:
年级 平均数 中位数 众数 方差
七年级 92 93 c 52
八年级 92 b 100 50.4
根据以上信息,解答下列问题:
(1)图表中a= ,b= ,c= ;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握团史知识较好?请说明理由(一条理由即可);
(3)该校七年级有450人,八年级有500人参加了此次“团史知识”竞赛,估计参加竞赛活动成绩优秀的学生人数是多少?
20.(10分)如图,在四边形ABCD中,AB=CD,BC=AD,分别过点A、点C作AE⊥BC、CF⊥AD,垂足分别为E、F.
(1)判断四边形AECF的形状,并说明理由;
(2)若∠B=60°,AB=4,点E是BC的中点,求四边形ABCD的面积.
21.(10分)甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一”假期,两家均推出了优惠方案,甲采摘园的优惠方案:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y甲(元),在乙采摘园所需总费用为y乙(元),图中折线O﹣A﹣B表示y乙与x之间的函数关系.
(1)求y甲与x之间的函数关系式、y乙与x(只求x>10时直线AB)的函数关系式;
(2)当游客采摘15千克的草莓时,你认为他在哪家草莓园采摘更划算?
22.(12分)在数学小组探究学习中,张兵与他的小组成员遇到这样一道题:
已知,求2a2﹣8a+1的值.他们是这样解答的:
∵
∴
∴(a﹣2)2=3即a2﹣4a+4=3
∴a2﹣4a=﹣1
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据张兵小组的解题方法和过程,解决以下问题:
(1)= .
(2)化简;
(3)若,求a4﹣4a3﹣4a+3的值.
23.(12分)如图,在△ABC中,∠ACB=90°,AB=5,BC=3,点P从点A出发,沿射线AC以每秒2个单位长度的速度运动.设点P的运动时间为t秒(t>0).
(1)当点P在AC的延长线上运动时,CP的长为 ;(用含t的代数式表示)
(2)若点P在∠ABC的角平分线上,求t的值;
(3)在整个运动中,直接写出△ABP是等腰三角形时t的值.
24.(12分)如图,平面直角坐标系中,A(0,1),M(4,3),N(5,5),动点P从点A出发,沿y轴以每秒2个单位的速度向上移动,且过点P的直线l(其解析式为y=﹣x+b,且直线与x轴所夹的锐角为45°)也随之移动,设移动时间为t秒.【“中点坐标公式”:如果点A(x1,y1)、B(x2,y2),则线段AB的中点坐标为.如:A(2,﹣3)、B(4,1),则线段AB的中点坐标为(3,﹣1).此公式在以下解题中如有需要可以直接使用.】
(1)填空:当t=3时,直线l的解析式为 ;
(2)若点M,N位于直线l的异侧,求t的取值范围;
(3)求出t为何值时,点M关于直线l的对称点落在坐标轴上.
25.(12分)阅读下面的例题及点拨,并解决问题:
如图①,在等边△ABC中,M是BC边上一点(不含端点B,C),N是△ABC的外角∠ACH的平分线上一点,且AM=MN.求证:∠AMN=60°.
(1)点拨:如图②,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连接EM.易证:△ABM≌△EBM(SAS),请完成剩余证明过程:
(2)拓展:如图③,在正方形A1B1C1D1中,M1是B1C1边上一点(不含端点B1,C1),N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点,且A1M1=M1N1.求证:∠A1M1N1=90°.
答案
一、选择题
1.
【分析】根据分式有意义的条件和二次根式有意义的条件进行求解即可.
【解答】解:∵代数式有意义,
∴,
∴x>﹣1,
故选:A.
2.
【分析】根据三角形内角和定理可判断A、B是否是直角三角形;根据勾股定理逆定理可判断C、D 是否是直角三角形.
【解答】解:A、∵∠A:∠B:∠C=1:2:3,
∴∠A+∠B=∠C,
∵∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,不符合题意;
B、∵∠A+∠B=90°,
∴∠C=180°﹣90°=90°,
∴△ABC是直角三角形,不符合题意;
C、设a=2x,b=3x,c=4x,
∵a2+b2=4x2+9x2=13x2,c2=16x2,a2+b2≠c2,
∴△ABC不是直角三角形,符合题意;
D、∵b2+c2=a2符合勾股定理逆定理,
∴△ABC是直角三角形,不符合题意.
故选:C.
3.
【分析】由矩形的性质和平行四边形的性质即可得出结论.
【解答】解:∵矩形的对边平行且相等,对角线互相平分且相等;
平行四边形的对边平行且相等,对角线互相平分;
∴矩形具有而平行四边形不具有的性质是对角线相等;
故选:A.
4.
【分析】由k=﹣2<0,b=4>0,可得图象经过一、二、四象限,y随x的增大而减小,再分别求解一次函数与坐标轴的交点坐标,从而可得答案.
【解答】解:∵y=﹣2x+4,k=﹣2<0,b=4>0,
∴图象经过一、二、四象限,y随x的增大而减小,
故A,B不符合题意;
当y=0时,﹣2x+4=0,解得x=2,
∴图象与x轴交于(2,0),故C符合题意;
当x=0时,y=4,
∴图象与y轴交于(0,4),故D不符合题意;
故选:C.
5.
【分析】根据中位线定理可得:AB=2DE.
【解答】解:∵D是AC的中点,E是BC的中点,
∴DE是△ABC的中位线,
∴,
∴AB=2DE,
故选:C.
6.
【分析】先根据勾股定理求出OP的长,由于OP=OA,故估算出OP的长,再根据点A在x轴的负半轴上即可得出结论.
【解答】解:∵点P坐标为(﹣2,3),
∴OP==,
∵点A、P均在以点O为圆心,以OP为半径的圆上,
∴OA=OP=,
∵9<13<16,
∴3<<4.
∵点A在x轴的负半轴上,
∴点A的横坐标介于﹣4和﹣3之间.
故选:C.
7.
【分析】此题有两个要求:①平均成绩较低,②状态稳定.于是应选平均数较小、方差较小的运动员参赛.
【解答】解:甲和丙的平均数较小,所以在甲和丙两人中选一人参加比赛,
由于甲的方差比丙小,所以甲更稳定,故选甲参加比赛.
故选:A.
8.
【分析】利用图象法画出平行四边形,可得结论.
【解答】解:如图平行四边形的第三个顶点坐标为(5,2),(﹣3,2),(3,﹣2).
故选:B.
9.
【分析】先利用直角三角形斜边上的中线性质可得CD=AD=BD=3,然后利用等腰三角形的三线合一性质可得ED⊥AD,从而在Rt△ADE中,利用勾股定理进行计算即可解答.
【解答】解:在Rt△ABC中,CD为斜边AB上的中线,
∴CD=AD=BD=AB=3,
∵AE=BE=7,
∴ED⊥AD,
在Rt△ADE中,DE===2,
故选:B.
10.
【分析】将点代入函数解析式,得到k=b,然后将不等式k(x﹣1)+b<0转化为函数y=kx+k<k的解集即可.
【解答】解:∵一次函数y=kx+b(k>0)的图象过点(﹣1,0),
∴0=﹣k+b,即k=b,
∴y=kx+k,
∴A(0,k)
∵k(x﹣1)+b<0,
∴kx﹣k+b<0,即kx+b<k,
∴kx+k<k,即求y=kx+k<k,
由图可知,kx+k<k的部分是点A的左侧部分,
∴k(x﹣1)+b<0的解集是x<0.
故选:C.
11.
【分析】根据函数图象中的数据,可以分别计算出两人的速度,从而可以判断各个选项中的说法是否正确,从而可以解答本题.
【解答】解:由图象可知,
两人出发1小时后相遇,故选项A正确,不符合题意;
嘉嘉跑步的速度为24÷3=8(km/h),故选项B正确,不符合题意;
琪琪的速度为:24÷1﹣8=16(km/h),
琪琪从开始至到达目的地用的时间为:24÷16=1.5(h),
∴琪琪到达目的地时两人相距8×1.5=12(km),故选项C错误,符合题意;
琪琪比嘉嘉提前3﹣1.5=1.5(h)到目的地,故选项D正确,不符合题意;
故选:C.
12.
【分析】根据正方形的性质,三角形全等的判定和性质,角的平分线的意义,点到直线的距离计算判断即可.
【解答】解:∵正方形ABCD,
∴AB=AD,∠BAE=∠ADF=90°,∠AEB+∠ABE=90°,
在△BAE和△ADF中,
,
∴△BAE≌△ADF(SAS),
∴∠DAF=∠ABE,
∴∠AEB+∠DAF=90°,
∴∠AGE=∠BGF=90°,
∴∠BGF是定值,
故①正确;
设FB平分∠AFC,
∵BG⊥AF,BC⊥CF,
∴BG=BC,AB>BG,
∵正方形ABCD,
∴AB=BC,
∴BG=BC,BC>BG,
矛盾,故假设不成立,
故②错误;
延长AF,交BC的延长线于点H,
根据(1)得,△BAE≌△ADF,∠BGF=90°,
∴AE=DF,
∵E是AD中点,
∴,
∵正方形ABCD,
∴AD=DC,
∴,
∴DF=FC;
∵正方形ABCD,
∴∠HCF=∠ADF=90°,
在△HCF和△ADF中,
,
∴△HCF≌△ADF(ASA),
∴AD=CH,
∴AD=CH=BC,
∴,
∴CG=AB,
故③正确;
过点G作QK⊥DC于点K,交AB于点Q,
∵正方形ABCD,
∴∠QAD=∠ADK=90°,
∴四边形AQKD是矩形,
∴QK=AD=4,QK⊥AB,
根据①得,△BAE≌△ADF,
∴S△BAE=S△ADF,
∴S△BAE﹣S△AGF=S△ADF﹣S△AGF,
∴S△BAG=S四边形DEGF=2,
∴,
∴,
解得QG=1,
∴GK=QK﹣QG=4﹣1=3,
故当四边形GEDF的面积是2时,点G到直线CD的距离为3,
故④正确,
故选:B.
二、填空题
13.
【分析】先利用完全平方公式对代数式变形,然后代值求解即可.
【解答】解:∵,
∴x2﹣2x+1=(x﹣1)2===2023,
故答案为:2023.
14.
【分析】连接AC,BD,根据正方形AECF的面积为50cm2,菱形ABCD的面积为120cm2,求出AC和BD,即可得出答案.
【解答】解:如图,连接AC,BD,
∵正方形AECF的面积为50cm2,
∴AC=×=10(cm),
∵菱形ABCD的面积为120cm2,
∴BD=2×120÷10=24(cm),
∴菱形ABCD的边长为=13(cm),
故答案为:13.
15.
【分析】由在直线y=kx+6上存在点Q,使得点Q是正方形OABC的“和谐点”,可知Q′在直线y=k(x+3)+8上,求得直线经过点A时的k的值,即可求得k的取值范围.
【解答】解:直线y=kx+6向上平移2个单位,再向左平移3个单位后得到y=k(x+3)+8,
把B(﹣4,4)代入得﹣k+8=4,解得k=4,
∴0<k≤4.
故答案为:0<k≤4.
16.
【分析】设全等的直角三角形的两条直角边为a、b且a>b,则,,,先证明,再证明即可得到答案.
【解答】解:设全等的直角三角形的两条直角边为a、b且a>b,
由题意可知:,,,
∵正方形EFGH的边长为2,
∴,
∴,
=a2+2ab+b2+a2+b2+a2﹣2ab+b2
=3(a2+b2)
=12,
故答案为:12.
三、解答题
17.解:(1)
=
=
=;
(2)
=
=
=.
18.解:设AB=AD=xcm,由题意得,CE=BF=6cm,
∴AC=AD+DE﹣CE=(x﹣2)cm,
∵AC2+BC2=AB2,
∴(x﹣2)2+82=x2,
∴x=17,
∴AD=17cm.
答:钟摆AD的长度.
19.解:(1)C所占的百分比是:×100%=30%,
a%=1﹣30%﹣20%﹣10%=40%,即a=40;
∵共有10个数,中位数是第5、第6个数的平均数,
∴中位数b==90.5;
∵99出现了3次,出现的次数最多,
∴众数c=99.
故答案为:40;90.5;99;
(2)我认为八年级成绩更好,理由如下:
因为两个年级的平均数相同,而八年级的成绩的众数大于七年级,方差小于七年级.
(3)根据题意得:
450×+500×(30%+40%)
=270+350
=620(人),
答:估计参加竞赛活动成绩优秀的学生人数是620人.
20.解:(1)四边形AECF是矩形,
理由:∵AB=CD,BC=AD,
∴四边形ABCD是平行四边形,
∴∠B=∠D,AD∥BC,
∵AE⊥BC、CF⊥AD,
∴∠AEB=∠CFD=90°,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∴AF=CE,
∵∠AEC=90°,
∴四边形AECF是矩形;
(2)∵∠AEB=90°,∠B=60°,AB=4,
∴∠BAE=30°,
∴,AE=AB=2,
∵点E是BC的中点,
∴BC=2BE=4,
∴四边形ABCD的面积=BC AE=4×=8.
21.解:(1)根据题意得,甲、乙两采摘园优惠前的草莓销售价格:300÷10=30(元/千克).
∴y甲=30×0.6x+60=18x+60;
当x≥10时,设y乙=kx+b,
由题意的:,
解得,
∴y乙=12x+180,
∴y乙与x之间的函数关系式为:yz=12x+180(x≥10);
(2)当x=15时,y甲=18×15+60=330,y乙=12×15+180=360,
∴y甲<y乙,
∴他在甲家草莓园采摘更划算.
22.解:(1),
故答案为:;
(2)原式=﹣1+﹣+﹣+…+﹣
=﹣1+﹣+﹣+﹣…﹣+
=
=﹣1+13
=12;
(3)∵,
∴a﹣2=,
∴(a﹣2)2=5,即a2﹣4a+4=5.
∴a2﹣4a=1.
∴a4﹣4a3﹣4a+3=a2(a2﹣4a)﹣4a+3=a2×1﹣4a+3=a2﹣4a+3=1+3=4.
23.解:(1)∵在△ABC中,∠ACB=90°,AB=5,BC=3,
∴由勾股定理得:,
∵已知点P从点A出发,以每秒2个单位长度的速度运动,
∴当点P在AC的延长线上时,点P运动的长度为:AC+CP=2t,
∵AC=4,
∴CP=2t﹣AC=2t﹣4.
故答案为:2t﹣4.
(2)过点P作PM⊥AB于点M,如图所示:
∵∠ACB=90°,
∴PC⊥BC,
∵点P在∠ABC的角平分线上,PM⊥AB,
∴PC=PM,
又∵PB=PB,
∴Rt△PCB≌Rt△PMB(HL),
∴CB=MB,
∴AM=AB﹣MB=AB=BC=5﹣3=2,
设PM=PC=x,则AP=4﹣x,
在Rt△APM中,AM2+PM2=AP2,
∴22+x2=(4﹣x)2,
解得:,
,
即若点P在∠ABC的角平分线上,则t的值为.
(3)当AB作为底边时,如图所示:
则PA=PB,设PA=a,则PC=AC﹣AP=4﹣a,
在Rt△PCB中,PB2=PC2+CB2,
a2=(4﹣a)2+32,
解得:,
此时;
当AB作为腰时,如图所示:
AP1=AB=5,此时;
AB=BP2时,
∵BC⊥AP2,
∴AP2=2AC=8,
此时t=8÷2=4,
综上分析可知,t的值为或或4.
24.解:(1)当t=3时,则点P(0,7),
则直线l的表达式为:y=﹣x+7,
故答案为:y=﹣x+7;
(2)将点M、N的坐标分别代入y=﹣x+b得:
3=﹣4+b,5=﹣5+b,
则b=7,b=10,
则运动的距离分别为:6,9,
则3≤t≤4.5;
(3)作M点关于l的对称点M',如图所示:
连接MM'与x轴交于点F,直线l与x轴交于E点,直线l与MM'交于点H,
则有MM'⊥HE,
∴∠EHF=90°,
∵直线l与x轴所夹的锐角为45°,
∴∠MFE=90°﹣45°=45°,
∴直线MM'解析式中的k=1,设MM'解析式为y=x+n,
代入点M(4,3),解得n=﹣1,
故直线MM'的解析式为:y=x﹣1,
∴设点M'的坐标为(a,a﹣1),
由H是M和M'的中点可知:
H点坐标为(,),即H(a+2,a+1),
情况一:当M'位于x轴上时,即a﹣1=0,即a=1时,
求得H点坐标为(2.5,1.5),
又H点在直线l上,故将H点坐标代入直线l的解析式y=﹣x+b中,
求得b=4,此时l的解析式y=﹣x+4,
∴此时P点坐标为(0,4),
故时间t=(4﹣1)÷2=1.5秒;
情况二:当M'位于y轴上时,即a=0时,
求得H点坐标为(2,1),
又H点在直线l上,故将H点坐标代入直线l的解析式y=﹣x+b中,
求得b=3,此时ll的解析式y=﹣x+3,
∴此时P点坐标为(0,3),
故时间t=(3﹣1)÷2=1秒;
∴t=1.5秒或1秒时,点M关于l的对称点落在坐标轴上.
25.证明:(1)点拨:如图2,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连接EM,
易证△ABM≌△EBM(SAS),
∴AM=EM,∠1=∠2;
∵AM=MN,
∴EM=MN,
∴∠3=∠4;
∵∠3+∠1=∠4+∠5=60°,
∴∠1=∠2=∠5.
∵∠2+∠6=120,
∴∠5+∠6=120°,
∴∠AMN=60°;
(2)拓展:延长AB至E,使EB=AB,连接EMC、EC,如图所示:
则EB=BC,∠EBM中=90°=∠ABM,
∴△EBC是等腰直角三角形,
∴∠BEC=∠BCE=45°,
∵N是正方形ABCD的外角∠DCH的平分线上一点,
∴∠MCN=90°+45°=135°,
∴∠BCE+∠MCN=180°,
∴E、C、N,三点共线,
在△ABM和△EBM中,
,
∴△ABM≌△EBM(SAS),
∴AM=EM,∠1=∠2,
∵AM=MN,
∴EM=MN,
∴∠3=∠4,
∵∠2+∠3=45°,∠4+∠5=45°,
∴∠1=∠2=∠5,
∵∠1+∠6=90°,
∴∠5+∠6=90°,
∴∠AMN=180°﹣90°=90°.
一、选择题(本题共12小题,每小题3分,共36分)
1.代数式有意义时,x应满足的条件为( )
A.x>﹣1 B.x≥﹣1 C.x<﹣1 D.x≠﹣1
2.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,下列条件中,不能判定△ABC是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3 B.∠A+∠B=90°
C.a:b:c=2:3:4 D.b2=a2﹣c2
3.矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相垂直平分
4.关于一次函数y=﹣2x+4,下列说法不正确的是( )
A.图象不经过第三象限 B.y随着x的增大而减小
C.图象与x轴交于(﹣2,0) D.图象与y轴交于(0,4)
5.如图,A,B两地被池塘隔开,小明在AB外选一点C,连接AC,BC,分别取AC,BC的中点D,E,为了测量A,B两地间的距离,则可以选择测量以下线段中哪一条的长度( )
A.AC B.AD C.DE D.CD
6.如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.3和4之间 B.4和5之间 C.﹣4和﹣3之间 D.﹣5和﹣4之间
7.近日,杭州亚运会游泳选拔赛已开赛,其中参加男子100米自由泳的甲、乙、丙、丁四位运动员的5次比赛的平均成绩和方差S2如表所示:
甲 乙 丙 丁
(秒) 48.67 49.05 48.67 49.03
S2(秒2) 0.03 0.07 0.06 0.04
若要选拔一名速度快且发挥稳定的运动员参加亚运会集训营,根据表中数据应选择( )
A.甲 B.乙 C.丙 D.丁
8.在平面直角坐标系中,以O(0,0),A(1,2),B(4,0)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
A.(﹣3,2) B.(﹣2,2) C.(5,2) D.(3,﹣2)
9.如图,在Rt△ABC中,CD为斜边AB上的中线,点E是AB上方一点,且AE=BE,连接DE,若CD=3,AE=7,则DE的长为( )
A.2 B.2 C.4 D.4
10.如图,一次函数y=kx+b(k>0)的图象过点(﹣1,0),则不等式k(x﹣1)+b<0的解集是( )
A.x<﹣2 B.x<﹣1 C.x<0 D.x<1
11.甲、乙两地之间是一条直路,在全民健身活动中,嘉嘉跑步从甲地往乙地,琪琪骑自行车从乙地往甲地,两人同时出发,琪琪先到达目的地,两人之间的距离s(km)与运动时间t(h)的函数关系大致如图所示,下列说法中错误的是( )
A.两人出发1小时后相遇
B.嘉嘉跑步的速度为8km/h
C.琪琪到达目的地时两人相距10km
D.琪琪比嘉嘉提前1.5h到达目的地
12.如图,正方形ABCD的边长为4,点E从点A出发沿着线段AD向点D运动(不与点A、D重合),同时点F从点D出发沿着线段DC向点C运动(不与点D、C重合),点E与点F的运动速度相同.BE与AF相交于点G.则有下列结论:①∠BGF是定值;②FB平分∠AFC;③当E运动到AD中点时,CG=AB;④当四边形GEDF的面积是2时,点G到直线CD的距离为3.其中正确的是( )
A.①②③ B.①③④ C.①③ D.①④
二、填空题(本题共4个小题,每小题4分,共16分)
13.若,则x2﹣2x+1= .
14.小红在一张菱形纸片中剪掉一个正方形,做成班刊刊头(如图所示).若菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则这张菱形纸片的边长为 cm.
15.在平面直角坐标系中,已知正方形OABC,其中点A(﹣4,0),B(﹣4,4),C(0,4).给出如下定义:若点P向上平移2个单位,再向左平移3个单位后得到P′,点P′在正方形OABC的内部或边上,则称点P为正方形OABC的“和谐点”,若在直线y=kx+6上存在点Q,使得点Q是正方形OABC的“和谐点”,则k的取值范围是 .
16.勾股定理被记载于我国古代的数学著作《周髀算经》中,汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.图②由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNXT的面积分别为S1,S2,S3.若正方形EFGH的边长为2,则S1+S2+S3= .
三、解答题(本题共8个小题,共86分)
17.(10分)化简求值:
(1); (2).
18.(10分)如图,有一只摆钟,摆锤看作一个点,当摆锤静止时,它离底座的垂直高度DE=4cm,当摆锤摆动到最高位置时,它离底座的垂直高度BF=6cm,此时摆锤与静止位置时的水平距离BC=8cm时,求钟摆AD的长度.
19.(10分)某校为了解学生对共青团的认识,组织七、八年级全体学生进行了“团史知识”竞赛,为了解竞赛成绩,现从该校七、八年级中各随机抽取10名学生的竞赛成绩(满分100分,90分及90分以上为优秀)进行整理、描述和分析(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100,下面给出了部分信息:
七年级抽取的10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82;
八年级抽取的10名学生的竞赛成绩在C组中的数据是:94,90,91;
七,八年级抽取的学生竞赛成绩统计表:
年级 平均数 中位数 众数 方差
七年级 92 93 c 52
八年级 92 b 100 50.4
根据以上信息,解答下列问题:
(1)图表中a= ,b= ,c= ;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握团史知识较好?请说明理由(一条理由即可);
(3)该校七年级有450人,八年级有500人参加了此次“团史知识”竞赛,估计参加竞赛活动成绩优秀的学生人数是多少?
20.(10分)如图,在四边形ABCD中,AB=CD,BC=AD,分别过点A、点C作AE⊥BC、CF⊥AD,垂足分别为E、F.
(1)判断四边形AECF的形状,并说明理由;
(2)若∠B=60°,AB=4,点E是BC的中点,求四边形ABCD的面积.
21.(10分)甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一”假期,两家均推出了优惠方案,甲采摘园的优惠方案:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y甲(元),在乙采摘园所需总费用为y乙(元),图中折线O﹣A﹣B表示y乙与x之间的函数关系.
(1)求y甲与x之间的函数关系式、y乙与x(只求x>10时直线AB)的函数关系式;
(2)当游客采摘15千克的草莓时,你认为他在哪家草莓园采摘更划算?
22.(12分)在数学小组探究学习中,张兵与他的小组成员遇到这样一道题:
已知,求2a2﹣8a+1的值.他们是这样解答的:
∵
∴
∴(a﹣2)2=3即a2﹣4a+4=3
∴a2﹣4a=﹣1
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据张兵小组的解题方法和过程,解决以下问题:
(1)= .
(2)化简;
(3)若,求a4﹣4a3﹣4a+3的值.
23.(12分)如图,在△ABC中,∠ACB=90°,AB=5,BC=3,点P从点A出发,沿射线AC以每秒2个单位长度的速度运动.设点P的运动时间为t秒(t>0).
(1)当点P在AC的延长线上运动时,CP的长为 ;(用含t的代数式表示)
(2)若点P在∠ABC的角平分线上,求t的值;
(3)在整个运动中,直接写出△ABP是等腰三角形时t的值.
24.(12分)如图,平面直角坐标系中,A(0,1),M(4,3),N(5,5),动点P从点A出发,沿y轴以每秒2个单位的速度向上移动,且过点P的直线l(其解析式为y=﹣x+b,且直线与x轴所夹的锐角为45°)也随之移动,设移动时间为t秒.【“中点坐标公式”:如果点A(x1,y1)、B(x2,y2),则线段AB的中点坐标为.如:A(2,﹣3)、B(4,1),则线段AB的中点坐标为(3,﹣1).此公式在以下解题中如有需要可以直接使用.】
(1)填空:当t=3时,直线l的解析式为 ;
(2)若点M,N位于直线l的异侧,求t的取值范围;
(3)求出t为何值时,点M关于直线l的对称点落在坐标轴上.
25.(12分)阅读下面的例题及点拨,并解决问题:
如图①,在等边△ABC中,M是BC边上一点(不含端点B,C),N是△ABC的外角∠ACH的平分线上一点,且AM=MN.求证:∠AMN=60°.
(1)点拨:如图②,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连接EM.易证:△ABM≌△EBM(SAS),请完成剩余证明过程:
(2)拓展:如图③,在正方形A1B1C1D1中,M1是B1C1边上一点(不含端点B1,C1),N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点,且A1M1=M1N1.求证:∠A1M1N1=90°.
答案
一、选择题
1.
【分析】根据分式有意义的条件和二次根式有意义的条件进行求解即可.
【解答】解:∵代数式有意义,
∴,
∴x>﹣1,
故选:A.
2.
【分析】根据三角形内角和定理可判断A、B是否是直角三角形;根据勾股定理逆定理可判断C、D 是否是直角三角形.
【解答】解:A、∵∠A:∠B:∠C=1:2:3,
∴∠A+∠B=∠C,
∵∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,不符合题意;
B、∵∠A+∠B=90°,
∴∠C=180°﹣90°=90°,
∴△ABC是直角三角形,不符合题意;
C、设a=2x,b=3x,c=4x,
∵a2+b2=4x2+9x2=13x2,c2=16x2,a2+b2≠c2,
∴△ABC不是直角三角形,符合题意;
D、∵b2+c2=a2符合勾股定理逆定理,
∴△ABC是直角三角形,不符合题意.
故选:C.
3.
【分析】由矩形的性质和平行四边形的性质即可得出结论.
【解答】解:∵矩形的对边平行且相等,对角线互相平分且相等;
平行四边形的对边平行且相等,对角线互相平分;
∴矩形具有而平行四边形不具有的性质是对角线相等;
故选:A.
4.
【分析】由k=﹣2<0,b=4>0,可得图象经过一、二、四象限,y随x的增大而减小,再分别求解一次函数与坐标轴的交点坐标,从而可得答案.
【解答】解:∵y=﹣2x+4,k=﹣2<0,b=4>0,
∴图象经过一、二、四象限,y随x的增大而减小,
故A,B不符合题意;
当y=0时,﹣2x+4=0,解得x=2,
∴图象与x轴交于(2,0),故C符合题意;
当x=0时,y=4,
∴图象与y轴交于(0,4),故D不符合题意;
故选:C.
5.
【分析】根据中位线定理可得:AB=2DE.
【解答】解:∵D是AC的中点,E是BC的中点,
∴DE是△ABC的中位线,
∴,
∴AB=2DE,
故选:C.
6.
【分析】先根据勾股定理求出OP的长,由于OP=OA,故估算出OP的长,再根据点A在x轴的负半轴上即可得出结论.
【解答】解:∵点P坐标为(﹣2,3),
∴OP==,
∵点A、P均在以点O为圆心,以OP为半径的圆上,
∴OA=OP=,
∵9<13<16,
∴3<<4.
∵点A在x轴的负半轴上,
∴点A的横坐标介于﹣4和﹣3之间.
故选:C.
7.
【分析】此题有两个要求:①平均成绩较低,②状态稳定.于是应选平均数较小、方差较小的运动员参赛.
【解答】解:甲和丙的平均数较小,所以在甲和丙两人中选一人参加比赛,
由于甲的方差比丙小,所以甲更稳定,故选甲参加比赛.
故选:A.
8.
【分析】利用图象法画出平行四边形,可得结论.
【解答】解:如图平行四边形的第三个顶点坐标为(5,2),(﹣3,2),(3,﹣2).
故选:B.
9.
【分析】先利用直角三角形斜边上的中线性质可得CD=AD=BD=3,然后利用等腰三角形的三线合一性质可得ED⊥AD,从而在Rt△ADE中,利用勾股定理进行计算即可解答.
【解答】解:在Rt△ABC中,CD为斜边AB上的中线,
∴CD=AD=BD=AB=3,
∵AE=BE=7,
∴ED⊥AD,
在Rt△ADE中,DE===2,
故选:B.
10.
【分析】将点代入函数解析式,得到k=b,然后将不等式k(x﹣1)+b<0转化为函数y=kx+k<k的解集即可.
【解答】解:∵一次函数y=kx+b(k>0)的图象过点(﹣1,0),
∴0=﹣k+b,即k=b,
∴y=kx+k,
∴A(0,k)
∵k(x﹣1)+b<0,
∴kx﹣k+b<0,即kx+b<k,
∴kx+k<k,即求y=kx+k<k,
由图可知,kx+k<k的部分是点A的左侧部分,
∴k(x﹣1)+b<0的解集是x<0.
故选:C.
11.
【分析】根据函数图象中的数据,可以分别计算出两人的速度,从而可以判断各个选项中的说法是否正确,从而可以解答本题.
【解答】解:由图象可知,
两人出发1小时后相遇,故选项A正确,不符合题意;
嘉嘉跑步的速度为24÷3=8(km/h),故选项B正确,不符合题意;
琪琪的速度为:24÷1﹣8=16(km/h),
琪琪从开始至到达目的地用的时间为:24÷16=1.5(h),
∴琪琪到达目的地时两人相距8×1.5=12(km),故选项C错误,符合题意;
琪琪比嘉嘉提前3﹣1.5=1.5(h)到目的地,故选项D正确,不符合题意;
故选:C.
12.
【分析】根据正方形的性质,三角形全等的判定和性质,角的平分线的意义,点到直线的距离计算判断即可.
【解答】解:∵正方形ABCD,
∴AB=AD,∠BAE=∠ADF=90°,∠AEB+∠ABE=90°,
在△BAE和△ADF中,
,
∴△BAE≌△ADF(SAS),
∴∠DAF=∠ABE,
∴∠AEB+∠DAF=90°,
∴∠AGE=∠BGF=90°,
∴∠BGF是定值,
故①正确;
设FB平分∠AFC,
∵BG⊥AF,BC⊥CF,
∴BG=BC,AB>BG,
∵正方形ABCD,
∴AB=BC,
∴BG=BC,BC>BG,
矛盾,故假设不成立,
故②错误;
延长AF,交BC的延长线于点H,
根据(1)得,△BAE≌△ADF,∠BGF=90°,
∴AE=DF,
∵E是AD中点,
∴,
∵正方形ABCD,
∴AD=DC,
∴,
∴DF=FC;
∵正方形ABCD,
∴∠HCF=∠ADF=90°,
在△HCF和△ADF中,
,
∴△HCF≌△ADF(ASA),
∴AD=CH,
∴AD=CH=BC,
∴,
∴CG=AB,
故③正确;
过点G作QK⊥DC于点K,交AB于点Q,
∵正方形ABCD,
∴∠QAD=∠ADK=90°,
∴四边形AQKD是矩形,
∴QK=AD=4,QK⊥AB,
根据①得,△BAE≌△ADF,
∴S△BAE=S△ADF,
∴S△BAE﹣S△AGF=S△ADF﹣S△AGF,
∴S△BAG=S四边形DEGF=2,
∴,
∴,
解得QG=1,
∴GK=QK﹣QG=4﹣1=3,
故当四边形GEDF的面积是2时,点G到直线CD的距离为3,
故④正确,
故选:B.
二、填空题
13.
【分析】先利用完全平方公式对代数式变形,然后代值求解即可.
【解答】解:∵,
∴x2﹣2x+1=(x﹣1)2===2023,
故答案为:2023.
14.
【分析】连接AC,BD,根据正方形AECF的面积为50cm2,菱形ABCD的面积为120cm2,求出AC和BD,即可得出答案.
【解答】解:如图,连接AC,BD,
∵正方形AECF的面积为50cm2,
∴AC=×=10(cm),
∵菱形ABCD的面积为120cm2,
∴BD=2×120÷10=24(cm),
∴菱形ABCD的边长为=13(cm),
故答案为:13.
15.
【分析】由在直线y=kx+6上存在点Q,使得点Q是正方形OABC的“和谐点”,可知Q′在直线y=k(x+3)+8上,求得直线经过点A时的k的值,即可求得k的取值范围.
【解答】解:直线y=kx+6向上平移2个单位,再向左平移3个单位后得到y=k(x+3)+8,
把B(﹣4,4)代入得﹣k+8=4,解得k=4,
∴0<k≤4.
故答案为:0<k≤4.
16.
【分析】设全等的直角三角形的两条直角边为a、b且a>b,则,,,先证明,再证明即可得到答案.
【解答】解:设全等的直角三角形的两条直角边为a、b且a>b,
由题意可知:,,,
∵正方形EFGH的边长为2,
∴,
∴,
=a2+2ab+b2+a2+b2+a2﹣2ab+b2
=3(a2+b2)
=12,
故答案为:12.
三、解答题
17.解:(1)
=
=
=;
(2)
=
=
=.
18.解:设AB=AD=xcm,由题意得,CE=BF=6cm,
∴AC=AD+DE﹣CE=(x﹣2)cm,
∵AC2+BC2=AB2,
∴(x﹣2)2+82=x2,
∴x=17,
∴AD=17cm.
答:钟摆AD的长度.
19.解:(1)C所占的百分比是:×100%=30%,
a%=1﹣30%﹣20%﹣10%=40%,即a=40;
∵共有10个数,中位数是第5、第6个数的平均数,
∴中位数b==90.5;
∵99出现了3次,出现的次数最多,
∴众数c=99.
故答案为:40;90.5;99;
(2)我认为八年级成绩更好,理由如下:
因为两个年级的平均数相同,而八年级的成绩的众数大于七年级,方差小于七年级.
(3)根据题意得:
450×+500×(30%+40%)
=270+350
=620(人),
答:估计参加竞赛活动成绩优秀的学生人数是620人.
20.解:(1)四边形AECF是矩形,
理由:∵AB=CD,BC=AD,
∴四边形ABCD是平行四边形,
∴∠B=∠D,AD∥BC,
∵AE⊥BC、CF⊥AD,
∴∠AEB=∠CFD=90°,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∴AF=CE,
∵∠AEC=90°,
∴四边形AECF是矩形;
(2)∵∠AEB=90°,∠B=60°,AB=4,
∴∠BAE=30°,
∴,AE=AB=2,
∵点E是BC的中点,
∴BC=2BE=4,
∴四边形ABCD的面积=BC AE=4×=8.
21.解:(1)根据题意得,甲、乙两采摘园优惠前的草莓销售价格:300÷10=30(元/千克).
∴y甲=30×0.6x+60=18x+60;
当x≥10时,设y乙=kx+b,
由题意的:,
解得,
∴y乙=12x+180,
∴y乙与x之间的函数关系式为:yz=12x+180(x≥10);
(2)当x=15时,y甲=18×15+60=330,y乙=12×15+180=360,
∴y甲<y乙,
∴他在甲家草莓园采摘更划算.
22.解:(1),
故答案为:;
(2)原式=﹣1+﹣+﹣+…+﹣
=﹣1+﹣+﹣+﹣…﹣+
=
=﹣1+13
=12;
(3)∵,
∴a﹣2=,
∴(a﹣2)2=5,即a2﹣4a+4=5.
∴a2﹣4a=1.
∴a4﹣4a3﹣4a+3=a2(a2﹣4a)﹣4a+3=a2×1﹣4a+3=a2﹣4a+3=1+3=4.
23.解:(1)∵在△ABC中,∠ACB=90°,AB=5,BC=3,
∴由勾股定理得:,
∵已知点P从点A出发,以每秒2个单位长度的速度运动,
∴当点P在AC的延长线上时,点P运动的长度为:AC+CP=2t,
∵AC=4,
∴CP=2t﹣AC=2t﹣4.
故答案为:2t﹣4.
(2)过点P作PM⊥AB于点M,如图所示:
∵∠ACB=90°,
∴PC⊥BC,
∵点P在∠ABC的角平分线上,PM⊥AB,
∴PC=PM,
又∵PB=PB,
∴Rt△PCB≌Rt△PMB(HL),
∴CB=MB,
∴AM=AB﹣MB=AB=BC=5﹣3=2,
设PM=PC=x,则AP=4﹣x,
在Rt△APM中,AM2+PM2=AP2,
∴22+x2=(4﹣x)2,
解得:,
,
即若点P在∠ABC的角平分线上,则t的值为.
(3)当AB作为底边时,如图所示:
则PA=PB,设PA=a,则PC=AC﹣AP=4﹣a,
在Rt△PCB中,PB2=PC2+CB2,
a2=(4﹣a)2+32,
解得:,
此时;
当AB作为腰时,如图所示:
AP1=AB=5,此时;
AB=BP2时,
∵BC⊥AP2,
∴AP2=2AC=8,
此时t=8÷2=4,
综上分析可知,t的值为或或4.
24.解:(1)当t=3时,则点P(0,7),
则直线l的表达式为:y=﹣x+7,
故答案为:y=﹣x+7;
(2)将点M、N的坐标分别代入y=﹣x+b得:
3=﹣4+b,5=﹣5+b,
则b=7,b=10,
则运动的距离分别为:6,9,
则3≤t≤4.5;
(3)作M点关于l的对称点M',如图所示:
连接MM'与x轴交于点F,直线l与x轴交于E点,直线l与MM'交于点H,
则有MM'⊥HE,
∴∠EHF=90°,
∵直线l与x轴所夹的锐角为45°,
∴∠MFE=90°﹣45°=45°,
∴直线MM'解析式中的k=1,设MM'解析式为y=x+n,
代入点M(4,3),解得n=﹣1,
故直线MM'的解析式为:y=x﹣1,
∴设点M'的坐标为(a,a﹣1),
由H是M和M'的中点可知:
H点坐标为(,),即H(a+2,a+1),
情况一:当M'位于x轴上时,即a﹣1=0,即a=1时,
求得H点坐标为(2.5,1.5),
又H点在直线l上,故将H点坐标代入直线l的解析式y=﹣x+b中,
求得b=4,此时l的解析式y=﹣x+4,
∴此时P点坐标为(0,4),
故时间t=(4﹣1)÷2=1.5秒;
情况二:当M'位于y轴上时,即a=0时,
求得H点坐标为(2,1),
又H点在直线l上,故将H点坐标代入直线l的解析式y=﹣x+b中,
求得b=3,此时ll的解析式y=﹣x+3,
∴此时P点坐标为(0,3),
故时间t=(3﹣1)÷2=1秒;
∴t=1.5秒或1秒时,点M关于l的对称点落在坐标轴上.
25.证明:(1)点拨:如图2,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连接EM,
易证△ABM≌△EBM(SAS),
∴AM=EM,∠1=∠2;
∵AM=MN,
∴EM=MN,
∴∠3=∠4;
∵∠3+∠1=∠4+∠5=60°,
∴∠1=∠2=∠5.
∵∠2+∠6=120,
∴∠5+∠6=120°,
∴∠AMN=60°;
(2)拓展:延长AB至E,使EB=AB,连接EMC、EC,如图所示:
则EB=BC,∠EBM中=90°=∠ABM,
∴△EBC是等腰直角三角形,
∴∠BEC=∠BCE=45°,
∵N是正方形ABCD的外角∠DCH的平分线上一点,
∴∠MCN=90°+45°=135°,
∴∠BCE+∠MCN=180°,
∴E、C、N,三点共线,
在△ABM和△EBM中,
,
∴△ABM≌△EBM(SAS),
∴AM=EM,∠1=∠2,
∵AM=MN,
∴EM=MN,
∴∠3=∠4,
∵∠2+∠3=45°,∠4+∠5=45°,
∴∠1=∠2=∠5,
∵∠1+∠6=90°,
∴∠5+∠6=90°,
∴∠AMN=180°﹣90°=90°.
同课章节目录
