17.1 勾股定理 教学设计(表格式) 人教版(2024)数学八年级下册
文档属性
| 名称 | 17.1 勾股定理 教学设计(表格式) 人教版(2024)数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 249.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-04 12:31:34 | ||
图片预览

文档简介
17.1 勾股定理
课题
勾股定理
教材分析
勾股定理是直角三角形的一条非常重要的性质,它将数与形密切地联系起来,揭示了一个直角三角形三边之间的数量关系,是后续学习解直角三角形的基础,是三角形知识的深化。
学情分析
八年级学生好奇心强,学生对几何图形的观察,几何图形的分析能力已初步形成。本节内容思维量较大,对思维的严谨、归纳推理等能力有较高要求,学生学习起来有一定难度。
教学目标
1.掌握勾股定理,会运用勾股定理解释简单的几何问题;
2.经历勾股定理的证明过程,体会数形结合的数学思想;
3.通过对我国古代研究勾股定理成就的介绍,培养民族自豪感;
4.通过对勾股定理的探索和交流,培养数学学习的自信心。
重点难点
重点:掌握勾股定理,并会运用勾股定理解决一些几何问题。
难点:用拼图的方法验证勾股定理。
教法学法
讲授法、讨论法
教学过程设计
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 【情境引入】 教师活动:教师描述情境,并提出问题引发学生思考,引出本节课要讲解的内容。 相传在2500多年以前,毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面图案反映了直角三角形的某种数量关系。 观察一下,你能从中发现什么数量关系吗 认真观察,自主思考 通过情境引入,激发学生的探索兴趣和求知欲望
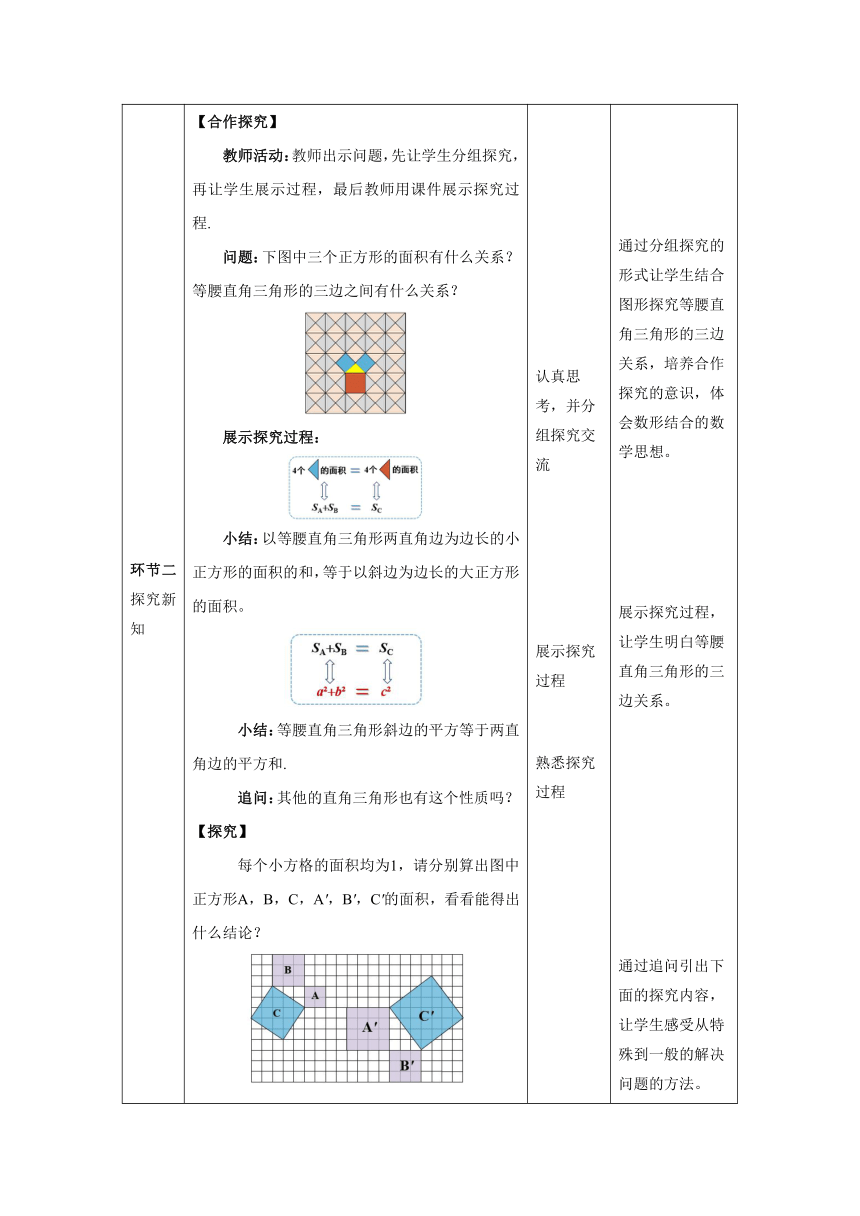
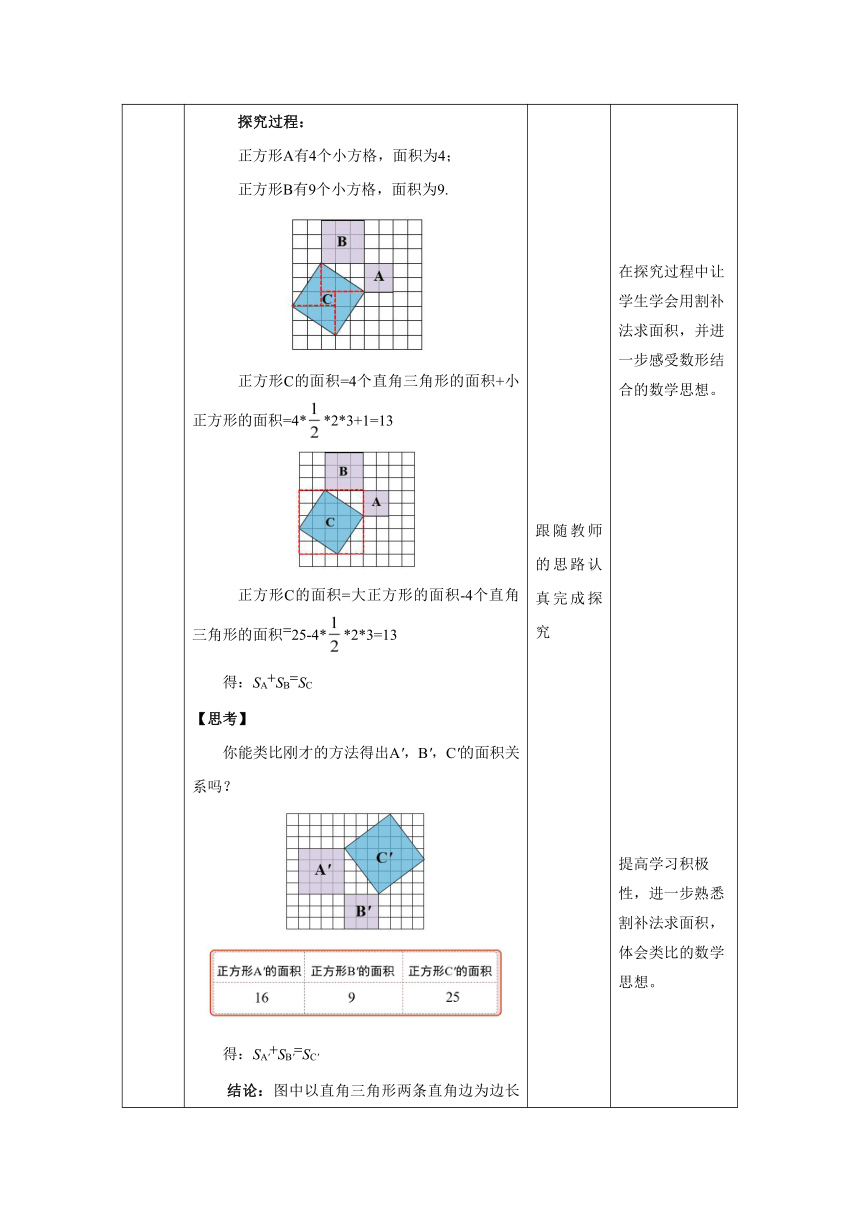
环节二 探究新知 【合作探究】 教师活动:教师出示问题,先让学生分组探究,再让学生展示过程,最后教师用课件展示探究过程. 问题:下图中三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系? 展示探究过程: 小结:以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积。 小结:等腰直角三角形斜边的平方等于两直角边的平方和. 追问:其他的直角三角形也有这个性质吗? 【探究】 每个小方格的面积均为1,请分别算出图中正方形A,B,C,A',B',C'的面积,看看能得出什么结论? 探究过程: 正方形A有4个小方格,面积为4; 正方形B有9个小方格,面积为9. 正方形C的面积=4个直角三角形的面积+小正方形的面积=4**2*3+1=13 正方形C的面积=大正方形的面积-4个直角三角形的面积25-4**2*3=13 得:SASBSC 【思考】 你能类比刚才的方法得出A',B',C'的面积关系吗? 得:SA'SB'SC' 结论:图中以直角三角形两条直角边为边长的正方形的面积的和,等于以直角三角形的斜边为边长的正方形的面积,即直角三角形两直角边的平方和等于斜边的平方。 猜想:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a b c 。 【探究】 教师活动:先让学生分组探究,剪一剪、拼一拼,并展示剪拼过程,然后播放动画,看剪拼过程是否一样(可有多种剪拼过程,课件展示其中一种),并验证刚才的猜想。 以直角三角形的两条直角边a、b为边作两个正方形,把两个正方形如图1连在一起,通过剪、拼把它拼成图2的样子,动手试一试,并证明刚刚的猜想。 追问1:如何计算大正方形的面积? 追问2:通过动手操作和仔细计算,你能得到什么结论? 追问3:你还知道其他的证明猜想的方法吗? 【归纳】 勾股定理: 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a b c . 注意:在西方,又称为“毕达哥拉斯定理”. 科普小知识 在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 【延伸】 如图1,这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自相乘为中黄实.加差实,亦成弦实。 这个图片被选为2002年在北京召开的国际数学大会的会徽。 认真思考,并分组探究交流 展示探究过程 熟悉探究过程 跟随教师的思路认真完成探究 认真思考并计算 学生提出猜想 认真思考,积极动手剪拼 熟悉勾股定理 通过分组探究的形式让学生结合图形探究等腰直角三角形的三边关系,培养合作探究的意识,体会数形结合的数学思想。 展示探究过程,让学生明白等腰直角三角形的三边关系。 通过追问引出下面的探究内容,让学生感受从特殊到一般的解决问题的方法。 在探究过程中让学生学会用割补法求面积,并进一步感受数形结合的数学思想。 提高学习积极性,进一步熟悉割补法求面积,体会类比的数学思想。 通过猜想培养学生归纳总结的能力。 通过剪一剪、拼一拼充分调动学生的思维,进一步激发求知欲,培养学生的动手能力和分析问题、解决问题的能力。 通过归纳让学生熟悉勾股定理,并了解勾股定理的相关背景知识。 让学生熟悉我国古代数学家在勾股定理上的成就,增强民族自豪感。
环节三 应用新知 【典型例题】 【例1】求出图中字母所代表的正方形的面积。 解:(1) SA22514481; (2) SA802456;SB245680。 【例2】设直角三角形的两条直角边长分别为a和b,斜边长为c。 (1) 已知a=5,b=12,求c; (2) 已知a=6,c=10,求b; (3) 已知c=25,b=15,求a. 解:(1) ; (2) ; (3) . 明确例题的做法 让学生在探究过程中进一步加深对勾股定理的认识和理解,培养学生的应用意识。
环节四 巩固新知 【随堂练习】 1.求下列图中表示边长的未知数x、y、z的值。 2.(1)直角△ABC的两条直角边a=12,b=16,斜边c=______. (2)直角△ABC的一条直角边a=10,斜边c=26,则b=______. 3.已知:Rt△ABC中,AB=4,AC=3,则BC= . 答案: 1.解:(1) x15;(2) y5 ;(3) z7. 2.解:(1) 20;(2) 24. 3.解:5或. 自主完成练习,然后集体交流评价。 通过课堂练习及时巩固本节课所学内容,并考查学生的知识应用能力,培养独立完成练习的习惯。
环节五 课堂小结 回顾本节课所讲的内容 通过小结总结回顾本节课学习内容,帮助学生归纳、巩固所学知识。
课题
勾股定理
教材分析
勾股定理是直角三角形的一条非常重要的性质,它将数与形密切地联系起来,揭示了一个直角三角形三边之间的数量关系,是后续学习解直角三角形的基础,是三角形知识的深化。
学情分析
八年级学生好奇心强,学生对几何图形的观察,几何图形的分析能力已初步形成。本节内容思维量较大,对思维的严谨、归纳推理等能力有较高要求,学生学习起来有一定难度。
教学目标
1.掌握勾股定理,会运用勾股定理解释简单的几何问题;
2.经历勾股定理的证明过程,体会数形结合的数学思想;
3.通过对我国古代研究勾股定理成就的介绍,培养民族自豪感;
4.通过对勾股定理的探索和交流,培养数学学习的自信心。
重点难点
重点:掌握勾股定理,并会运用勾股定理解决一些几何问题。
难点:用拼图的方法验证勾股定理。
教法学法
讲授法、讨论法
教学过程设计
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 【情境引入】 教师活动:教师描述情境,并提出问题引发学生思考,引出本节课要讲解的内容。 相传在2500多年以前,毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面图案反映了直角三角形的某种数量关系。 观察一下,你能从中发现什么数量关系吗 认真观察,自主思考 通过情境引入,激发学生的探索兴趣和求知欲望
环节二 探究新知 【合作探究】 教师活动:教师出示问题,先让学生分组探究,再让学生展示过程,最后教师用课件展示探究过程. 问题:下图中三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系? 展示探究过程: 小结:以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积。 小结:等腰直角三角形斜边的平方等于两直角边的平方和. 追问:其他的直角三角形也有这个性质吗? 【探究】 每个小方格的面积均为1,请分别算出图中正方形A,B,C,A',B',C'的面积,看看能得出什么结论? 探究过程: 正方形A有4个小方格,面积为4; 正方形B有9个小方格,面积为9. 正方形C的面积=4个直角三角形的面积+小正方形的面积=4**2*3+1=13 正方形C的面积=大正方形的面积-4个直角三角形的面积25-4**2*3=13 得:SASBSC 【思考】 你能类比刚才的方法得出A',B',C'的面积关系吗? 得:SA'SB'SC' 结论:图中以直角三角形两条直角边为边长的正方形的面积的和,等于以直角三角形的斜边为边长的正方形的面积,即直角三角形两直角边的平方和等于斜边的平方。 猜想:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a b c 。 【探究】 教师活动:先让学生分组探究,剪一剪、拼一拼,并展示剪拼过程,然后播放动画,看剪拼过程是否一样(可有多种剪拼过程,课件展示其中一种),并验证刚才的猜想。 以直角三角形的两条直角边a、b为边作两个正方形,把两个正方形如图1连在一起,通过剪、拼把它拼成图2的样子,动手试一试,并证明刚刚的猜想。 追问1:如何计算大正方形的面积? 追问2:通过动手操作和仔细计算,你能得到什么结论? 追问3:你还知道其他的证明猜想的方法吗? 【归纳】 勾股定理: 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a b c . 注意:在西方,又称为“毕达哥拉斯定理”. 科普小知识 在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 【延伸】 如图1,这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自相乘为中黄实.加差实,亦成弦实。 这个图片被选为2002年在北京召开的国际数学大会的会徽。 认真思考,并分组探究交流 展示探究过程 熟悉探究过程 跟随教师的思路认真完成探究 认真思考并计算 学生提出猜想 认真思考,积极动手剪拼 熟悉勾股定理 通过分组探究的形式让学生结合图形探究等腰直角三角形的三边关系,培养合作探究的意识,体会数形结合的数学思想。 展示探究过程,让学生明白等腰直角三角形的三边关系。 通过追问引出下面的探究内容,让学生感受从特殊到一般的解决问题的方法。 在探究过程中让学生学会用割补法求面积,并进一步感受数形结合的数学思想。 提高学习积极性,进一步熟悉割补法求面积,体会类比的数学思想。 通过猜想培养学生归纳总结的能力。 通过剪一剪、拼一拼充分调动学生的思维,进一步激发求知欲,培养学生的动手能力和分析问题、解决问题的能力。 通过归纳让学生熟悉勾股定理,并了解勾股定理的相关背景知识。 让学生熟悉我国古代数学家在勾股定理上的成就,增强民族自豪感。
环节三 应用新知 【典型例题】 【例1】求出图中字母所代表的正方形的面积。 解:(1) SA22514481; (2) SA802456;SB245680。 【例2】设直角三角形的两条直角边长分别为a和b,斜边长为c。 (1) 已知a=5,b=12,求c; (2) 已知a=6,c=10,求b; (3) 已知c=25,b=15,求a. 解:(1) ; (2) ; (3) . 明确例题的做法 让学生在探究过程中进一步加深对勾股定理的认识和理解,培养学生的应用意识。
环节四 巩固新知 【随堂练习】 1.求下列图中表示边长的未知数x、y、z的值。 2.(1)直角△ABC的两条直角边a=12,b=16,斜边c=______. (2)直角△ABC的一条直角边a=10,斜边c=26,则b=______. 3.已知:Rt△ABC中,AB=4,AC=3,则BC= . 答案: 1.解:(1) x15;(2) y5 ;(3) z7. 2.解:(1) 20;(2) 24. 3.解:5或. 自主完成练习,然后集体交流评价。 通过课堂练习及时巩固本节课所学内容,并考查学生的知识应用能力,培养独立完成练习的习惯。
环节五 课堂小结 回顾本节课所讲的内容 通过小结总结回顾本节课学习内容,帮助学生归纳、巩固所学知识。
