江苏省苏州市振华、景范、叶圣陶学校2024-2025学年七年级(上)期末数学试卷(含解析)
文档属性
| 名称 | 江苏省苏州市振华、景范、叶圣陶学校2024-2025学年七年级(上)期末数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 501.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-04 10:39:10 | ||
图片预览




文档简介
江苏省苏州市振华、景范、叶圣陶学校2024-2025学年七年级(上)期末数学试卷
一、本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的相反数是( )
A. B. C. D.
2.下列运算中,正确的是( )
A. B.
C. D.
3.下列等式变形中,错误的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
4.为贯彻落实党中央国务院关于促消费和惠民生有关要求,进一步提振消费,江苏省有关部门发布了相关数码产品补贴专项活动.从年月日至月日,凡购买手机、平板电脑、智能手表等数码产品,可享受的补贴,即优惠若标价为元的某品牌手机参与本次补贴专项活动,则顾客购买一部此品牌手机实际支付的费用为( )
A. 元 B. 元 C. 元 D. 元
5.如图,,,则的度数为( )
A. B. C. D.
6.如图,是直线上一点,将直角三角板的直角顶点放在点处点,分别在异侧,射线平分若,则的度数为( )
A. B. C. D.
7.九章算术被誉为人类科学史上应用数学的“算经之首”,其中有一题为“今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲乃发长安,问凡何日相逢?“其大意如下:甲从长安出发,用天时间可到达齐国;乙从齐国出发,用天时间可到达长安.若乙先从齐国出发天,甲才从长安出发,问甲经过多少天与乙相遇?设甲经过天后与乙相遇,则下列方程正确的是( )
A. B.
C. D.
8.方胜纹是以几个菱形压角相叠而构成的几何图形注:四条边都相等的四边形是菱形,是中国传统吉祥装饰纹样中一种独具特色的几何纹样.苏州拙政园远香堂方形窗棂上就装饰有这种纹样.如图,第一个图案中有个菱形,第二个图案中有个菱形,第三个图案中有个菱形,,按照这样的方法排列下去,若第个图案中有个菱形,则的值是( )
A. B. C. D.
二、本题共8小题,每小题3分,共24分。
9.苏州地铁号线于年月日正式开通运营,全长米,途径相城区、工业园区、吴中区,是古城东侧重要的客流通道.数据用科学记数法可表示为 .
10.已知,则的补角的度数为 .
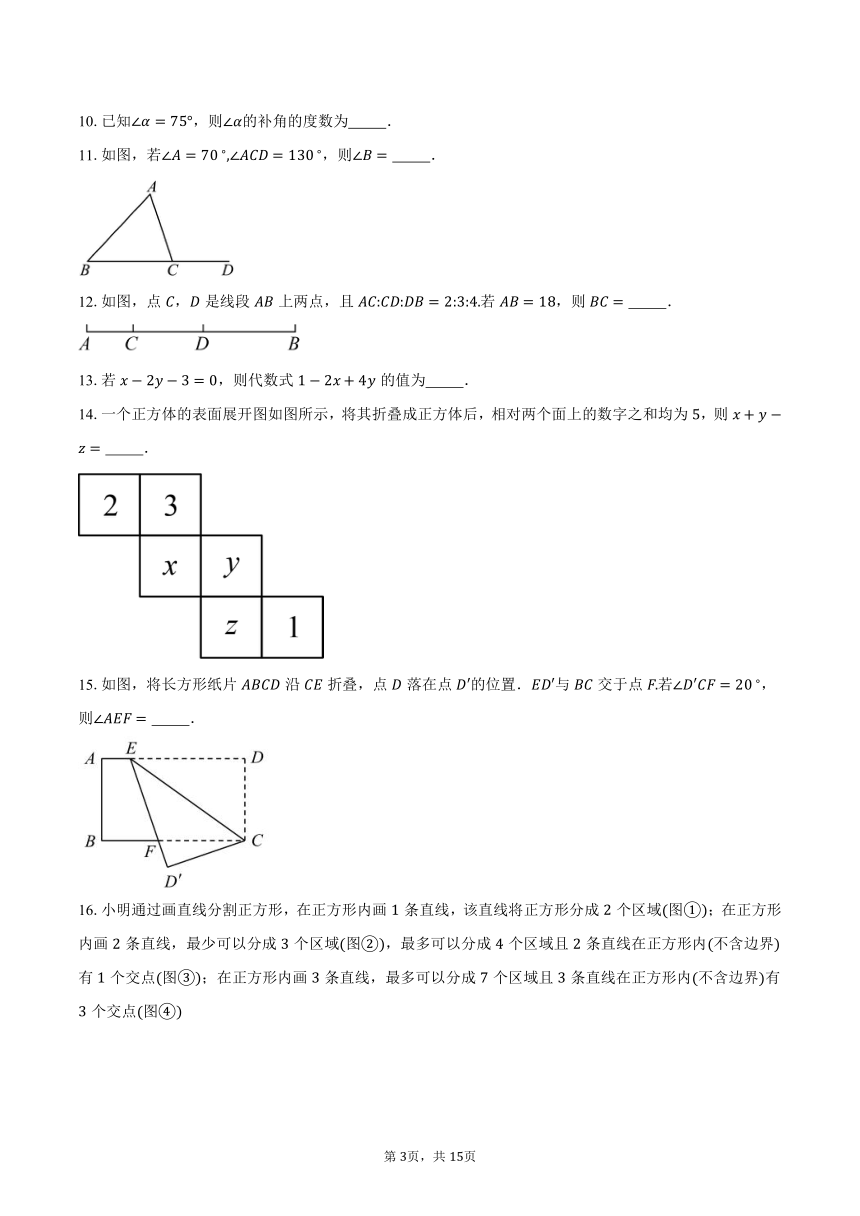
11.如图,若,则 .
12.如图,点,是线段上两点,且若,则 .
13.若,则代数式的值为 .
14.一个正方体的表面展开图如图所示,将其折叠成正方体后,相对两个面上的数字之和均为,则 .
15.如图,将长方形纸片沿折叠,点落在点的位置.与交于点若,则 .
16.小明通过画直线分割正方形,在正方形内画条直线,该直线将正方形分成个区域图;在正方形内画条直线,最少可以分成个区域图,最多可以分成个区域且条直线在正方形内不含边界有个交点图;在正方形内画条直线,最多可以分成个区域且条直线在正方形内不含边界有个交点图
小明又进行了多次试验,其中次他在正方形内画条直线,将正方形分成个区域且条直线在正方形内不含边界有个交点,则,,之间的数量关系为 .
三、本大题共2小题,共12分。
17.计算:.
18.先化简,再求值:,其中.
四、本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
19.解方程:.
20.如图,.
填空:
因为,
所以
因为,
所以 等量代换.
所以
若,求的度数.
21.如图,方格纸中的每个小正方形的边长为,点,,均为格点方格纸中小正方形的顶点
按下列要求画图:
标出格点,使,并画出直线;
标出格点,使,并画出直线.
计算的面积.
22.已知关于的方程的解与的解相同,求的值.
23.如图,直线交于点,,垂足为,.
求的度数;
若平分,求的度数.
24.已知线段,是射线上一点,是线段的中点.若,求线段的长.
25.某市对居民生活用水实行阶梯水价,每年收费标准如下表:
阶梯 家庭每年用水量 水价元立方米
第一阶梯 不超过立方米的部分
第二阶梯 超过立方米但不超过立方米的部分
第三阶梯 超过立方米的部分
已知小明家年共用水立方米,处于第一阶梯,共交水费元;小丽家年共用水立方米,处于第二阶梯,共交水费元.
填空: , ;
年小慧家共交水费元,求小慧家年的用水量.
26.
【数学魔术】魔术师请观众在心中想好一个数,然后将这个数按以下步骤计算,最后将计算结果告诉魔术师,魔术师能立刻说出观众想的那个数.
如果小明想的数是,那么他告诉魔术师的数是 ;
如果小明告诉魔术师的数是,那么他想的数是 .
【魔术创新】小明对数学魔术很感兴趣,他对小丽说:“请你任意想一个两位数,把这个两位数的十位数字先乘,再加,然后把所得的和乘,最后加上个位数字,所得的结果告诉我,我就能准确说出你想的那个数.“请用代数式的有关知识解释此魔术的奥秘
27.
【原理探究】如图,根据光的反射原理,反射角等于入射角,即反射光线与法线的夹角等于入射光线与法线的夹角法线为经过入射点且与平面镜垂直的直线,由此可得,理由为 .
【实际应用】
请用【原理探究】获得的结论解决以下问题:
如图,平面镜相对放置,光线经过两次反射,为反射光线.
若平面镜互相平行,那么入射光线与反射光线平行吗?为什么?
若,调整平面镜的位置,使得,请在备用图中画出相应的平面镜和反射光线,并求此时的度数.
答案和解析
1.
【解析】 的相反数是,
故选:.
2.
【解析】、,原计算错误,不符合题意;
B、,不是同类项,不能合并,不符合题意;
C、,原计算错误,不符合题意;
D、,计算正确,符合题意,
故选:.
3.
【解析】若,等式两边同时减去,则,即,故选项 A正确,不符合题意;
B.若,等式两边同时乘以,的,故选项 B正确,不符合题意;
C.若,等式两边同时除以,则,故选项 C错误,符合题意;
D.若,等式两边同时除以,得,故选项 D正确,不符合题意.
故选:
4.
【解析】标价为元的某品牌手机实际支付的费用为元.
故选:.
5.
【解析】如图,,
,
,
.
故选:.
6.
【解析】设,则,,,,
,
,
,
,
解得:,
,
,
故选:.
7.
【解析】设甲经过天后与乙相遇,
根据题意得:,
故选D.
8.
【解析】由所给图形可知,
第个图案中菱形的个数为:;
第个图案中菱形的个数为:;
第个图案中菱形的个数为:;
,
所以第个图案中菱形的个数为个.
令,
解得,
即第个图案中菱形的个数为个.
故选:.
9.
【解析】数据用科学记数法可表示为,
故答案为:.
10.
【解析】,
的补角.
故答案为:.
11.度
【解析】是的一个外角,
,
,
,
.
故答案为:.
12.
【解析】若,
,
故答案为:.
13.
【解析】,
,
.
故答案为:.
14.
【解析】由正方体表面展开图的“相间、端是对面”可知,
“”与“”,“”与“”,“”与“”是对面,
又相对两个面上的数字之和均为,
,,,
.
故答案为:.
15. 度
【解析】四边形是长方形,
,
由折叠的性质得到:,
,
,
,
,
,
.
故答案为:.
16.
【解析】由图可知:
当画条直线时:直线数为,最多区域数为,交点数为,
当画条直线时:直线数为,最多区域数为,交点数为,
当画条直线时:直线数为,最多区域数为,交点数为,
,
当画条直线时:直线数为,最多区域数为,交点数为,
,
故答案为:.
17.【解析】
.
18.【解析】
,
当其中,时,
原式.
19.【解析】,
去分母,得,
去括号,得,
移项、合并同类项,得,
将系数化为,得.
20.【】【解析】
因为,
所以两直线平行,同位角相等.
因为,
所以等量代换.
所以内错角相等,两直线平行.
故答案为:两直线平行,同位角相等;;内错角相等,两直线平行;
【】【解析】
,
,
,
,
.
21.【】【解析】如图:直线即为所求;
如图:直线即为所求.
【】【解析】的面积为:.
22.解:,
去括号得:,
移项合并同类项得:,
将代入,
得:,
去分母得:,
去括号得:,
移项合并同类项得:,
系数化为得:.
23.【】【解析】,
,
,
;
【】【解析】直线交于点,,
,
平分,
,
,
.
24.【解析】当点在点的左侧时,如图
是线段的中点.若,
,
;
当点在点的右侧时,如图,
是线段的中点.若,
,
;
综上所述或.
25.【】【解析】
由用水立方米,处于第一阶梯,共交水费元,得,求得;而用水立方米,处于第二阶梯,共交水费元,据此列方程,求得,于是得到问题的答案;
解:小明家年共用水立方米,处于第一阶梯,共交水费元,
,
解得,
第一阶梯的水价为元立方米,
小丽家年共用水立方米,处于第二阶梯,共交水费元,
,
解得,
故答案为:,;
【】【解析】设小慧家年的用水量为立方米,
元,
用水立方米时,水费为元,
年小慧家共交水费元,且元元,
小慧家年的用水量超过立方米,
根据题意得,
解得,
答:小慧家年的用水量为立方米.
26.【】
【解析】如果小明想的数是,
那么他告诉魔术师的数是
;
如果小明告诉魔术师的数是,
那么他想的数是
;
故答案为:、;
【】【解析】设这个两位数为,
由题意知,,
即将所得结果减去即为原数.
27.【】
反射角等于入射角,,
等角的余角相等,
故答案为:等角的余角相等;
【】【解析】入射光线与反射光线平行,
理由:由平面镜原理得:,
,
,
,
,
;
【】【解析】平面镜和反射光线如下图和图所示:
当反射光线向右时:延长到,
,
由平面镜原理得:,
,
,
,
当和互换位置时,;
当反射光线向左时:如下图所示:
,
,
由平面镜原理得:,平分,,
,
,
当和互换位置时,.
第1页,共1页
一、本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的相反数是( )
A. B. C. D.
2.下列运算中,正确的是( )
A. B.
C. D.
3.下列等式变形中,错误的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
4.为贯彻落实党中央国务院关于促消费和惠民生有关要求,进一步提振消费,江苏省有关部门发布了相关数码产品补贴专项活动.从年月日至月日,凡购买手机、平板电脑、智能手表等数码产品,可享受的补贴,即优惠若标价为元的某品牌手机参与本次补贴专项活动,则顾客购买一部此品牌手机实际支付的费用为( )
A. 元 B. 元 C. 元 D. 元
5.如图,,,则的度数为( )
A. B. C. D.
6.如图,是直线上一点,将直角三角板的直角顶点放在点处点,分别在异侧,射线平分若,则的度数为( )
A. B. C. D.
7.九章算术被誉为人类科学史上应用数学的“算经之首”,其中有一题为“今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲乃发长安,问凡何日相逢?“其大意如下:甲从长安出发,用天时间可到达齐国;乙从齐国出发,用天时间可到达长安.若乙先从齐国出发天,甲才从长安出发,问甲经过多少天与乙相遇?设甲经过天后与乙相遇,则下列方程正确的是( )
A. B.
C. D.
8.方胜纹是以几个菱形压角相叠而构成的几何图形注:四条边都相等的四边形是菱形,是中国传统吉祥装饰纹样中一种独具特色的几何纹样.苏州拙政园远香堂方形窗棂上就装饰有这种纹样.如图,第一个图案中有个菱形,第二个图案中有个菱形,第三个图案中有个菱形,,按照这样的方法排列下去,若第个图案中有个菱形,则的值是( )
A. B. C. D.
二、本题共8小题,每小题3分,共24分。
9.苏州地铁号线于年月日正式开通运营,全长米,途径相城区、工业园区、吴中区,是古城东侧重要的客流通道.数据用科学记数法可表示为 .
10.已知,则的补角的度数为 .
11.如图,若,则 .
12.如图,点,是线段上两点,且若,则 .
13.若,则代数式的值为 .
14.一个正方体的表面展开图如图所示,将其折叠成正方体后,相对两个面上的数字之和均为,则 .
15.如图,将长方形纸片沿折叠,点落在点的位置.与交于点若,则 .
16.小明通过画直线分割正方形,在正方形内画条直线,该直线将正方形分成个区域图;在正方形内画条直线,最少可以分成个区域图,最多可以分成个区域且条直线在正方形内不含边界有个交点图;在正方形内画条直线,最多可以分成个区域且条直线在正方形内不含边界有个交点图
小明又进行了多次试验,其中次他在正方形内画条直线,将正方形分成个区域且条直线在正方形内不含边界有个交点,则,,之间的数量关系为 .
三、本大题共2小题,共12分。
17.计算:.
18.先化简,再求值:,其中.
四、本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
19.解方程:.
20.如图,.
填空:
因为,
所以
因为,
所以 等量代换.
所以
若,求的度数.
21.如图,方格纸中的每个小正方形的边长为,点,,均为格点方格纸中小正方形的顶点
按下列要求画图:
标出格点,使,并画出直线;
标出格点,使,并画出直线.
计算的面积.
22.已知关于的方程的解与的解相同,求的值.
23.如图,直线交于点,,垂足为,.
求的度数;
若平分,求的度数.
24.已知线段,是射线上一点,是线段的中点.若,求线段的长.
25.某市对居民生活用水实行阶梯水价,每年收费标准如下表:
阶梯 家庭每年用水量 水价元立方米
第一阶梯 不超过立方米的部分
第二阶梯 超过立方米但不超过立方米的部分
第三阶梯 超过立方米的部分
已知小明家年共用水立方米,处于第一阶梯,共交水费元;小丽家年共用水立方米,处于第二阶梯,共交水费元.
填空: , ;
年小慧家共交水费元,求小慧家年的用水量.
26.
【数学魔术】魔术师请观众在心中想好一个数,然后将这个数按以下步骤计算,最后将计算结果告诉魔术师,魔术师能立刻说出观众想的那个数.
如果小明想的数是,那么他告诉魔术师的数是 ;
如果小明告诉魔术师的数是,那么他想的数是 .
【魔术创新】小明对数学魔术很感兴趣,他对小丽说:“请你任意想一个两位数,把这个两位数的十位数字先乘,再加,然后把所得的和乘,最后加上个位数字,所得的结果告诉我,我就能准确说出你想的那个数.“请用代数式的有关知识解释此魔术的奥秘
27.
【原理探究】如图,根据光的反射原理,反射角等于入射角,即反射光线与法线的夹角等于入射光线与法线的夹角法线为经过入射点且与平面镜垂直的直线,由此可得,理由为 .
【实际应用】
请用【原理探究】获得的结论解决以下问题:
如图,平面镜相对放置,光线经过两次反射,为反射光线.
若平面镜互相平行,那么入射光线与反射光线平行吗?为什么?
若,调整平面镜的位置,使得,请在备用图中画出相应的平面镜和反射光线,并求此时的度数.
答案和解析
1.
【解析】 的相反数是,
故选:.
2.
【解析】、,原计算错误,不符合题意;
B、,不是同类项,不能合并,不符合题意;
C、,原计算错误,不符合题意;
D、,计算正确,符合题意,
故选:.
3.
【解析】若,等式两边同时减去,则,即,故选项 A正确,不符合题意;
B.若,等式两边同时乘以,的,故选项 B正确,不符合题意;
C.若,等式两边同时除以,则,故选项 C错误,符合题意;
D.若,等式两边同时除以,得,故选项 D正确,不符合题意.
故选:
4.
【解析】标价为元的某品牌手机实际支付的费用为元.
故选:.
5.
【解析】如图,,
,
,
.
故选:.
6.
【解析】设,则,,,,
,
,
,
,
解得:,
,
,
故选:.
7.
【解析】设甲经过天后与乙相遇,
根据题意得:,
故选D.
8.
【解析】由所给图形可知,
第个图案中菱形的个数为:;
第个图案中菱形的个数为:;
第个图案中菱形的个数为:;
,
所以第个图案中菱形的个数为个.
令,
解得,
即第个图案中菱形的个数为个.
故选:.
9.
【解析】数据用科学记数法可表示为,
故答案为:.
10.
【解析】,
的补角.
故答案为:.
11.度
【解析】是的一个外角,
,
,
,
.
故答案为:.
12.
【解析】若,
,
故答案为:.
13.
【解析】,
,
.
故答案为:.
14.
【解析】由正方体表面展开图的“相间、端是对面”可知,
“”与“”,“”与“”,“”与“”是对面,
又相对两个面上的数字之和均为,
,,,
.
故答案为:.
15. 度
【解析】四边形是长方形,
,
由折叠的性质得到:,
,
,
,
,
,
.
故答案为:.
16.
【解析】由图可知:
当画条直线时:直线数为,最多区域数为,交点数为,
当画条直线时:直线数为,最多区域数为,交点数为,
当画条直线时:直线数为,最多区域数为,交点数为,
,
当画条直线时:直线数为,最多区域数为,交点数为,
,
故答案为:.
17.【解析】
.
18.【解析】
,
当其中,时,
原式.
19.【解析】,
去分母,得,
去括号,得,
移项、合并同类项,得,
将系数化为,得.
20.【】【解析】
因为,
所以两直线平行,同位角相等.
因为,
所以等量代换.
所以内错角相等,两直线平行.
故答案为:两直线平行,同位角相等;;内错角相等,两直线平行;
【】【解析】
,
,
,
,
.
21.【】【解析】如图:直线即为所求;
如图:直线即为所求.
【】【解析】的面积为:.
22.解:,
去括号得:,
移项合并同类项得:,
将代入,
得:,
去分母得:,
去括号得:,
移项合并同类项得:,
系数化为得:.
23.【】【解析】,
,
,
;
【】【解析】直线交于点,,
,
平分,
,
,
.
24.【解析】当点在点的左侧时,如图
是线段的中点.若,
,
;
当点在点的右侧时,如图,
是线段的中点.若,
,
;
综上所述或.
25.【】【解析】
由用水立方米,处于第一阶梯,共交水费元,得,求得;而用水立方米,处于第二阶梯,共交水费元,据此列方程,求得,于是得到问题的答案;
解:小明家年共用水立方米,处于第一阶梯,共交水费元,
,
解得,
第一阶梯的水价为元立方米,
小丽家年共用水立方米,处于第二阶梯,共交水费元,
,
解得,
故答案为:,;
【】【解析】设小慧家年的用水量为立方米,
元,
用水立方米时,水费为元,
年小慧家共交水费元,且元元,
小慧家年的用水量超过立方米,
根据题意得,
解得,
答:小慧家年的用水量为立方米.
26.【】
【解析】如果小明想的数是,
那么他告诉魔术师的数是
;
如果小明告诉魔术师的数是,
那么他想的数是
;
故答案为:、;
【】【解析】设这个两位数为,
由题意知,,
即将所得结果减去即为原数.
27.【】
反射角等于入射角,,
等角的余角相等,
故答案为:等角的余角相等;
【】【解析】入射光线与反射光线平行,
理由:由平面镜原理得:,
,
,
,
,
;
【】【解析】平面镜和反射光线如下图和图所示:
当反射光线向右时:延长到,
,
由平面镜原理得:,
,
,
,
当和互换位置时,;
当反射光线向左时:如下图所示:
,
,
由平面镜原理得:,平分,,
,
,
当和互换位置时,.
第1页,共1页
同课章节目录
