10.5.2 角平分线的性质与判定的综合应用(学案含答案)
文档属性
| 名称 | 10.5.2 角平分线的性质与判定的综合应用(学案含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-04 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第十章 三角形的有关证明
5 角平分线
第2课时角平分线的性质与判定的综合应用
知识梳理
三角形的三条角平分线的性质
三角形的三条角平分线相交于一点,并且这一点到三条边的距离__________.
当堂达标
1.如图所示是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC 三条中线的交点 B.△ABC 三条角平分线的交点
C.△ABC 三条高所在直线的交点 D.△ABC 三边的垂直平分线的交点
第1题图 第2题图
2.如图是一个风筝骨架,为使风筝平衡,须使我们已知 OB,那么 PC 和PD 应满足___________,才能保证OP 为 的平分线.
3.如图所示,BD 平分 点 P在BD 上, 点 M,N 为垂足.求证:
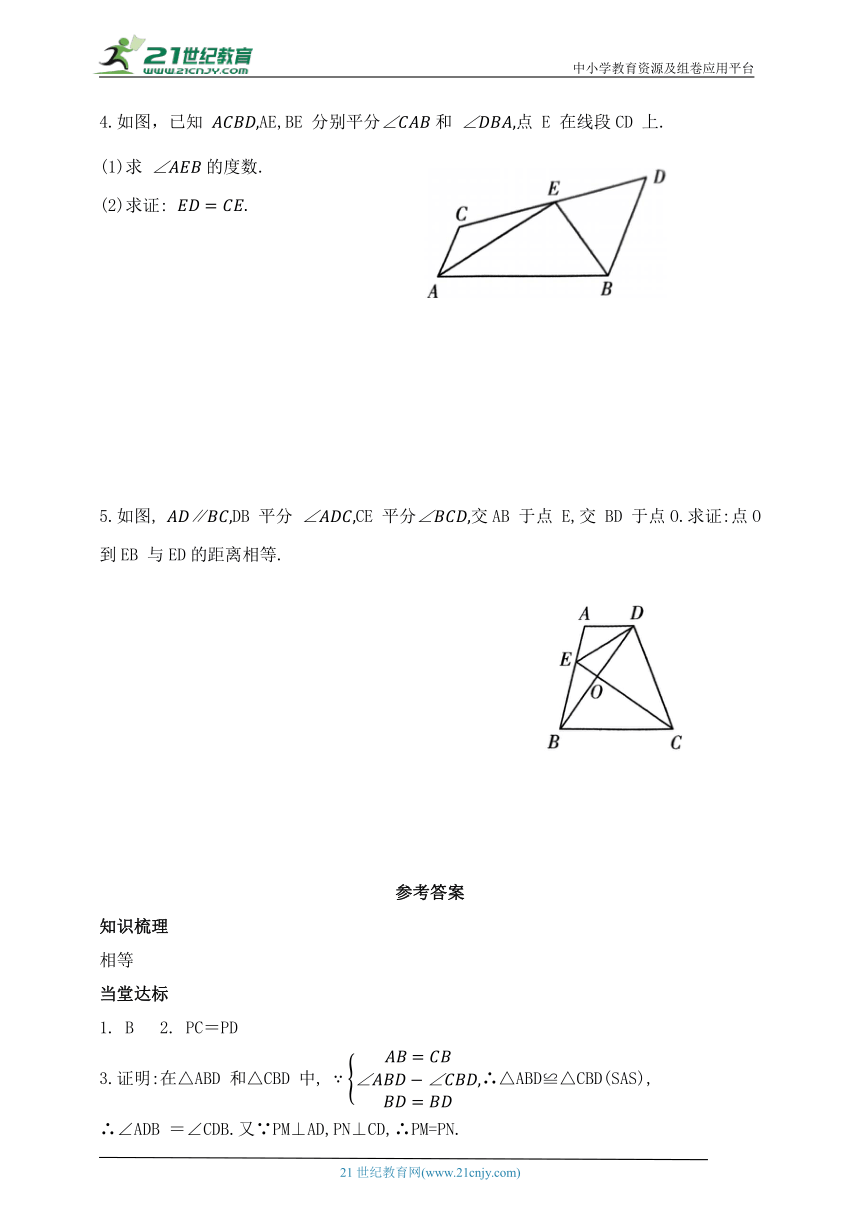
4.如图,已知 AE,BE 分别平分和 点 E 在线段CD 上.
(1)求 的度数.
(2)求证:
5.如图, ∥DB 平分 CE 平分交AB 于点 E,交 BD 于点O.求证:点O到EB 与ED的距离相等.
参考答案
知识梳理
相等
当堂达标
1. B 2. PC=PD
3.证明:在△ABD 和△CBD 中, ∴△ABD≌△CBD(SAS),
∴∠ADB =∠CDB.又∵PM⊥AD,PN⊥CD,∴PM=PN.
4.(1)解:∵AC∥BD,∴∠CAB+∠ABD=180°.
∵AE平分
同理可得∠EBA= ∠ABD,∴∠EAB+∠EBA=90°.∴∠AEB=90°.
(2)证明:如图,在 AB 上截取 AF=AC,连接EF.
在△ACE 和△AFE 中. ,△AFE(SAS),
∴ CE = FE,∠CEA = ∠FEA.
∵∠CEA+∠DEB=90°,∠FEA +∠FEB =90°.∴∠DEB - ∠FEB.
在 △DEB 和 △FEB 中,,∴△DEB≌△FEB(ASA).
∴ED=EF,∴ED=CE.
5.证明:∵AD∥BC,∴∠ADC+∠BCD=180°.
∵DB平分∠ADC. CE平分∠BCD.∴∠ODC|∠OCD=90°.∴∠DOC=90°.
又∵CE 平分∠BCD,∴∠DCO=∠BCO.
又∵OC-OC.∠DOC--∠BOC - 90°.∴△DOC≌△BOC(ASA).∴CD=CB.
∵∠DCE=∠BCE,EC=EC,∴△DCE≌△BCE(SAS),∴∠DEO-∠BEO.
∴EC 平分∠BED.∴点O到EB与ED 的距离相等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十章 三角形的有关证明
5 角平分线
第2课时角平分线的性质与判定的综合应用
知识梳理
三角形的三条角平分线的性质
三角形的三条角平分线相交于一点,并且这一点到三条边的距离__________.
当堂达标
1.如图所示是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC 三条中线的交点 B.△ABC 三条角平分线的交点
C.△ABC 三条高所在直线的交点 D.△ABC 三边的垂直平分线的交点
第1题图 第2题图
2.如图是一个风筝骨架,为使风筝平衡,须使我们已知 OB,那么 PC 和PD 应满足___________,才能保证OP 为 的平分线.
3.如图所示,BD 平分 点 P在BD 上, 点 M,N 为垂足.求证:
4.如图,已知 AE,BE 分别平分和 点 E 在线段CD 上.
(1)求 的度数.
(2)求证:
5.如图, ∥DB 平分 CE 平分交AB 于点 E,交 BD 于点O.求证:点O到EB 与ED的距离相等.
参考答案
知识梳理
相等
当堂达标
1. B 2. PC=PD
3.证明:在△ABD 和△CBD 中, ∴△ABD≌△CBD(SAS),
∴∠ADB =∠CDB.又∵PM⊥AD,PN⊥CD,∴PM=PN.
4.(1)解:∵AC∥BD,∴∠CAB+∠ABD=180°.
∵AE平分
同理可得∠EBA= ∠ABD,∴∠EAB+∠EBA=90°.∴∠AEB=90°.
(2)证明:如图,在 AB 上截取 AF=AC,连接EF.
在△ACE 和△AFE 中. ,△AFE(SAS),
∴ CE = FE,∠CEA = ∠FEA.
∵∠CEA+∠DEB=90°,∠FEA +∠FEB =90°.∴∠DEB - ∠FEB.
在 △DEB 和 △FEB 中,,∴△DEB≌△FEB(ASA).
∴ED=EF,∴ED=CE.
5.证明:∵AD∥BC,∴∠ADC+∠BCD=180°.
∵DB平分∠ADC. CE平分∠BCD.∴∠ODC|∠OCD=90°.∴∠DOC=90°.
又∵CE 平分∠BCD,∴∠DCO=∠BCO.
又∵OC-OC.∠DOC--∠BOC - 90°.∴△DOC≌△BOC(ASA).∴CD=CB.
∵∠DCE=∠BCE,EC=EC,∴△DCE≌△BCE(SAS),∴∠DEO-∠BEO.
∴EC 平分∠BED.∴点O到EB与ED 的距离相等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
