直线与平面平行的判定
图片预览


文档简介
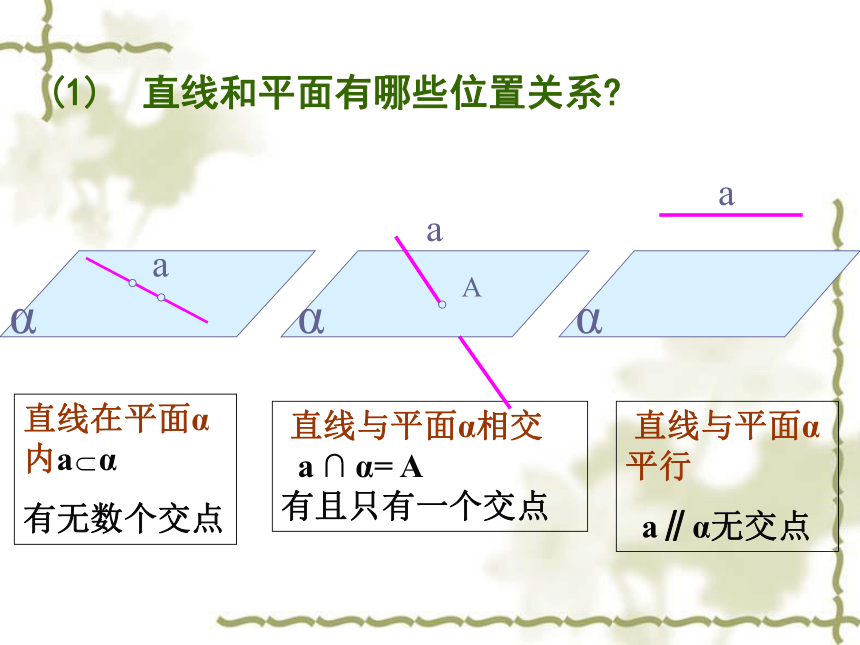
课件9张PPT。 2.2.1 直线与平面平行的判定(1) 直线和平面有哪些位置关系? 直线与平面α相交
a ∩ α= A
有且只有一个交点 直线与平面α平行
a∥α无交点直线在平面α内a α
有无数个交点 定义:一条直线和一个平面没有公共点,
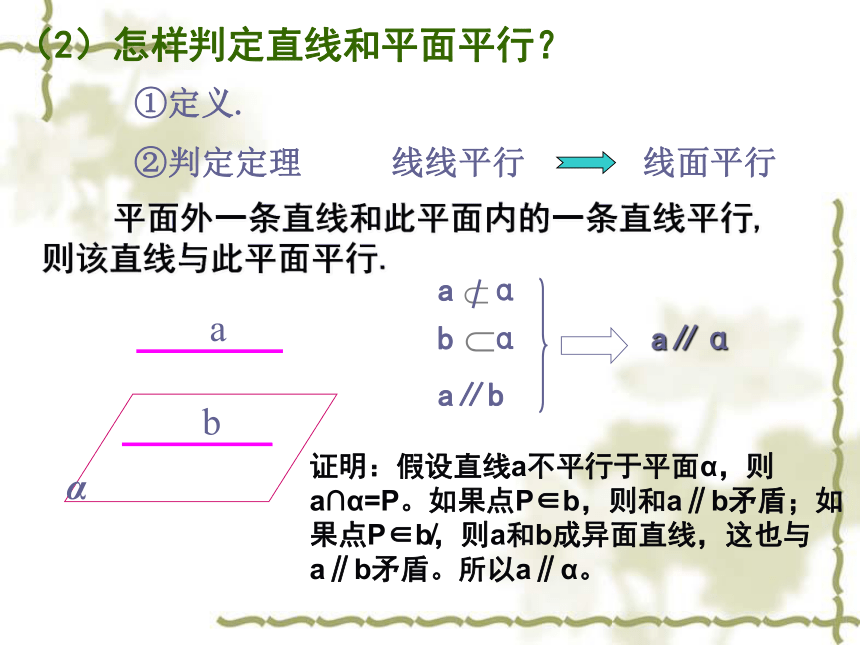
叫做直线与平面平行. (2)怎样判定直线和平面平行? ①定义. ②判定定理 平面外一条直线和此平面内的一条直线平行,则该直线与此平面平行.练习:
(1)直线 a∥平面α,平面α内有 n 条互相平行的直线,
那么这 n 条直线和直线 a ( )
(A)全平行 (B)全异面
(C)全平行或全异面 (D)不全平行也不全异面
(2)直线 a∥平面α,平面α内有无数条直线 交于 一点,那
么这无数条直线中与直线 a 平行的( )
(A)至少有一条 (B)至多有一条
(C)有且只有一条 (D)不可能有
CB例1、求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面。求证:EF∥平面BCD例题分析已知:空间四边形ABCD,E、F分别是AB、AD的中点。
已知P、Q是边长为1的正方体ABCD-A1B1C1D1
的面AA1DD1 、面ABCD的中心(1)求证:PQ// 平面DD1C1C(2)求线段的PQ长PQ练习31、如果两个相交平面分别经过两条平行直线
中的一条,那么它们的交线和这两条直线平行. 课后练习小结 如果不在一个平面内的一条直线和平面内的
一条直线平行,那么这条直线和这个平面平行.
线线平行 线面平行线面平行的判定定理
a ∩ α= A
有且只有一个交点 直线与平面α平行
a∥α无交点直线在平面α内a α
有无数个交点 定义:一条直线和一个平面没有公共点,
叫做直线与平面平行. (2)怎样判定直线和平面平行? ①定义. ②判定定理 平面外一条直线和此平面内的一条直线平行,则该直线与此平面平行.练习:
(1)直线 a∥平面α,平面α内有 n 条互相平行的直线,
那么这 n 条直线和直线 a ( )
(A)全平行 (B)全异面
(C)全平行或全异面 (D)不全平行也不全异面
(2)直线 a∥平面α,平面α内有无数条直线 交于 一点,那
么这无数条直线中与直线 a 平行的( )
(A)至少有一条 (B)至多有一条
(C)有且只有一条 (D)不可能有
CB例1、求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面。求证:EF∥平面BCD例题分析已知:空间四边形ABCD,E、F分别是AB、AD的中点。
已知P、Q是边长为1的正方体ABCD-A1B1C1D1
的面AA1DD1 、面ABCD的中心(1)求证:PQ// 平面DD1C1C(2)求线段的PQ长PQ练习31、如果两个相交平面分别经过两条平行直线
中的一条,那么它们的交线和这两条直线平行. 课后练习小结 如果不在一个平面内的一条直线和平面内的
一条直线平行,那么这条直线和这个平面平行.
线线平行 线面平行线面平行的判定定理
