人教版数学八年级下册期末测试卷(含答案)
文档属性
| 名称 | 人教版数学八年级下册期末测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 955.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-04 11:49:08 | ||
图片预览



文档简介
期末测试卷
一、选择题(本大题有6个小题,每小题3分,共18分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.判断下列四组数据,可以作为直角三角形三条边长的是( )
A.,, B.,, C.,,() D.1,2,3.
2.下列计算错误的是( )
A. B.
C. D.
3.对于函数,下列说法正确的是( )
A.图象经过点 B.y随着x的增大而减小
C.图象与y轴的交点是(6,0) D.图象与坐标轴围成的三角形面积是9
4.劳动教育是学校贯彻“五育并举”的重要举措,某校倡议学生在家做一些力所能及的家务劳动.李老师为了解学生每周参加家务劳动的时间,随机调查了本班名学生,收集到如下数据:
时间/h 6 5 4 3 2
人数/名 2 6 4 6 2
关于家务劳动时间的描述正确的是( )
A.众数是6 B.平均数是4 C.中位数是3 D.方差是1
5.如图,把一张矩形纸片按如下方法进行两次折叠:第一次将边折叠到边上得到,折痕为,连接,,第二次将沿着折叠,恰好落在边上.则该矩形纸片的长宽比的值为( )
A. B. C. D.
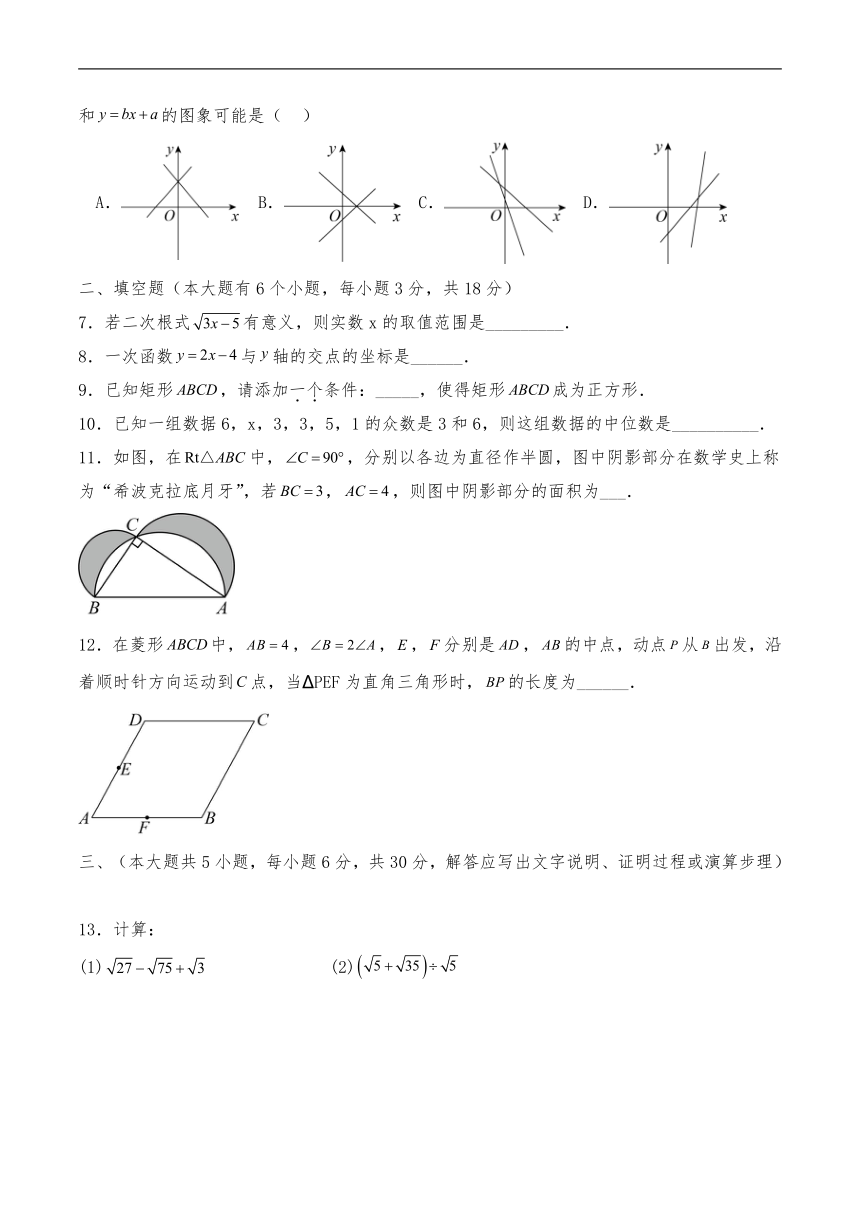
6.已知一次函数的图象经过点,其中,,则关于的一次函数和的图象可能是( )
A. B. C. D.
二、填空题(本大题有6个小题,每小题3分,共18分)
7.若二次根式有意义,则实数x的取值范围是_________.
8.一次函数与轴的交点的坐标是______.
9.已知矩形,请添加一个条件:_____,使得矩形成为正方形.
10.已知一组数据6,x,3,3,5,1的众数是3和6,则这组数据的中位数是__________.
11.如图,在中,,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,若,,则图中阴影部分的面积为___.
12.在菱形中,,,,分别是,的中点,动点从出发,沿着顺时针方向运动到点,当 PEF为直角三角形时,的长度为______.
三、(本大题共5小题,每小题6分,共30分,解答应写出文字说明、证明过程或演算步理)
13.计算:
(1) (2)
14.已知y与成正比例,当时,.
(1)求y与x的函数解析式;
(2)若(1)中函数的图象与一次函数的图象相交于点A,求点A的坐标.
15.如图,在四边形中,,,垂足分别为点E,F,连接.
(1)请你只添加一个条件(不另加辅助线),使得四边形为平行四边形,你添加的条件是 ;
(2)在(1)中添加条件后,请证明四边形为平行四边形.
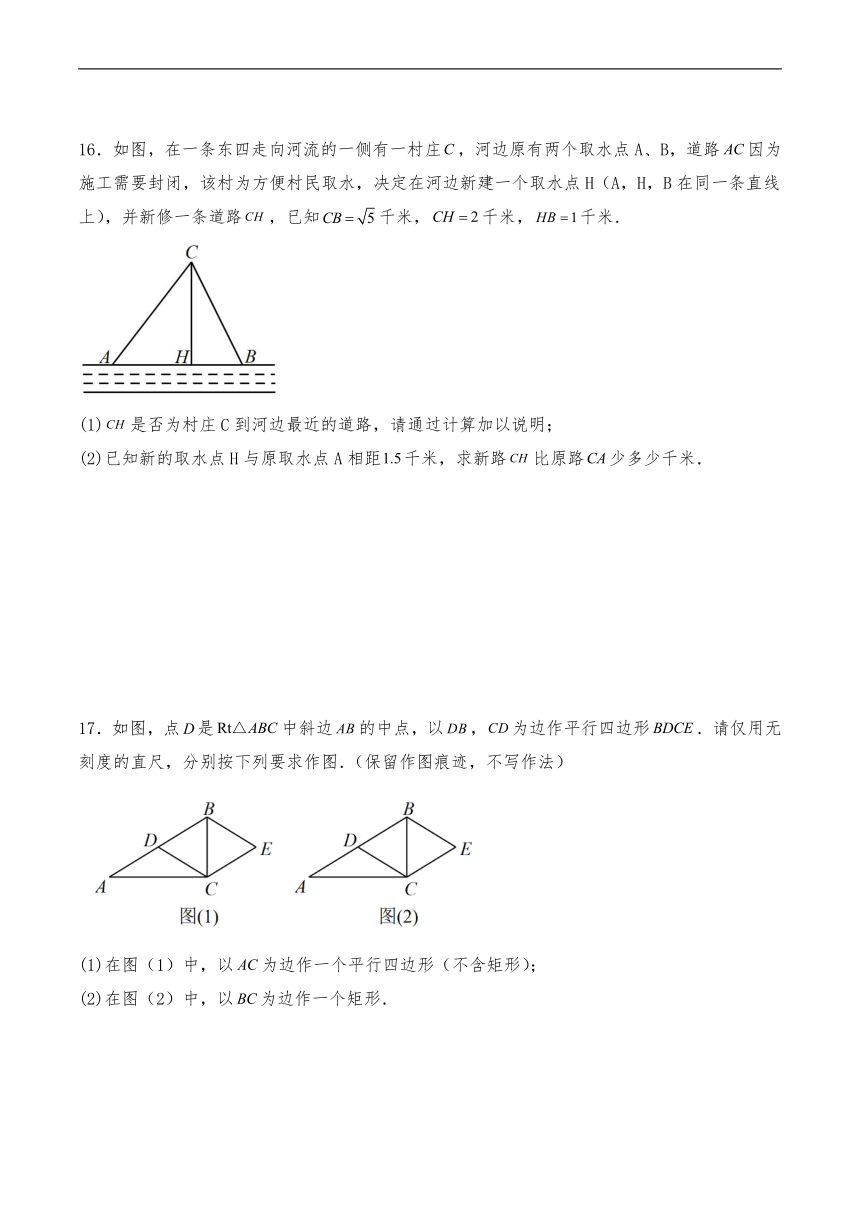
16.如图,在一条东四走向河流的一侧有一村庄,河边原有两个取水点A、B,道路因为施工需要封闭,该村为方便村民取水,决定在河边新建一个取水点H(A,H,B在同一条直线上),并新修一条道路,已知千米,千米,千米.
(1)是否为村庄C到河边最近的道路,请通过计算加以说明;
(2)已知新的取水点H与原取水点A相距千米,求新路比原路少多少千米.
17.如图,点是中斜边的中点,以,为边作平行四边形.请仅用无刻度的直尺,分别按下列要求作图.(保留作图痕迹,不写作法)
(1)在图(1)中,以为边作一个平行四边形(不含矩形);
(2)在图(2)中,以为边作一个矩形.
四、(本大题共3小题,每小题8分,共24分,解答应写出文字说明、证明过程或演算步理)
18.沙坪坝区积极创建新时代“红岩大课堂”,是学习贯彻党的二十大精神的重要实践.某校组织全校学生参加了“冠红岩之名 铸红岩之魂”的知识竞赛.现从该校八、九年级中各随机抽取10名学生的竞赛成绩(单位:分,满分100分),并进行整理、描述和分析(竞赛成绩用表示,共分成,,,四个等级:;;;),下面给出了部分信息:
八年级10名学生的竞赛成绩:94,93,85,83,79,78,78,78,67,61.
九年级10名学生中等级所有学生的竞赛成绩:83,83,83,81.
八、九年级抽取的学生竞赛成绩统计表
年级 平均数 中位数 众数 方差
八年级 79.6 78.5 104.5
九年级 79.6 83 82.7
根据以上信息,解答下列问题:
(1)填空:__________,__________,__________;
(2)若竞赛成绩超过90分的学生获“红岩少年”称号,请估计该校八年级460名学生中,获“红岩少年”称号的人数;
(3)根据以上数据,你认为在此次竞赛中,哪个年级的成绩更好?请说明理由(写出一条理由即可).
19.定义:如图,点M、N把线段分割成,若以为边的三角形是一个直角三角形,则称点M、N是线段的勾股分割点.
(1)已知M、N把线段分割成,若,,,则点M、N是线段的勾股分割点吗?请说明理由.
(2)已知点M、N是线段AB的勾股分割点,且AM为直角边,若,,求BN的长.
20.某电商根据市场需求购进一批A,B两种型号的电脑小音箱进行销售,每台B型音箱的进价比A型音箱的进价多10元,用6000元购进A型音箱与用8000元购进B型音箱的台数相同.
(1)求A,B两种型号的电脑小音箱的单价;
(2)该电商计划购进A,B两种型号的电脑小音箱共100台进行销售,其中A型音箱台数不小于B型音箱台数的3倍,A型音箱每台售价35元,B型音箱每台售价48元,怎样安排进货才能使售完这100台电脑小音箱所获利润最大?最大利润是多少元?
(3)为满足不同顾客的需要,该电商准备新增购进进价为每台20元的C型音箱,A,B两种型号音箱仍按需购进,进价不变,A型音箱的台数是B型音箱台数的5倍,共花费20000元,则该电商至少可以购进三种型号音箱共多少台?
五、(本大题共2小题,每小题9分,共18分,解答应写出文字说明、证明过程或演算步理)
21.先阅读,后解答:
,;
像上述解题过程中,与、与相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化.
(1)的有理化因式是______;的有理化因式是______.
(2)将下列式子进行分母有理化:
①______;②______;③______;④______.
(3)类比(2)中④的计算结果,计算:.
22.如图1,在平面直角坐标系中,直线:与x轴交于点,与y轴交于点B.
(1)求直线的解析式;
(2)若直线 :与x轴、y轴、直线分别交于点C、D、E,求面积;
(3)如图2,在(2)的条件下,点F为线段上一动点,将沿直线翻折得到,交x轴于点M.当为直角三角形时,求点N的坐标.
六、(本大题共12分,解答应写出文字说明、证明过程或演算步理)
23.小新学习了特殊的四边形一平行四边形后,对特殊四边形的探究产生了兴趣,发现另外一类特殊四边形,如图1,我们把两条对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是______.
(2)性质探究:通过探究,直接写出垂美四边形的面积S与两对角线,之间的数量关系:______.
(3)问题解决:如图2,分别以的直角边和斜边为边向外作正方形和正方形,连接已知,.
①求证:四边形为垂美四边形;
②直接写出四边形的面积.
参考答案
一、选择题
1 2 3 4 5 6
A C B B D B
二、填空题
7. 8. 9.(答案不唯一)
10.4 11.6 12.3或或
三、
13.(1)解:原式
;
(2)原式
.
14.(1)解:设函数解析式为:,
∵当时,,
∴,解得:,
∴y与x的函数解析式为:;
(2)解:根据题意,建立方程组,解得,
∴点A的坐标为:.
15.(1)解:;
根据,,可得,
再添加,利用一组对边平行且相等的四边形是平行四边形可判定;
故答案为:(答案不唯一).
(2)证明:∵,,
∴,
∵,
∴四边形是平行四边形.
16.(1)解:是,说明如下:
∵在中,,
又,
是以为直角的直角三角形,
,
∵点到直线垂线段的长度最短,
是村庄C到河边的最近路.
(2)由题意,得:(千米)
在中,由勾股定理得:(千米),
比少千米.
17.(1)解:如图(1)连接,四边形是平行四边形,即为所求.
(2)解:如图(2),连接交于,连接交于,连接并延长交于,交于,连接、并延长,交点为,连接,则四边形是矩形,矩形即为所求.
四、
18.(1)由题意可知,八年级10名学生成绩出现次数最多的是78,共出现3次,因此众数是78,即,
九年级成绩在“B组”的有4人,占,
,
九年级10名同学成绩从小到大排列后,处在中间位置的两个数都是在“B组”,分别为81,83,
因此中位数是,即;
故答案为:78,82,30;
(2).
答:估计该校八年级学生获“红岩少年”称号的人数为92人.
(3)九年级学生竞赛成绩更好.理由如下(写出其中一条即可):
①九年级学生竞赛成绩中位数82高于八年级学生竞赛成绩中位数78.5.
②九年级学生竞赛成绩方差82.7低于八年级学生竞赛成绩方差104.5.
③九年级学生竞赛成绩众数83高于八年级学生竞赛成绩众数78.
19.(1)点M、N是线段的勾股分割点,理由如下:
∵,,
∴,
∴
∴以为边的三角形是直角三角形
∴点M、N是线段的勾股分割点;
(2)设
∵,
∴
∵点M、N是线段的勾股分割点,且为直角边
∴①若为斜边,则
即,
解得:
②若为斜边,则
即,
解得:
综上所述,BN的长为或.
20.(1)解:设每台A型音箱的进价为x元,每台B型音箱的进价为元,
由题意得:,
解得,
经检验,是原分式方程的解,且符合题意,
∴,
答:每台A型音箱的进价为30元,则每台B型音箱的进价为40元;
(2)解:设最大利润是元,购进a台A型音箱,则购进台B型音箱,
由题意得:,
∵A型音箱台数不小于B型音箱台数的3倍,
∴,解得,
∵,
∴随x的增大而减小,
∴当时,取最大值,最大值为575;
答:购进75台A型音箱,购进25台B型音箱所获利润最大,最大利润是575元;
(3)解:设购进b台B型音箱,则购进台A型音箱,购进三种音箱共n台,则购进的C型音箱台,
由题意得:,
解得,
∵,
∴,解得,
∵b为正整数且为2的倍数,
∴,
∵,
∴n随b的增大而减小,
当时,最小,,
答:该电商至少可以购进三种型号音箱共636台.
五、
21.(1)解: 的有理化因式是,的有理化因式是.
故答案为:,.
(2)解∶①;
②;
③;
②.
故答案为:、、、.
(3)解:
.
22.(1)解:把代入得,
∴,
∴直线:;
(2)∵直线:,
∴点B的坐标为,
∵直线 :与x轴、y轴、直线分别交于点C、D、E,
当时,,当时,,解得,
∴、,
联立与得,解得,
∴,
∴,
∴,
∴的面积为;
(3)如图2,当时,过点E作轴于H,
由翻折得,
∴,
∵,
∴,,
∴,
∴ ,
∵,
∴,
由翻折得,
∴点N的坐标为;
如图3,当时,
由翻折得,
∵,,
∴,,
∴,
∴点N的坐标为;
综上,点N的坐标为或.
六、
23.(1)∵在平行四边形、矩形、菱形、正方形中,两条对角线互相垂直的四边形是菱形、正方形,
∴菱形和正方形一定是垂美四边形;
故答案为:菱形、正方形;
(2)如图1所示:
∵四边形的面积=的面积+的面积
=;
故答案为:;
(3)①证明:连接交于N,交于M,如图2所示:
∵四边形和四边形是正方形,
∴,,,
∴,
即,
在和中,
,
∴,
∴,,
又∵,,
∴,
∴,
∴四边形为垂美四边形;
②∵
∴
∴,
在中,
∴,
∵四边形为垂美四边形,
∴四边形的面积
一、选择题(本大题有6个小题,每小题3分,共18分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.判断下列四组数据,可以作为直角三角形三条边长的是( )
A.,, B.,, C.,,() D.1,2,3.
2.下列计算错误的是( )
A. B.
C. D.
3.对于函数,下列说法正确的是( )
A.图象经过点 B.y随着x的增大而减小
C.图象与y轴的交点是(6,0) D.图象与坐标轴围成的三角形面积是9
4.劳动教育是学校贯彻“五育并举”的重要举措,某校倡议学生在家做一些力所能及的家务劳动.李老师为了解学生每周参加家务劳动的时间,随机调查了本班名学生,收集到如下数据:
时间/h 6 5 4 3 2
人数/名 2 6 4 6 2
关于家务劳动时间的描述正确的是( )
A.众数是6 B.平均数是4 C.中位数是3 D.方差是1
5.如图,把一张矩形纸片按如下方法进行两次折叠:第一次将边折叠到边上得到,折痕为,连接,,第二次将沿着折叠,恰好落在边上.则该矩形纸片的长宽比的值为( )
A. B. C. D.
6.已知一次函数的图象经过点,其中,,则关于的一次函数和的图象可能是( )
A. B. C. D.
二、填空题(本大题有6个小题,每小题3分,共18分)
7.若二次根式有意义,则实数x的取值范围是_________.
8.一次函数与轴的交点的坐标是______.
9.已知矩形,请添加一个条件:_____,使得矩形成为正方形.
10.已知一组数据6,x,3,3,5,1的众数是3和6,则这组数据的中位数是__________.
11.如图,在中,,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,若,,则图中阴影部分的面积为___.
12.在菱形中,,,,分别是,的中点,动点从出发,沿着顺时针方向运动到点,当 PEF为直角三角形时,的长度为______.
三、(本大题共5小题,每小题6分,共30分,解答应写出文字说明、证明过程或演算步理)
13.计算:
(1) (2)
14.已知y与成正比例,当时,.
(1)求y与x的函数解析式;
(2)若(1)中函数的图象与一次函数的图象相交于点A,求点A的坐标.
15.如图,在四边形中,,,垂足分别为点E,F,连接.
(1)请你只添加一个条件(不另加辅助线),使得四边形为平行四边形,你添加的条件是 ;
(2)在(1)中添加条件后,请证明四边形为平行四边形.
16.如图,在一条东四走向河流的一侧有一村庄,河边原有两个取水点A、B,道路因为施工需要封闭,该村为方便村民取水,决定在河边新建一个取水点H(A,H,B在同一条直线上),并新修一条道路,已知千米,千米,千米.
(1)是否为村庄C到河边最近的道路,请通过计算加以说明;
(2)已知新的取水点H与原取水点A相距千米,求新路比原路少多少千米.
17.如图,点是中斜边的中点,以,为边作平行四边形.请仅用无刻度的直尺,分别按下列要求作图.(保留作图痕迹,不写作法)
(1)在图(1)中,以为边作一个平行四边形(不含矩形);
(2)在图(2)中,以为边作一个矩形.
四、(本大题共3小题,每小题8分,共24分,解答应写出文字说明、证明过程或演算步理)
18.沙坪坝区积极创建新时代“红岩大课堂”,是学习贯彻党的二十大精神的重要实践.某校组织全校学生参加了“冠红岩之名 铸红岩之魂”的知识竞赛.现从该校八、九年级中各随机抽取10名学生的竞赛成绩(单位:分,满分100分),并进行整理、描述和分析(竞赛成绩用表示,共分成,,,四个等级:;;;),下面给出了部分信息:
八年级10名学生的竞赛成绩:94,93,85,83,79,78,78,78,67,61.
九年级10名学生中等级所有学生的竞赛成绩:83,83,83,81.
八、九年级抽取的学生竞赛成绩统计表
年级 平均数 中位数 众数 方差
八年级 79.6 78.5 104.5
九年级 79.6 83 82.7
根据以上信息,解答下列问题:
(1)填空:__________,__________,__________;
(2)若竞赛成绩超过90分的学生获“红岩少年”称号,请估计该校八年级460名学生中,获“红岩少年”称号的人数;
(3)根据以上数据,你认为在此次竞赛中,哪个年级的成绩更好?请说明理由(写出一条理由即可).
19.定义:如图,点M、N把线段分割成,若以为边的三角形是一个直角三角形,则称点M、N是线段的勾股分割点.
(1)已知M、N把线段分割成,若,,,则点M、N是线段的勾股分割点吗?请说明理由.
(2)已知点M、N是线段AB的勾股分割点,且AM为直角边,若,,求BN的长.
20.某电商根据市场需求购进一批A,B两种型号的电脑小音箱进行销售,每台B型音箱的进价比A型音箱的进价多10元,用6000元购进A型音箱与用8000元购进B型音箱的台数相同.
(1)求A,B两种型号的电脑小音箱的单价;
(2)该电商计划购进A,B两种型号的电脑小音箱共100台进行销售,其中A型音箱台数不小于B型音箱台数的3倍,A型音箱每台售价35元,B型音箱每台售价48元,怎样安排进货才能使售完这100台电脑小音箱所获利润最大?最大利润是多少元?
(3)为满足不同顾客的需要,该电商准备新增购进进价为每台20元的C型音箱,A,B两种型号音箱仍按需购进,进价不变,A型音箱的台数是B型音箱台数的5倍,共花费20000元,则该电商至少可以购进三种型号音箱共多少台?
五、(本大题共2小题,每小题9分,共18分,解答应写出文字说明、证明过程或演算步理)
21.先阅读,后解答:
,;
像上述解题过程中,与、与相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化.
(1)的有理化因式是______;的有理化因式是______.
(2)将下列式子进行分母有理化:
①______;②______;③______;④______.
(3)类比(2)中④的计算结果,计算:.
22.如图1,在平面直角坐标系中,直线:与x轴交于点,与y轴交于点B.
(1)求直线的解析式;
(2)若直线 :与x轴、y轴、直线分别交于点C、D、E,求面积;
(3)如图2,在(2)的条件下,点F为线段上一动点,将沿直线翻折得到,交x轴于点M.当为直角三角形时,求点N的坐标.
六、(本大题共12分,解答应写出文字说明、证明过程或演算步理)
23.小新学习了特殊的四边形一平行四边形后,对特殊四边形的探究产生了兴趣,发现另外一类特殊四边形,如图1,我们把两条对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是______.
(2)性质探究:通过探究,直接写出垂美四边形的面积S与两对角线,之间的数量关系:______.
(3)问题解决:如图2,分别以的直角边和斜边为边向外作正方形和正方形,连接已知,.
①求证:四边形为垂美四边形;
②直接写出四边形的面积.
参考答案
一、选择题
1 2 3 4 5 6
A C B B D B
二、填空题
7. 8. 9.(答案不唯一)
10.4 11.6 12.3或或
三、
13.(1)解:原式
;
(2)原式
.
14.(1)解:设函数解析式为:,
∵当时,,
∴,解得:,
∴y与x的函数解析式为:;
(2)解:根据题意,建立方程组,解得,
∴点A的坐标为:.
15.(1)解:;
根据,,可得,
再添加,利用一组对边平行且相等的四边形是平行四边形可判定;
故答案为:(答案不唯一).
(2)证明:∵,,
∴,
∵,
∴四边形是平行四边形.
16.(1)解:是,说明如下:
∵在中,,
又,
是以为直角的直角三角形,
,
∵点到直线垂线段的长度最短,
是村庄C到河边的最近路.
(2)由题意,得:(千米)
在中,由勾股定理得:(千米),
比少千米.
17.(1)解:如图(1)连接,四边形是平行四边形,即为所求.
(2)解:如图(2),连接交于,连接交于,连接并延长交于,交于,连接、并延长,交点为,连接,则四边形是矩形,矩形即为所求.
四、
18.(1)由题意可知,八年级10名学生成绩出现次数最多的是78,共出现3次,因此众数是78,即,
九年级成绩在“B组”的有4人,占,
,
九年级10名同学成绩从小到大排列后,处在中间位置的两个数都是在“B组”,分别为81,83,
因此中位数是,即;
故答案为:78,82,30;
(2).
答:估计该校八年级学生获“红岩少年”称号的人数为92人.
(3)九年级学生竞赛成绩更好.理由如下(写出其中一条即可):
①九年级学生竞赛成绩中位数82高于八年级学生竞赛成绩中位数78.5.
②九年级学生竞赛成绩方差82.7低于八年级学生竞赛成绩方差104.5.
③九年级学生竞赛成绩众数83高于八年级学生竞赛成绩众数78.
19.(1)点M、N是线段的勾股分割点,理由如下:
∵,,
∴,
∴
∴以为边的三角形是直角三角形
∴点M、N是线段的勾股分割点;
(2)设
∵,
∴
∵点M、N是线段的勾股分割点,且为直角边
∴①若为斜边,则
即,
解得:
②若为斜边,则
即,
解得:
综上所述,BN的长为或.
20.(1)解:设每台A型音箱的进价为x元,每台B型音箱的进价为元,
由题意得:,
解得,
经检验,是原分式方程的解,且符合题意,
∴,
答:每台A型音箱的进价为30元,则每台B型音箱的进价为40元;
(2)解:设最大利润是元,购进a台A型音箱,则购进台B型音箱,
由题意得:,
∵A型音箱台数不小于B型音箱台数的3倍,
∴,解得,
∵,
∴随x的增大而减小,
∴当时,取最大值,最大值为575;
答:购进75台A型音箱,购进25台B型音箱所获利润最大,最大利润是575元;
(3)解:设购进b台B型音箱,则购进台A型音箱,购进三种音箱共n台,则购进的C型音箱台,
由题意得:,
解得,
∵,
∴,解得,
∵b为正整数且为2的倍数,
∴,
∵,
∴n随b的增大而减小,
当时,最小,,
答:该电商至少可以购进三种型号音箱共636台.
五、
21.(1)解: 的有理化因式是,的有理化因式是.
故答案为:,.
(2)解∶①;
②;
③;
②.
故答案为:、、、.
(3)解:
.
22.(1)解:把代入得,
∴,
∴直线:;
(2)∵直线:,
∴点B的坐标为,
∵直线 :与x轴、y轴、直线分别交于点C、D、E,
当时,,当时,,解得,
∴、,
联立与得,解得,
∴,
∴,
∴,
∴的面积为;
(3)如图2,当时,过点E作轴于H,
由翻折得,
∴,
∵,
∴,,
∴,
∴ ,
∵,
∴,
由翻折得,
∴点N的坐标为;
如图3,当时,
由翻折得,
∵,,
∴,,
∴,
∴点N的坐标为;
综上,点N的坐标为或.
六、
23.(1)∵在平行四边形、矩形、菱形、正方形中,两条对角线互相垂直的四边形是菱形、正方形,
∴菱形和正方形一定是垂美四边形;
故答案为:菱形、正方形;
(2)如图1所示:
∵四边形的面积=的面积+的面积
=;
故答案为:;
(3)①证明:连接交于N,交于M,如图2所示:
∵四边形和四边形是正方形,
∴,,,
∴,
即,
在和中,
,
∴,
∴,,
又∵,,
∴,
∴,
∴四边形为垂美四边形;
②∵
∴
∴,
在中,
∴,
∵四边形为垂美四边形,
∴四边形的面积
同课章节目录
