人教版八年级数学下册 期末质量检测卷(含详解)
文档属性
| 名称 | 人教版八年级数学下册 期末质量检测卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 492.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-04 19:02:26 | ||
图片预览



文档简介
期末质量检测卷
一、选择题(共8题,每小题3分,共24分)
1.函数的自变量x的取值范围是( )
A.x≠2 B.x≥2 C.x<0 D.x>2
2.下列各式计算错误的是( )
A. B.
C. D.
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,添加下列条件,能使菱形ABCD成为正方形的是( )
A.AC=BD B.AC⊥BD C.AD=AB D.AC平分∠DAB
4.如图,直线y=kx+b交坐标轴于A(﹣2,0),B(0,1)两点,则不等式﹣kx﹣b<0的解集为( )
A.x>﹣2 B.x<﹣2 C.x>2 D.x<2
5.为了了解某小区居民的用水情况,随机抽查了若干户家庭的某月用水量,统计结果如表所示:
月用水量/吨 3 4 5 6
户数 4 6 8 2
关于这若干户家庭的该月用水量的数据统计分析,下列说法正确的是( )
A.中位数是5 B.平均数是7 C.众数是5 D.方差是1
6.如图,AC是 ABCD的对角线,点E在AC上,AD=AE=BE,∠D=105°,则∠BAC是( )
A.25° B.30° C.45° D.50°
7.若2、5、n为三角形的三边长,则化简的结果为( )
A.5 B.2n﹣11 C.11﹣2n D.﹣5
8.如图,在Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB,AB,CB=4,则△ABD的面积为( )
A.6 B.7 C.10 D.9
9.甲、乙两个工程队分别同时维修两段道路,所维修的道路长度与维修的天数之间的函数关系图象如图所示,下列结论正确的是( )
A.开工第2天时,甲队比乙队多维修200m
B.开工第6天时,甲队比乙队多维修200m
C.甲队维修道路长度为550m时,乙队所维修的道路长度为650m
D.开工第2天或第天时,甲、乙两队所维修道路长度的差为100m
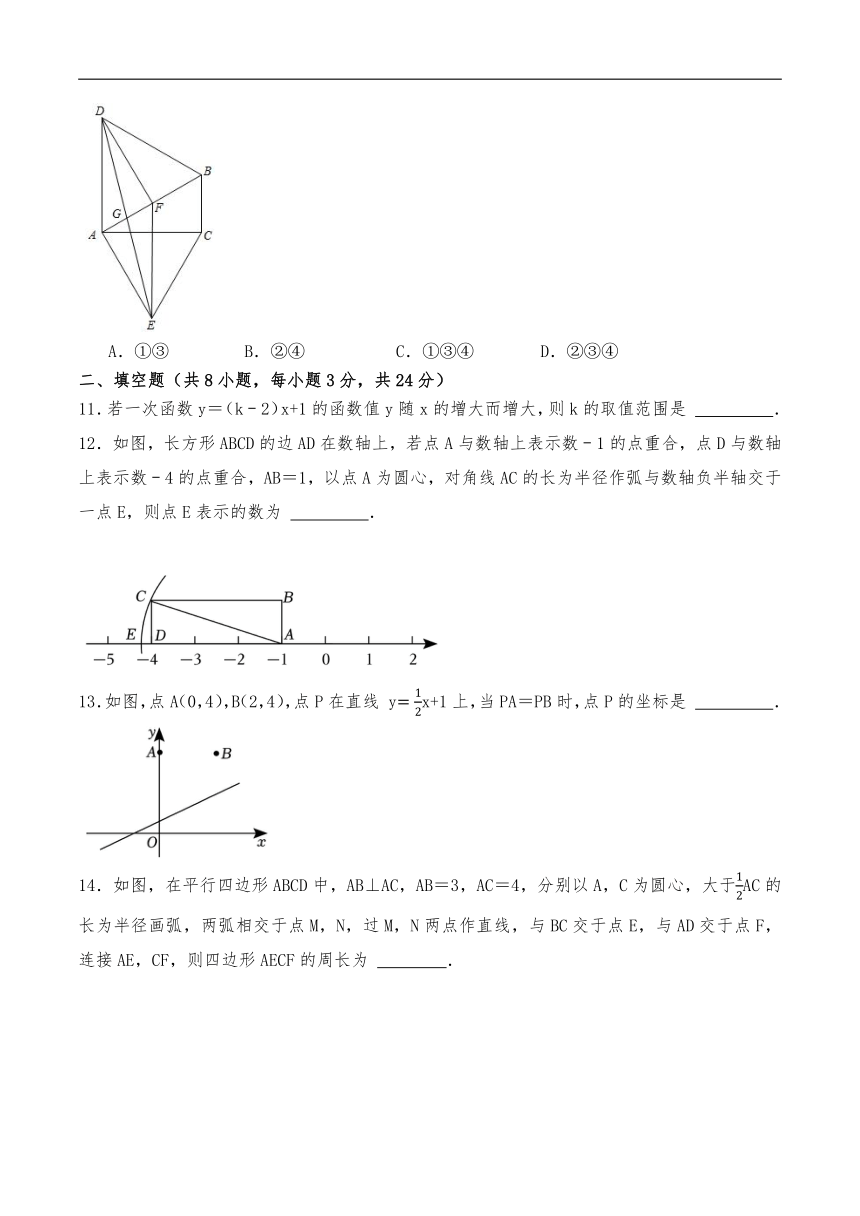
10.如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.则正确结论的序号是( )
A.①③ B.②④ C.①③④ D.②③④
二、填空题(共8小题,每小题3分,共24分)
11.若一次函数y=(k﹣2)x+1的函数值y随x的增大而增大,则k的取值范围是 .
12.如图,长方形ABCD的边AD在数轴上,若点A与数轴上表示数﹣1的点重合,点D与数轴上表示数﹣4的点重合,AB=1,以点A为圆心,对角线AC的长为半径作弧与数轴负半轴交于一点E,则点E表示的数为 .
13.如图,点A(0,4),B(2,4),点P在直线 yx+1上,当PA=PB时,点P的坐标是 .
14.如图,在平行四边形ABCD中,AB⊥AC,AB=3,AC=4,分别以A,C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,过M,N两点作直线,与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为 .
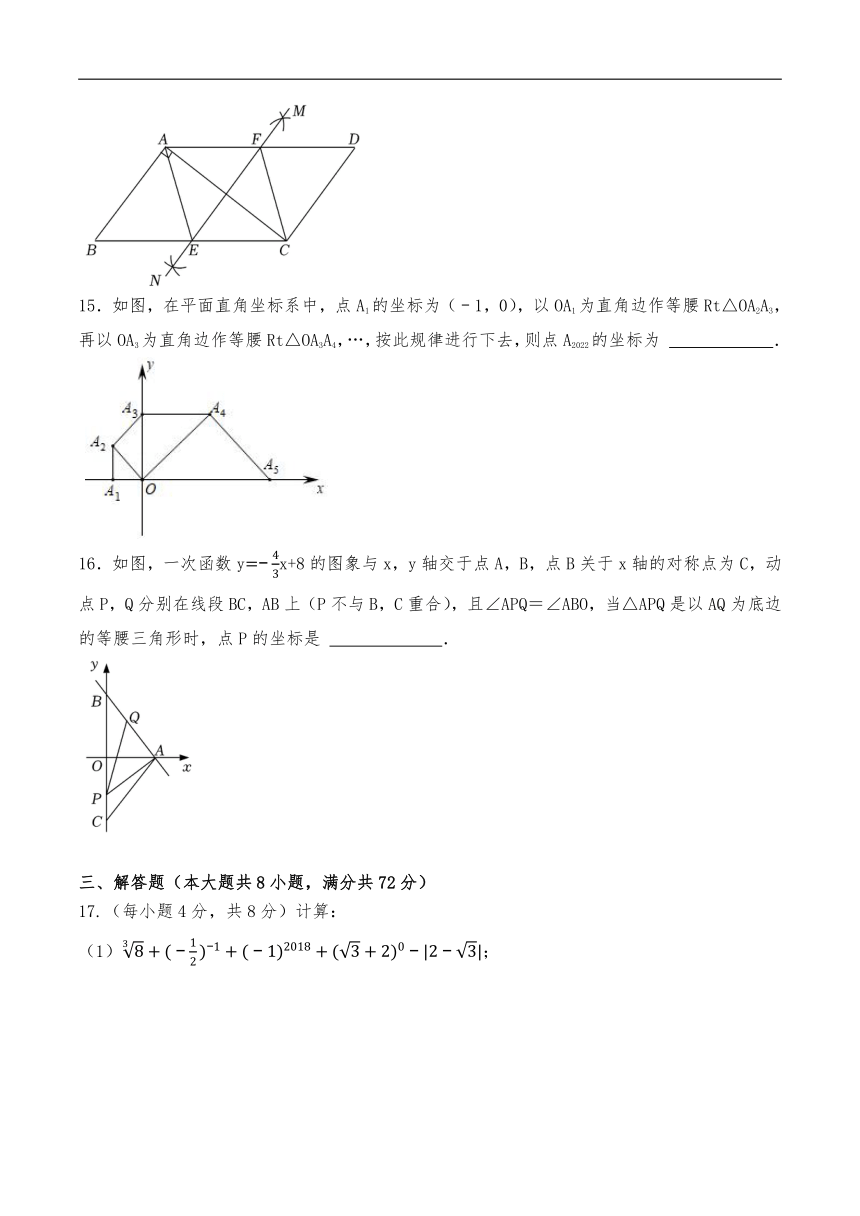
15.如图,在平面直角坐标系中,点A1的坐标为(﹣1,0),以OA1为直角边作等腰Rt△OA2A3,再以OA3为直角边作等腰Rt△OA3A4,…,按此规律进行下去,则点A2022的坐标为 .
16.如图,一次函数yx+8的图象与x,y轴交于点A,B,点B关于x轴的对称点为C,动点P,Q分别在线段BC,AB上(P不与B,C重合),且∠APQ=∠ABO,当△APQ是以AQ为底边的等腰三角形时,点P的坐标是 .
三、解答题(本大题共8小题,满分共72分)
17.(每小题4分,共8分)计算:
(1);
(2).
18.已知:如图,在四边形ABCD中,DE⊥AC,BF⊥AC,垂足分别为E,F,延长DE、BF,分别交AB于点H,交BC于点G,若AD∥BC,AE=CF.
(1)求证:四边形ABCD为平行四边形;
(2)若∠DAH=∠GBA,GF=2,CF=4,求AD的长.
19.(每小题4分,共8分)(1)先化简,再求值:,其中.
(2)已知,,试求代数式2x2﹣5xy+2y2的值.
20.(8分)收集数据:4月23日是世界读书日,某校为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:min)
30 60 81 50 40 110 130 146 90 100
60 81 120 140 70 81 10 20 100 81
整理数据:
课外阅读时间x 0≤x<40 40≤x<80 80≤x<120 120≤x<160
人数 3 a 8 b
分析数据:
平均数 中位数 众数
80 m 81
解决问题:
(1)直接写出a,b,m的值;
(2)样本中的中位数和众数落在哪个范围内?
(3)该校现有学生1600人,估计课外阅读时间在“80≤x<120”内的学生有多少名?
21.(8分)如图,四边形ABCD为某工厂的平面图,经测量AB=BC=AD=80m,CD=80m,且∠ABC=90°.
(1)求∠DAB的度数;
(2)若直线AB为工厂的车辆进出口道路(道路的宽度忽略不计),工作人员想要在点D处安装一个摄像头观察车辆进出工厂的情况,已知摄像头能监控的最远距离为80m,求被监控到的道路长度为多少m?
22.(10分)为了提高同学们学习数学的兴趣,某中学开展主题为“感受数学
魅力,享受数学乐趣”的数学活动.并计划购买A、B两种奖品奖励在数学活动中表现突出的学生,已知购买1件A种奖品和2件B种奖品共需64元,购买2件A种奖品和1件B种奖品共需56元.
(1)每件A、B奖品的价格各是多少元?
(2)根据需要,该学校准备购买A、B两种奖品共80件,设购买a件A种奖品,所需总费用为w元,求w与a的函数关系式,并直接写出a的取值范围;
(3)在(2)的条件下,若要求购买的A种奖品的数量不超过B种奖品数量的3倍,求所需总费用的最小值.
23.(10分)在菱形ABCD中,∠ABC=120°,点M在DA的延长线上,点E是直线BD上的动点,连接ME,将线段ME绕点M逆时针旋转60°得到线段MF,连接EF,DF.
(1)如图①,当点E与点B重合时,请直接写出线段AM与DF的数量关系;
(2)如图②,当点E在BD上时,请写出线段BE,AM,DF之间的数量关系,并给出证明;
(3)当点E在直线BD上时,若AB=6,AD=3AM,BD=2BE,请直接写出线段DF的长.
24.(12分)如图,矩形OABC的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标为(2,3),一次函数yx+b的图象与边OC、AB分别交于点D、E,且OD=BE.点M是直线DE上的一个动点.
(1)求b的值;
(2)连结OM,若三角形ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;
(3)设点N是平面内的一点,以O、D、M、N为顶点的四边形是菱形,直接写出N的坐标.
答案
一、选择题
1.根据二次根式有意义的条件成立不等式,解不等式得到答案.
【解答】解:由题意得:x﹣2≥0,
解得:x≥2,
故选:B.
2.
【分析】根据合并同类二次根式的法则、二次根式的乘法、平方差公式及二次根式的除法分别计算可得.
【解答】解:A、43,此选项计算正确;
B、,此选项计算正确;
C、()2﹣()2=3﹣2=1,此选项计算错误;
D、3,此选项计算正确;
故选:C.
3.
【分析】根据菱形的性质及正方形的判定来添加合适的条件.
【解答】解:要使菱形成为正方形,只要菱形满足以下条件之一即可:
(1)有一个内角是直角,(2)对角线相等,
即∠ABC=90°或AC=BD,
故选:A.
4.
【分析】写出直线在x轴上方所对应的自变量的范围即可.
【解答】解:由图可知:当x>﹣2时,y>0,即kx+b>0,即﹣kx﹣b<0,
所以不等式﹣kx﹣b<0的解集为x>﹣2.
故选:A.
5.
【分析】根据众数、中位数、平均数、方差的计算方法分别进行计算即可.
【解答】解:将这20户的用水量从小到大排列,处在中间位置的两个数的平均数为4.5,因此选项A不符合题意;
这组数据的平均数为4.4(吨),因此选项B不符合题意;
这组数据出现次数最多的是5,共出现8次,所以用水量的众数是5,因此选项C符合题意;
这组数据的方差为[(3﹣4.4)2×4+(4﹣4.4)2×6+(5﹣4.4)2×8+(6﹣4.4)2×2]≈0.84,因此选项D不符合题意;
故选:C.
6.
【分析】根据平行四边形的性质,得到∠ABC=∠D=105°,AD=BC,进而得到CB=BE,∠BCE=∠BEC,设∠EAB的度数为x,列式计算即可.
【解答】解:∵ ABCD,∠D=105°,
∴∠ABC=∠D=105°,AD=BC,
∵AD=AE=BE,
∴∠EAB=∠EBA,CB=BE,
∴∠BCE=∠BEC,
设∠EAB的度数为x,则:∠EBA=x,∠CEB=∠EAB+∠EBA=2x,∠ACB=180°﹣∠ABC﹣∠CAB=75°﹣x,
∴2x=75°﹣x,
∴x=25°,
∴∠BAC=25°;
故选A.
7.
【分析】根据三角形的三边关系可求出n的范围,然后根据绝对值的性质以及二次根式的性质进行化简即可求出答案.
【解答】解:由三角形三边关系可知:3<n<7,
∴3﹣n<0,8﹣n>1,
原式=|3﹣n|+|8﹣n|
=﹣(3﹣n)+(8﹣n)
=﹣3+n+8﹣n
=5,
故选:A.
8.
【分析】根据勾股定理可以求得AC的长,再根据DA=DB,△BCD是直角三角形,由勾股定理即可求得BD的长,即可得到AD的长,然后即可计算出△ABD的面积.
【解答】解:∵∠C=90°,AB,CB=4,
∴AC8,
设AD=x,则CD=8﹣x,
∵∠C=90°,
∴BC2+CD2=BD2,
∴42+(8﹣x)2=x2,
解得x=5,
∴AD=5,
∴S△ABD10,
故选:C.
9.
【分析】根据图象数据直接分析B选项错误,进而求得甲队在2≤x≤6的时段内,y与x之间的函数关系式是y=75x+250;乙队在0≤x≤6的时段内,y与x之间的函数关系式是y=150x;得出甲队维修道路长度为550m时,乙队所维修的道路长度为600m,判断C选项,当x=2时,求得甲、乙两队所维修道路长度的差为100m,即可判断A选项,当x>2时,150x﹣(75x+250)=100,即可求得,继而判断D选项,即可求解.
【解答】解:由图象可得,
甲队开挖到400m时,用了2天,开挖6天时,甲队比乙队少挖了900﹣700=200(m),故B选项错误;
甲队在2≤x≤6的时段内,设y与x之间的函数关系式为y=kx+b,
∵点(2,400),(6,700))在该函数图象上,
;
解得,
即甲队在2≤x≤6的时段内,y与x之间的函数关系式是y=75x+250;
乙队在0≤x≤6的时段内,设y与x之间的函数关系式为y=ax,
∵点(6,900)在该函数图象上,
∴6a=900,
解得a=150,
即乙队在0≤x≤6的时段内,y与x之间的函数关系式是y=150x;
∴当75x+250=550,解得x=4,
在y=150x中,当x=4时,y=150×4=600
∴甲队维修道路长度为550m时,乙队所维修的道路长度为600m,故C选项错误;
当x=2时,甲、乙两队在施工过程中所挖河渠的长度相差400﹣150×2=100(m);故A选项错误
当x>2时,150x﹣(75x+250)=100,
解得;
即开工第2天或第..天时,甲、乙两队所维修道路长度的差为100m.故D选项正确,
故选:D.
10.
【分析】根据直角三角形斜边上的中线等于斜边的一半,可得FA=FC,根据等边三角形的性质可得EA=EC,根据线段垂直平分线的判定可得EF是线段AC的垂直平分线;根据条件及等边三角形的性质可得∠DFA=∠EAF=90°,DA⊥AC,从而得到DF∥AE,DA∥EF,可得到四边形ADFE为平行四边形而不是菱形;根据平行四边形的对角线互相平分可得AD=AB=2AF=4AG;易证DB=DA=EF,∠DBF=∠EFA=60°,BF=FA,即可得到△DBF≌△EFA.
【解答】解:连接FC,如图所示:
∵∠ACB=90°,F为AB的中点,
∴FA=FB=FC,
∵△ACE是等边三角形,
∴EA=EC,
∵FA=FC,EA=EC,
∴点F、点E都在线段AC的垂直平分线上,
∴EF垂直平分AC,即EF⊥AC;
∵△ABD和△ACE都是等边三角形,F为AB的中点,
∴DF⊥AB即∠DFA=90°,BD=DA=AB=2AF,∠DBA=∠DAB=∠EAC=∠ACE=60°.
∵∠BAC=30°,
∴∠DAC=∠EAF=90°,
∴∠DFA=∠EAF=90°,DA⊥AC,
∴DF∥AE,DA∥EF,
∴四边形ADFE为平行四边形而不是菱形;
∵四边形ADFE为平行四边形,
∴DA=EF,AF=2AG,
∴BD=DA=EF,DA=AB=2AF=4AG;
在△DBF和△EFA中,,
∴△DBF≌△EFA(SAS);
综上所述:①③④正确,
故选:C.
二、填空题
11.
【分析】根据一次函数的性质,可得答案.
【解答】解:∵一次函数y=(k﹣2)x+1的函数值y随x的增大而增大,
∴k﹣2>0,
解得k>2,
故答案为:k>2.
12.
【分析】根据勾股定理计算出AC的长度,进而求得该点与点A的距离,再根据点A表示的数为﹣1,可得该点表示的数.
【解答】解:在长方形ABCD中,AD=﹣1﹣(﹣4)=3,AB=CD=1,
∴,
则点A到该交点的距离为,
∵点A表示的数为﹣1,
∴该点表示的数为:,
故选:D.
13.
【分析】设点P的坐标为(m,m+1),利用两点间的距离结合PA=PB,即可得出关于m的一元一次方程,解之即可得出结论.
【解答】解:∵点P在直线yx+1上,
∴设点P的坐标为(m,m+1).
∵PA=PB,
∴(m﹣0)2+(m+1﹣4)2=(m﹣2)2+(m+1﹣4)2,
即4m﹣4=0,
解得:m=1,
∴点P的坐标为(1,).
故答案为:(1,).
14.
【分析】根据勾股定理得到BC5,由作图可知,MN是线段AC的垂直平分线,求得EC=EA,AF=CF,推出AE=CEBC=2.5,根据平行四边形的性质得到AD=BC=5,CD=AB=3,∠ACD=∠BAC=90°,同理证得AF=CF=2.5,于是得到结论.
【解答】解:∵AB⊥AC,AB=3,AC=4,
∴BC5,
由作图可知,MN是线段AC的垂直平分线,
∴EC=EA,AF=CF,
∴∠EAC=∠ACE,
∵∠B+∠ACB=∠BAE+∠CAE=90°,
∴∠B=∠BAE,
∴AE=BE,
∴AE=CEBC=2.5,
∵四边形ABCD是平行四边形,
∴AD=BC=5,CD=AB=3,∠ACD=∠BAC=90°,
同理证得AF=CF=2.5,
∴四边形AECF的周长=EC+EA+AF+CF=10,
故答案为:10.
15.
【分析】根据等腰直角三角形的性质得到OA1=1,OA2,OA3=()2,…,OA2020=()2019,再利用A1、A2、A3、…,每8个一循环,再回到x轴的负半轴的特点可得到点A2020在第一象限,即可确定点A2020的坐标.
【解答】解:∵等腰直角三角形OA1A2的直角边OA1在x轴的负半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3,以OA3为直角边作第三个等腰直角三角形OA3A4,…,
∴OA1=1,OA2,OA3=()2,…,OA2020=()2019,
∵A1、A2、A3、…,每8个一循环,再回到x轴的负半轴,
2022=8×252+6,
∴点A2022在第四象限,
∵OA2022=()2021,
∴点A2022的横坐标为:()2021=21010,纵坐标为﹣21010,
故答案为:(21010,﹣21010).
16.
【分析】利用坐标轴上点的坐标特征可求出A、B点的坐标,当△APQ是以AQ为底边的等腰三角形时,PA=PQ,根据等腰三角形的性质得∠PQA=∠PAQ,利用三角形外角性质和等量代换可得∠PQA=∠BPA,则BP=BA=10,所以OP=BP﹣OB=2,于是可得到此时P点坐标为(0,﹣2).
【解答】解:当y=0时,x+8=0,解得x=6,则A(6,0),
当x=0时,yx+8=8,则B(0,8),
∴AB10,
当△APQ是以AQ为底边的等腰三角形时,PA=PQ,
∴∠PQA=∠PAQ,
∵∠PQA=∠ABO+∠BPQ,∠APQ=∠ABO,
∴∠PQA=∠ABO+∠BPQ=∠APQ+∠BPQ=∠BPA,
∴∠PAQ=∠BPA,
∴BP=BA=10,
∴OP=BP﹣OB=2,
∴P(0,﹣2).
故答案为:(0,﹣2).
三、解答题
17.计算:(1)原式=2﹣2+1+1﹣2;
(2)原式23﹣4
=423﹣4
=21.
18.(1)证明:∵DE⊥AC,BF⊥AC,
∴∠AED=∠CFB=90°,
∵AD∥BC,
∴∠DAE=∠BCF,
在△DAE和△BCF中,
,
∴△DAE≌△BCF(ASA),
∴AD=CB,
∵AD∥BC,
∴四边形ABCD为平行四边形;
(2)解:∵四边形ABCD为平行四边形,
∴∠DAH=∠BCG,
AB∥CD,
∴∠CGB=∠GBA,
∵∠DAH=∠GBA,
∴∠CGB=∠BCG,
∴BG=BC,
在Rt△CFB中,
∵BF=BG﹣FG=BC﹣2,CF=4,
∴BC2=BF2+CF2,
∴BC2=(BC﹣2)2+42,
∴BC=5.
∴AD=BC=5.
19.(1)解:原式,
当时,
原式.
(2)解:∵x,y,
∴x﹣y=2,xy=3﹣5=﹣2,
∴2x2﹣5xy+2y2=2x2﹣4xy+2y2﹣xy=2(x﹣y)2﹣xy=2×(2)2﹣(﹣2)=42.
20.解:(1)由题意知,a=5,b=4,
中位数m81;
(2)根据上表统计显示,样本中的中位数和众数都是81,都落在“80≤x<120”内;
(3)1600=640(名),
答:估计课外阅读时间在“80≤x<120”内的学生有640名.
21.解:(1)连接AC,
∵AB=BC=AD=80m,∠ABC=90°
∴△ABC是等腰直角三角形,
∴AC80(m),∠CAB=45°,
∵CD=80m,
在△ACD中,AD2+AC2=802+(80)2=(80)2=CD2,
∴△ACD是直角三角形,
∴∠CAD=90°,
∴∠DAB=90°+45°=135°;
(2)过点D作DE⊥AB于E,作点A关于DE的对称点F,连接DF,
由轴对称的性质,得:DF=DA=80m,AE=EF,
由(1)知,∠BAD=135°,
∴∠DAE=45°,
∴△ADE是等腰直角三角形,
∴AE=DEAD=40(m),
∴AF=2AE=80(m),
∴被监控到的道路长度为80m.
22.解:(1)设每件A奖品的价格各是x元,每B奖品的价格各是y元,
根据题意得:,
解得,
答:每件A奖品的价格是16元,每件B奖品的价格是24元;
(2)根据题意得:w=16a+24(80﹣a)=﹣8a+1920,
∴w与a的函数关系式为w=﹣8a+1920(0<a<80);
(3)∵购买的A种奖品的数量不超过B种奖品数量的3倍,
∴a≤3(80﹣a),
解得a≤60,
在w=﹣8a+1920中,﹣8<0,
∴w随a的增大而减小,
∴a=75时,w最小,最小值为﹣8×60+1920=1440(元),
答:所需总费用的最小值是1440元.
23.解:(1)DF=AM,
证明,连接BD,
∵将线段ME绕点M逆时针60°得到线段MF,点E与点B重合,
∴MB=MF,∠BMF=60°,
∴△BMF为等边三角形,
∴∠FBM=60°,BM=BF,
∵菱形ABCD中,∠ABC=120°,
∴BC=CD,∠BCD=60°,
∴△BCD为等边三角形,
∴∠CBD=60°,BC=BD,
∴∠CBF=∠DBM,
∴△CBF≌△DBM(SAS),
∴CF=DM,
∵CD=AD,
∴DF=AM;
(2)结论:BE+AM=DF.
证明:如图2,过点M作MN∥AB交DB的延长线于点N,
∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC=120°,
∴∠BAD=60°,
∴△ABD是等边三角形,
∴BD=AB=AD,∠DAB=∠ABD=60°,
∵MN∥AB,
∴∠N=∠ABD=60°,∠NMD=∠BAD=60°,
∴△MND是等边三角形,
∴MN=MD=DN,
∵ME=MF,∠MEF=60°,
∴△MEF是等边三角形,
∴ME=MF,∠EMF=60°,
∴∠NME=∠DMF,
∴△MNE≌△MDF(SAS),
∴EN=DF,
即BE+BN=DF,
∵MD=DN,AD=BD,
∴AM=BN,
∴BE+AM=DF.
(3)如图3,当点E在线段BD上时,
由(2)可知BE+AM=DF.
∵AB=6,
∴AB=BD=6,
∵AD=3AM,BD=2BE,
∴AM=2,BE=3,
∴DF=2+3=5;
如图4,当点E在DB的延长线上时,
则△DMN和△EFM都是等边三角形,
同(2)可证△MNE≌△MDF(SAS),
∴EN=DF,
∵MN=DM=DN,
∴AM=BN,
∴AM+DF=BE,
∵AM=2,BE=3,
∴DF=3﹣2=1.
综合以上可得DF的长为5或1.
24.解:(1)当x=0时,代入yx+b得,y=b,D点坐标(0,b),OD=b,
∵OD=BE,
∴BE=b,
点E的坐标为(2,3﹣b),代入yx+b得:3﹣b=﹣1+b,
解得:b=2;
(2)∵S四边形OAED3,
三角形ODM的面积与四边形OAEM的面积之比为1:3,设点M的横坐标为m,
①当点M在线段DE上时,
S△ODM,则m,
解得m,代入y2得,y,此时点M(,),
②当点M在线段ED的延长线上时,
S△ODB,则,
解得m,代入y2得,y,此时点M(,),
∴M(,)或(,);
(3)①当OD为菱形对角线时,如图,点M的纵坐标是1,
当y=1时,代入y2得,x=2,
则点M的坐标是(2,1),
∵四边形OMDN是菱形,
∴点M,N关于y轴对称,
∴点N的坐标为(﹣2,1);
②当OM为菱形对角线时,如图,则DM=DO=2,
设M(m,m+2),由两点间距离公式可得,
∴(m﹣0)2+(m+2﹣2)2=22,
解得:m或m,
∴M(,2)或M(,2),
∵MN=OD=2,
∴N(,)或N(,);
③当DM为菱形对角线时,如图,则MO=DO=2,
同理:(m﹣0)2+(m+2)2=22,
解得:m=0(舍去)或m,
∴M(,),
∵MN=OD=2,
∴N(,),
综上所述:点N的坐标为(﹣2,1)或(,)或(,)或(,).
一、选择题(共8题,每小题3分,共24分)
1.函数的自变量x的取值范围是( )
A.x≠2 B.x≥2 C.x<0 D.x>2
2.下列各式计算错误的是( )
A. B.
C. D.
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,添加下列条件,能使菱形ABCD成为正方形的是( )
A.AC=BD B.AC⊥BD C.AD=AB D.AC平分∠DAB
4.如图,直线y=kx+b交坐标轴于A(﹣2,0),B(0,1)两点,则不等式﹣kx﹣b<0的解集为( )
A.x>﹣2 B.x<﹣2 C.x>2 D.x<2
5.为了了解某小区居民的用水情况,随机抽查了若干户家庭的某月用水量,统计结果如表所示:
月用水量/吨 3 4 5 6
户数 4 6 8 2
关于这若干户家庭的该月用水量的数据统计分析,下列说法正确的是( )
A.中位数是5 B.平均数是7 C.众数是5 D.方差是1
6.如图,AC是 ABCD的对角线,点E在AC上,AD=AE=BE,∠D=105°,则∠BAC是( )
A.25° B.30° C.45° D.50°
7.若2、5、n为三角形的三边长,则化简的结果为( )
A.5 B.2n﹣11 C.11﹣2n D.﹣5
8.如图,在Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB,AB,CB=4,则△ABD的面积为( )
A.6 B.7 C.10 D.9
9.甲、乙两个工程队分别同时维修两段道路,所维修的道路长度与维修的天数之间的函数关系图象如图所示,下列结论正确的是( )
A.开工第2天时,甲队比乙队多维修200m
B.开工第6天时,甲队比乙队多维修200m
C.甲队维修道路长度为550m时,乙队所维修的道路长度为650m
D.开工第2天或第天时,甲、乙两队所维修道路长度的差为100m
10.如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.则正确结论的序号是( )
A.①③ B.②④ C.①③④ D.②③④
二、填空题(共8小题,每小题3分,共24分)
11.若一次函数y=(k﹣2)x+1的函数值y随x的增大而增大,则k的取值范围是 .
12.如图,长方形ABCD的边AD在数轴上,若点A与数轴上表示数﹣1的点重合,点D与数轴上表示数﹣4的点重合,AB=1,以点A为圆心,对角线AC的长为半径作弧与数轴负半轴交于一点E,则点E表示的数为 .
13.如图,点A(0,4),B(2,4),点P在直线 yx+1上,当PA=PB时,点P的坐标是 .
14.如图,在平行四边形ABCD中,AB⊥AC,AB=3,AC=4,分别以A,C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,过M,N两点作直线,与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为 .
15.如图,在平面直角坐标系中,点A1的坐标为(﹣1,0),以OA1为直角边作等腰Rt△OA2A3,再以OA3为直角边作等腰Rt△OA3A4,…,按此规律进行下去,则点A2022的坐标为 .
16.如图,一次函数yx+8的图象与x,y轴交于点A,B,点B关于x轴的对称点为C,动点P,Q分别在线段BC,AB上(P不与B,C重合),且∠APQ=∠ABO,当△APQ是以AQ为底边的等腰三角形时,点P的坐标是 .
三、解答题(本大题共8小题,满分共72分)
17.(每小题4分,共8分)计算:
(1);
(2).
18.已知:如图,在四边形ABCD中,DE⊥AC,BF⊥AC,垂足分别为E,F,延长DE、BF,分别交AB于点H,交BC于点G,若AD∥BC,AE=CF.
(1)求证:四边形ABCD为平行四边形;
(2)若∠DAH=∠GBA,GF=2,CF=4,求AD的长.
19.(每小题4分,共8分)(1)先化简,再求值:,其中.
(2)已知,,试求代数式2x2﹣5xy+2y2的值.
20.(8分)收集数据:4月23日是世界读书日,某校为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:min)
30 60 81 50 40 110 130 146 90 100
60 81 120 140 70 81 10 20 100 81
整理数据:
课外阅读时间x 0≤x<40 40≤x<80 80≤x<120 120≤x<160
人数 3 a 8 b
分析数据:
平均数 中位数 众数
80 m 81
解决问题:
(1)直接写出a,b,m的值;
(2)样本中的中位数和众数落在哪个范围内?
(3)该校现有学生1600人,估计课外阅读时间在“80≤x<120”内的学生有多少名?
21.(8分)如图,四边形ABCD为某工厂的平面图,经测量AB=BC=AD=80m,CD=80m,且∠ABC=90°.
(1)求∠DAB的度数;
(2)若直线AB为工厂的车辆进出口道路(道路的宽度忽略不计),工作人员想要在点D处安装一个摄像头观察车辆进出工厂的情况,已知摄像头能监控的最远距离为80m,求被监控到的道路长度为多少m?
22.(10分)为了提高同学们学习数学的兴趣,某中学开展主题为“感受数学
魅力,享受数学乐趣”的数学活动.并计划购买A、B两种奖品奖励在数学活动中表现突出的学生,已知购买1件A种奖品和2件B种奖品共需64元,购买2件A种奖品和1件B种奖品共需56元.
(1)每件A、B奖品的价格各是多少元?
(2)根据需要,该学校准备购买A、B两种奖品共80件,设购买a件A种奖品,所需总费用为w元,求w与a的函数关系式,并直接写出a的取值范围;
(3)在(2)的条件下,若要求购买的A种奖品的数量不超过B种奖品数量的3倍,求所需总费用的最小值.
23.(10分)在菱形ABCD中,∠ABC=120°,点M在DA的延长线上,点E是直线BD上的动点,连接ME,将线段ME绕点M逆时针旋转60°得到线段MF,连接EF,DF.
(1)如图①,当点E与点B重合时,请直接写出线段AM与DF的数量关系;
(2)如图②,当点E在BD上时,请写出线段BE,AM,DF之间的数量关系,并给出证明;
(3)当点E在直线BD上时,若AB=6,AD=3AM,BD=2BE,请直接写出线段DF的长.
24.(12分)如图,矩形OABC的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标为(2,3),一次函数yx+b的图象与边OC、AB分别交于点D、E,且OD=BE.点M是直线DE上的一个动点.
(1)求b的值;
(2)连结OM,若三角形ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;
(3)设点N是平面内的一点,以O、D、M、N为顶点的四边形是菱形,直接写出N的坐标.
答案
一、选择题
1.根据二次根式有意义的条件成立不等式,解不等式得到答案.
【解答】解:由题意得:x﹣2≥0,
解得:x≥2,
故选:B.
2.
【分析】根据合并同类二次根式的法则、二次根式的乘法、平方差公式及二次根式的除法分别计算可得.
【解答】解:A、43,此选项计算正确;
B、,此选项计算正确;
C、()2﹣()2=3﹣2=1,此选项计算错误;
D、3,此选项计算正确;
故选:C.
3.
【分析】根据菱形的性质及正方形的判定来添加合适的条件.
【解答】解:要使菱形成为正方形,只要菱形满足以下条件之一即可:
(1)有一个内角是直角,(2)对角线相等,
即∠ABC=90°或AC=BD,
故选:A.
4.
【分析】写出直线在x轴上方所对应的自变量的范围即可.
【解答】解:由图可知:当x>﹣2时,y>0,即kx+b>0,即﹣kx﹣b<0,
所以不等式﹣kx﹣b<0的解集为x>﹣2.
故选:A.
5.
【分析】根据众数、中位数、平均数、方差的计算方法分别进行计算即可.
【解答】解:将这20户的用水量从小到大排列,处在中间位置的两个数的平均数为4.5,因此选项A不符合题意;
这组数据的平均数为4.4(吨),因此选项B不符合题意;
这组数据出现次数最多的是5,共出现8次,所以用水量的众数是5,因此选项C符合题意;
这组数据的方差为[(3﹣4.4)2×4+(4﹣4.4)2×6+(5﹣4.4)2×8+(6﹣4.4)2×2]≈0.84,因此选项D不符合题意;
故选:C.
6.
【分析】根据平行四边形的性质,得到∠ABC=∠D=105°,AD=BC,进而得到CB=BE,∠BCE=∠BEC,设∠EAB的度数为x,列式计算即可.
【解答】解:∵ ABCD,∠D=105°,
∴∠ABC=∠D=105°,AD=BC,
∵AD=AE=BE,
∴∠EAB=∠EBA,CB=BE,
∴∠BCE=∠BEC,
设∠EAB的度数为x,则:∠EBA=x,∠CEB=∠EAB+∠EBA=2x,∠ACB=180°﹣∠ABC﹣∠CAB=75°﹣x,
∴2x=75°﹣x,
∴x=25°,
∴∠BAC=25°;
故选A.
7.
【分析】根据三角形的三边关系可求出n的范围,然后根据绝对值的性质以及二次根式的性质进行化简即可求出答案.
【解答】解:由三角形三边关系可知:3<n<7,
∴3﹣n<0,8﹣n>1,
原式=|3﹣n|+|8﹣n|
=﹣(3﹣n)+(8﹣n)
=﹣3+n+8﹣n
=5,
故选:A.
8.
【分析】根据勾股定理可以求得AC的长,再根据DA=DB,△BCD是直角三角形,由勾股定理即可求得BD的长,即可得到AD的长,然后即可计算出△ABD的面积.
【解答】解:∵∠C=90°,AB,CB=4,
∴AC8,
设AD=x,则CD=8﹣x,
∵∠C=90°,
∴BC2+CD2=BD2,
∴42+(8﹣x)2=x2,
解得x=5,
∴AD=5,
∴S△ABD10,
故选:C.
9.
【分析】根据图象数据直接分析B选项错误,进而求得甲队在2≤x≤6的时段内,y与x之间的函数关系式是y=75x+250;乙队在0≤x≤6的时段内,y与x之间的函数关系式是y=150x;得出甲队维修道路长度为550m时,乙队所维修的道路长度为600m,判断C选项,当x=2时,求得甲、乙两队所维修道路长度的差为100m,即可判断A选项,当x>2时,150x﹣(75x+250)=100,即可求得,继而判断D选项,即可求解.
【解答】解:由图象可得,
甲队开挖到400m时,用了2天,开挖6天时,甲队比乙队少挖了900﹣700=200(m),故B选项错误;
甲队在2≤x≤6的时段内,设y与x之间的函数关系式为y=kx+b,
∵点(2,400),(6,700))在该函数图象上,
;
解得,
即甲队在2≤x≤6的时段内,y与x之间的函数关系式是y=75x+250;
乙队在0≤x≤6的时段内,设y与x之间的函数关系式为y=ax,
∵点(6,900)在该函数图象上,
∴6a=900,
解得a=150,
即乙队在0≤x≤6的时段内,y与x之间的函数关系式是y=150x;
∴当75x+250=550,解得x=4,
在y=150x中,当x=4时,y=150×4=600
∴甲队维修道路长度为550m时,乙队所维修的道路长度为600m,故C选项错误;
当x=2时,甲、乙两队在施工过程中所挖河渠的长度相差400﹣150×2=100(m);故A选项错误
当x>2时,150x﹣(75x+250)=100,
解得;
即开工第2天或第..天时,甲、乙两队所维修道路长度的差为100m.故D选项正确,
故选:D.
10.
【分析】根据直角三角形斜边上的中线等于斜边的一半,可得FA=FC,根据等边三角形的性质可得EA=EC,根据线段垂直平分线的判定可得EF是线段AC的垂直平分线;根据条件及等边三角形的性质可得∠DFA=∠EAF=90°,DA⊥AC,从而得到DF∥AE,DA∥EF,可得到四边形ADFE为平行四边形而不是菱形;根据平行四边形的对角线互相平分可得AD=AB=2AF=4AG;易证DB=DA=EF,∠DBF=∠EFA=60°,BF=FA,即可得到△DBF≌△EFA.
【解答】解:连接FC,如图所示:
∵∠ACB=90°,F为AB的中点,
∴FA=FB=FC,
∵△ACE是等边三角形,
∴EA=EC,
∵FA=FC,EA=EC,
∴点F、点E都在线段AC的垂直平分线上,
∴EF垂直平分AC,即EF⊥AC;
∵△ABD和△ACE都是等边三角形,F为AB的中点,
∴DF⊥AB即∠DFA=90°,BD=DA=AB=2AF,∠DBA=∠DAB=∠EAC=∠ACE=60°.
∵∠BAC=30°,
∴∠DAC=∠EAF=90°,
∴∠DFA=∠EAF=90°,DA⊥AC,
∴DF∥AE,DA∥EF,
∴四边形ADFE为平行四边形而不是菱形;
∵四边形ADFE为平行四边形,
∴DA=EF,AF=2AG,
∴BD=DA=EF,DA=AB=2AF=4AG;
在△DBF和△EFA中,,
∴△DBF≌△EFA(SAS);
综上所述:①③④正确,
故选:C.
二、填空题
11.
【分析】根据一次函数的性质,可得答案.
【解答】解:∵一次函数y=(k﹣2)x+1的函数值y随x的增大而增大,
∴k﹣2>0,
解得k>2,
故答案为:k>2.
12.
【分析】根据勾股定理计算出AC的长度,进而求得该点与点A的距离,再根据点A表示的数为﹣1,可得该点表示的数.
【解答】解:在长方形ABCD中,AD=﹣1﹣(﹣4)=3,AB=CD=1,
∴,
则点A到该交点的距离为,
∵点A表示的数为﹣1,
∴该点表示的数为:,
故选:D.
13.
【分析】设点P的坐标为(m,m+1),利用两点间的距离结合PA=PB,即可得出关于m的一元一次方程,解之即可得出结论.
【解答】解:∵点P在直线yx+1上,
∴设点P的坐标为(m,m+1).
∵PA=PB,
∴(m﹣0)2+(m+1﹣4)2=(m﹣2)2+(m+1﹣4)2,
即4m﹣4=0,
解得:m=1,
∴点P的坐标为(1,).
故答案为:(1,).
14.
【分析】根据勾股定理得到BC5,由作图可知,MN是线段AC的垂直平分线,求得EC=EA,AF=CF,推出AE=CEBC=2.5,根据平行四边形的性质得到AD=BC=5,CD=AB=3,∠ACD=∠BAC=90°,同理证得AF=CF=2.5,于是得到结论.
【解答】解:∵AB⊥AC,AB=3,AC=4,
∴BC5,
由作图可知,MN是线段AC的垂直平分线,
∴EC=EA,AF=CF,
∴∠EAC=∠ACE,
∵∠B+∠ACB=∠BAE+∠CAE=90°,
∴∠B=∠BAE,
∴AE=BE,
∴AE=CEBC=2.5,
∵四边形ABCD是平行四边形,
∴AD=BC=5,CD=AB=3,∠ACD=∠BAC=90°,
同理证得AF=CF=2.5,
∴四边形AECF的周长=EC+EA+AF+CF=10,
故答案为:10.
15.
【分析】根据等腰直角三角形的性质得到OA1=1,OA2,OA3=()2,…,OA2020=()2019,再利用A1、A2、A3、…,每8个一循环,再回到x轴的负半轴的特点可得到点A2020在第一象限,即可确定点A2020的坐标.
【解答】解:∵等腰直角三角形OA1A2的直角边OA1在x轴的负半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3,以OA3为直角边作第三个等腰直角三角形OA3A4,…,
∴OA1=1,OA2,OA3=()2,…,OA2020=()2019,
∵A1、A2、A3、…,每8个一循环,再回到x轴的负半轴,
2022=8×252+6,
∴点A2022在第四象限,
∵OA2022=()2021,
∴点A2022的横坐标为:()2021=21010,纵坐标为﹣21010,
故答案为:(21010,﹣21010).
16.
【分析】利用坐标轴上点的坐标特征可求出A、B点的坐标,当△APQ是以AQ为底边的等腰三角形时,PA=PQ,根据等腰三角形的性质得∠PQA=∠PAQ,利用三角形外角性质和等量代换可得∠PQA=∠BPA,则BP=BA=10,所以OP=BP﹣OB=2,于是可得到此时P点坐标为(0,﹣2).
【解答】解:当y=0时,x+8=0,解得x=6,则A(6,0),
当x=0时,yx+8=8,则B(0,8),
∴AB10,
当△APQ是以AQ为底边的等腰三角形时,PA=PQ,
∴∠PQA=∠PAQ,
∵∠PQA=∠ABO+∠BPQ,∠APQ=∠ABO,
∴∠PQA=∠ABO+∠BPQ=∠APQ+∠BPQ=∠BPA,
∴∠PAQ=∠BPA,
∴BP=BA=10,
∴OP=BP﹣OB=2,
∴P(0,﹣2).
故答案为:(0,﹣2).
三、解答题
17.计算:(1)原式=2﹣2+1+1﹣2;
(2)原式23﹣4
=423﹣4
=21.
18.(1)证明:∵DE⊥AC,BF⊥AC,
∴∠AED=∠CFB=90°,
∵AD∥BC,
∴∠DAE=∠BCF,
在△DAE和△BCF中,
,
∴△DAE≌△BCF(ASA),
∴AD=CB,
∵AD∥BC,
∴四边形ABCD为平行四边形;
(2)解:∵四边形ABCD为平行四边形,
∴∠DAH=∠BCG,
AB∥CD,
∴∠CGB=∠GBA,
∵∠DAH=∠GBA,
∴∠CGB=∠BCG,
∴BG=BC,
在Rt△CFB中,
∵BF=BG﹣FG=BC﹣2,CF=4,
∴BC2=BF2+CF2,
∴BC2=(BC﹣2)2+42,
∴BC=5.
∴AD=BC=5.
19.(1)解:原式,
当时,
原式.
(2)解:∵x,y,
∴x﹣y=2,xy=3﹣5=﹣2,
∴2x2﹣5xy+2y2=2x2﹣4xy+2y2﹣xy=2(x﹣y)2﹣xy=2×(2)2﹣(﹣2)=42.
20.解:(1)由题意知,a=5,b=4,
中位数m81;
(2)根据上表统计显示,样本中的中位数和众数都是81,都落在“80≤x<120”内;
(3)1600=640(名),
答:估计课外阅读时间在“80≤x<120”内的学生有640名.
21.解:(1)连接AC,
∵AB=BC=AD=80m,∠ABC=90°
∴△ABC是等腰直角三角形,
∴AC80(m),∠CAB=45°,
∵CD=80m,
在△ACD中,AD2+AC2=802+(80)2=(80)2=CD2,
∴△ACD是直角三角形,
∴∠CAD=90°,
∴∠DAB=90°+45°=135°;
(2)过点D作DE⊥AB于E,作点A关于DE的对称点F,连接DF,
由轴对称的性质,得:DF=DA=80m,AE=EF,
由(1)知,∠BAD=135°,
∴∠DAE=45°,
∴△ADE是等腰直角三角形,
∴AE=DEAD=40(m),
∴AF=2AE=80(m),
∴被监控到的道路长度为80m.
22.解:(1)设每件A奖品的价格各是x元,每B奖品的价格各是y元,
根据题意得:,
解得,
答:每件A奖品的价格是16元,每件B奖品的价格是24元;
(2)根据题意得:w=16a+24(80﹣a)=﹣8a+1920,
∴w与a的函数关系式为w=﹣8a+1920(0<a<80);
(3)∵购买的A种奖品的数量不超过B种奖品数量的3倍,
∴a≤3(80﹣a),
解得a≤60,
在w=﹣8a+1920中,﹣8<0,
∴w随a的增大而减小,
∴a=75时,w最小,最小值为﹣8×60+1920=1440(元),
答:所需总费用的最小值是1440元.
23.解:(1)DF=AM,
证明,连接BD,
∵将线段ME绕点M逆时针60°得到线段MF,点E与点B重合,
∴MB=MF,∠BMF=60°,
∴△BMF为等边三角形,
∴∠FBM=60°,BM=BF,
∵菱形ABCD中,∠ABC=120°,
∴BC=CD,∠BCD=60°,
∴△BCD为等边三角形,
∴∠CBD=60°,BC=BD,
∴∠CBF=∠DBM,
∴△CBF≌△DBM(SAS),
∴CF=DM,
∵CD=AD,
∴DF=AM;
(2)结论:BE+AM=DF.
证明:如图2,过点M作MN∥AB交DB的延长线于点N,
∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC=120°,
∴∠BAD=60°,
∴△ABD是等边三角形,
∴BD=AB=AD,∠DAB=∠ABD=60°,
∵MN∥AB,
∴∠N=∠ABD=60°,∠NMD=∠BAD=60°,
∴△MND是等边三角形,
∴MN=MD=DN,
∵ME=MF,∠MEF=60°,
∴△MEF是等边三角形,
∴ME=MF,∠EMF=60°,
∴∠NME=∠DMF,
∴△MNE≌△MDF(SAS),
∴EN=DF,
即BE+BN=DF,
∵MD=DN,AD=BD,
∴AM=BN,
∴BE+AM=DF.
(3)如图3,当点E在线段BD上时,
由(2)可知BE+AM=DF.
∵AB=6,
∴AB=BD=6,
∵AD=3AM,BD=2BE,
∴AM=2,BE=3,
∴DF=2+3=5;
如图4,当点E在DB的延长线上时,
则△DMN和△EFM都是等边三角形,
同(2)可证△MNE≌△MDF(SAS),
∴EN=DF,
∵MN=DM=DN,
∴AM=BN,
∴AM+DF=BE,
∵AM=2,BE=3,
∴DF=3﹣2=1.
综合以上可得DF的长为5或1.
24.解:(1)当x=0时,代入yx+b得,y=b,D点坐标(0,b),OD=b,
∵OD=BE,
∴BE=b,
点E的坐标为(2,3﹣b),代入yx+b得:3﹣b=﹣1+b,
解得:b=2;
(2)∵S四边形OAED3,
三角形ODM的面积与四边形OAEM的面积之比为1:3,设点M的横坐标为m,
①当点M在线段DE上时,
S△ODM,则m,
解得m,代入y2得,y,此时点M(,),
②当点M在线段ED的延长线上时,
S△ODB,则,
解得m,代入y2得,y,此时点M(,),
∴M(,)或(,);
(3)①当OD为菱形对角线时,如图,点M的纵坐标是1,
当y=1时,代入y2得,x=2,
则点M的坐标是(2,1),
∵四边形OMDN是菱形,
∴点M,N关于y轴对称,
∴点N的坐标为(﹣2,1);
②当OM为菱形对角线时,如图,则DM=DO=2,
设M(m,m+2),由两点间距离公式可得,
∴(m﹣0)2+(m+2﹣2)2=22,
解得:m或m,
∴M(,2)或M(,2),
∵MN=OD=2,
∴N(,)或N(,);
③当DM为菱形对角线时,如图,则MO=DO=2,
同理:(m﹣0)2+(m+2)2=22,
解得:m=0(舍去)或m,
∴M(,),
∵MN=OD=2,
∴N(,),
综上所述:点N的坐标为(﹣2,1)或(,)或(,)或(,).
同课章节目录
