人教版九年级数学下册 第二十六章 反比例函数 单元测试卷(含详解)
文档属性
| 名称 | 人教版九年级数学下册 第二十六章 反比例函数 单元测试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1000.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-04 19:10:43 | ||
图片预览



文档简介
第二十六章《反比例函数》单元测试卷
一、单选题(30分)
1.若反比例函数的图象经过点,则m的值是( )
A.4 B. C.2 D.
2.下列函数:①,②,③,④,⑤,⑥,⑦,⑧.其中是的反比例函数的有( )
A.1个 B.2个 C.3个 D.4个
3.已知反比例函数的图象经过点,则此反比例函数的图象在( )
A.第一、二象限 B.第一、三象限 C.第二、四象限 D.第三、四象限
4.如图,的三个顶点分别为,,,若反比例函数的图像与有交点,则的取值范围是( ).
A. B. C. D.
5.如图,在平面直角坐标系中,反比例函数(k为常数)的图像与正比例函数的图像交于A、B两点,若,则k的值为( )
A.4 B. C. D.1
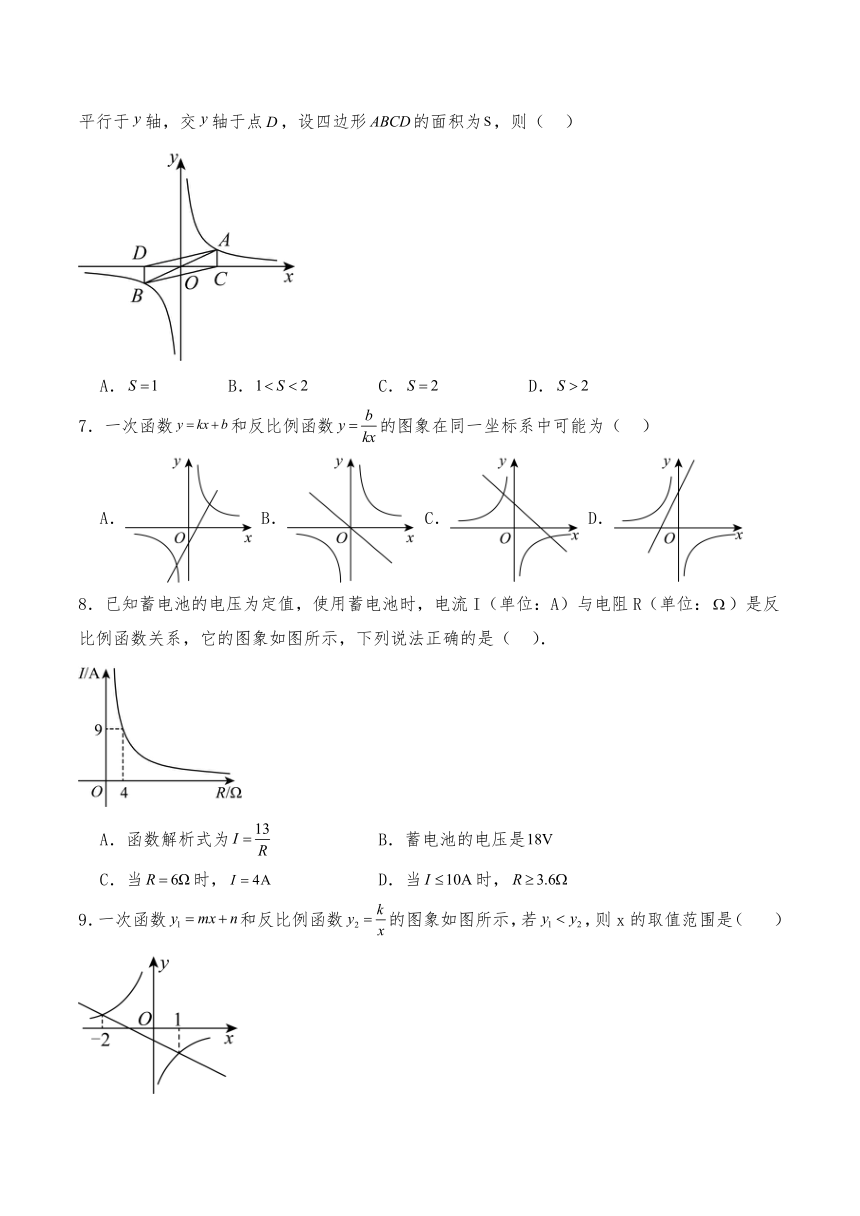
6.点,是反比例函数上关于原点对称的任意两点,平行于轴,交轴于点,平行于轴,交轴于点,设四边形的面积为,则( )
A. B. C. D.
7.一次函数和反比例函数的图象在同一坐标系中可能为( )
A. B. C. D.
8.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示,下列说法正确的是( ).
A.函数解析式为 B.蓄电池的电压是
C.当时, D.当时,
9.一次函数和反比例函数的图象如图所示,若,则x的取值范围是( )
A.或 B.或 C.或 D.
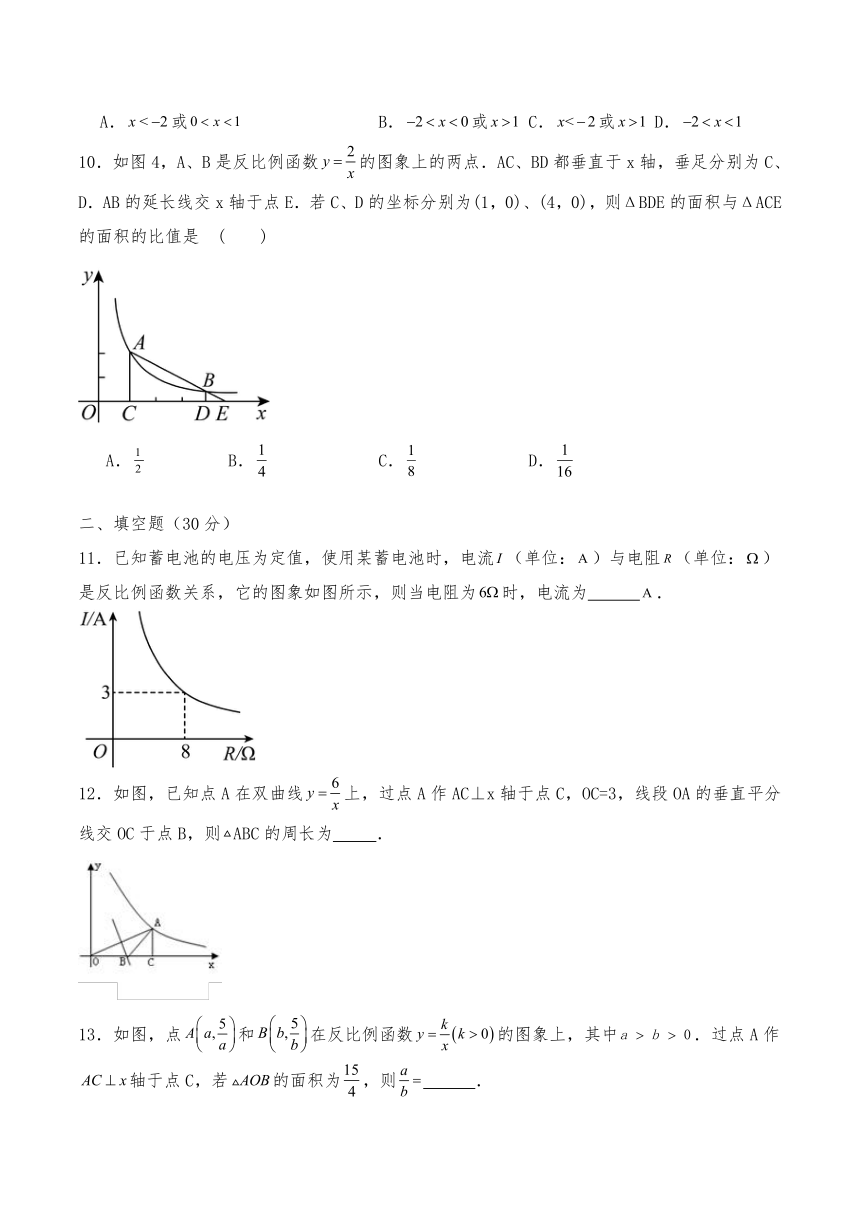
10.如图4,A、B是反比例函数的图象上的两点.AC、BD都垂直于x轴,垂足分别为C、D.AB的延长线交x轴于点E.若C、D的坐标分别为(1,0)、(4,0),则ΔBDE的面积与ΔACE的面积的比值是 ( )
A. B. C. D.
二、填空题(30分)
11.已知蓄电池的电压为定值,使用某蓄电池时,电流(单位:)与电阻(单位:)是反比例函数关系,它的图象如图所示,则当电阻为时,电流为 .
12.如图,已知点A在双曲线上,过点A作AC⊥x轴于点C,OC=3,线段OA的垂直平分线交OC于点B,则ABC的周长为 .
13.如图,点和在反比例函数的图象上,其中.过点A作轴于点C,若的面积为,则 .
14.反比例函数与正比例函数的图像没有交点,则k的取值范围为 .
15.设函数与的图象的交点坐标为,则的值为 .
16.在反比例函数中,当时函数的值为 .
17.若反比例函数的图像经过点和点,则
18.如图,在平面直角坐标系中,矩形的面积为,顶点A、C分别在x轴,y轴上,顶点B在第三象限,对角线交于点D.若反比例函数的图象经过点D,则k的值为 .
19.若点,,都在反比例函数(k为常数)的图像上,则,,的大小关系为 .(用“”连接)
20.如图,在平面直角坐标系中,正方形的顶点的坐标为,点在轴正半轴上,点在双曲线上,过点作轴交双曲线于点,则长为 .
三、解答题(60分)
21.如图,反比例函数(k为常数,且k≠0)经过点A(1,3).
(1)求反比例函数的解析式;
(2)在x轴正半轴上有一点B,若△AOB的面积为6,求直线AB的解析式.
22.已知反比例函数y=,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
23.已知如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A、B两点,A点坐标是(﹣2,1),B点坐标(1,n);
(1)求出k,b,m,n的值;
(2)求△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值的x的取值范围.
24.在李村河治理工程实验过程中,某工程队接受一项开挖水渠的工程,所需天数(天)与每天完成的工程量(天)的函数关系图象如图所示,是双曲线的一部分.
请根据题意,求与之间的函数表达式;
若该工程队有台挖掘机,每台挖掘机每天能够开挖水渠米,问该工程队需用多少天才能完成此项任务?
如果为了防汛工作的紧急需要,必须在一个月内(按天计算)完成任务,那么每天至少要完成多少米?
25.受新冠肺炎疫情的影响,某化工厂从2022年1月开始产量下降.借此机会,为了贯彻“发展循环经济,提高工厂效益”的绿色发展理念;管理人员对生产线进行为期5个月的升级改造,改造期间的月利润与时间成反比例函数;从6月初开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2022年1月为第1个月,第x(x为正整数)个月的利润为y万元,其图象如图所示,试解决下列问题:
(1)分别直接写出该化工厂对生产线进行升级改造前后,y与x的函数表达式,并写出自变量范围;
(2)到第几个月时,该化工厂月利润才能再次达到100万元?
(3)当月利润少于50万元时,为该化工厂的资金紧张期,问该化工厂资金紧张期共有几个月?
26.近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是.在一次矿难事件的调查中发现:从零时起,井内空气中的浓度达到,此后浓度呈直线型增加,在第7小时达到最高值,发生爆炸;爆炸后,空气中的浓度成反比例下降.如图,根据题中相关信息回答下列问题:
(1)求爆炸前后空气中浓度与时间的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的浓度达到时,井下的矿工接到自动报警信号,这时他们至少要以多少的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的浓度降到及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?
27.如图,已知直线y=x与双曲线y=(k>0)交于A、B两点,且点A的横坐标为6
(1)求k的值;
(2)若双曲线y=(k>0)上一点C的纵坐标为9,求△AOC的面积;
(3)过原点O的另一条直线l交双曲线y=(k>0)于P、Q两点(P点在第一象限),若由点A、B、P、Q为顶点组成的四边形面积为96,求点P的坐标.
答案
一、单选题
1.B
【分析】根据反比例函数图象上点的坐标特征得到,然后解关于m的方程即可.
【详解】解:∵反比例函数的图象经过点,
∴,
∴.
故选B.
2.C
【分析】根据反比例的三种形式判断即可.
【详解】解:反比例的三种形式分别为:,,.
①中的次数是,是一次函数,不是反比例函数;
②,③是反比例函数;
④中分母是,故不是反比例函数;
⑤是反比例函数;
⑥中没有,故不是反比例函数;
⑦分母是,故不是反比例函数;
⑧中的次数是,是一次函数,不是反比例函数.
故有三个是反比例函数.
故选C.
3.C
【分析】本题考查了反比例函数的图象分布,根据题意,得,选择即可,熟练掌握图象分布的条件是解题的关键.
【详解】∵反比例函数的图象经过点,
∴,
故图象分布在第二、四象限,
故选C.
4.B
【分析】根据题意,先求得反比例函数图像经过点C时的k值,再求解直线的解析式,然后求得直线与反比例函数图像有相切于一点的k值,进而可求解.
【详解】解:由反比例函数的图像与有交点知,
当反比例函数的图像经过点时,则有,
当反比例函数的图像经过点时,则有,
此时反比例函数为,则点也在此反比例函数图像上,
设直线的解析式为,
将、代入,得,
解得,
∴直线的解析式为,
联立方程组,整理得,
由得,此时直线与反比例函数的图像相切于一点,
故当时,反比例函数的图像与有交点,
故选:B.
5.D
【分析】根据反比例函数与正比例函数的图像关于原点对称,设,则,根据勾股定理求得的长度,根据,求得的值,进而即可求解.
【详解】解:∵反比例函数(k为常数)的图像与正比例函数的图像交于A、B两点,
∴设,则,,
则,
,
,
解得(负值舍去),
,
,
故选D.
6.C
【分析】根据过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积可知,,再根据反比例函数的对称性可知,为中点,则,,进而求出四边形的面积.
【详解】解:,是函数的图象上关于原点对称的任意两点,且平行于轴,平行于轴,
,
假设点坐标为,则点坐标为,
则,
,,
四边形面积.
故选:C
7.C
【分析】此题考查反比例函数和一次函数的图象共存问题;结合图象分别分析一次函数与反比例函数中,的符号,得出一致的符合题意,得出矛盾的不符合题意,从而可得答案.
【详解】解:A选项:由反比例函数的性质知k、b同号,由一次函数图象得,,得k、b异号.两者不一致,故A不符合题意;
B选项:由反比例函数的性质知k、b同号,由一次函数图象得,,两者不一致,故B不符合题意;
C选项:由反比例函数的性质知k、b异号,由一次函数图象得,,k、b异号,两者一致,故C符合题意;
D选项:由反比例函数的性质知k、b异号,由一次函数图象得,,k、b同号,两者不一致.故D不符合题意;
故选C
8.D
【分析】根据反比例函数图象,并结合物理学科中的电流等于电压除以电阻的知识点即可求解.
【详解】解:设,
∵图象过,
∴,
∵,
∴蓄电池的电压是,
∴选项A、B错误,不符合题意;
当时,,
∴选项C错误,不符合题意;
当时,,
由图象可知:当时,,
∴选项D正确,符合题意,
故选:D.
9.B
【分析】此题考查了根据反比例函数和一次函数图形,求出自变量取值范围,根据图象,找出使一次函数图象低于反比例函数图象时自变量的取值范围即可.
【详解】解:由图可知,当或时,,
故选:B.
10.D
【分析】根据函数解析式求得AC=2,BD=,再证明△BDE∽△ACE,根据相似三角形的性质即可求解.
【详解】解:∵C、D的坐标分别为(1,0),(4,0),
∴AC=2,BD=,
∵AC⊥CD,BD⊥CD,
∴∠ACD=∠BDE=90°,
∴,
∴△BDE∽△ACE,
∴△BDE的面积与△ACE的面积的比值为.
故选D.
二、填空题
11.
【分析】本题考查了反比例函数的图象和性质,求出反比例函数解析式是解题关键.设该反比函数解析式为 ,根据当 时, ,可得该反比函数解析式为 ,再把代入,即可求出电流.
【详解】解:设该反比函数解析式为,由题意得:
,
解得:,
∴该反比函数解析式为,
当 时,.
故答案为:.
12.5
【详解】由题意可得三角形OAC的面积为3,可以求得AC=2,根据垂直平分线的性质,得到AB=OB,所以三角形ABC的周长=OC+AC=5
13.
【分析】本题主要考查了反比例函数的图象和性质,根据,得出,根据三角形面积公式,即可求出的面积;过点B作轴于点D,交于点E,根据,,得出,进而得出,根据梯形面积公式,列出方程,化简得,令,则,求出x的值,根据,得出,即,即可解答.
【详解】解:∵,
∴,
∴,
过点B作轴于点D,交于点E,
∵,
∴,
∴,
∵,,
∴,
∴,
∴,
整理得:,
令,
则,
解得:,,
∵,
∴,即,
∴,
故答案为: 2.
14.
【分析】根据函数图像的分布情况计算判断即可.
【详解】解:∵反比例函数与正比例函数的图像没有交点,经过第二、四象限,
∴经过第一、三象限,
∴,
解得 ,
故答案为:.
15.
【分析】有两函数的交点为,将代入一次函数与反比例函数解析式中得到与的值,再整体代入计算即可求出值.
【详解】解:把代入 ,
得
,
把代入,
得,
∴,
,
故答案为:.
16.4
【分析】本题考查求反比例函数值,关键是由已知函数解析式和自变量的值求相应的函数值.
【详解】解:当时,,
故答案为:4.
17.
【分析】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定满足此函数的解析式是解答此题的关键.
【详解】解:把点代入得:,
∴,
把点代入得:,
故答案为:.
18.3
【分析】设点,由矩形的面积可得;根据矩形的对角线互相平分可得,据此即可求解.
【详解】解:设点
∵矩形的面积为
∴
即:
∵对角线交于点D.
∴
∵反比例函数的图象经过点D
∴
故答案为:
19.
【分析】根据反比例函数的图像和性质作答即可.
【详解】解:∵,
∴反比例函数的图像在一、三象限,在每个象限,随增大而减小,
∵,
∴.
故答案为:.
20.
【分析】设点,过点D作x轴的垂线交于点G,过点A过x轴的平行线交于点H,过点A作轴于点N,根据先证明、可得,据此可得关于m的方程,求出m的值后,进一步即可求得答案.
【详解】解:设点,过点D作x轴的垂线交于点G,过点A过x轴的平行线交于点H,过点A作轴于点N,如图所示:
∵,
∴,
又,
∴,
∴,
同理,
∴,则点,,
,解得:,
故点,
则点,GE=,
OE=OG-GE=DH-GE=5-= ,
故答案为:.
三、解答题(60分)
21.解:(1)∵反比例函数(k为常数, k≠0)的图象经过点A(1,3),
∴,
解得k=3.
∴反比例函数的解析式为.
(2)设B(a,0),则OB=a.
∵△AOB的面积为6,
∴,
解得a=4.
∴B(4,0).
设直线AB的解析式为y=kx+b,
∵直线AB经过点A(1,3),点B(4,0),
∴
解得
∴直线AB的解析式y=-x+4.
22.解:(1)∵点A(1,2)在这个函数的图象上,
∴k﹣1=1×2,
解得k=3;
(2)∵在函数图象的每一支上,y随x的增大而增大,
∴k﹣1<0,
解得k<1;
(3)∵k=13,有k﹣1=12,
∴反比例函数的解析式为.
将点B的坐标代入,可知点B的坐标满足函数关系式,
∴点B在函数的图象上,
将点C的坐标代入,由5≠,可知点C的坐标不满足函数关系式,
∴点C不在函数的图象上.
23.解:(1)∵反比例函数y=的图象过点A(﹣2,1),B(1,n)
∴m=﹣2×1=﹣2,m=1×n
∴n=﹣2
∴B(1,﹣2)
∵一次函数y=kx+b的图象过点A,点B
∴
解得:k=﹣1,b=﹣1
∴直线解析式y=﹣x﹣1
(2)∵直线解析式y=﹣x﹣1与x轴交于点C
∴点C(﹣1,0)
∴S△AOB=×1×1+×1×2=
(3)由图象可得:x<﹣2或0<x<1
24.解:设.
∵点在其图象上,
∴所求函数表达式为;
由图象,知共需开挖水渠;
台挖掘机需要天;
.
故每天至少要完成.
25.(1)当时,由月利润与时间成反比例函数,设函数解析式为:,
由图可知:在函数图像上,
,
,
当时,
当时,设函数为,
由从6月初开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元,
,
由图可知,过点,
,
,
,
综上:,
(2)在函数中,令,得,
解得:,
答:到第13个月时,该化工厂月利润再次达到100万元.
(3)在函数中,
当时,,
∵,y随x的增大而减小,
∴当时,,
在函数中,
当时,得
解得:
∴且x为整数;
∴x可取3,4,5,6,7;共5个月.
答:该化工厂资金紧张期共有5个月
26.(1)解:因为爆炸前浓度呈直线型增加,
所以可设与的函数关系式为,
由图象知过点与,
,
解得,
,
此时自变量的取值范围是,
因为爆炸后浓度成反比例下降,所以可设与的函数关系式为,
由图象知过点,
,
,
,
此时自变量的取值范围是;
(2)解:当时,由得,,解得,
撤离的最长时间为(小时),
撤离的最小速度为
(3)解:当时,由得,,(小时),
27.(本题10分)如图,已知直线y=x与双曲线y=(k>0)交于A、B两点,且点A的横坐标为6
(1)求k的值;
(2)若双曲线y=(k>0)上一点C的纵坐标为9,求△AOC的面积;
(3)过原点O的另一条直线l交双曲线y=(k>0)于P、Q两点(P点在第一象限),若由点A、B、P、Q为顶点组成的四边形面积为96,求点P的坐标.
【答案】(1)18
(2)24
(3)P(18,1)或(2,9)
【分析】(1)先求得点的坐标,进而待定系数法求得反比例函数解析式;
(2)根据反比例函数的几何意义以及图形可得S△AOC=S△CON+S梯形AMNC-S△AOM=S梯形AMNC,据此求解即可
(3)由反比例函数的图象关于原点对称,可得由点A、B、P、Q为顶点组成的四边形是平行四边形,过A作AM⊥x轴于M,过P作PN⊥x轴于N,可得四边形APBQ的面积为96,根据S△AOP=S△AOM+S梯形AMNP-S△PON=S梯形AMNP,建立方程,解一元二次方程求解即可,然后根据P在第一象限,取值即可.
【详解】(1)解:在y=x中x=6时,y=3,即点A(6,3),
将点A(6,3)代入y=得:k=18;
(2)解:如图1,把y=9代入y=得,x=2,
如图所示,过点、分别作轴的垂线,垂足为、
∵点在双曲线上
∴当时,
∴点的坐标为, A(6,3),
∵点、在双曲线上
∴
S△AOC=S△CON+S梯形AMNC-S△AOM=S梯形AMNC=(9+3)(6-2)=24;
(3)解:如图2,∵反比例函数的图象关于原点对称,
∴由点A、B、P、Q为顶点组成的四边形是平行四边形,
∴PQ与AB交于O点,
过A作AM⊥x轴于M,过P作PN⊥x轴于N,
∵四边形APBQ的面积为96,
∴S△AOP=S四边形APBQ=24,
∵P在双曲线上,设P(x,),
∵S△AOP=S△AOM+S梯形AMNP-S△PON=S梯形AMNP,
∴(3+)|x-6|=24,
整理得x2-16x-36=0和x2+16x-36=0,
解得
∵P在第一象限,
解得x=2或18,
∴P(18,1)或(2,9);
一、单选题(30分)
1.若反比例函数的图象经过点,则m的值是( )
A.4 B. C.2 D.
2.下列函数:①,②,③,④,⑤,⑥,⑦,⑧.其中是的反比例函数的有( )
A.1个 B.2个 C.3个 D.4个
3.已知反比例函数的图象经过点,则此反比例函数的图象在( )
A.第一、二象限 B.第一、三象限 C.第二、四象限 D.第三、四象限
4.如图,的三个顶点分别为,,,若反比例函数的图像与有交点,则的取值范围是( ).
A. B. C. D.
5.如图,在平面直角坐标系中,反比例函数(k为常数)的图像与正比例函数的图像交于A、B两点,若,则k的值为( )
A.4 B. C. D.1
6.点,是反比例函数上关于原点对称的任意两点,平行于轴,交轴于点,平行于轴,交轴于点,设四边形的面积为,则( )
A. B. C. D.
7.一次函数和反比例函数的图象在同一坐标系中可能为( )
A. B. C. D.
8.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示,下列说法正确的是( ).
A.函数解析式为 B.蓄电池的电压是
C.当时, D.当时,
9.一次函数和反比例函数的图象如图所示,若,则x的取值范围是( )
A.或 B.或 C.或 D.
10.如图4,A、B是反比例函数的图象上的两点.AC、BD都垂直于x轴,垂足分别为C、D.AB的延长线交x轴于点E.若C、D的坐标分别为(1,0)、(4,0),则ΔBDE的面积与ΔACE的面积的比值是 ( )
A. B. C. D.
二、填空题(30分)
11.已知蓄电池的电压为定值,使用某蓄电池时,电流(单位:)与电阻(单位:)是反比例函数关系,它的图象如图所示,则当电阻为时,电流为 .
12.如图,已知点A在双曲线上,过点A作AC⊥x轴于点C,OC=3,线段OA的垂直平分线交OC于点B,则ABC的周长为 .
13.如图,点和在反比例函数的图象上,其中.过点A作轴于点C,若的面积为,则 .
14.反比例函数与正比例函数的图像没有交点,则k的取值范围为 .
15.设函数与的图象的交点坐标为,则的值为 .
16.在反比例函数中,当时函数的值为 .
17.若反比例函数的图像经过点和点,则
18.如图,在平面直角坐标系中,矩形的面积为,顶点A、C分别在x轴,y轴上,顶点B在第三象限,对角线交于点D.若反比例函数的图象经过点D,则k的值为 .
19.若点,,都在反比例函数(k为常数)的图像上,则,,的大小关系为 .(用“”连接)
20.如图,在平面直角坐标系中,正方形的顶点的坐标为,点在轴正半轴上,点在双曲线上,过点作轴交双曲线于点,则长为 .
三、解答题(60分)
21.如图,反比例函数(k为常数,且k≠0)经过点A(1,3).
(1)求反比例函数的解析式;
(2)在x轴正半轴上有一点B,若△AOB的面积为6,求直线AB的解析式.
22.已知反比例函数y=,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
23.已知如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A、B两点,A点坐标是(﹣2,1),B点坐标(1,n);
(1)求出k,b,m,n的值;
(2)求△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值的x的取值范围.
24.在李村河治理工程实验过程中,某工程队接受一项开挖水渠的工程,所需天数(天)与每天完成的工程量(天)的函数关系图象如图所示,是双曲线的一部分.
请根据题意,求与之间的函数表达式;
若该工程队有台挖掘机,每台挖掘机每天能够开挖水渠米,问该工程队需用多少天才能完成此项任务?
如果为了防汛工作的紧急需要,必须在一个月内(按天计算)完成任务,那么每天至少要完成多少米?
25.受新冠肺炎疫情的影响,某化工厂从2022年1月开始产量下降.借此机会,为了贯彻“发展循环经济,提高工厂效益”的绿色发展理念;管理人员对生产线进行为期5个月的升级改造,改造期间的月利润与时间成反比例函数;从6月初开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2022年1月为第1个月,第x(x为正整数)个月的利润为y万元,其图象如图所示,试解决下列问题:
(1)分别直接写出该化工厂对生产线进行升级改造前后,y与x的函数表达式,并写出自变量范围;
(2)到第几个月时,该化工厂月利润才能再次达到100万元?
(3)当月利润少于50万元时,为该化工厂的资金紧张期,问该化工厂资金紧张期共有几个月?
26.近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是.在一次矿难事件的调查中发现:从零时起,井内空气中的浓度达到,此后浓度呈直线型增加,在第7小时达到最高值,发生爆炸;爆炸后,空气中的浓度成反比例下降.如图,根据题中相关信息回答下列问题:
(1)求爆炸前后空气中浓度与时间的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的浓度达到时,井下的矿工接到自动报警信号,这时他们至少要以多少的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的浓度降到及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?
27.如图,已知直线y=x与双曲线y=(k>0)交于A、B两点,且点A的横坐标为6
(1)求k的值;
(2)若双曲线y=(k>0)上一点C的纵坐标为9,求△AOC的面积;
(3)过原点O的另一条直线l交双曲线y=(k>0)于P、Q两点(P点在第一象限),若由点A、B、P、Q为顶点组成的四边形面积为96,求点P的坐标.
答案
一、单选题
1.B
【分析】根据反比例函数图象上点的坐标特征得到,然后解关于m的方程即可.
【详解】解:∵反比例函数的图象经过点,
∴,
∴.
故选B.
2.C
【分析】根据反比例的三种形式判断即可.
【详解】解:反比例的三种形式分别为:,,.
①中的次数是,是一次函数,不是反比例函数;
②,③是反比例函数;
④中分母是,故不是反比例函数;
⑤是反比例函数;
⑥中没有,故不是反比例函数;
⑦分母是,故不是反比例函数;
⑧中的次数是,是一次函数,不是反比例函数.
故有三个是反比例函数.
故选C.
3.C
【分析】本题考查了反比例函数的图象分布,根据题意,得,选择即可,熟练掌握图象分布的条件是解题的关键.
【详解】∵反比例函数的图象经过点,
∴,
故图象分布在第二、四象限,
故选C.
4.B
【分析】根据题意,先求得反比例函数图像经过点C时的k值,再求解直线的解析式,然后求得直线与反比例函数图像有相切于一点的k值,进而可求解.
【详解】解:由反比例函数的图像与有交点知,
当反比例函数的图像经过点时,则有,
当反比例函数的图像经过点时,则有,
此时反比例函数为,则点也在此反比例函数图像上,
设直线的解析式为,
将、代入,得,
解得,
∴直线的解析式为,
联立方程组,整理得,
由得,此时直线与反比例函数的图像相切于一点,
故当时,反比例函数的图像与有交点,
故选:B.
5.D
【分析】根据反比例函数与正比例函数的图像关于原点对称,设,则,根据勾股定理求得的长度,根据,求得的值,进而即可求解.
【详解】解:∵反比例函数(k为常数)的图像与正比例函数的图像交于A、B两点,
∴设,则,,
则,
,
,
解得(负值舍去),
,
,
故选D.
6.C
【分析】根据过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积可知,,再根据反比例函数的对称性可知,为中点,则,,进而求出四边形的面积.
【详解】解:,是函数的图象上关于原点对称的任意两点,且平行于轴,平行于轴,
,
假设点坐标为,则点坐标为,
则,
,,
四边形面积.
故选:C
7.C
【分析】此题考查反比例函数和一次函数的图象共存问题;结合图象分别分析一次函数与反比例函数中,的符号,得出一致的符合题意,得出矛盾的不符合题意,从而可得答案.
【详解】解:A选项:由反比例函数的性质知k、b同号,由一次函数图象得,,得k、b异号.两者不一致,故A不符合题意;
B选项:由反比例函数的性质知k、b同号,由一次函数图象得,,两者不一致,故B不符合题意;
C选项:由反比例函数的性质知k、b异号,由一次函数图象得,,k、b异号,两者一致,故C符合题意;
D选项:由反比例函数的性质知k、b异号,由一次函数图象得,,k、b同号,两者不一致.故D不符合题意;
故选C
8.D
【分析】根据反比例函数图象,并结合物理学科中的电流等于电压除以电阻的知识点即可求解.
【详解】解:设,
∵图象过,
∴,
∵,
∴蓄电池的电压是,
∴选项A、B错误,不符合题意;
当时,,
∴选项C错误,不符合题意;
当时,,
由图象可知:当时,,
∴选项D正确,符合题意,
故选:D.
9.B
【分析】此题考查了根据反比例函数和一次函数图形,求出自变量取值范围,根据图象,找出使一次函数图象低于反比例函数图象时自变量的取值范围即可.
【详解】解:由图可知,当或时,,
故选:B.
10.D
【分析】根据函数解析式求得AC=2,BD=,再证明△BDE∽△ACE,根据相似三角形的性质即可求解.
【详解】解:∵C、D的坐标分别为(1,0),(4,0),
∴AC=2,BD=,
∵AC⊥CD,BD⊥CD,
∴∠ACD=∠BDE=90°,
∴,
∴△BDE∽△ACE,
∴△BDE的面积与△ACE的面积的比值为.
故选D.
二、填空题
11.
【分析】本题考查了反比例函数的图象和性质,求出反比例函数解析式是解题关键.设该反比函数解析式为 ,根据当 时, ,可得该反比函数解析式为 ,再把代入,即可求出电流.
【详解】解:设该反比函数解析式为,由题意得:
,
解得:,
∴该反比函数解析式为,
当 时,.
故答案为:.
12.5
【详解】由题意可得三角形OAC的面积为3,可以求得AC=2,根据垂直平分线的性质,得到AB=OB,所以三角形ABC的周长=OC+AC=5
13.
【分析】本题主要考查了反比例函数的图象和性质,根据,得出,根据三角形面积公式,即可求出的面积;过点B作轴于点D,交于点E,根据,,得出,进而得出,根据梯形面积公式,列出方程,化简得,令,则,求出x的值,根据,得出,即,即可解答.
【详解】解:∵,
∴,
∴,
过点B作轴于点D,交于点E,
∵,
∴,
∴,
∵,,
∴,
∴,
∴,
整理得:,
令,
则,
解得:,,
∵,
∴,即,
∴,
故答案为: 2.
14.
【分析】根据函数图像的分布情况计算判断即可.
【详解】解:∵反比例函数与正比例函数的图像没有交点,经过第二、四象限,
∴经过第一、三象限,
∴,
解得 ,
故答案为:.
15.
【分析】有两函数的交点为,将代入一次函数与反比例函数解析式中得到与的值,再整体代入计算即可求出值.
【详解】解:把代入 ,
得
,
把代入,
得,
∴,
,
故答案为:.
16.4
【分析】本题考查求反比例函数值,关键是由已知函数解析式和自变量的值求相应的函数值.
【详解】解:当时,,
故答案为:4.
17.
【分析】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定满足此函数的解析式是解答此题的关键.
【详解】解:把点代入得:,
∴,
把点代入得:,
故答案为:.
18.3
【分析】设点,由矩形的面积可得;根据矩形的对角线互相平分可得,据此即可求解.
【详解】解:设点
∵矩形的面积为
∴
即:
∵对角线交于点D.
∴
∵反比例函数的图象经过点D
∴
故答案为:
19.
【分析】根据反比例函数的图像和性质作答即可.
【详解】解:∵,
∴反比例函数的图像在一、三象限,在每个象限,随增大而减小,
∵,
∴.
故答案为:.
20.
【分析】设点,过点D作x轴的垂线交于点G,过点A过x轴的平行线交于点H,过点A作轴于点N,根据先证明、可得,据此可得关于m的方程,求出m的值后,进一步即可求得答案.
【详解】解:设点,过点D作x轴的垂线交于点G,过点A过x轴的平行线交于点H,过点A作轴于点N,如图所示:
∵,
∴,
又,
∴,
∴,
同理,
∴,则点,,
,解得:,
故点,
则点,GE=,
OE=OG-GE=DH-GE=5-= ,
故答案为:.
三、解答题(60分)
21.解:(1)∵反比例函数(k为常数, k≠0)的图象经过点A(1,3),
∴,
解得k=3.
∴反比例函数的解析式为.
(2)设B(a,0),则OB=a.
∵△AOB的面积为6,
∴,
解得a=4.
∴B(4,0).
设直线AB的解析式为y=kx+b,
∵直线AB经过点A(1,3),点B(4,0),
∴
解得
∴直线AB的解析式y=-x+4.
22.解:(1)∵点A(1,2)在这个函数的图象上,
∴k﹣1=1×2,
解得k=3;
(2)∵在函数图象的每一支上,y随x的增大而增大,
∴k﹣1<0,
解得k<1;
(3)∵k=13,有k﹣1=12,
∴反比例函数的解析式为.
将点B的坐标代入,可知点B的坐标满足函数关系式,
∴点B在函数的图象上,
将点C的坐标代入,由5≠,可知点C的坐标不满足函数关系式,
∴点C不在函数的图象上.
23.解:(1)∵反比例函数y=的图象过点A(﹣2,1),B(1,n)
∴m=﹣2×1=﹣2,m=1×n
∴n=﹣2
∴B(1,﹣2)
∵一次函数y=kx+b的图象过点A,点B
∴
解得:k=﹣1,b=﹣1
∴直线解析式y=﹣x﹣1
(2)∵直线解析式y=﹣x﹣1与x轴交于点C
∴点C(﹣1,0)
∴S△AOB=×1×1+×1×2=
(3)由图象可得:x<﹣2或0<x<1
24.解:设.
∵点在其图象上,
∴所求函数表达式为;
由图象,知共需开挖水渠;
台挖掘机需要天;
.
故每天至少要完成.
25.(1)当时,由月利润与时间成反比例函数,设函数解析式为:,
由图可知:在函数图像上,
,
,
当时,
当时,设函数为,
由从6月初开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元,
,
由图可知,过点,
,
,
,
综上:,
(2)在函数中,令,得,
解得:,
答:到第13个月时,该化工厂月利润再次达到100万元.
(3)在函数中,
当时,,
∵,y随x的增大而减小,
∴当时,,
在函数中,
当时,得
解得:
∴且x为整数;
∴x可取3,4,5,6,7;共5个月.
答:该化工厂资金紧张期共有5个月
26.(1)解:因为爆炸前浓度呈直线型增加,
所以可设与的函数关系式为,
由图象知过点与,
,
解得,
,
此时自变量的取值范围是,
因为爆炸后浓度成反比例下降,所以可设与的函数关系式为,
由图象知过点,
,
,
,
此时自变量的取值范围是;
(2)解:当时,由得,,解得,
撤离的最长时间为(小时),
撤离的最小速度为
(3)解:当时,由得,,(小时),
27.(本题10分)如图,已知直线y=x与双曲线y=(k>0)交于A、B两点,且点A的横坐标为6
(1)求k的值;
(2)若双曲线y=(k>0)上一点C的纵坐标为9,求△AOC的面积;
(3)过原点O的另一条直线l交双曲线y=(k>0)于P、Q两点(P点在第一象限),若由点A、B、P、Q为顶点组成的四边形面积为96,求点P的坐标.
【答案】(1)18
(2)24
(3)P(18,1)或(2,9)
【分析】(1)先求得点的坐标,进而待定系数法求得反比例函数解析式;
(2)根据反比例函数的几何意义以及图形可得S△AOC=S△CON+S梯形AMNC-S△AOM=S梯形AMNC,据此求解即可
(3)由反比例函数的图象关于原点对称,可得由点A、B、P、Q为顶点组成的四边形是平行四边形,过A作AM⊥x轴于M,过P作PN⊥x轴于N,可得四边形APBQ的面积为96,根据S△AOP=S△AOM+S梯形AMNP-S△PON=S梯形AMNP,建立方程,解一元二次方程求解即可,然后根据P在第一象限,取值即可.
【详解】(1)解:在y=x中x=6时,y=3,即点A(6,3),
将点A(6,3)代入y=得:k=18;
(2)解:如图1,把y=9代入y=得,x=2,
如图所示,过点、分别作轴的垂线,垂足为、
∵点在双曲线上
∴当时,
∴点的坐标为, A(6,3),
∵点、在双曲线上
∴
S△AOC=S△CON+S梯形AMNC-S△AOM=S梯形AMNC=(9+3)(6-2)=24;
(3)解:如图2,∵反比例函数的图象关于原点对称,
∴由点A、B、P、Q为顶点组成的四边形是平行四边形,
∴PQ与AB交于O点,
过A作AM⊥x轴于M,过P作PN⊥x轴于N,
∵四边形APBQ的面积为96,
∴S△AOP=S四边形APBQ=24,
∵P在双曲线上,设P(x,),
∵S△AOP=S△AOM+S梯形AMNP-S△PON=S梯形AMNP,
∴(3+)|x-6|=24,
整理得x2-16x-36=0和x2+16x-36=0,
解得
∵P在第一象限,
解得x=2或18,
∴P(18,1)或(2,9);
