人教版九年级数学下册 第二十七章 相似三角形 章节测试卷(含详解)
文档属性
| 名称 | 人教版九年级数学下册 第二十七章 相似三角形 章节测试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 861.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-04 19:13:31 | ||
图片预览

文档简介
第二十七章《相似三角形》章节测试卷
一、单选题(30分)
1.两个相似三角形的面积比为1︰3,则它们对应中线的比为( )
A.1︰3 B.1︰ C.1︰9 D.︰1
2.下列命题中:①任意两个等腰三角形都相似;②任意两个等边三角形都相似;③任意两个直角三角形都相似;④任意两个等腰直角三角形都相似;正确的是( )
A.①③ B.①④ C.②④ D.③④
3.下列各组的四条线段a,b,c,d是成比例线段的是( )
A. B.
C. D.
4.阳光下同一时刻,物高与影长成正比例,如果身高为1.5m的小丽,影长为2.5m,则此时影长为30m的旗杆的高为( )
A.20m B.18m C.16m D.15m
5.如图,已知,那么下列结论正确的是( ).
A. B. C. D.
6.有一个多边形的边长分别是、、、、,和它相似的一个多边形最长边为,那么这个多边形的周长是( )
A.12cm B.18cm C.32cm D.48cm
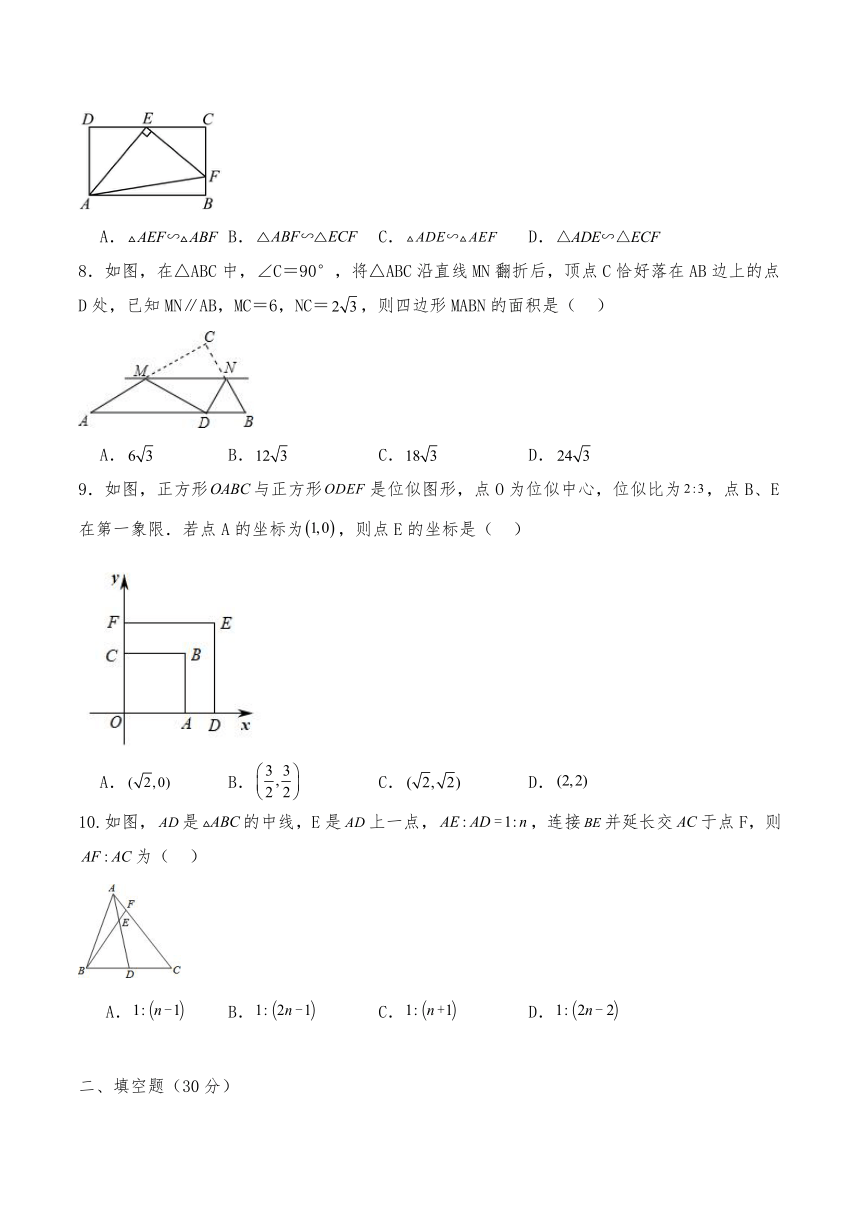
7.如图,在矩形中,E,F分别是,上的点.若,则一定有( )
A. B. C. D.
8.如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=,则四边形MABN的面积是( )
A. B. C. D.
9.如图,正方形与正方形是位似图形,点O为位似中心,位似比为,点B、E在第一象限.若点A的坐标为,则点E的坐标是( )
A. B. C. D.
10.如图,是的中线,E是上一点,,连接并延长交于点F,则为( )
A. B. C. D.
二、填空题(30分)
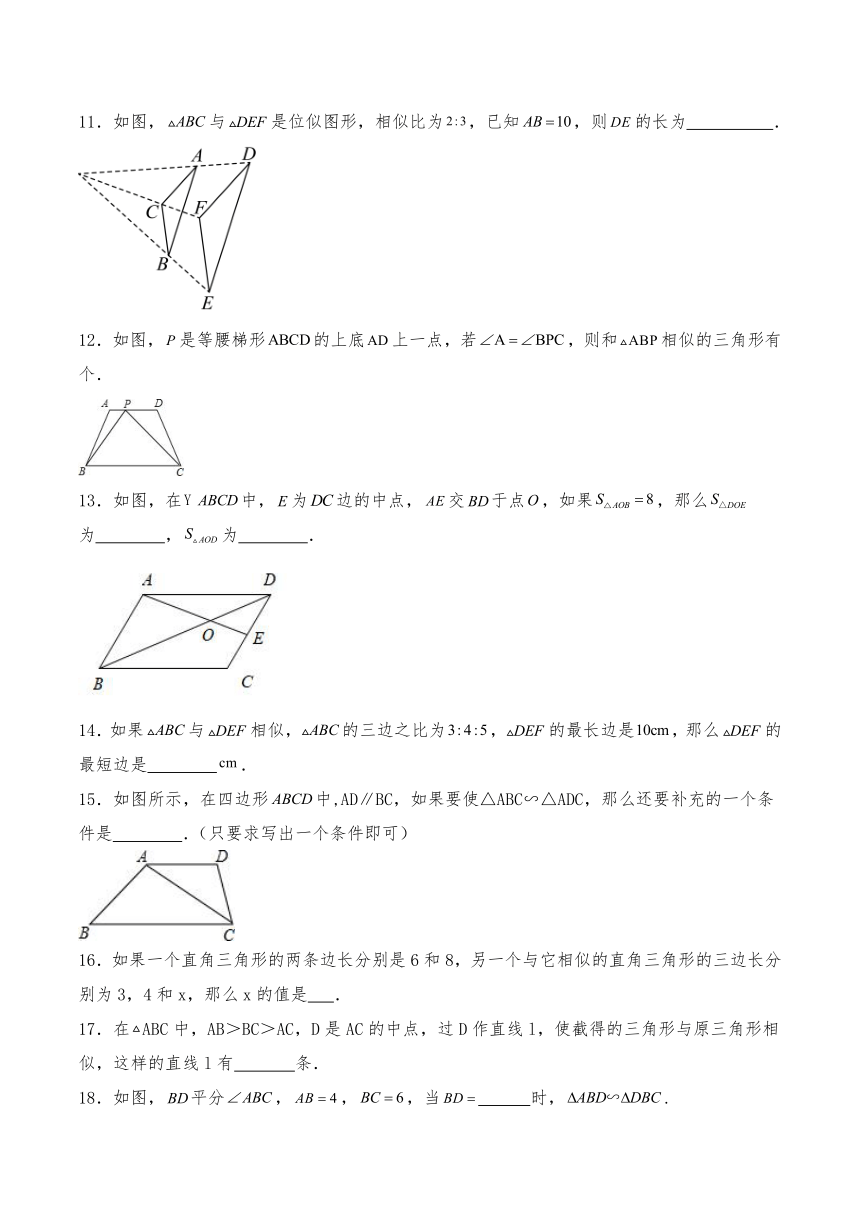
11.如图,与是位似图形,相似比为,已知,则的长为 .
12.如图,是等腰梯形的上底上一点,若,则和相似的三角形有 个.
13.如图,在中,为边的中点,交于点,如果,那么为 ,为 .
14.如果与相似,的三边之比为,的最长边是,那么的最短边是 .
15.如图所示,在四边形中,AD∥BC,如果要使△ABC∽△ADC,那么还要补充的一个条件是 .(只要求写出一个条件即可)
16.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形的三边长分别为3,4和x,那么x的值是 .
17.在ABC中,AB>BC>AC,D是AC的中点,过D作直线l,使截得的三角形与原三角形相似,这样的直线l有 条.
18.如图,平分,,,当 时,.
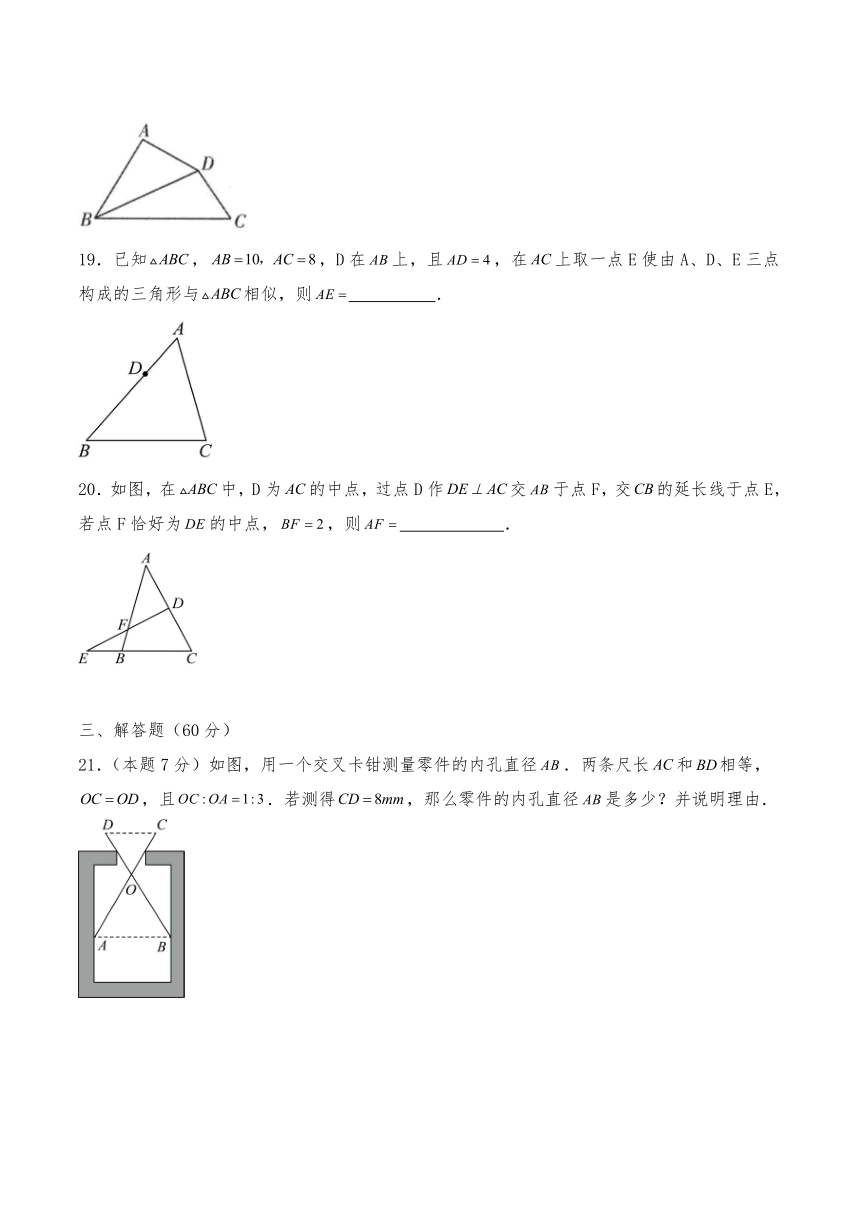
19.已知,,D在上,且,在上取一点E使由A、D、E三点构成的三角形与相似,则 .
20.如图,在中,D为的中点,过点D作交于点F,交的延长线于点E,若点F恰好为的中点,,则 .
三、解答题(60分)
21.(本题7分)如图,用一个交叉卡钳测量零件的内孔直径.两条尺长和相等,,且.若测得,那么零件的内孔直径是多少?并说明理由.
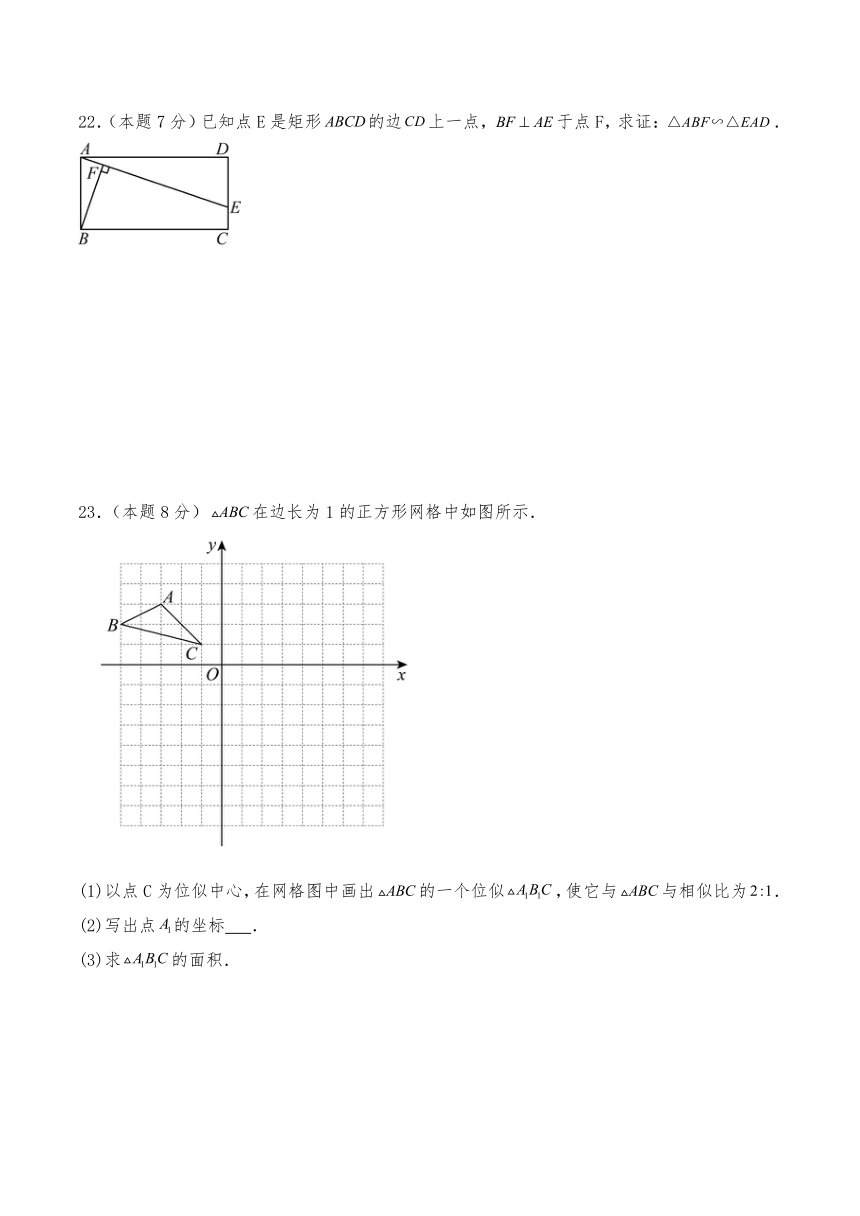
22.(本题7分)已知点E是矩形的边上一点,于点F,求证:.
23.(本题8分)在边长为1的正方形网格中如图所示.
(1)以点C为位似中心,在网格图中画出的一个位似,使它与与相似比为.
(2)写出点的坐标 .
(3)求的面积.
24.(本题8分)如图,河对岸有一路灯杆,在灯光下,小明在点D处测得自己的影长,沿方向到达点F处再测得自己的影长.如果小明的身高为,求路灯杆的高度.
25.(本题10分)如图,在四边形ABCD中,ADBC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.
(1)求证:ABE∽DBC;
(2)求线段AE的长.
26.(本题10分)如图,△ABC是等边三角形,⊙O过点B,C,且与BA,CA的延长线分别交于点D,E,弦DF∥AC,EF的延长线交BC的延长线于点G.
(1)求证:△BEF是等边三角形;
(2)若BA=4,CG=2,求BF的长.
27.(本题10分)如图,在平面直角坐标系中,A是抛物线上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
(1)当时,求S的值.
(2)求S关于的函数解析式.
(3)①若S=时,求的值;
②当m>2时,设,猜想k与m的数量关系并证明.
一、单选题
1.B
【分析】根据相似三角形的对应中线的比等于相似比解即可.
【详解】解:∵两个相似三角形的面积比为1:3,
∴它们的相似比为1:,
∴它们对应的中线的比为1:.
故选:B.
2.C
【分析】根据相似三角形的判定方法对各个选项进行分析,从而得到答案.
【详解】解:①不正确,因为没有说明角或边相等的条件,故不一定相似;
②正确,因为等边三个角都相等,故两三角形相似;
③不正确,只知道一个直角相等,不符合相似三角形判定的条件,故不一定相似;
④正确,因为其三对角均相等,符合相似三角形的判定条件,故相似;
所以②④正确,
故选:C.
3.D
【分析】根据比例线段的定义,让最小的和最大的相乘,另外两个相乘,看它们的积是否相等,对选项一一分析,即可得出答案.
【详解】解:A、,故此选项不符合题意;
B、,故此选项不符合题意;
C、,故此选项不符合题意;
D、,故此选项符合题意,
故选:D.
4.B
【分析】本题只要把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,求解即可得出旗杆的高.
【详解】解:根据题意,
即,
∴旗杆的高m,
故选:B.
5.D
【分析】根据平行线分线段成比例定理判断即可.
【详解】解:∵,
∴,
故选:D.
6.C
【分析】根据两多边形相似求出其相似比,再根据相似多边形周长的比等于相似比进行解答即可.
【详解】解:∵一个多边形的边长分别是4cm、5cm、6cm、4cm、5cm,和它相似的一个多边形最长边为8cm,
∴两个相似多边形的形似比为:,
设另一个多边形的周长为xcm,
∴ ,
解得x=32cm.
故选C.
7.D
【分析】根据矩形性质,得到,结合,得到,判定即可,熟练掌握三角形相似的判定定理是解题的关键.
【详解】∵矩形,
∴,
∵,
∴,
∴,
其余都不满足相似的条件,
故选D.
8.C
【详解】连接CD,交MN于E,
∵将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,
∴MN⊥CD,且CE=DE.∴CD=2CE.
∵MN∥AB,∴CD⊥AB.∴△CMN∽△CAB.
∴.
∵在△CMN中,∠C=90°,MC=6,NC= ,∴
∴.
∴.故选C.
9.B
【分析】由题意可得,又由点A的坐标为,即可求得的长,又由正方形的性质,即可求得E点的坐标.
【详解】解:∵正方形与正方形是位似图形,O为位似中心,相似比为,
∴,
∵点A的坐标为,
即,
∴,
∵四边形是正方形,
∴.
∴E点的坐标为:.
故选:B.
10.B
【分析】作交于点H,根据是的中线,可得,根据平行线分线段成比例可得,有已知条件可得,进而可得.
【详解】解:作交于点H,
∵是的中线,
,
,
,
,
,
,
∴,
,
.
故选:B.
二、填空题(30分)
11.
【分析】根据相似比,列出比例式即可求解.
【详解】解:∵与是位似图形,相似比为,
∴
∴,
∵,
∴,
故答案为:.
12.2
【分析】根据已知及相似三角形的判定方法即可得到答案.
【详解】∵AD∥BC,
∴∠APB=∠CBP,∠DPC=∠BCP,
∵∠A=∠BPC,
∴△APB∽△PBC,
∵ABCD为等腰梯形,
∴∠A=∠D=∠BPC,
∴△DPC∽△PCB,
∴△ABP∽△PCB∽△DPC,
∴有2个三角形与△ABP相似.
故答案为2.
13. 2 4
【分析】由AB∥CD,证得△AOB∽△EOD,又E为DC边的中点,AB=CD,故相似比为AB:ED=2:1,根据相似三角形的面积比等于相似比的平方,可求S△EOD.由OB:OD=2:1可求出S△AOD.
【详解】解:在中,∵AB∥CD,
∴△ABO∽△EDO,
∴AB:DE=OB:OD=2:1,
∴△ABO与△EDO的面积的比是4:1,△ABO与△ADO的面积的比是2:1.
∵S△AOB=8,
∴S△EOD=2,S△AOD=4.
故答案为:2,4.
14.6
【分析】根据相似三角形的性质可得出的三边之比也为.设的最短边是,则,解出x的值,即得出的最短边的长.
【详解】解:∵与相似,的三边之比为,
∴的三边之比也为.
设的最短边是,
∵的最长边是,
∴,
解得:,
∴的最短边是.
故答案为:6.
15.或或(答案不唯一)
【分析】先由AD∥BC,得到∠DAC=∠ACB,然后利用相似三角形的判定定理,做题即可.
【详解】解:∵AD∥BC,
∴∠DAC=∠ACB,
∴当∠B=∠DCA或∠BAC=∠D或
∴都可得相似.
故答案为:∠B=∠DCA或∠BAC=∠D或(答案不唯一).
16.解: 如果6和8都是直角边,那么斜边是10,
由对应边成比例可知与它相似的直角三角形的斜边长为x,则,
即x=5,
如果6是直角边,8是斜边,那么另一条边是,
则,
即,
故答案为:5或.
17.4
【详解】分析:根据相似三角形的判定,过点D作AB、AC的平行线与第三边相交可得三角形与原三角形相似,以D为顶点作与∠B相等的角,然后利用两角对应相等,也可以得到三角形与原三角形相似.
解:
如图,DE∥AB交BC于点E,△DEC∽△ABC,
DF∥BC交AB于点F,△AFD∽△ABC,
作∠CDG=∠B,又∵∠C=∠C,
∴△GDC∽△ABC,
作∠ADH=∠B,又∵∠A=∠A,
∴△ADH∽△ABC,
∴共可以作4条.
故填4.
18.
【分析】根据两边对应成比例,夹角相等,两三角形相似,列出比例式进行计算即可得解.
【详解】解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵△ABD∽△DBC,
∴,
∵AB=4,BC=6,
∴,
解得BD=
故答案为.
19.3.2或5
【分析】由A、D、E三点构成的三角形与相似,要分成两种情况来进行讨论,无论哪一种情况,将已知线段的长度代入后比例式后都能较容易的求出的值.
【详解】解:∵与相似,
∴或,
∵,
∴或,
解得:或.
故答案为:3.2或5.
20.
【分析】本题考查的是平行线分线段成比例,线段中点的含义,如图,过作,证明与,从而可得答案,熟记平行线分线段成比例是解本题的关键.
【详解】解:如图,过作,
∴,
∵为的中点,即,
∴,
∵,
∴,
∵D为的中点,即,
∴,
∴,
故答案为:
三、解答题
21.解:两条尺长和相等,,
,
,
,
,
,
,
,
.
22.证明:∵四边形为矩形,
∴,
∴,
∵于点,
∴,
∴,
∴.
23.(1)如图所示,即为所求;
(2)点的坐标 ,
故答案为:;
(3)的面积.
24.解:由题意得,,,
∴,
∴,
∴,
∴,即,
解得,
经检验,是原方程的解,
∴,
∴,
∴,
∴路灯杆的高度为.
25.(1)∵AB=AD=25,
∴∠ABD=∠ADB,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC,
∵AE⊥BD,
∴∠AEB=∠C=90°,
∴△ABE∽△DBC;
(2)∵AB=AD,AE⊥BD,
∴BE=DE,
∴BD=2BE,
∵△ABE∽△DBC,
∴,
∵AB=AD=25,BC=32,
∴,
∴BE=20,
∴AE==15.
26.(1)证明:∵△ABC是等边三角形,
∴∠BCA=∠BAC=60°,
∵DF∥AC,
∴∠D=∠BAC=60°,∠BEF=∠D=60°,
又∵∠BFE=∠BCA=60°,
∴△BEF是等边三角形.
(2)解:∵∠ABC=∠EBF=60°,
∴∠FBG=∠ABE,
又∠BFG=∠BAE=120°,
∴△BFG∽△BAE,
∴ ,
又BG=BC+CG=AB+CG=6,BE=BF,
∴BF2=AB BG=24,
可得BF=2(舍去负值).
27.(本题10分)如图,在平面直角坐标系中,A是抛物线上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
(1)当时,求S的值.
(2)求S关于的函数解析式.
(3)①若S=时,求的值;
②当m>2时,设,猜想k与m的数量关系并证明.
【答案】(1);(2);(3)①;②,证明见解析.
【详解】试题分析:(1)根据点在曲线上点的坐标与方程的关系,求出点A的坐标,根据△ABE∽△CBO求出CO的长,从而根据轴对称的性质求出DO的长,进而求出△BED的面积S.
(2)分和两种情况讨论.
(3)①连接AD,由△BED的面积为求出现,得到点A 的坐标,应用待定系数法,设
得到,从而.
②连接AD,应用待定系数法,设得到,从而得到,因此.
得到,从而
试题解析:(1)∵点A是抛物线上的一个动点,AE⊥y轴于点E,且,
∴点A的坐标为.∴当时,点A的坐标为.
∵点B的坐标为,∴BE=OE=1.
∵AE⊥y轴,∴AE∥x轴. ∴△ABE∽△CBO.∴,即,解得.
∵点D与点C关于y轴对称,∴.
∴.
(2)①当时,如图,
∵点D与点C关于y轴对称,∴△DBO≌△CBO.
∵△ABE∽△CBO,∴△ABE∽△DBO .∴.∴
∴.
②当时,如图,同①可得
综上所述,S关于的函数解析式.
(3)①如图,连接AD,
∵△BED的面积为,∴.∴点A 的坐标为.
设,∴.
∴.
∴.
②k与m的数量关系为,证明如下:
连接AD,则
∵,∴.
∴.
∵点A 的坐标为,∴.
一、单选题(30分)
1.两个相似三角形的面积比为1︰3,则它们对应中线的比为( )
A.1︰3 B.1︰ C.1︰9 D.︰1
2.下列命题中:①任意两个等腰三角形都相似;②任意两个等边三角形都相似;③任意两个直角三角形都相似;④任意两个等腰直角三角形都相似;正确的是( )
A.①③ B.①④ C.②④ D.③④
3.下列各组的四条线段a,b,c,d是成比例线段的是( )
A. B.
C. D.
4.阳光下同一时刻,物高与影长成正比例,如果身高为1.5m的小丽,影长为2.5m,则此时影长为30m的旗杆的高为( )
A.20m B.18m C.16m D.15m
5.如图,已知,那么下列结论正确的是( ).
A. B. C. D.
6.有一个多边形的边长分别是、、、、,和它相似的一个多边形最长边为,那么这个多边形的周长是( )
A.12cm B.18cm C.32cm D.48cm
7.如图,在矩形中,E,F分别是,上的点.若,则一定有( )
A. B. C. D.
8.如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=,则四边形MABN的面积是( )
A. B. C. D.
9.如图,正方形与正方形是位似图形,点O为位似中心,位似比为,点B、E在第一象限.若点A的坐标为,则点E的坐标是( )
A. B. C. D.
10.如图,是的中线,E是上一点,,连接并延长交于点F,则为( )
A. B. C. D.
二、填空题(30分)
11.如图,与是位似图形,相似比为,已知,则的长为 .
12.如图,是等腰梯形的上底上一点,若,则和相似的三角形有 个.
13.如图,在中,为边的中点,交于点,如果,那么为 ,为 .
14.如果与相似,的三边之比为,的最长边是,那么的最短边是 .
15.如图所示,在四边形中,AD∥BC,如果要使△ABC∽△ADC,那么还要补充的一个条件是 .(只要求写出一个条件即可)
16.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形的三边长分别为3,4和x,那么x的值是 .
17.在ABC中,AB>BC>AC,D是AC的中点,过D作直线l,使截得的三角形与原三角形相似,这样的直线l有 条.
18.如图,平分,,,当 时,.
19.已知,,D在上,且,在上取一点E使由A、D、E三点构成的三角形与相似,则 .
20.如图,在中,D为的中点,过点D作交于点F,交的延长线于点E,若点F恰好为的中点,,则 .
三、解答题(60分)
21.(本题7分)如图,用一个交叉卡钳测量零件的内孔直径.两条尺长和相等,,且.若测得,那么零件的内孔直径是多少?并说明理由.
22.(本题7分)已知点E是矩形的边上一点,于点F,求证:.
23.(本题8分)在边长为1的正方形网格中如图所示.
(1)以点C为位似中心,在网格图中画出的一个位似,使它与与相似比为.
(2)写出点的坐标 .
(3)求的面积.
24.(本题8分)如图,河对岸有一路灯杆,在灯光下,小明在点D处测得自己的影长,沿方向到达点F处再测得自己的影长.如果小明的身高为,求路灯杆的高度.
25.(本题10分)如图,在四边形ABCD中,ADBC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.
(1)求证:ABE∽DBC;
(2)求线段AE的长.
26.(本题10分)如图,△ABC是等边三角形,⊙O过点B,C,且与BA,CA的延长线分别交于点D,E,弦DF∥AC,EF的延长线交BC的延长线于点G.
(1)求证:△BEF是等边三角形;
(2)若BA=4,CG=2,求BF的长.
27.(本题10分)如图,在平面直角坐标系中,A是抛物线上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
(1)当时,求S的值.
(2)求S关于的函数解析式.
(3)①若S=时,求的值;
②当m>2时,设,猜想k与m的数量关系并证明.
一、单选题
1.B
【分析】根据相似三角形的对应中线的比等于相似比解即可.
【详解】解:∵两个相似三角形的面积比为1:3,
∴它们的相似比为1:,
∴它们对应的中线的比为1:.
故选:B.
2.C
【分析】根据相似三角形的判定方法对各个选项进行分析,从而得到答案.
【详解】解:①不正确,因为没有说明角或边相等的条件,故不一定相似;
②正确,因为等边三个角都相等,故两三角形相似;
③不正确,只知道一个直角相等,不符合相似三角形判定的条件,故不一定相似;
④正确,因为其三对角均相等,符合相似三角形的判定条件,故相似;
所以②④正确,
故选:C.
3.D
【分析】根据比例线段的定义,让最小的和最大的相乘,另外两个相乘,看它们的积是否相等,对选项一一分析,即可得出答案.
【详解】解:A、,故此选项不符合题意;
B、,故此选项不符合题意;
C、,故此选项不符合题意;
D、,故此选项符合题意,
故选:D.
4.B
【分析】本题只要把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,求解即可得出旗杆的高.
【详解】解:根据题意,
即,
∴旗杆的高m,
故选:B.
5.D
【分析】根据平行线分线段成比例定理判断即可.
【详解】解:∵,
∴,
故选:D.
6.C
【分析】根据两多边形相似求出其相似比,再根据相似多边形周长的比等于相似比进行解答即可.
【详解】解:∵一个多边形的边长分别是4cm、5cm、6cm、4cm、5cm,和它相似的一个多边形最长边为8cm,
∴两个相似多边形的形似比为:,
设另一个多边形的周长为xcm,
∴ ,
解得x=32cm.
故选C.
7.D
【分析】根据矩形性质,得到,结合,得到,判定即可,熟练掌握三角形相似的判定定理是解题的关键.
【详解】∵矩形,
∴,
∵,
∴,
∴,
其余都不满足相似的条件,
故选D.
8.C
【详解】连接CD,交MN于E,
∵将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,
∴MN⊥CD,且CE=DE.∴CD=2CE.
∵MN∥AB,∴CD⊥AB.∴△CMN∽△CAB.
∴.
∵在△CMN中,∠C=90°,MC=6,NC= ,∴
∴.
∴.故选C.
9.B
【分析】由题意可得,又由点A的坐标为,即可求得的长,又由正方形的性质,即可求得E点的坐标.
【详解】解:∵正方形与正方形是位似图形,O为位似中心,相似比为,
∴,
∵点A的坐标为,
即,
∴,
∵四边形是正方形,
∴.
∴E点的坐标为:.
故选:B.
10.B
【分析】作交于点H,根据是的中线,可得,根据平行线分线段成比例可得,有已知条件可得,进而可得.
【详解】解:作交于点H,
∵是的中线,
,
,
,
,
,
,
∴,
,
.
故选:B.
二、填空题(30分)
11.
【分析】根据相似比,列出比例式即可求解.
【详解】解:∵与是位似图形,相似比为,
∴
∴,
∵,
∴,
故答案为:.
12.2
【分析】根据已知及相似三角形的判定方法即可得到答案.
【详解】∵AD∥BC,
∴∠APB=∠CBP,∠DPC=∠BCP,
∵∠A=∠BPC,
∴△APB∽△PBC,
∵ABCD为等腰梯形,
∴∠A=∠D=∠BPC,
∴△DPC∽△PCB,
∴△ABP∽△PCB∽△DPC,
∴有2个三角形与△ABP相似.
故答案为2.
13. 2 4
【分析】由AB∥CD,证得△AOB∽△EOD,又E为DC边的中点,AB=CD,故相似比为AB:ED=2:1,根据相似三角形的面积比等于相似比的平方,可求S△EOD.由OB:OD=2:1可求出S△AOD.
【详解】解:在中,∵AB∥CD,
∴△ABO∽△EDO,
∴AB:DE=OB:OD=2:1,
∴△ABO与△EDO的面积的比是4:1,△ABO与△ADO的面积的比是2:1.
∵S△AOB=8,
∴S△EOD=2,S△AOD=4.
故答案为:2,4.
14.6
【分析】根据相似三角形的性质可得出的三边之比也为.设的最短边是,则,解出x的值,即得出的最短边的长.
【详解】解:∵与相似,的三边之比为,
∴的三边之比也为.
设的最短边是,
∵的最长边是,
∴,
解得:,
∴的最短边是.
故答案为:6.
15.或或(答案不唯一)
【分析】先由AD∥BC,得到∠DAC=∠ACB,然后利用相似三角形的判定定理,做题即可.
【详解】解:∵AD∥BC,
∴∠DAC=∠ACB,
∴当∠B=∠DCA或∠BAC=∠D或
∴都可得相似.
故答案为:∠B=∠DCA或∠BAC=∠D或(答案不唯一).
16.解: 如果6和8都是直角边,那么斜边是10,
由对应边成比例可知与它相似的直角三角形的斜边长为x,则,
即x=5,
如果6是直角边,8是斜边,那么另一条边是,
则,
即,
故答案为:5或.
17.4
【详解】分析:根据相似三角形的判定,过点D作AB、AC的平行线与第三边相交可得三角形与原三角形相似,以D为顶点作与∠B相等的角,然后利用两角对应相等,也可以得到三角形与原三角形相似.
解:
如图,DE∥AB交BC于点E,△DEC∽△ABC,
DF∥BC交AB于点F,△AFD∽△ABC,
作∠CDG=∠B,又∵∠C=∠C,
∴△GDC∽△ABC,
作∠ADH=∠B,又∵∠A=∠A,
∴△ADH∽△ABC,
∴共可以作4条.
故填4.
18.
【分析】根据两边对应成比例,夹角相等,两三角形相似,列出比例式进行计算即可得解.
【详解】解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵△ABD∽△DBC,
∴,
∵AB=4,BC=6,
∴,
解得BD=
故答案为.
19.3.2或5
【分析】由A、D、E三点构成的三角形与相似,要分成两种情况来进行讨论,无论哪一种情况,将已知线段的长度代入后比例式后都能较容易的求出的值.
【详解】解:∵与相似,
∴或,
∵,
∴或,
解得:或.
故答案为:3.2或5.
20.
【分析】本题考查的是平行线分线段成比例,线段中点的含义,如图,过作,证明与,从而可得答案,熟记平行线分线段成比例是解本题的关键.
【详解】解:如图,过作,
∴,
∵为的中点,即,
∴,
∵,
∴,
∵D为的中点,即,
∴,
∴,
故答案为:
三、解答题
21.解:两条尺长和相等,,
,
,
,
,
,
,
,
.
22.证明:∵四边形为矩形,
∴,
∴,
∵于点,
∴,
∴,
∴.
23.(1)如图所示,即为所求;
(2)点的坐标 ,
故答案为:;
(3)的面积.
24.解:由题意得,,,
∴,
∴,
∴,
∴,即,
解得,
经检验,是原方程的解,
∴,
∴,
∴,
∴路灯杆的高度为.
25.(1)∵AB=AD=25,
∴∠ABD=∠ADB,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC,
∵AE⊥BD,
∴∠AEB=∠C=90°,
∴△ABE∽△DBC;
(2)∵AB=AD,AE⊥BD,
∴BE=DE,
∴BD=2BE,
∵△ABE∽△DBC,
∴,
∵AB=AD=25,BC=32,
∴,
∴BE=20,
∴AE==15.
26.(1)证明:∵△ABC是等边三角形,
∴∠BCA=∠BAC=60°,
∵DF∥AC,
∴∠D=∠BAC=60°,∠BEF=∠D=60°,
又∵∠BFE=∠BCA=60°,
∴△BEF是等边三角形.
(2)解:∵∠ABC=∠EBF=60°,
∴∠FBG=∠ABE,
又∠BFG=∠BAE=120°,
∴△BFG∽△BAE,
∴ ,
又BG=BC+CG=AB+CG=6,BE=BF,
∴BF2=AB BG=24,
可得BF=2(舍去负值).
27.(本题10分)如图,在平面直角坐标系中,A是抛物线上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
(1)当时,求S的值.
(2)求S关于的函数解析式.
(3)①若S=时,求的值;
②当m>2时,设,猜想k与m的数量关系并证明.
【答案】(1);(2);(3)①;②,证明见解析.
【详解】试题分析:(1)根据点在曲线上点的坐标与方程的关系,求出点A的坐标,根据△ABE∽△CBO求出CO的长,从而根据轴对称的性质求出DO的长,进而求出△BED的面积S.
(2)分和两种情况讨论.
(3)①连接AD,由△BED的面积为求出现,得到点A 的坐标,应用待定系数法,设
得到,从而.
②连接AD,应用待定系数法,设得到,从而得到,因此.
得到,从而
试题解析:(1)∵点A是抛物线上的一个动点,AE⊥y轴于点E,且,
∴点A的坐标为.∴当时,点A的坐标为.
∵点B的坐标为,∴BE=OE=1.
∵AE⊥y轴,∴AE∥x轴. ∴△ABE∽△CBO.∴,即,解得.
∵点D与点C关于y轴对称,∴.
∴.
(2)①当时,如图,
∵点D与点C关于y轴对称,∴△DBO≌△CBO.
∵△ABE∽△CBO,∴△ABE∽△DBO .∴.∴
∴.
②当时,如图,同①可得
综上所述,S关于的函数解析式.
(3)①如图,连接AD,
∵△BED的面积为,∴.∴点A 的坐标为.
设,∴.
∴.
∴.
②k与m的数量关系为,证明如下:
连接AD,则
∵,∴.
∴.
∵点A 的坐标为,∴.
