第十九章 一次函数 单元练习卷(含答案)人教版数学八年级下册
文档属性
| 名称 | 第十九章 一次函数 单元练习卷(含答案)人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 250.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-04 20:00:36 | ||
图片预览




文档简介
第十九章 一次函数
一、选择题
下列函数关系式:① ;② ;③ ;④ .其中一次函数的个数是
A. 个 B. 个 C. 个 D. 个
正比例函数的图象经过点 ,则这个图象必经过点
A. B. C. D.
直线 向下平移 个单位长度后得到的直线是
A. B.
C. D.
一次函数 的图象经过点 ,且 的值随 的值增大而增大,则点 的坐标可能为
A. B. C. D.
直线 与直线 的交点在第四象限,则 的取值范围是
A. B. C. D.
一次函数 的图象 如图所示,将直线 向下平移若干个单位后得直线 , 的函数表达式为 .下列说法中错误的是
A. B.
C. D.当 时,
已知A,B两地相距 ,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车,图中 , 分别表示甲、乙离开A地的路程 (单位:)与时间 (单位:)的函数关系的图象,设在这个过程中,甲、乙两人相距 (单位:),则 关于 的函数图象是
A. B.
C. D.
如图,甲、丙两地相距 ,一列快车从甲地驶往丙地,途中经过乙地;一列慢车从乙地驶往丙地,两车同时出发,同向而行,折线 表示两车之间的距离 与慢车行驶的时间 之间的函数关系.根据图中提供的信息,下列说法不正确的是
A.甲、乙两地之间的距离为
B.点 表示 时,快车追上慢车
C.快车速度是慢车速度的 倍
D.快车到达丙地时,慢车距丙地还有
二、填空题
请写出一个与 轴交于点 的一次函数的表达式 .
若函数 , 随 的增大而增大,则 满足的条件为 .
已知点 , 在直线 上,且直线经过第一、二、四象限,当 时, 与 的大小关系为 .
函数 和 的图象相交于点 ,则不等式 的解集 .
已知直线 与 轴交于点 ,直线 经过点 , 与 在 点相交所形成的夹角为 (如图所示),则直线 的函数表达式为 .
如图,已知 ,,,当 时, .
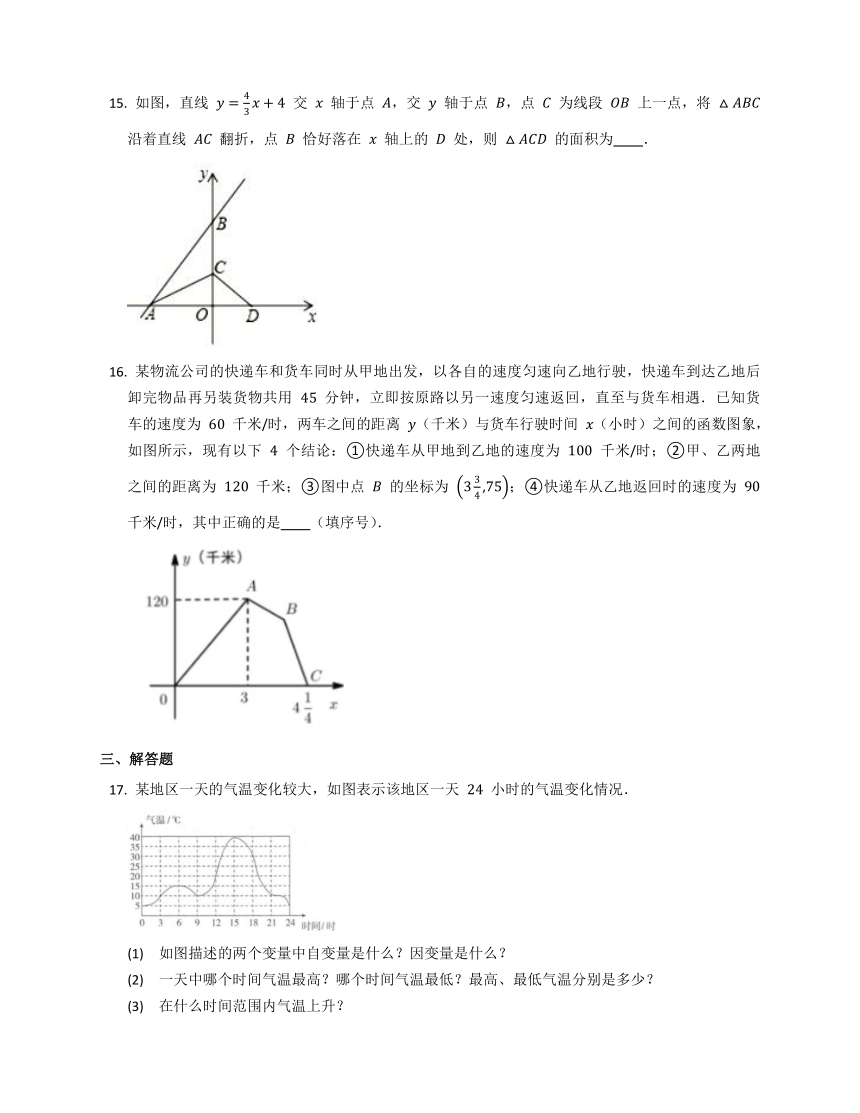
如图,直线 交 轴于点 ,交 轴于点 ,点 为线段 上一点,将 沿着直线 翻折,点 恰好落在 轴上的 处,则 的面积为 .
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用 分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为 千米/时,两车之间的距离 (千米)与货车行驶时间 (小时)之间的函数图象,如图所示,现有以下 个结论:①快递车从甲地到乙地的速度为 千米/时;②甲、乙两地之间的距离为 千米;③图中点 的坐标为 ;④快递车从乙地返回时的速度为 千米/时,其中正确的是 (填序号).
三、解答题
某地区一天的气温变化较大,如图表示该地区一天 小时的气温变化情况.
(1) 如图描述的两个变量中自变量是什么?因变量是什么?
(2) 一天中哪个时间气温最高?哪个时间气温最低?最高、最低气温分别是多少?
(3) 在什么时间范围内气温上升?
(4) 该地区一天的温差是多少?
已知一次函数图象经过点 ,.
()求这个一次函数的解析式;
()求这个一次函数图象与两坐标轴所围成的图形面积.
如图,直线 与直线 相交于点 .
(1) 求 的值;
(2) 不解关于 , 的方程组 请你直接写出它的解;
(3) 直线 是否也经过点 ?请说明理由.
某公司经营某种农产品,零售一箱该农产品的利润是 元,批发一箱该农产品的利润是 元.
(1) 已知该公司某月卖出 箱这种农产品,共获利润 元,问,该公司当月零售、批发这种农产品的箱数分别是多少?
(2) 经营性质规定,该公司零售的数量不能多于总数量的 .现该公司要经营 箱这种农产品,问:应如何规划零售和批发的数量,才能使总利润最大?最大总利润是多少元?
如图,在平面直角坐标系中,矩形 的边 位于 轴上,,,矩形的宽 为 .已知直线 .
(1) 证明:直线 始终经过一个定点,并写出该定点坐标;
(2) 当直线 与矩形 有交点时,求 的取值范围;
(3) 当直线 与折线 (不含点 )相交时,记交点为 ,设 的面积为 ,试求 与 的函数解析式.
如图,在平面直角坐标系中,过点 的直线 与直线 相交于点 ,动点 在线段 和射线 上运动.
(1) 求直线 的函数解析式;
(2) 求 的面积;
(3) 是否存在点 ,使 的面积与 的面积相等?若存在,求出此时点 的坐标;若不存在,请说明理由.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为 (小时),两车之间相距的路程为 (千米),图中的折线表示 与 之间的函数关系.
根据图象进行以下探究:
(1) 【信息读取】
()甲、乙两地之间相距的路程为 千米;
()请解释图中点 的实际意义;
(2) 【图象理解】
()求慢车和快车的速度;
()求线段 所表示的 与 之间的函数解析式,并写出自变量 的取值范围:
(3) 【问题解决】
()如果第二列快车也从甲地出发驶往乙地,速度与第一列快车相同,在第一列快车与慢车相遇 分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
答案
一、选择题
1. B
2. C
3. C
4. C
5. C
6. B
7. B
8. D
二、填空题
9.
10.
11.
12.
13.
14. 或
15.
16. ①③④
三、解答题
17.
(1) 由图象可知,时间是自变量,气温是因变量.
(2) 一天中 时和 时的气温最低,是 ; 时气温最高,是 .
(3) 在 时和 时,气温上升.
(4) 该地区一天的温差是 .
18. ()设一次函数的解析式为 ,
一次函数图象经过点 ,,
解得:
这个一次函数的解析式为 .
()设一次函数图象与 轴交于点 ,
令 ,
则 ,.
.
,
.
19.
(1) 在直线 上,
.
(2) 方程组的解是
(3) 直线 也经过点 .理由略.
20.
(1) 设该公司当月零售这种农产品 箱,则批发这种农产品 箱,
根据题意,得解得则 (箱).
答:该公司当月零售这种农产品 箱,批发这种农产品 箱.
(2) 设该公司当月零售这种农产品 箱,则批发这种农产品 箱,
根据题意,得解得设该公司获得的利润为 元,
根据题意,得 ,即 .
,
随着 的增大而增大,
当 时, 取最大值,
此时 ,
.
答:该公司零售、批发这种农产品的箱数分别是 箱, 箱时,才能使总利润最大,最大总利润为 元.
21.
(1) 不论 取何值,当 时, 恒成立,
该直线始终经过定点 .
(2) 当直线经过点 时,把 代入 得 ,解得 ;
当直线经过点 时,把 代入 得 ,解得 .
的取值范围是 .
(3) ,当直线经过点 时,
把点 的坐标 代入 得 ,解得 ,
当 时,点 在 上,则 ;
当 时,点 在 上,在 中,令 ,则 ,
,
.
综上所述,.
22.
(1) 设直线 的函数解析式是 .
根据题意,得 解得
直线 的函数解析式是 .
(2) ,当 时,,
点 的坐标为 ,
,
的面积 .
(3) 存在点 ,使 的面积与 的面积相等.
理由如下:
设直线 的函数解析式是 ,则 ,解得 .
直线 的函数解析式是 .
点 ,
,
,
的面积与 的面积相等,
点 到 轴的距离等于点 的纵坐标 ,
点 的横坐标为 或 .
当点 的横坐标为 ,即 时,
若点 在线段 上,则 ,
点 的坐标是 ;
若点 在射线 上,则 ,
点 的坐标是 .
当点 的横坐标为 ,即 时,
点 在射线 上,,
则点 的坐标是 .
综上所述,点 的坐标为 , 或 .
23.
(1) ();
()图中点 的实际意义是:当慢车行驶 小时时,慢车和快车相遇.
(2) ()由图象可知,慢车 小时行驶的路程为 千米,
所以慢车的速度为 (千米/小时);
当慢车行驶 小时时,慢车和快车相遇,两车行驶的路程之和为 千米,
所以慢车和快车行驶的速度之和为 (千米/小时),
所以快车的速度为 千米/小时.
()根据题意,快车行驶 千米到达乙地,
所以快车行驶 (小时)到达乙地,
此时两车之间的距离为 (千米),
所以点 的坐标为 .
设线段 所表示的 与 之间的函数关系式为 .
因为 , 在函数图象上,
所以 解得
所以线段 所表示的 与 之间的函数关系式为 ,定义域为 .
(3) ()慢车与第一列快车相遇 分钟后与第二列快车相遇,此时,慢车的行驶时间是 小时.
把 代入 ,得 .
此时,慢车与第一列快车之间的距离等于两列快车之间的距离是 千米,
所以两列快车出发的间隔时间是 (小时),即第二列快车比第一列快车晚出发 小时.
一、选择题
下列函数关系式:① ;② ;③ ;④ .其中一次函数的个数是
A. 个 B. 个 C. 个 D. 个
正比例函数的图象经过点 ,则这个图象必经过点
A. B. C. D.
直线 向下平移 个单位长度后得到的直线是
A. B.
C. D.
一次函数 的图象经过点 ,且 的值随 的值增大而增大,则点 的坐标可能为
A. B. C. D.
直线 与直线 的交点在第四象限,则 的取值范围是
A. B. C. D.
一次函数 的图象 如图所示,将直线 向下平移若干个单位后得直线 , 的函数表达式为 .下列说法中错误的是
A. B.
C. D.当 时,
已知A,B两地相距 ,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车,图中 , 分别表示甲、乙离开A地的路程 (单位:)与时间 (单位:)的函数关系的图象,设在这个过程中,甲、乙两人相距 (单位:),则 关于 的函数图象是
A. B.
C. D.
如图,甲、丙两地相距 ,一列快车从甲地驶往丙地,途中经过乙地;一列慢车从乙地驶往丙地,两车同时出发,同向而行,折线 表示两车之间的距离 与慢车行驶的时间 之间的函数关系.根据图中提供的信息,下列说法不正确的是
A.甲、乙两地之间的距离为
B.点 表示 时,快车追上慢车
C.快车速度是慢车速度的 倍
D.快车到达丙地时,慢车距丙地还有
二、填空题
请写出一个与 轴交于点 的一次函数的表达式 .
若函数 , 随 的增大而增大,则 满足的条件为 .
已知点 , 在直线 上,且直线经过第一、二、四象限,当 时, 与 的大小关系为 .
函数 和 的图象相交于点 ,则不等式 的解集 .
已知直线 与 轴交于点 ,直线 经过点 , 与 在 点相交所形成的夹角为 (如图所示),则直线 的函数表达式为 .
如图,已知 ,,,当 时, .
如图,直线 交 轴于点 ,交 轴于点 ,点 为线段 上一点,将 沿着直线 翻折,点 恰好落在 轴上的 处,则 的面积为 .
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用 分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为 千米/时,两车之间的距离 (千米)与货车行驶时间 (小时)之间的函数图象,如图所示,现有以下 个结论:①快递车从甲地到乙地的速度为 千米/时;②甲、乙两地之间的距离为 千米;③图中点 的坐标为 ;④快递车从乙地返回时的速度为 千米/时,其中正确的是 (填序号).
三、解答题
某地区一天的气温变化较大,如图表示该地区一天 小时的气温变化情况.
(1) 如图描述的两个变量中自变量是什么?因变量是什么?
(2) 一天中哪个时间气温最高?哪个时间气温最低?最高、最低气温分别是多少?
(3) 在什么时间范围内气温上升?
(4) 该地区一天的温差是多少?
已知一次函数图象经过点 ,.
()求这个一次函数的解析式;
()求这个一次函数图象与两坐标轴所围成的图形面积.
如图,直线 与直线 相交于点 .
(1) 求 的值;
(2) 不解关于 , 的方程组 请你直接写出它的解;
(3) 直线 是否也经过点 ?请说明理由.
某公司经营某种农产品,零售一箱该农产品的利润是 元,批发一箱该农产品的利润是 元.
(1) 已知该公司某月卖出 箱这种农产品,共获利润 元,问,该公司当月零售、批发这种农产品的箱数分别是多少?
(2) 经营性质规定,该公司零售的数量不能多于总数量的 .现该公司要经营 箱这种农产品,问:应如何规划零售和批发的数量,才能使总利润最大?最大总利润是多少元?
如图,在平面直角坐标系中,矩形 的边 位于 轴上,,,矩形的宽 为 .已知直线 .
(1) 证明:直线 始终经过一个定点,并写出该定点坐标;
(2) 当直线 与矩形 有交点时,求 的取值范围;
(3) 当直线 与折线 (不含点 )相交时,记交点为 ,设 的面积为 ,试求 与 的函数解析式.
如图,在平面直角坐标系中,过点 的直线 与直线 相交于点 ,动点 在线段 和射线 上运动.
(1) 求直线 的函数解析式;
(2) 求 的面积;
(3) 是否存在点 ,使 的面积与 的面积相等?若存在,求出此时点 的坐标;若不存在,请说明理由.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为 (小时),两车之间相距的路程为 (千米),图中的折线表示 与 之间的函数关系.
根据图象进行以下探究:
(1) 【信息读取】
()甲、乙两地之间相距的路程为 千米;
()请解释图中点 的实际意义;
(2) 【图象理解】
()求慢车和快车的速度;
()求线段 所表示的 与 之间的函数解析式,并写出自变量 的取值范围:
(3) 【问题解决】
()如果第二列快车也从甲地出发驶往乙地,速度与第一列快车相同,在第一列快车与慢车相遇 分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
答案
一、选择题
1. B
2. C
3. C
4. C
5. C
6. B
7. B
8. D
二、填空题
9.
10.
11.
12.
13.
14. 或
15.
16. ①③④
三、解答题
17.
(1) 由图象可知,时间是自变量,气温是因变量.
(2) 一天中 时和 时的气温最低,是 ; 时气温最高,是 .
(3) 在 时和 时,气温上升.
(4) 该地区一天的温差是 .
18. ()设一次函数的解析式为 ,
一次函数图象经过点 ,,
解得:
这个一次函数的解析式为 .
()设一次函数图象与 轴交于点 ,
令 ,
则 ,.
.
,
.
19.
(1) 在直线 上,
.
(2) 方程组的解是
(3) 直线 也经过点 .理由略.
20.
(1) 设该公司当月零售这种农产品 箱,则批发这种农产品 箱,
根据题意,得解得则 (箱).
答:该公司当月零售这种农产品 箱,批发这种农产品 箱.
(2) 设该公司当月零售这种农产品 箱,则批发这种农产品 箱,
根据题意,得解得设该公司获得的利润为 元,
根据题意,得 ,即 .
,
随着 的增大而增大,
当 时, 取最大值,
此时 ,
.
答:该公司零售、批发这种农产品的箱数分别是 箱, 箱时,才能使总利润最大,最大总利润为 元.
21.
(1) 不论 取何值,当 时, 恒成立,
该直线始终经过定点 .
(2) 当直线经过点 时,把 代入 得 ,解得 ;
当直线经过点 时,把 代入 得 ,解得 .
的取值范围是 .
(3) ,当直线经过点 时,
把点 的坐标 代入 得 ,解得 ,
当 时,点 在 上,则 ;
当 时,点 在 上,在 中,令 ,则 ,
,
.
综上所述,.
22.
(1) 设直线 的函数解析式是 .
根据题意,得 解得
直线 的函数解析式是 .
(2) ,当 时,,
点 的坐标为 ,
,
的面积 .
(3) 存在点 ,使 的面积与 的面积相等.
理由如下:
设直线 的函数解析式是 ,则 ,解得 .
直线 的函数解析式是 .
点 ,
,
,
的面积与 的面积相等,
点 到 轴的距离等于点 的纵坐标 ,
点 的横坐标为 或 .
当点 的横坐标为 ,即 时,
若点 在线段 上,则 ,
点 的坐标是 ;
若点 在射线 上,则 ,
点 的坐标是 .
当点 的横坐标为 ,即 时,
点 在射线 上,,
则点 的坐标是 .
综上所述,点 的坐标为 , 或 .
23.
(1) ();
()图中点 的实际意义是:当慢车行驶 小时时,慢车和快车相遇.
(2) ()由图象可知,慢车 小时行驶的路程为 千米,
所以慢车的速度为 (千米/小时);
当慢车行驶 小时时,慢车和快车相遇,两车行驶的路程之和为 千米,
所以慢车和快车行驶的速度之和为 (千米/小时),
所以快车的速度为 千米/小时.
()根据题意,快车行驶 千米到达乙地,
所以快车行驶 (小时)到达乙地,
此时两车之间的距离为 (千米),
所以点 的坐标为 .
设线段 所表示的 与 之间的函数关系式为 .
因为 , 在函数图象上,
所以 解得
所以线段 所表示的 与 之间的函数关系式为 ,定义域为 .
(3) ()慢车与第一列快车相遇 分钟后与第二列快车相遇,此时,慢车的行驶时间是 小时.
把 代入 ,得 .
此时,慢车与第一列快车之间的距离等于两列快车之间的距离是 千米,
所以两列快车出发的间隔时间是 (小时),即第二列快车比第一列快车晚出发 小时.
