22.1.4二次函数y=ax2+bx+c的图象和性质 课件(共22张PPT) 人教版数学九年级上册
文档属性
| 名称 | 22.1.4二次函数y=ax2+bx+c的图象和性质 课件(共22张PPT) 人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-04 20:08:43 | ||
图片预览







文档简介
(共22张PPT)
人教版九年级数学
22.1.4二次函数y=ax2+bx+c的图象和性质
第二十二章 二次函数
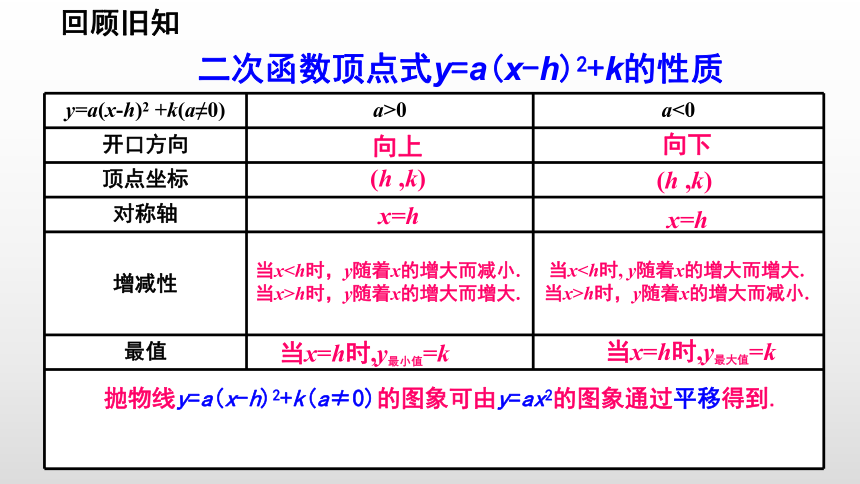
y=a(x-h)2 +k(a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增减性
最值
向上
向下
(h ,k)
(h ,k)
x=h
x=h
当x当x>h时,y随着x的增大而增大.
当x当x>h时,y随着x的增大而减小.
当x=h时,y最小值=k
当x=h时,y最大值=k
抛物线y=a(x-h)2+k(a≠0)的图象可由y=ax2的图象通过平移得到.
回顾旧知
二次函数顶点式y=a(x-h)2+k的性质
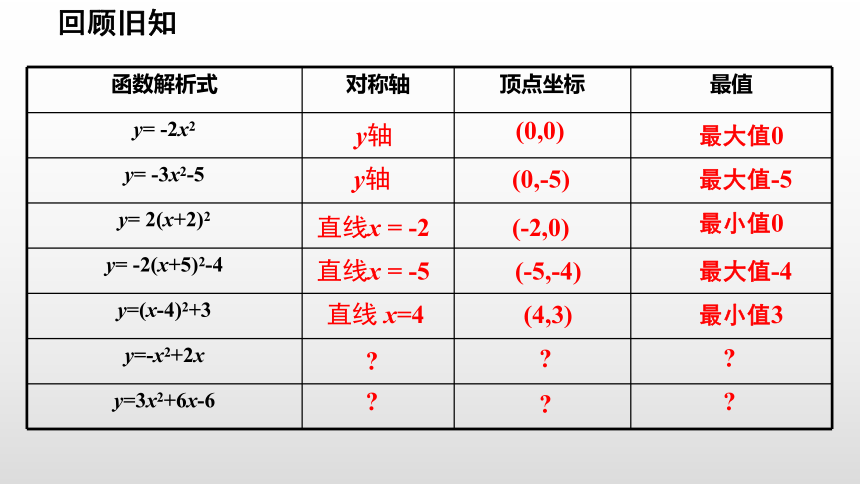
函数解析式 对称轴 顶点坐标 最值
y= -2x2
y= -3x2-5
y= 2(x+2)2
y= -2(x+5)2-4
y=(x-4)2+3
y=-x2+2x
y=3x2+6x-6
(0,0)
y轴
最大值0
(0,-5)
y轴
最大值-5
(-2,0)
直线x = -2
最小值0
(-5,-4)
直线x = -5
最大值-4
(4,3)
直线 x=4
最小值3
回顾旧知
画出二次函数y=ax2+bx+c的图象
我们已经知道y=a(x-h)2+k的图象和性质,能否利用这些知识来讨论 的图象和性质?
【思考1】怎样将 化成y=a(x-h)2+k的形式?
探究新知
知识点 1
配方可得
想一想:配方的方法及步骤是什么?
探究新知
怎样将 化成y=a(x-h)2+k的形式?
探究新知
配方
你知道是怎样配方的吗?
【提示】配方后的表达式通常称为配方式或顶点式.
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方式;
(3)“化”:化成顶点式.
【思考2】你能说出 的对称轴及顶点坐标吗?
答:对称轴是直线x=6,顶点坐标是(6,3).
【思考3】二次函数 可以看作是由 怎样平移得到的?
答:平移方法1:
先向上平移3个单位,再向右平移6个单位得到的;
平移方法2:
先向右平移6个单位,再向上平移3个单位得到的.
探究新知
【思考4】如何画二次函数 的图象?
…
…
…
…
9
8
7
6
5
4
3
x
1.利用图形的对称性列表
7.5
5
3.5
3
3.5
5
7.5
5
10
x
y
5
10
2.然后描点画图,得到图象如右图.
O
描点法:列表,描点,连线
探究新知
【思考5】结合二次函数 的图象,说出其性质.
5
10
x
y
5
10
当x<6时,y随x的增大而减小;
当x>6时,y随x的增大而增大.
O
探究新知
开口方向:
对称轴:
顶点:
向上
直线 x=6
(6,3)
x=6
最值:
当x=6时,y最小值=3
求二次函数y=2x2-8x+7图象的对称轴和顶点坐标.
因此,二次函数y=2x2-8x+7图象的对称轴是直线x=2,顶点坐标为(2,-1).
解:
应用新知:
例1
二次函数y=ax2+bx+c 的图象与性质
探究新知
知识点 2
我们如何用配方法将一般式y=ax2+bx+c(a≠0)
化成顶点式y=a(x-h)2+k?
探究新知
y=ax +bx+c
即y=ax2+bx+c
根据上面的关系你能发现二次函数y=ax2+bx+c的图象和性质吗?
y=ax2+bx+c
二次函数的顶点式
对称轴为 .
二次函数的一般表达式
因此,抛物线的对称轴是 ,顶点是 .
探究新知
y
O
x
(a>0)
y
O
x
(a<0)
二次函数y=ax2+bx+c的图象:
增减性?
最小值
最大值
探究新知
课堂小结
指出二次函数y=ax2+bx+c的有关性质
例2 二次函数y=x2+2x﹣3的开口方向、顶点坐标分别是( )
A.开口向上,顶点坐标为(﹣1,﹣4)
B.开口向下,顶点坐标为(1,4)
C.开口向上,顶点坐标为(1,4)
D.开口向下,顶点坐标为(﹣1,﹣4)
解析 ∵二次函数y=x2+2x﹣3的二次项系数为a=1>0,
∴函数图象开口向上,
∵y=x +2x﹣3=(x+1)2﹣4,
∴顶点坐标为(﹣1,﹣4).
方法点拨:把函数的一般式化为顶点式,再由顶点式确定开口方向、对称轴、顶点及其他性质.也可以用顶点坐标公式来确定.
A
应用新知:
函数解析式 对称轴 顶点坐标 最值
y= -2x2 y轴 (0,0) 最大值0
y= -3x2-5 y轴 (0,-5) 最大值-5
y= 2(x+2)2 直线x = -2 (-2,0) 最小值0
y= -2(x+5)2-4 直线x = -5 (-5,-4) 最大值-4
y=(x-4)2+3 直线 x=4 (4,3) 最小值3
y=-x2+2x
y=3x2+6x-6
应用新知
x=1
(1,1)
最大值1
x=-1
(1,-9)
最小值-9
顶点坐标 对称轴 最 值
y=-x2+2x
y=-2x2-1
y=9x2+6x-5
(1,1)
直线x=1
最大值1
(0,-1)
y轴(或直线x=0)
最大值-1
最小值-6
( ,-6)
直线x=
填一填.
巩固练习
应用新知:
1.通过这一节课的学习,你有哪些收获?
2.对这些内容你有什么体会?请与你的同伴交流.
课堂小结:
顶点:
对称轴:
y=ax2+bx+c(a ≠0)
(一般式)
配方法
公式法
(顶点式)
课堂总结
1.知识:
2.方法:1) 复习引入—类比猜想—探索—验证—归纳;
2) 特殊— 一般— 特殊.
3.思想:类比、转化、数形结合和归纳等数学思想.
已知二次函数y=-x2+2bx+c,当x>1时,y的值随x
值的增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1 C.b≥1 D.b≤1
D
拓展提升:
人教版九年级数学
22.1.4二次函数y=ax2+bx+c的图象和性质
第二十二章 二次函数
y=a(x-h)2 +k(a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增减性
最值
向上
向下
(h ,k)
(h ,k)
x=h
x=h
当x
当x
当x=h时,y最小值=k
当x=h时,y最大值=k
抛物线y=a(x-h)2+k(a≠0)的图象可由y=ax2的图象通过平移得到.
回顾旧知
二次函数顶点式y=a(x-h)2+k的性质
函数解析式 对称轴 顶点坐标 最值
y= -2x2
y= -3x2-5
y= 2(x+2)2
y= -2(x+5)2-4
y=(x-4)2+3
y=-x2+2x
y=3x2+6x-6
(0,0)
y轴
最大值0
(0,-5)
y轴
最大值-5
(-2,0)
直线x = -2
最小值0
(-5,-4)
直线x = -5
最大值-4
(4,3)
直线 x=4
最小值3
回顾旧知
画出二次函数y=ax2+bx+c的图象
我们已经知道y=a(x-h)2+k的图象和性质,能否利用这些知识来讨论 的图象和性质?
【思考1】怎样将 化成y=a(x-h)2+k的形式?
探究新知
知识点 1
配方可得
想一想:配方的方法及步骤是什么?
探究新知
怎样将 化成y=a(x-h)2+k的形式?
探究新知
配方
你知道是怎样配方的吗?
【提示】配方后的表达式通常称为配方式或顶点式.
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方式;
(3)“化”:化成顶点式.
【思考2】你能说出 的对称轴及顶点坐标吗?
答:对称轴是直线x=6,顶点坐标是(6,3).
【思考3】二次函数 可以看作是由 怎样平移得到的?
答:平移方法1:
先向上平移3个单位,再向右平移6个单位得到的;
平移方法2:
先向右平移6个单位,再向上平移3个单位得到的.
探究新知
【思考4】如何画二次函数 的图象?
…
…
…
…
9
8
7
6
5
4
3
x
1.利用图形的对称性列表
7.5
5
3.5
3
3.5
5
7.5
5
10
x
y
5
10
2.然后描点画图,得到图象如右图.
O
描点法:列表,描点,连线
探究新知
【思考5】结合二次函数 的图象,说出其性质.
5
10
x
y
5
10
当x<6时,y随x的增大而减小;
当x>6时,y随x的增大而增大.
O
探究新知
开口方向:
对称轴:
顶点:
向上
直线 x=6
(6,3)
x=6
最值:
当x=6时,y最小值=3
求二次函数y=2x2-8x+7图象的对称轴和顶点坐标.
因此,二次函数y=2x2-8x+7图象的对称轴是直线x=2,顶点坐标为(2,-1).
解:
应用新知:
例1
二次函数y=ax2+bx+c 的图象与性质
探究新知
知识点 2
我们如何用配方法将一般式y=ax2+bx+c(a≠0)
化成顶点式y=a(x-h)2+k?
探究新知
y=ax +bx+c
即y=ax2+bx+c
根据上面的关系你能发现二次函数y=ax2+bx+c的图象和性质吗?
y=ax2+bx+c
二次函数的顶点式
对称轴为 .
二次函数的一般表达式
因此,抛物线的对称轴是 ,顶点是 .
探究新知
y
O
x
(a>0)
y
O
x
(a<0)
二次函数y=ax2+bx+c的图象:
增减性?
最小值
最大值
探究新知
课堂小结
指出二次函数y=ax2+bx+c的有关性质
例2 二次函数y=x2+2x﹣3的开口方向、顶点坐标分别是( )
A.开口向上,顶点坐标为(﹣1,﹣4)
B.开口向下,顶点坐标为(1,4)
C.开口向上,顶点坐标为(1,4)
D.开口向下,顶点坐标为(﹣1,﹣4)
解析 ∵二次函数y=x2+2x﹣3的二次项系数为a=1>0,
∴函数图象开口向上,
∵y=x +2x﹣3=(x+1)2﹣4,
∴顶点坐标为(﹣1,﹣4).
方法点拨:把函数的一般式化为顶点式,再由顶点式确定开口方向、对称轴、顶点及其他性质.也可以用顶点坐标公式来确定.
A
应用新知:
函数解析式 对称轴 顶点坐标 最值
y= -2x2 y轴 (0,0) 最大值0
y= -3x2-5 y轴 (0,-5) 最大值-5
y= 2(x+2)2 直线x = -2 (-2,0) 最小值0
y= -2(x+5)2-4 直线x = -5 (-5,-4) 最大值-4
y=(x-4)2+3 直线 x=4 (4,3) 最小值3
y=-x2+2x
y=3x2+6x-6
应用新知
x=1
(1,1)
最大值1
x=-1
(1,-9)
最小值-9
顶点坐标 对称轴 最 值
y=-x2+2x
y=-2x2-1
y=9x2+6x-5
(1,1)
直线x=1
最大值1
(0,-1)
y轴(或直线x=0)
最大值-1
最小值-6
( ,-6)
直线x=
填一填.
巩固练习
应用新知:
1.通过这一节课的学习,你有哪些收获?
2.对这些内容你有什么体会?请与你的同伴交流.
课堂小结:
顶点:
对称轴:
y=ax2+bx+c(a ≠0)
(一般式)
配方法
公式法
(顶点式)
课堂总结
1.知识:
2.方法:1) 复习引入—类比猜想—探索—验证—归纳;
2) 特殊— 一般— 特殊.
3.思想:类比、转化、数形结合和归纳等数学思想.
已知二次函数y=-x2+2bx+c,当x>1时,y的值随x
值的增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1 C.b≥1 D.b≤1
D
拓展提升:
同课章节目录
