第九章 概率初步 3 等可能事件的概率 第3课时 几何概率(1) 同步练习(含答案)
文档属性
| 名称 | 第九章 概率初步 3 等可能事件的概率 第3课时 几何概率(1) 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 491.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-04 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第九章 概率初步
3 等可能事件的概率
第3课时 几何概率(1)
基础闯关
知识点一:与面积有关的几何概率
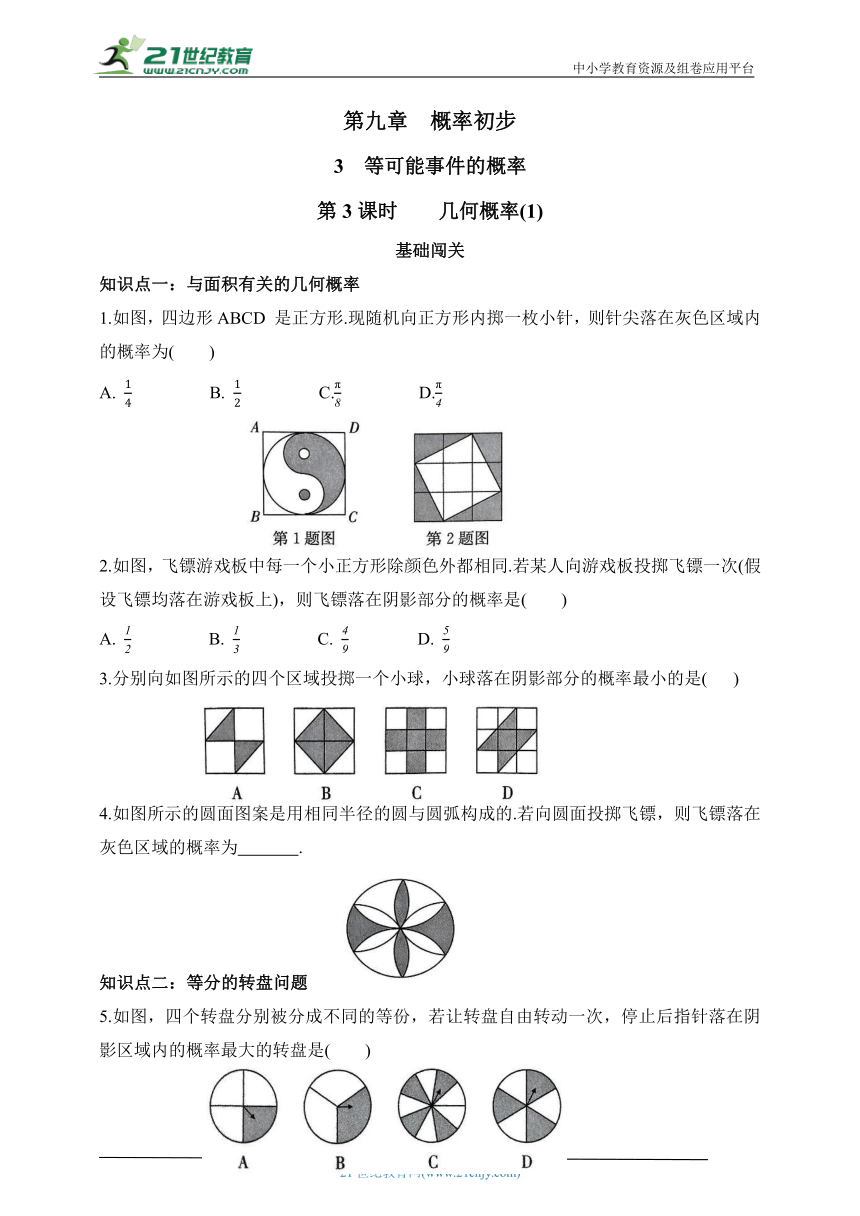
1.如图,四边形ABCD 是正方形.现随机向正方形内掷一枚小针,则针尖落在灰色区域内的概率为( )
A. B. C. D.
2.如图,飞镖游戏板中每一个小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖均落在游戏板上),则飞镖落在阴影部分的概率是( )
A. B. C. D.
3.分别向如图所示的四个区域投掷一个小球,小球落在阴影部分的概率最小的是( )
4.如图所示的圆面图案是用相同半径的圆与圆弧构成的.若向圆面投掷飞镖,则飞镖落在灰色区域的概率为 .
知识点二:等分的转盘问题
5.如图,四个转盘分别被分成不同的等份,若让转盘自由转动一次,停止后指针落在阴影区域内的概率最大的转盘是( )
6.二十四节气被列入联合国教科文组织人类非物质文化遗产代表作名录.太阳运行的轨道是一个圆形,古人将之称作“黄道”,并把黄道分为24份,每15度就是一个节气,统称“二十四节气”.这一时间认知体系被誉为“中国的第五大发明”.如图,指针落在惊蛰、春分、清明区域的概率是 .
能力提升
7.如图,在正方形ABCD 中,点M,N 是AB 的三等分点,分别以AM,AN 为边作正方形.正方形 ABCD 被分为如图所示的三个区域.小明同学在正方形 ABCD 内进行撒豆子试验,以下说法正确的是( )
A.豆子落在区域Ⅰ的概率最小 B.豆子落在区域Ⅱ的概率最小
C.豆子落在区域Ⅲ的概率最小 D.豆子落在区域Ⅰ,Ⅱ,Ⅲ的概率相同
8.如图,若随机向正方形内投一粒米(将米粒看成一个点),则米粒落在阴影部分的概率是 .(结果保留π)
9.[几何直观]如图,如果小球在用七巧板拼成的正方形中自由地滚动,并随机地停留在某区域,它最终停留在2号区域的概率为 .
10.[几何直观]如图,在6×5的长方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点,扇形OAB 的圆心及弧的两端均为格点.假设飞镖击中每一块小正方形是等可能的(击中扇形的边界或没有击中游戏板,则重投1次),任意投掷飞镖1 次,飞镖击中扇形OAB(阴影部分)的概率是 .
素养提升微专题
【用补形法或分割法求几何概率】
方法1:补形法
11.如图,一只蚂蚁在正方形ABCD 区域内爬行,点O 是对角线的交点,∠MON=90°,OM,ON 分别交线段AB,BC 于M,N两点,则蚂蚁停留在阴影区域的概率为 .
方法2:分割法
12.如图所示是一块三角形纸板,其中 AD =DF,BE=ED,EF=FC,一只蚂蚁在这块纸板上爬行,则蚂蚁停留在阴影部分的概率为 .
13.在如图所示的正三角形区域内投针(区域中每个小正三角形除颜色外完全相同),针随机落在某个小正三角形内(边线忽略不计).
(1)投针一次,针落在图中阴影区域的概率是多少
(2)要使针落在图中阴影区域和空白区域的概率均为 ,还要再涂灰几个小正三角形 请在图中画出.
培优创新
14.如图,在长方形OABC 中,顶点 A(8,0),C(0,6),直线y= kx-1分别交 BA,OA 于点D,E,且D为BA 的中点.
(1)求 k 的值及此时△EAD 的面积.
(2)现向长方形内随机投掷一枚飞镖,求飞镖落在△EAD内的概率.(若投在边框上则重投)
参考答案
第3课时 几何概率(1)
1. C [解析]设正方形 ABCD 的边长为2a,针尖落在灰色区域内的概率
2. C 3. A 4. 5. D 6. 7. A
8. 9. 10. 11. 12.
13.解:(1)因为阴影部分的面积与大三角形的面积的比值是 所以投针一次,针落在图中阴影区域的概率是 (2)还要再涂灰2个小正三角形,如图所示.
14.解:(1)∵在长方形OABC 中,顶点 A(8,0),C(0,6),∴B(8,6).
∵D为BA 的中点,∴D(8,3),AD=3.
把点D(8,3)代入,得
令y=0,得x=2,∴E(2,0),∴OE=2,AE=6,∴S△EAD= 6×3=9.
(2)由(1)得S长方形AOCB=6×8=48,∴飞镖落在△EAD内的概率是
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 概率初步
3 等可能事件的概率
第3课时 几何概率(1)
基础闯关
知识点一:与面积有关的几何概率
1.如图,四边形ABCD 是正方形.现随机向正方形内掷一枚小针,则针尖落在灰色区域内的概率为( )
A. B. C. D.
2.如图,飞镖游戏板中每一个小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖均落在游戏板上),则飞镖落在阴影部分的概率是( )
A. B. C. D.
3.分别向如图所示的四个区域投掷一个小球,小球落在阴影部分的概率最小的是( )
4.如图所示的圆面图案是用相同半径的圆与圆弧构成的.若向圆面投掷飞镖,则飞镖落在灰色区域的概率为 .
知识点二:等分的转盘问题
5.如图,四个转盘分别被分成不同的等份,若让转盘自由转动一次,停止后指针落在阴影区域内的概率最大的转盘是( )
6.二十四节气被列入联合国教科文组织人类非物质文化遗产代表作名录.太阳运行的轨道是一个圆形,古人将之称作“黄道”,并把黄道分为24份,每15度就是一个节气,统称“二十四节气”.这一时间认知体系被誉为“中国的第五大发明”.如图,指针落在惊蛰、春分、清明区域的概率是 .
能力提升
7.如图,在正方形ABCD 中,点M,N 是AB 的三等分点,分别以AM,AN 为边作正方形.正方形 ABCD 被分为如图所示的三个区域.小明同学在正方形 ABCD 内进行撒豆子试验,以下说法正确的是( )
A.豆子落在区域Ⅰ的概率最小 B.豆子落在区域Ⅱ的概率最小
C.豆子落在区域Ⅲ的概率最小 D.豆子落在区域Ⅰ,Ⅱ,Ⅲ的概率相同
8.如图,若随机向正方形内投一粒米(将米粒看成一个点),则米粒落在阴影部分的概率是 .(结果保留π)
9.[几何直观]如图,如果小球在用七巧板拼成的正方形中自由地滚动,并随机地停留在某区域,它最终停留在2号区域的概率为 .
10.[几何直观]如图,在6×5的长方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点,扇形OAB 的圆心及弧的两端均为格点.假设飞镖击中每一块小正方形是等可能的(击中扇形的边界或没有击中游戏板,则重投1次),任意投掷飞镖1 次,飞镖击中扇形OAB(阴影部分)的概率是 .
素养提升微专题
【用补形法或分割法求几何概率】
方法1:补形法
11.如图,一只蚂蚁在正方形ABCD 区域内爬行,点O 是对角线的交点,∠MON=90°,OM,ON 分别交线段AB,BC 于M,N两点,则蚂蚁停留在阴影区域的概率为 .
方法2:分割法
12.如图所示是一块三角形纸板,其中 AD =DF,BE=ED,EF=FC,一只蚂蚁在这块纸板上爬行,则蚂蚁停留在阴影部分的概率为 .
13.在如图所示的正三角形区域内投针(区域中每个小正三角形除颜色外完全相同),针随机落在某个小正三角形内(边线忽略不计).
(1)投针一次,针落在图中阴影区域的概率是多少
(2)要使针落在图中阴影区域和空白区域的概率均为 ,还要再涂灰几个小正三角形 请在图中画出.
培优创新
14.如图,在长方形OABC 中,顶点 A(8,0),C(0,6),直线y= kx-1分别交 BA,OA 于点D,E,且D为BA 的中点.
(1)求 k 的值及此时△EAD 的面积.
(2)现向长方形内随机投掷一枚飞镖,求飞镖落在△EAD内的概率.(若投在边框上则重投)
参考答案
第3课时 几何概率(1)
1. C [解析]设正方形 ABCD 的边长为2a,针尖落在灰色区域内的概率
2. C 3. A 4. 5. D 6. 7. A
8. 9. 10. 11. 12.
13.解:(1)因为阴影部分的面积与大三角形的面积的比值是 所以投针一次,针落在图中阴影区域的概率是 (2)还要再涂灰2个小正三角形,如图所示.
14.解:(1)∵在长方形OABC 中,顶点 A(8,0),C(0,6),∴B(8,6).
∵D为BA 的中点,∴D(8,3),AD=3.
把点D(8,3)代入,得
令y=0,得x=2,∴E(2,0),∴OE=2,AE=6,∴S△EAD= 6×3=9.
(2)由(1)得S长方形AOCB=6×8=48,∴飞镖落在△EAD内的概率是
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
