北师大版六下1.2《圆柱的表面积》(课件)
文档属性
| 名称 | 北师大版六下1.2《圆柱的表面积》(课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-05 11:50:31 | ||
图片预览







文档简介
(共34张PPT)
第三课时
圆柱的表面积
(北师大)六年级
下
01
学习目标
内容总览
02
新知导入
03
探究新知
04
课堂练习
05
课堂总结
06
分层作业
核心素养目标
使学生经历观察、操作、猜想、验证、类比和归纳等数学活动的过程,探索并掌握圆柱的体积公式,初步学会应用公式计算圆柱的体积,并能解决相关的实际问题
01
02
使学生在探索圆柱体积公式的过程中,进一步体会转化的思想方法,培养应用所学知识解决纹的能力,发展初步的推理能力和空间观念。
03
使学生在参与数学活动的过程中,进一步感受数学知识和方法的学习价值,获得些学习成功的体验,培养对数学学习的兴趣。
新知导入
什么是长方体或正方体表面积?
长方体或正方体6个面的总面积,叫作它的表面积。
学习任务一
圆柱表面积公式的推导
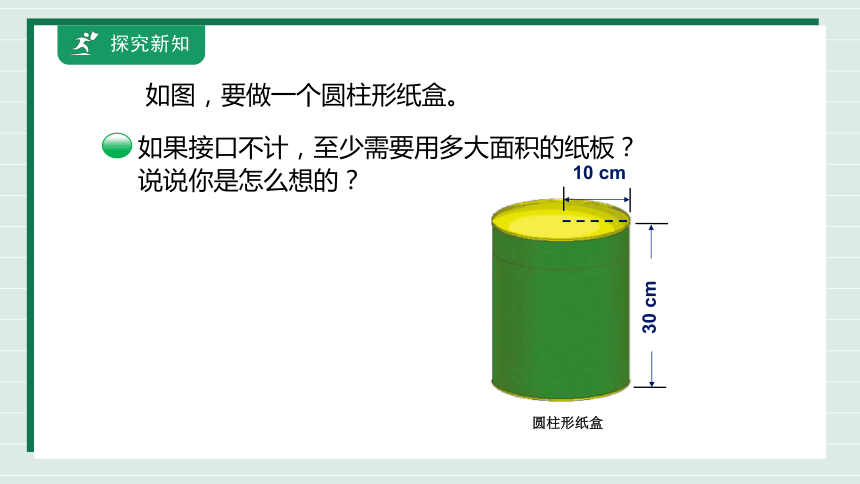
探究新知
如果接口不计,至少需要用多大面积的纸板?
说说你是怎么想的?
30 cm
10 cm
圆柱形纸盒
如图,要做一个圆柱形纸盒。
探究新知
如果接口不计,至少需要用多大面积的纸板?说说你是怎么想的?
实际上是求圆柱
的表面积。
2个底面面积(圆)
1个侧面面积
(曲面)
表面积
S=πr 2
+
圆柱的侧面
积怎样求呢?
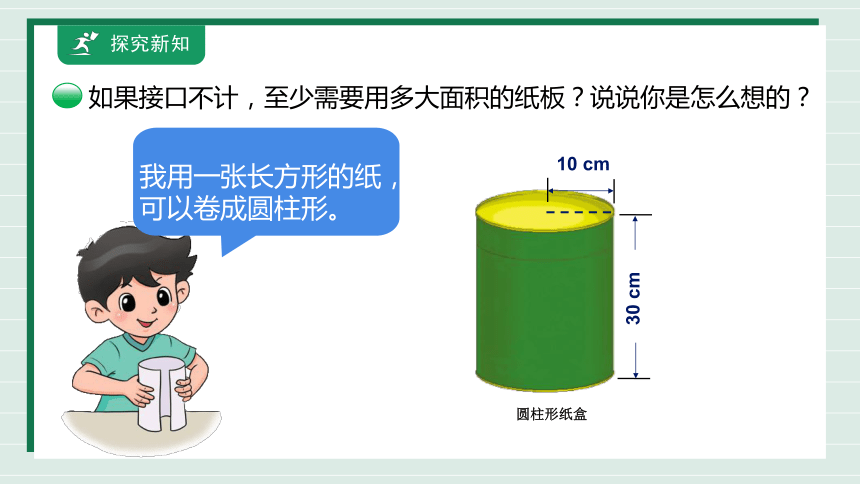
探究新知
我用一张长方形的纸, 可以卷成圆柱形。
30 cm
10 cm
圆柱形纸盒
如果接口不计,至少需要用多大面积的纸板?说说你是怎么想的?
探究新知
圆柱的侧面展开后是一个怎样的图形呢?你能想办法说明吗?
把圆柱的侧面剪开
看看,是一个什么
图形呢?
长方形
正方形
平行四边形
探究新知
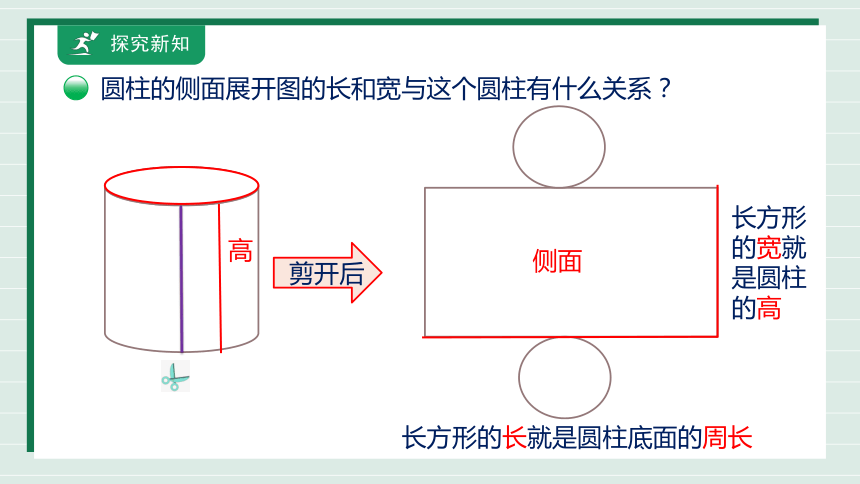
圆柱的侧面展开图的长和宽与这个圆柱有什么关系?
剪开后
侧面
高
长方形的宽就是圆柱的高
长方形的长就是圆柱底面的周长
探究新知
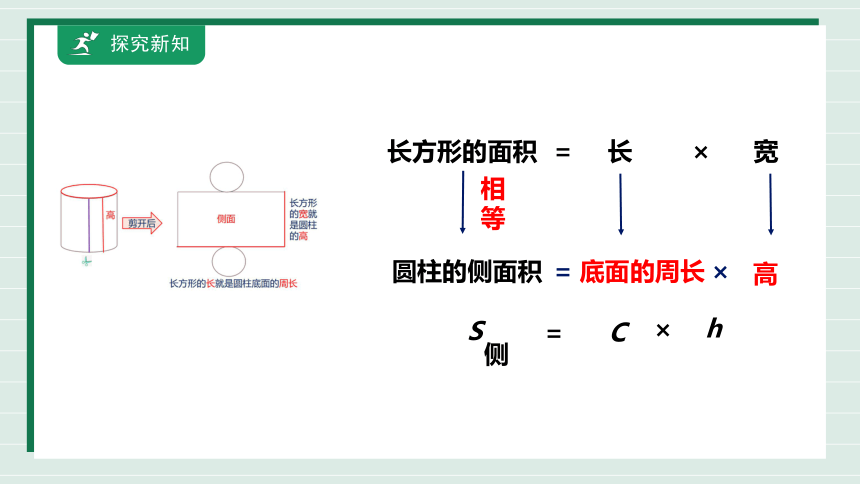
长方形的面积
=
长
×
宽
圆柱的侧面积
相等
底面的周长
高
=
×
S
侧
C
h
=
×
探究新知
圆柱的表面积 = 圆柱的侧面积 + 两个底面的面积
如果我们用
S底来表示圆柱的底面积,
S侧来表示圆柱的侧面积,
S表来表示圆柱的表面积,
那圆柱的表面积可以怎样计算呢?
S表= 2S底+ S侧
S表=2πr 2 +Ch
S表=2πr 2 +πdh
S表=2πr 2 +2πrh
或
或
探究新知
你能计算出“至少需要用多大面积的纸板吗”?
30 cm
10 cm
侧面积: _______________________
底面积:_______________________
表面积:_______________________
2×3.14×10×30=1884(cm2)
3.14×102×2=628(cm2)
1884+628=2512(cm2)
答:至少需要用2512平方厘米的纸板。
学习任务二
计算表面积时,需要计算哪些部分的面积?
探究新知
如图,做一个无盖的圆柱形铁皮水桶,底面直径为 4 dm,高为 5 dm,至少需要用多大面积的铁皮?
4 dm
5 dm
1.从题目中你能找到哪些数学信息?
2.水桶一共有几个面?
3.需要用多大面积的铁皮就是求水桶的什么面积?求圆柱哪几个面的面积?
4.列式解决问题。
5.解答这一道题需要注意什么?
探究新知
如图,做一个无盖的圆柱形铁皮水桶,底面直径为 4 dm,高为 5 dm,至少需要用多大面积的铁皮?
4 dm
5 dm
S表= S底+ S侧
S侧=
S底=
S表=
3.14×4×5=62.8(dm2)
3.14×(4÷2)2=12.56(dm2)
62.8+12.56=75.36(dm2)
答:至少需要75.36平方分米的铁皮。
探究新知
如图,把一个圆柱形薯片盒的商标纸展开,是一个长18.84cm,宽是10 cm的长方形。这个薯片盒的侧面积是多少?表面积呢?
S侧
S底
S底
10 cm
18.84 cm
C=18.84 cm
探究新知
如图,把一个圆柱形薯片盒的商标纸展开,是一个长18.84cm,宽是10 cm的长方形。这个薯片盒的侧面积是多少?表面积呢?
S侧=
18.84×10=188.4(cm2)
底面半径:
18.84÷3.14÷2=3(cm)
2S底=
3.14×32×2=56.52(cm2)
S表=
188.4+56.52=244.92(cm2)
答:这个薯片盒的侧面积是188.4cm2,表面积244.92cm2。
10 cm
18.84 cm
C=18.84 cm
探究新知
生活中,计算物体的表面积时,经常需要根据实际情况分析“需要计算哪些部分的面积”
玻璃杯的表面积
水桶的表面积
S表= S底+ S侧
1个侧面
1个底面
探究新知
柱子表面涂漆,求涂漆的面积。
求通风管所用材料的面积。
压路机前轮工作一圈的面积。
S表= S侧
1个侧面
课堂练习
1.填 空
(1)把圆柱的侧面沿着高剪开,可以得到一个( ),这个长方形的长等于圆柱的 ( ),宽等于圆柱的
( )
(2)当圆柱的底面周长和圆柱的高相等时,圆柱的侧面展开图是( )。
(3)圆柱有无数条( )。
(4)圆柱的侧面是一个( )。
长方形
底面周长
高
正方形
高
曲面
课堂练习
2.连一连,并在括号中填出相应的数。
( )
( )
( )
( )
9.42cm
8cm
3.14×3=9.42cm
21.98cm
4cm
3.14×7=21.98cm
8 cm
6 cm
课堂练习
3.求圆柱的表面积。
S表= 2S底+ S侧
S表= 2πr2 +πdh
= 3.14×(4÷2)2×2+4×3.14×6
= 100.48(cm2)
S表= 2S底+ S侧
S表= 2πr2 +2πrh
= 3.14×32×2+3×2×3.14×10
= 244.92(dm2)
课堂练习
4. 压路机前轮直径是1.6m,宽是2m,它转动一周,压路的面积是多少平方米?
3.14×1.6×2=10.048(m2)
答:压路的面积是10.048平方米。
前轮的侧面积
课堂练习
5. 一个圆柱形水池,水池内壁和底部都镶上瓷砖, 水池内部底面周长25.12m,池深1.2m,镶瓷砖的面积是多少平方米?
S表= S底+ S侧
S底=3.14×(25.12÷3.14÷2)2=50.24(m2)
S侧=25.12×1.2=30.144(m2)
S表=30.144+50.24=80.384(m2)
答:镶瓷砖的面积是80.384平方米。
课堂练习
6. 油桶的表面要刷上防锈油漆,每平方米需用防锈油漆0.2kg,刷一个油桶大约需要多少防锈油漆?(结果保留两位小数)
S表= 2S底+ S侧
S侧=3.14×0.6×1=1.884(m2)
2S底=3.14×(0.6÷2)2×2=0.5652(m2)
S表= 1.884+0.5652=2.4492(m2)
油漆:2.4492×0.2≈0.49(kg)
答:刷一个油桶大约需要0.49kg防锈油漆。
课堂总结
今天你有什么收获?
分层作业
【知识技能类作业】
1.判断。
(1)圆柱的侧面展开后一定是长方形。( )
(2)圆柱体的表面积=底面积×2+底面积×高( )
(3) 圆柱体的表面积一定比它的侧面积大。 ( )
(4)做一节圆柱形通风管要用多少铁皮,就是求它的侧面积。( )
x
x
√
x
分层作业
2.求下面圆柱的侧面积和表面积。
侧面积:3.14 x 4x2x8=200.96( cm2)
表面积:3.14 x 42x 2 +200.96= 301.44(cm2)
分层作业
3.填空。
(1)圆柱的底面半径扩大到原来的2倍,高不变,它的侧面积扩大到原来的( )倍。
A.2 B.4 C.6 D.8
(2)把一个底面积是 15.7cm 的圆柱切成3个同样大小的圆柱后,表面积增加了( )cm
A.15.7 B.31.4 C.47.1 D.62.8
A
D
分层作业
4.一个圆柱的侧面展开后是一个边长 31.4 dm 的正方形,这个圆柱的表面积是多少平方分米
31.4÷3.14÷2=5(dm)3.14x5 x2+31.4x31.4=1142.96(dm )
答:这个圆柱的表面积是 1142.96 dm 。
分层作业
5.如图,有一块长方形铁皮,涂色部分刚好能做成一个圆柱(接头处忽略不计),求这个圆柱的表面积。(提示:圆柱的底面周长等于长方形铁皮的长。)
底面半径:18.84÷3.14÷2=3(dm)
圆柱的高:10-3x2=4(dm)
圆柱的侧面积:18.84x 4=75.36( dm )
圆柱的表面积:75.36 +3.14 x 3 x 2=131.88( dm )答:这个圆柱的表面积是 131.88 dm 。
课堂练习
6. 做一做。
(1)找一个圆柱形物体,量出它的高和底面直径,计算出它的表面积。
(2)制作一个底面直径和高都是 10cm 的圆柱形纸盒。
【综合实践类作业】
https://www.21cnjy.com/help/help_extract.php
让备课更有效
www.21cnjy.com
Thanks!
第三课时
圆柱的表面积
(北师大)六年级
下
01
学习目标
内容总览
02
新知导入
03
探究新知
04
课堂练习
05
课堂总结
06
分层作业
核心素养目标
使学生经历观察、操作、猜想、验证、类比和归纳等数学活动的过程,探索并掌握圆柱的体积公式,初步学会应用公式计算圆柱的体积,并能解决相关的实际问题
01
02
使学生在探索圆柱体积公式的过程中,进一步体会转化的思想方法,培养应用所学知识解决纹的能力,发展初步的推理能力和空间观念。
03
使学生在参与数学活动的过程中,进一步感受数学知识和方法的学习价值,获得些学习成功的体验,培养对数学学习的兴趣。
新知导入
什么是长方体或正方体表面积?
长方体或正方体6个面的总面积,叫作它的表面积。
学习任务一
圆柱表面积公式的推导
探究新知
如果接口不计,至少需要用多大面积的纸板?
说说你是怎么想的?
30 cm
10 cm
圆柱形纸盒
如图,要做一个圆柱形纸盒。
探究新知
如果接口不计,至少需要用多大面积的纸板?说说你是怎么想的?
实际上是求圆柱
的表面积。
2个底面面积(圆)
1个侧面面积
(曲面)
表面积
S=πr 2
+
圆柱的侧面
积怎样求呢?
探究新知
我用一张长方形的纸, 可以卷成圆柱形。
30 cm
10 cm
圆柱形纸盒
如果接口不计,至少需要用多大面积的纸板?说说你是怎么想的?
探究新知
圆柱的侧面展开后是一个怎样的图形呢?你能想办法说明吗?
把圆柱的侧面剪开
看看,是一个什么
图形呢?
长方形
正方形
平行四边形
探究新知
圆柱的侧面展开图的长和宽与这个圆柱有什么关系?
剪开后
侧面
高
长方形的宽就是圆柱的高
长方形的长就是圆柱底面的周长
探究新知
长方形的面积
=
长
×
宽
圆柱的侧面积
相等
底面的周长
高
=
×
S
侧
C
h
=
×
探究新知
圆柱的表面积 = 圆柱的侧面积 + 两个底面的面积
如果我们用
S底来表示圆柱的底面积,
S侧来表示圆柱的侧面积,
S表来表示圆柱的表面积,
那圆柱的表面积可以怎样计算呢?
S表= 2S底+ S侧
S表=2πr 2 +Ch
S表=2πr 2 +πdh
S表=2πr 2 +2πrh
或
或
探究新知
你能计算出“至少需要用多大面积的纸板吗”?
30 cm
10 cm
侧面积: _______________________
底面积:_______________________
表面积:_______________________
2×3.14×10×30=1884(cm2)
3.14×102×2=628(cm2)
1884+628=2512(cm2)
答:至少需要用2512平方厘米的纸板。
学习任务二
计算表面积时,需要计算哪些部分的面积?
探究新知
如图,做一个无盖的圆柱形铁皮水桶,底面直径为 4 dm,高为 5 dm,至少需要用多大面积的铁皮?
4 dm
5 dm
1.从题目中你能找到哪些数学信息?
2.水桶一共有几个面?
3.需要用多大面积的铁皮就是求水桶的什么面积?求圆柱哪几个面的面积?
4.列式解决问题。
5.解答这一道题需要注意什么?
探究新知
如图,做一个无盖的圆柱形铁皮水桶,底面直径为 4 dm,高为 5 dm,至少需要用多大面积的铁皮?
4 dm
5 dm
S表= S底+ S侧
S侧=
S底=
S表=
3.14×4×5=62.8(dm2)
3.14×(4÷2)2=12.56(dm2)
62.8+12.56=75.36(dm2)
答:至少需要75.36平方分米的铁皮。
探究新知
如图,把一个圆柱形薯片盒的商标纸展开,是一个长18.84cm,宽是10 cm的长方形。这个薯片盒的侧面积是多少?表面积呢?
S侧
S底
S底
10 cm
18.84 cm
C=18.84 cm
探究新知
如图,把一个圆柱形薯片盒的商标纸展开,是一个长18.84cm,宽是10 cm的长方形。这个薯片盒的侧面积是多少?表面积呢?
S侧=
18.84×10=188.4(cm2)
底面半径:
18.84÷3.14÷2=3(cm)
2S底=
3.14×32×2=56.52(cm2)
S表=
188.4+56.52=244.92(cm2)
答:这个薯片盒的侧面积是188.4cm2,表面积244.92cm2。
10 cm
18.84 cm
C=18.84 cm
探究新知
生活中,计算物体的表面积时,经常需要根据实际情况分析“需要计算哪些部分的面积”
玻璃杯的表面积
水桶的表面积
S表= S底+ S侧
1个侧面
1个底面
探究新知
柱子表面涂漆,求涂漆的面积。
求通风管所用材料的面积。
压路机前轮工作一圈的面积。
S表= S侧
1个侧面
课堂练习
1.填 空
(1)把圆柱的侧面沿着高剪开,可以得到一个( ),这个长方形的长等于圆柱的 ( ),宽等于圆柱的
( )
(2)当圆柱的底面周长和圆柱的高相等时,圆柱的侧面展开图是( )。
(3)圆柱有无数条( )。
(4)圆柱的侧面是一个( )。
长方形
底面周长
高
正方形
高
曲面
课堂练习
2.连一连,并在括号中填出相应的数。
( )
( )
( )
( )
9.42cm
8cm
3.14×3=9.42cm
21.98cm
4cm
3.14×7=21.98cm
8 cm
6 cm
课堂练习
3.求圆柱的表面积。
S表= 2S底+ S侧
S表= 2πr2 +πdh
= 3.14×(4÷2)2×2+4×3.14×6
= 100.48(cm2)
S表= 2S底+ S侧
S表= 2πr2 +2πrh
= 3.14×32×2+3×2×3.14×10
= 244.92(dm2)
课堂练习
4. 压路机前轮直径是1.6m,宽是2m,它转动一周,压路的面积是多少平方米?
3.14×1.6×2=10.048(m2)
答:压路的面积是10.048平方米。
前轮的侧面积
课堂练习
5. 一个圆柱形水池,水池内壁和底部都镶上瓷砖, 水池内部底面周长25.12m,池深1.2m,镶瓷砖的面积是多少平方米?
S表= S底+ S侧
S底=3.14×(25.12÷3.14÷2)2=50.24(m2)
S侧=25.12×1.2=30.144(m2)
S表=30.144+50.24=80.384(m2)
答:镶瓷砖的面积是80.384平方米。
课堂练习
6. 油桶的表面要刷上防锈油漆,每平方米需用防锈油漆0.2kg,刷一个油桶大约需要多少防锈油漆?(结果保留两位小数)
S表= 2S底+ S侧
S侧=3.14×0.6×1=1.884(m2)
2S底=3.14×(0.6÷2)2×2=0.5652(m2)
S表= 1.884+0.5652=2.4492(m2)
油漆:2.4492×0.2≈0.49(kg)
答:刷一个油桶大约需要0.49kg防锈油漆。
课堂总结
今天你有什么收获?
分层作业
【知识技能类作业】
1.判断。
(1)圆柱的侧面展开后一定是长方形。( )
(2)圆柱体的表面积=底面积×2+底面积×高( )
(3) 圆柱体的表面积一定比它的侧面积大。 ( )
(4)做一节圆柱形通风管要用多少铁皮,就是求它的侧面积。( )
x
x
√
x
分层作业
2.求下面圆柱的侧面积和表面积。
侧面积:3.14 x 4x2x8=200.96( cm2)
表面积:3.14 x 42x 2 +200.96= 301.44(cm2)
分层作业
3.填空。
(1)圆柱的底面半径扩大到原来的2倍,高不变,它的侧面积扩大到原来的( )倍。
A.2 B.4 C.6 D.8
(2)把一个底面积是 15.7cm 的圆柱切成3个同样大小的圆柱后,表面积增加了( )cm
A.15.7 B.31.4 C.47.1 D.62.8
A
D
分层作业
4.一个圆柱的侧面展开后是一个边长 31.4 dm 的正方形,这个圆柱的表面积是多少平方分米
31.4÷3.14÷2=5(dm)3.14x5 x2+31.4x31.4=1142.96(dm )
答:这个圆柱的表面积是 1142.96 dm 。
分层作业
5.如图,有一块长方形铁皮,涂色部分刚好能做成一个圆柱(接头处忽略不计),求这个圆柱的表面积。(提示:圆柱的底面周长等于长方形铁皮的长。)
底面半径:18.84÷3.14÷2=3(dm)
圆柱的高:10-3x2=4(dm)
圆柱的侧面积:18.84x 4=75.36( dm )
圆柱的表面积:75.36 +3.14 x 3 x 2=131.88( dm )答:这个圆柱的表面积是 131.88 dm 。
课堂练习
6. 做一做。
(1)找一个圆柱形物体,量出它的高和底面直径,计算出它的表面积。
(2)制作一个底面直径和高都是 10cm 的圆柱形纸盒。
【综合实践类作业】
https://www.21cnjy.com/help/help_extract.php
让备课更有效
www.21cnjy.com
Thanks!
