第七章 二次根式 综合测试卷(含答案)
文档属性
| 名称 | 第七章 二次根式 综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 368.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-05 15:01:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第七章综合测试卷
时间: 60分钟 满分: 100分.
一、选择题(每小题3分,共36分)
1.下列式子一定是二次根式的是 ( )
B.
2.下列代数式中,x能取一切实数的是 ( )
3.函数 的自变量的取值范围是 ( )
4.计算 的结果是 ( )
A.9 B.3
5.下列计算正确的是 ( )
6.在解决问题“已知 用含a,b的代数式表示. 时,甲的结果是 ;乙的结果是 ;丙的结果是 则下列说法正确的是 ( )
A.甲对 B.乙、丙对 C.甲、乙对 D.甲、乙、丙都对
7.计算 的结果是 ( )
8.如图,由两个直角三角形和三个正方形组成的图形,其中阴影部分两个正方形的面积分别为1和3, 则AC的长为 ( )
A.4 C.2 D.1
9.已知的关系是 ( )
10.估计 的值应在 ( )
A.8和9之间 B.9 和10之间 C.10 和11之间 D.11 和12之间
11.张老师在黑板上出了一道计算题: ○要求同学们在○中填入适当的运算符号,使得计算结果是有理数,○中可以填的符号是 ( )
A.×或÷ B.+或× C.+或÷ D.一或×
12.若 则 的值是 ( )
A.3 B.±3
二、填空题(每小题3分,共18分)
13.能使 成立的所有整数a的和是 .
14.已知 则 的值是 .
15.比较大小:
16.定义:若两个二次根式a,b满足,.且c是有理数,则称a与b是关于c 的共轭二次根式.
(1)若a与 是关于4的共轭二次根式,则a= ;
(2)若 与 是关于12的共轭二次根式,则m的值为 .
17.观察下列各式:
……则第7个等式是 .
18.阅读与计算:阅读以下材料,并完成相应的任务:斐波那契(约1170~1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列),后来人们研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰好是斐波那契数列中的数,斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用表示(其中n≥1),这是用无理数表示有理数的一个范例,请计算斐波那契数列中的第2个数的值是 .
三、解答题(共46分)
19.(6分)计算:
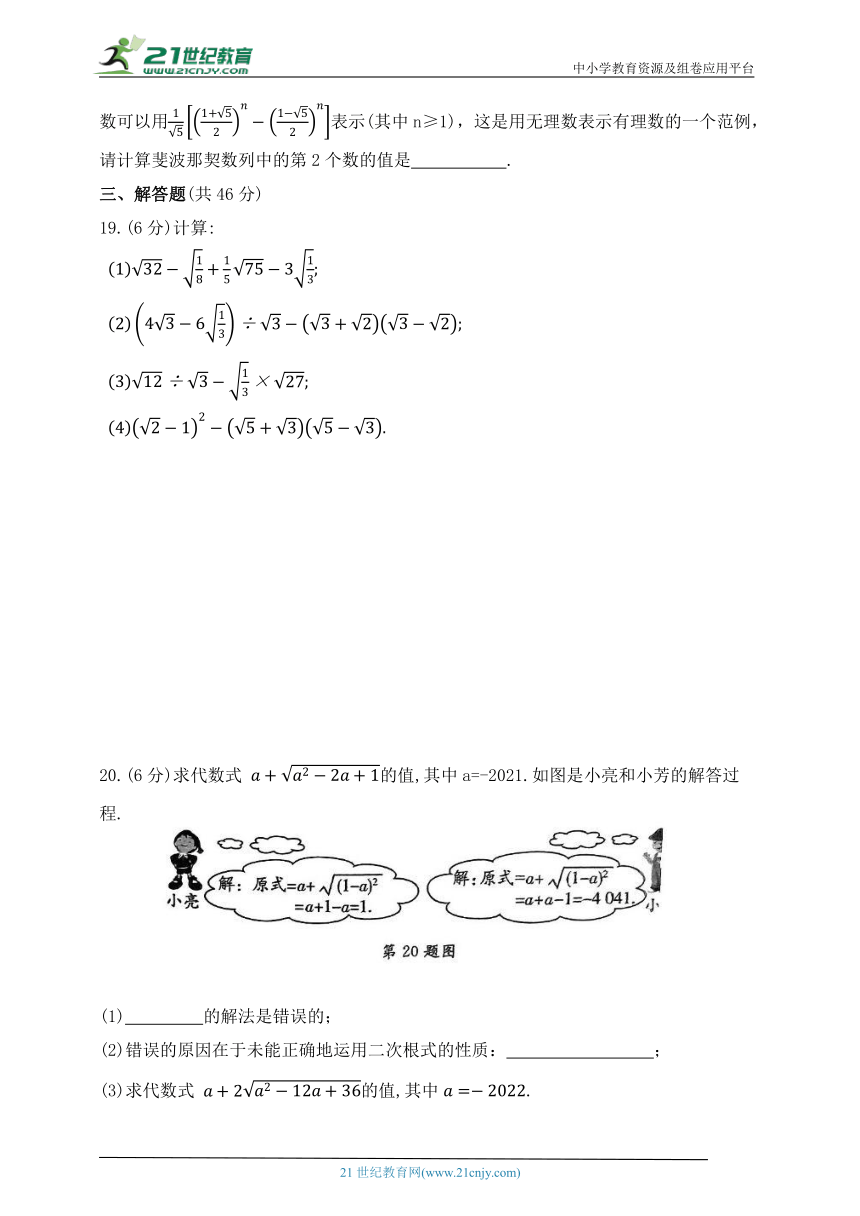
20.(6分)求代数式 的值,其中a=-2021.如图是小亮和小芳的解答过程.
(1) 的解法是错误的;
(2)错误的原因在于未能正确地运用二次根式的性质: ;
(3)求代数式 的值,其中.
21.(6分)观察下列等式:
(1)请你根据上述规律填空:
(2)①把你发现的规律用含有 n的等式表示出来:
②证明①中的等式是正确的,并注明n的取值范围.
22.(6分)在数学课外学习活动中,小明和他的同学遇到一道题:
已知求的值,他是这样解答的:
即
请你根据小明的解题过程,解决下列问题:
(2)化简
(3)若 求 的值.
23.(6分)据研究,高空抛物下落的时间t(单位:s)和高度h(单位:m)近似满足公式 (不考虑风速的影响).
(1)求从45 m高空抛物到落地时间;
(2)已知高空坠物动能W(单位: 物体质量(单位:kg)×高度(单位:m),某质量为0.1kg的玩具被抛出后经过4s后落在地上,这个玩具产生的动能会伤害到楼下的行人吗 请说明理由.(注:伤害无防护人体只需要65J的动能)
24.(8分)【阅读材料】
小明在学习二次根式时,发现一些含根号的式子可以化成另一个式子的平方,如:
【类比归纳】
(1)请你仿照小明的方法将 化成另一个式子的平方;
(2)请运用小明的方法化简:
【变式探究】
(3)若 且均为正整数,求的值.
25.(8分)(1)若a,b为实数,且 比较 与 的大小;
(2)在一般情况下,若a,b为实数,且 猜想 与 的大小关系,并证明你的结论.
参考答案
1. C 2. D 3. B 4. B 5. B 6. D
7. A 解析:
8. C 解析;如图,
∵阴影部分两个正方形的面积分别为1和3,AB=2 ∴EF =1,DF =3,
∵四边形BCDE 是正方形,△FED和△CAB都是直角三角形且∠EFD=90°,∠ACB=90°,
9. D 解析:a=2021×2023-2021×2022=2021×(2023-2022)=2021;
∵2 024 -4×2023=(2023+1) -4×2023=2023 +2×2023+1-4×2023=2022 ,∴b=2022;
10. C
11. B 解析: =4-5=-1,
4
:2
∴○中可以填的符号是+或×.
12. B 解析:
13.6 解析: 成立,
解得0≤a≤3,满足条件的所有整数为0,1,2,3,
∴它们的和为0+1+2+3=6.
14.8 解析: ),
=8.
15.
解析:①(5- )-(2+ )=3-2
∵ + > + ∴ .
16.(1)2 (2)-2
解析:(1)∵a与 是关于4的共轭二次根式,
与 是关于12的共轭二次根式,
∴m=-2.
解析:第1个等式
第 2 个 等 式:
第 3 个 等 式:
第 4 个 等 式:
…,
第 n 个等式 :
当n=7时
18. 1 解析: 第 2 个 数, 当 n = 2 时,
19.解:(1)原式
(2)原式 =2 ÷ -1=2-1=1;
(3)原式 =2-3=-1;
(4)原式=2-2 +1--(5-3)=3-2--2=1-2
20.解:(1)∵a=-2021,∴1-a=1-(-2 021)=1+2021=2022>0,
∴小芳的解法是错误的,故答案为:小芳;
当a=-2022时,a-6=-2022-6=-2028<0,
∴原式=a+2(6-a)=a+12-2a=-a+12=2022+12=2034,
∴代数式 的值为2034.
21.解:
②证明:等式左边右边,n为大于1的自然数.
22.解; 故答案为:
(2)原式
即
23.解:(1)由题意知
故从45 m高空抛物到落地时间为3s;
(2)这个玩具产生的动能会伤害到楼下的行人,理由:
当 时,
这个玩具产生的动能
∴这个玩具产生的动能会伤害到楼下的行人.
24.解:
或 ∴a=3+7=10或a=21+1=22.
25.解:(1)由条件,得 且 ∴a=±1,
∵a>0,∴a=1,∴b=4, +4=
∵3>
(2)当时, 证明:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章综合测试卷
时间: 60分钟 满分: 100分.
一、选择题(每小题3分,共36分)
1.下列式子一定是二次根式的是 ( )
B.
2.下列代数式中,x能取一切实数的是 ( )
3.函数 的自变量的取值范围是 ( )
4.计算 的结果是 ( )
A.9 B.3
5.下列计算正确的是 ( )
6.在解决问题“已知 用含a,b的代数式表示. 时,甲的结果是 ;乙的结果是 ;丙的结果是 则下列说法正确的是 ( )
A.甲对 B.乙、丙对 C.甲、乙对 D.甲、乙、丙都对
7.计算 的结果是 ( )
8.如图,由两个直角三角形和三个正方形组成的图形,其中阴影部分两个正方形的面积分别为1和3, 则AC的长为 ( )
A.4 C.2 D.1
9.已知的关系是 ( )
10.估计 的值应在 ( )
A.8和9之间 B.9 和10之间 C.10 和11之间 D.11 和12之间
11.张老师在黑板上出了一道计算题: ○要求同学们在○中填入适当的运算符号,使得计算结果是有理数,○中可以填的符号是 ( )
A.×或÷ B.+或× C.+或÷ D.一或×
12.若 则 的值是 ( )
A.3 B.±3
二、填空题(每小题3分,共18分)
13.能使 成立的所有整数a的和是 .
14.已知 则 的值是 .
15.比较大小:
16.定义:若两个二次根式a,b满足,.且c是有理数,则称a与b是关于c 的共轭二次根式.
(1)若a与 是关于4的共轭二次根式,则a= ;
(2)若 与 是关于12的共轭二次根式,则m的值为 .
17.观察下列各式:
……则第7个等式是 .
18.阅读与计算:阅读以下材料,并完成相应的任务:斐波那契(约1170~1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列),后来人们研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰好是斐波那契数列中的数,斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用表示(其中n≥1),这是用无理数表示有理数的一个范例,请计算斐波那契数列中的第2个数的值是 .
三、解答题(共46分)
19.(6分)计算:
20.(6分)求代数式 的值,其中a=-2021.如图是小亮和小芳的解答过程.
(1) 的解法是错误的;
(2)错误的原因在于未能正确地运用二次根式的性质: ;
(3)求代数式 的值,其中.
21.(6分)观察下列等式:
(1)请你根据上述规律填空:
(2)①把你发现的规律用含有 n的等式表示出来:
②证明①中的等式是正确的,并注明n的取值范围.
22.(6分)在数学课外学习活动中,小明和他的同学遇到一道题:
已知求的值,他是这样解答的:
即
请你根据小明的解题过程,解决下列问题:
(2)化简
(3)若 求 的值.
23.(6分)据研究,高空抛物下落的时间t(单位:s)和高度h(单位:m)近似满足公式 (不考虑风速的影响).
(1)求从45 m高空抛物到落地时间;
(2)已知高空坠物动能W(单位: 物体质量(单位:kg)×高度(单位:m),某质量为0.1kg的玩具被抛出后经过4s后落在地上,这个玩具产生的动能会伤害到楼下的行人吗 请说明理由.(注:伤害无防护人体只需要65J的动能)
24.(8分)【阅读材料】
小明在学习二次根式时,发现一些含根号的式子可以化成另一个式子的平方,如:
【类比归纳】
(1)请你仿照小明的方法将 化成另一个式子的平方;
(2)请运用小明的方法化简:
【变式探究】
(3)若 且均为正整数,求的值.
25.(8分)(1)若a,b为实数,且 比较 与 的大小;
(2)在一般情况下,若a,b为实数,且 猜想 与 的大小关系,并证明你的结论.
参考答案
1. C 2. D 3. B 4. B 5. B 6. D
7. A 解析:
8. C 解析;如图,
∵阴影部分两个正方形的面积分别为1和3,AB=2 ∴EF =1,DF =3,
∵四边形BCDE 是正方形,△FED和△CAB都是直角三角形且∠EFD=90°,∠ACB=90°,
9. D 解析:a=2021×2023-2021×2022=2021×(2023-2022)=2021;
∵2 024 -4×2023=(2023+1) -4×2023=2023 +2×2023+1-4×2023=2022 ,∴b=2022;
10. C
11. B 解析: =4-5=-1,
4
:2
∴○中可以填的符号是+或×.
12. B 解析:
13.6 解析: 成立,
解得0≤a≤3,满足条件的所有整数为0,1,2,3,
∴它们的和为0+1+2+3=6.
14.8 解析: ),
=8.
15.
解析:①(5- )-(2+ )=3-2
∵ + > + ∴ .
16.(1)2 (2)-2
解析:(1)∵a与 是关于4的共轭二次根式,
与 是关于12的共轭二次根式,
∴m=-2.
解析:第1个等式
第 2 个 等 式:
第 3 个 等 式:
第 4 个 等 式:
…,
第 n 个等式 :
当n=7时
18. 1 解析: 第 2 个 数, 当 n = 2 时,
19.解:(1)原式
(2)原式 =2 ÷ -1=2-1=1;
(3)原式 =2-3=-1;
(4)原式=2-2 +1--(5-3)=3-2--2=1-2
20.解:(1)∵a=-2021,∴1-a=1-(-2 021)=1+2021=2022>0,
∴小芳的解法是错误的,故答案为:小芳;
当a=-2022时,a-6=-2022-6=-2028<0,
∴原式=a+2(6-a)=a+12-2a=-a+12=2022+12=2034,
∴代数式 的值为2034.
21.解:
②证明:等式左边右边,n为大于1的自然数.
22.解; 故答案为:
(2)原式
即
23.解:(1)由题意知
故从45 m高空抛物到落地时间为3s;
(2)这个玩具产生的动能会伤害到楼下的行人,理由:
当 时,
这个玩具产生的动能
∴这个玩具产生的动能会伤害到楼下的行人.
24.解:
或 ∴a=3+7=10或a=21+1=22.
25.解:(1)由条件,得 且 ∴a=±1,
∵a>0,∴a=1,∴b=4, +4=
∵3>
(2)当时, 证明:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
