7.2.3.1 平行线的性质 课件(共27张PPT)【2025春人教新版七下数学情境课堂课件】
文档属性
| 名称 | 7.2.3.1 平行线的性质 课件(共27张PPT)【2025春人教新版七下数学情境课堂课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-05 16:12:25 | ||
图片预览







文档简介
(共27张PPT)
统编2024七下数学同步精品课件
人教版七年级下册
相交线与平行线
2025年春七下历史情景教学课件嵌视频(统编2024版)
第七单元 相交线与平行线
7.2 平行线
7.2.3.1 平行线的性质
1. 掌握平行线的性质,会运用两条直线平行判断角相等或互补.
2. 能根据平行线的性质进行简单的推理.
学习目标
新课引入
利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行. 那么当两条直线平行时,同位角、内错角、同旁内角各有什么关系呢?
将条件和结论反过来,它还成立吗?
同位角相等
内错角相等
同旁内角互补
条件
结论
两直线平行
新知学习
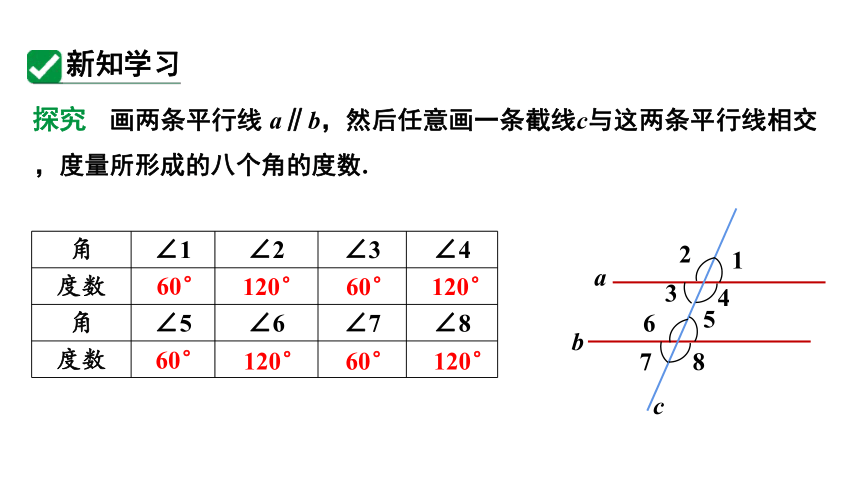
画两条平行线 a∥b,然后任意画一条截线c与这两条平行线相交,度量所形成的八个角的度数.
探究
b
1
2
a
c
5
6
7
8
3
4
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
60°
60°
60°
60°
120°
120°
120°
120°
(1)在∠1,∠2,…,∠8 中,哪些是同位角 它们的度数有什么关系
b
1
2
a
c
5
6
7
8
3
4
猜想:两条平行线被第三条直线所截,同位角相等.
同位角∠1=∠5,∠4=∠8,∠2=∠6,∠3=∠7
(2)改变截线c的位置,同样度量并比较各对同位角的度数,你的猜想还成立吗
猜想成立.
同位角∠1=∠5,
1
5
2
4
3
6
7
8
∠4=∠8,
∠2=∠6,
∠3=∠7;
b
a
c
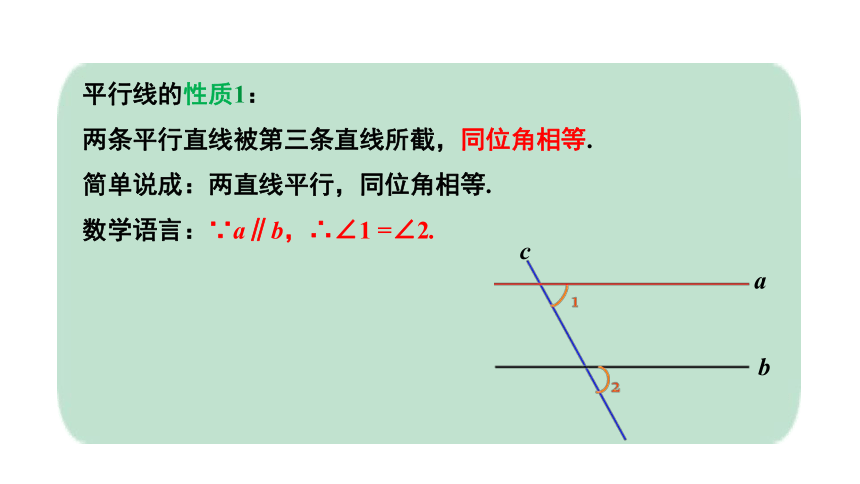
平行线的性质1:
两条平行直线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
数学语言:∵a∥b,∴∠1 =∠2.
a
b
c
例1 (2024重庆)如图,AB∥CD,∠1=65°,则∠2的度数是( )
A. 105° B. 115°
C. 125° D. 135°
B
C
D
A
B
2
1
思 考
前面我们利用 “同位角相等,两直线平行” 推出了 “内错角相等,两直线平行”. 类似地,你能由性质1推出两条平行线被第三条直线截得的内错角之间的关系吗
a
b
c
如果a∥b,能否得到∠1 =∠3 ?
探 究
a
b
c
1
2
3
4
(1)如图,当直线a∥b、c是截线时,内错角∠1=∠2吗
因为a∥b,
所以∠1=∠4(两直线平行,同位角相等),
又因为∠4=∠2(对顶角相等),
所以∠1=∠2.
平行线的性质2:
两条平行直线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
数学语言:∵ a∥b,∴∠2 =∠3.
a
b
c
3
例2 一辆汽车经过一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行. 第一次拐的∠B 等于142°,第二次拐的∠C 的度数是_____.
142°
a
b
c
1
2
3
4
(2)如图,当直线a∥b、c是截线时,同旁内角∠1与∠3互补吗
方法1:
因为a∥b,
所以∠1=∠4(两直线平行,同位角相等),
又因为∠3+∠4=180°,
所以∠1+∠3=180°,
所以∠1与∠3互补.
探 究
a
b
c
1
2
3
4
方法2:
因为a∥b,
所以∠1=∠2(两直线平行,内错角相等),
又因为∠2+∠3=180°,
所以∠1+∠3=180°,
所以∠1与∠3互补.
(2)如图,当直线a∥b、c是截线时,同旁内角∠1与∠3互补吗
平行线的性质3:
两条平行直线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
数学语言:∵ a∥b,∴∠1+∠4 = 180°.
a
b
c
3
4
例3 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角∠D,∠C分别是多少度
解:因为梯形上、下两底DC与 AB互相平行.
根据 “两直线平行,同旁内角互补”, 可得
∠A 与∠D互补,∠ B 与∠C互补.
于是∠D=180°-∠A = 180°-100°=80°,
∠C= 180°-∠B= 180°-115°=65°.
所以梯形的另外两个角∠D,∠C分别是80°,65°.
A
B
C
D
随堂练习
1.(2024苏州)如图,AB∥CD,若∠1=65°,∠2=120°,则∠3的度数为( )
A. 45° B. 55°
C. 60° D. 65°
B
2.(2024达州)当光线从空气射入水中时,光线的传播方向发生了改变,这就是光的折射现象(如图所示). 图中∠1=80°,∠2=40°,则∠3的度数为( )
A. 30° B. 40°
C. 50° D. 70°
B
3.(2024盐城)小明将一块直角三角板摆放在直尺上,如图,若∠1=55°,则∠2的度数为( )
B
A. 25° B. 35°
C. 45° D. 55°
4.(2024陕西)如图,AB∥DC,BC∥DE,∠B=145°,则∠D的度数为( )
A. 25° B. 35°
C. 45° D. 55°
B
C
D
A
B
E
5. 如图,直线 a∥b,∠1 = 54°,∠2、∠3、∠4 各是多少度?
a
b
解:∠2 = ∠1 = 54°(对顶角相等);
因为a∥b,
所以∠3 =180°- ∠2 =180°- 54°= 126°,
(两直线平行,同旁内角互补).
∠4 =∠2 = 54°(两直线平行,内错角相等).
6. 如图,AB∥CD,EF∥MN,找出一些与∠1相等或成互补的角.
解:∠1=∠2 (两直线平行,内错角相等);
A
C
1
B
D
2
∠1与∠4互补,∠1与∠9互补(两直线平行,同旁内角互补);
∠1与∠5互补,∠1与∠6互补(邻补角互补).
∠1=∠3 ,∠1=∠8(两直线平行,同位角相等);
∠1=∠7 (对顶角相等);
E
F
M
N
3
4
6
7
5
8
9
平行线的性质
性质1
课堂小结
性质2
性质3
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
统编2024七下数学同步精品课件
人教版七年级下册
相交线与平行线
2025年春七下历史情景教学课件嵌视频(统编2024版)
第七单元 相交线与平行线
7.2 平行线
7.2.3.1 平行线的性质
1. 掌握平行线的性质,会运用两条直线平行判断角相等或互补.
2. 能根据平行线的性质进行简单的推理.
学习目标
新课引入
利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行. 那么当两条直线平行时,同位角、内错角、同旁内角各有什么关系呢?
将条件和结论反过来,它还成立吗?
同位角相等
内错角相等
同旁内角互补
条件
结论
两直线平行
新知学习
画两条平行线 a∥b,然后任意画一条截线c与这两条平行线相交,度量所形成的八个角的度数.
探究
b
1
2
a
c
5
6
7
8
3
4
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
60°
60°
60°
60°
120°
120°
120°
120°
(1)在∠1,∠2,…,∠8 中,哪些是同位角 它们的度数有什么关系
b
1
2
a
c
5
6
7
8
3
4
猜想:两条平行线被第三条直线所截,同位角相等.
同位角∠1=∠5,∠4=∠8,∠2=∠6,∠3=∠7
(2)改变截线c的位置,同样度量并比较各对同位角的度数,你的猜想还成立吗
猜想成立.
同位角∠1=∠5,
1
5
2
4
3
6
7
8
∠4=∠8,
∠2=∠6,
∠3=∠7;
b
a
c
平行线的性质1:
两条平行直线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
数学语言:∵a∥b,∴∠1 =∠2.
a
b
c
例1 (2024重庆)如图,AB∥CD,∠1=65°,则∠2的度数是( )
A. 105° B. 115°
C. 125° D. 135°
B
C
D
A
B
2
1
思 考
前面我们利用 “同位角相等,两直线平行” 推出了 “内错角相等,两直线平行”. 类似地,你能由性质1推出两条平行线被第三条直线截得的内错角之间的关系吗
a
b
c
如果a∥b,能否得到∠1 =∠3 ?
探 究
a
b
c
1
2
3
4
(1)如图,当直线a∥b、c是截线时,内错角∠1=∠2吗
因为a∥b,
所以∠1=∠4(两直线平行,同位角相等),
又因为∠4=∠2(对顶角相等),
所以∠1=∠2.
平行线的性质2:
两条平行直线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
数学语言:∵ a∥b,∴∠2 =∠3.
a
b
c
3
例2 一辆汽车经过一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行. 第一次拐的∠B 等于142°,第二次拐的∠C 的度数是_____.
142°
a
b
c
1
2
3
4
(2)如图,当直线a∥b、c是截线时,同旁内角∠1与∠3互补吗
方法1:
因为a∥b,
所以∠1=∠4(两直线平行,同位角相等),
又因为∠3+∠4=180°,
所以∠1+∠3=180°,
所以∠1与∠3互补.
探 究
a
b
c
1
2
3
4
方法2:
因为a∥b,
所以∠1=∠2(两直线平行,内错角相等),
又因为∠2+∠3=180°,
所以∠1+∠3=180°,
所以∠1与∠3互补.
(2)如图,当直线a∥b、c是截线时,同旁内角∠1与∠3互补吗
平行线的性质3:
两条平行直线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
数学语言:∵ a∥b,∴∠1+∠4 = 180°.
a
b
c
3
4
例3 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角∠D,∠C分别是多少度
解:因为梯形上、下两底DC与 AB互相平行.
根据 “两直线平行,同旁内角互补”, 可得
∠A 与∠D互补,∠ B 与∠C互补.
于是∠D=180°-∠A = 180°-100°=80°,
∠C= 180°-∠B= 180°-115°=65°.
所以梯形的另外两个角∠D,∠C分别是80°,65°.
A
B
C
D
随堂练习
1.(2024苏州)如图,AB∥CD,若∠1=65°,∠2=120°,则∠3的度数为( )
A. 45° B. 55°
C. 60° D. 65°
B
2.(2024达州)当光线从空气射入水中时,光线的传播方向发生了改变,这就是光的折射现象(如图所示). 图中∠1=80°,∠2=40°,则∠3的度数为( )
A. 30° B. 40°
C. 50° D. 70°
B
3.(2024盐城)小明将一块直角三角板摆放在直尺上,如图,若∠1=55°,则∠2的度数为( )
B
A. 25° B. 35°
C. 45° D. 55°
4.(2024陕西)如图,AB∥DC,BC∥DE,∠B=145°,则∠D的度数为( )
A. 25° B. 35°
C. 45° D. 55°
B
C
D
A
B
E
5. 如图,直线 a∥b,∠1 = 54°,∠2、∠3、∠4 各是多少度?
a
b
解:∠2 = ∠1 = 54°(对顶角相等);
因为a∥b,
所以∠3 =180°- ∠2 =180°- 54°= 126°,
(两直线平行,同旁内角互补).
∠4 =∠2 = 54°(两直线平行,内错角相等).
6. 如图,AB∥CD,EF∥MN,找出一些与∠1相等或成互补的角.
解:∠1=∠2 (两直线平行,内错角相等);
A
C
1
B
D
2
∠1与∠4互补,∠1与∠9互补(两直线平行,同旁内角互补);
∠1与∠5互补,∠1与∠6互补(邻补角互补).
∠1=∠3 ,∠1=∠8(两直线平行,同位角相等);
∠1=∠7 (对顶角相等);
E
F
M
N
3
4
6
7
5
8
9
平行线的性质
性质1
课堂小结
性质2
性质3
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
