7.2.3.2 平行线判定与性质的综合应用(主题情境:台风天加固窗户) 课件(共23张PPT)【2025春人教新版七下数学情境课堂课件】
文档属性
| 名称 | 7.2.3.2 平行线判定与性质的综合应用(主题情境:台风天加固窗户) 课件(共23张PPT)【2025春人教新版七下数学情境课堂课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-05 16:13:46 | ||
图片预览







文档简介
(共23张PPT)
统编2024七下数学同步精品课件
人教版七年级下册
相交线与平行线
2025年春七下历史情景教学课件嵌视频(统编2024版)
第七单元 相交线与平行线
7.2 平行线
7.2.3.2 平行线判定与性质的综合应用
学习目标
1. 进一步熟悉平行线的判定方法和性质.
2. 能够综合应用平行线的判定和性质进行推理解决问题.
在台风季节来临之际,为了确保居民的安全,社区决定对每户人家的窗户进行加固. 如何帮助居民们正确地加固窗户,防止台风带来的强风将窗户吹破呢?
情境学新知
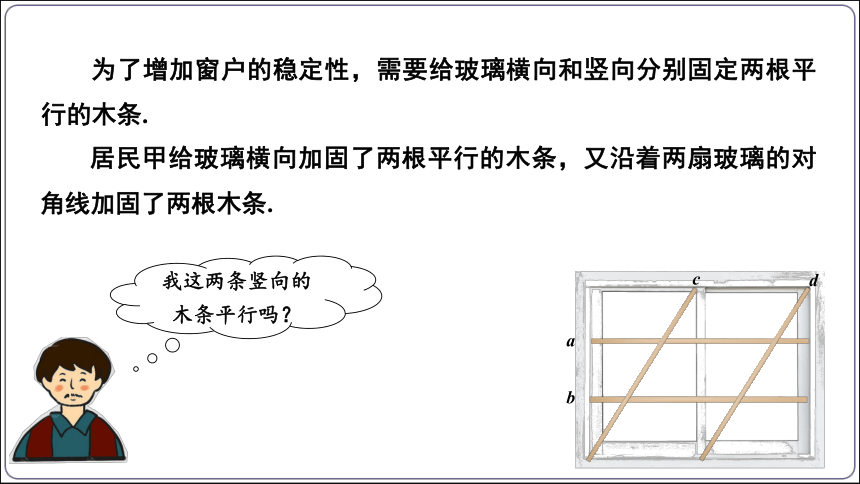
为了增加窗户的稳定性,需要给玻璃横向和竖向分别固定两根平行的木条.
我这两条竖向的木条平行吗?
a
b
c
d
居民甲给玻璃横向加固了两根平行的木条,又沿着两扇玻璃的对角线加固了两根木条.
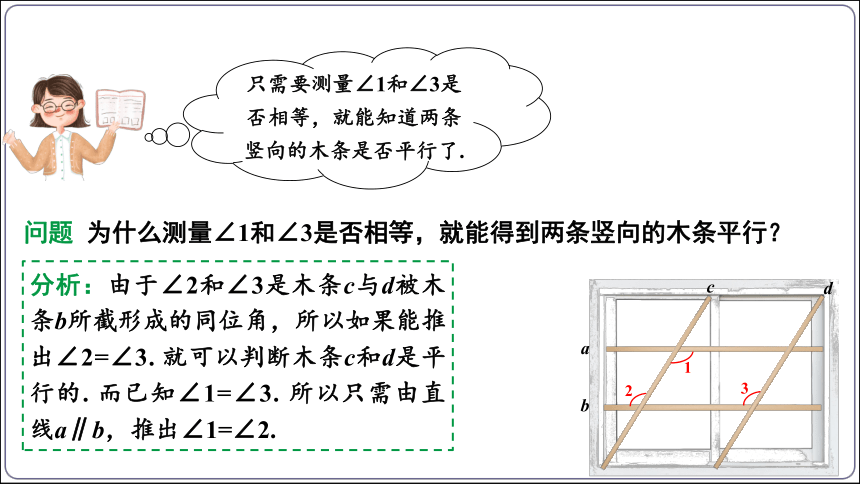
只需要测量∠1和∠3是否相等,就能知道两条竖向的木条是否平行了.
问题 为什么测量∠1和∠3是否相等,就能得到两条竖向的木条平行?
1
2
3
a
b
c
d
分析:由于∠2和∠3是木条c与d被木条b所截形成的同位角,所以如果能推出∠2=∠3. 就可以判断木条c和d是平行的. 而已知∠1=∠3. 所以只需由直线a∥b,推出∠1=∠2.
问题 为什么测量∠1和∠3是否相等,就能得到两条竖向的木条平行?
1
2
3
a
b
c
d
解:∵a∥b.
∴∠1=∠2 (两直线平行,内错角相等).
又∠1=∠3.
∴∠2=∠3.
∴c∥d (同位角相等,两直线平行).
思考 你能用其他方法判定两条竖向木条平行吗?
1
2
3
a
b
c
d
4
解:∵a∥b.
∴∠1=∠4 (两直线平行,同位角相等).
又∠1=∠3.
∴∠3=∠4.
∴c∥d (内错角相等,两直线平行).
居民乙决定采用“米字加固法”,在给玻璃横向和竖向分别固定两根木条的基础上增加两根斜着的木条形成交叉支撑结构,更有效的分散风力,减少窗户因受到集中力而破裂的风险.
a
b
e
f
c
d
由于45°的夹角能够使交叉的木条
更有效地抵抗风力作用,提高窗户的稳
定性和抗风能力,所以我在钉木条的时候使木条e与木条c、木条f与木条d的夹角
分别为45°.
问题 已知∠5=∠6,∠7=60°,则木条c与木条b的夹角∠OCD的度数是多少?木条e与木条b的夹角呢?
7
a
b
e
f
c
d
O
A
B
C
D
5
6
解:∵∠5=∠6,
∴a∥b(内错角相等,两直线平行),
∴∠7=∠OCD(两直线平行,同位角相等),
又∠7=60°,∴∠OCD=60°.
由木条c与木条e的夹角可得:∠COD=45°.
在△COD中,∠COD=45°,∠OCD = 60°
∴∠ODC=180°- 45°- 60°= 75°,
综上:木条c与木条b的夹角为60°;木条e与木条b的夹角为75°.
思考 若木条c平行于木条d,那么木条e与木条f 平行吗?
解:木条e与木条f 平行,理由如下:
∵c∥d,
∴∠OCD=∠EFG =60°(两直线平行,同位角相等),在△EFG中,∠FEG=45°,∠EFG=60°,
∴∠EGF= 75°.
又∵∠ODC= 75°,
∴ e∥f (同位角相等,两直线平行).
7
a
b
e
f
c
d
O
A
B
C
D
5
6
E
F
G
随堂练习
1.如图,这是小康设计的一个纸风车的示意图,其中AB与CD的交点O
在风车杆上,若∠A=∠B=56°,∠D=84°,则∠C的度数为( )
A.56° B.64°
C.76° D.84°
D
2.如图,CB∥DE,∠D+∠B=180°.请说明:AB∥CD.以下是排乱的解题过程:①∵∠D+∠B=180°;②∴∠D+∠C=180°③∴AB∥CD;④∵CB∥DE;⑤∴∠B=∠C,正确的顺序应是( )
B
A.①②③④⑤ B.④②①⑤③
C.④⑤①②③ D.①②④⑤③
A
B
C
D
E
3.义乌市为了方便市民绿色行,推出了如图①所示的某品牌共享单车,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=62°,∠BAC=53°,当∠MAC为( )度时,AM与CB平行.
A.62 B.65 C.75 D.115
B
图①
图②
4.(2024呼和浩特)如图,直线l1和l2被直线l3和l4所截,∠1=∠2=130°,∠3=75°,则∠4的度数为( )
A.75° B.105°
C.115° D.130°
B
5.如图EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
解:∵EF∥AD,
∴∠2=______,
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥_____,
∴∠BAC+_______=180° ________________________,
∵∠BAC=70°,∴∠AGD=_________.
110°
G
F
E
D
C
B
A
3
2
1
DG
∠AGD
∠3
两直线平行,同旁内角互补
6.(2024自贡节选)如图,在△ABC中,DE∥BC,∠EDF=∠C.
∠BDF和∠A相等吗?
解:∠BDF和∠A相等,理由如下:
由题意可知:DE∥BC,
∴∠C=∠AED (两直线平行,同位角相等),
∵∠EDF=∠C,
∴∠AED=∠EDF,
∴DF∥AC (内错角相等,两直线平行),
∴∠BDF=∠A(两直线平行,同位角相等).
A
B
C
D
E
F
7.如图是一种躺椅及其简化结构示意图,扶手AB与底座CD都平行于地面EF,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,∠AOE=∠BNM.
(1)请说明:OE∥DM;
解:∵∠BNM=∠AND,∠AOE=∠BNM,
∴∠AOE=∠AND,
∴OE∥DM;
7.(2)若OE平分∠AOF,∠ODC=30°,求扶手AB与靠背DM的夹角∠ANM 的度数.
解:∵AB与底座CD都平行于地面EF,
∴AB∥CD,
∴∠AOF+∠ODC=180°,
∴∠AOF=150°,
∵OE平分∠AOF,
∴∠AOE=∠AOF=75°,
∵OE∥DM,
∴∠AOE=∠AND=75°,
∴∠ANM=180°-∠AND=105°.
课堂小结
同位角相等
内错角相等
同旁内角互补
两直线平行
判 定
性 质
已 知
已 知
得 到
得 到
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
统编2024七下数学同步精品课件
人教版七年级下册
相交线与平行线
2025年春七下历史情景教学课件嵌视频(统编2024版)
第七单元 相交线与平行线
7.2 平行线
7.2.3.2 平行线判定与性质的综合应用
学习目标
1. 进一步熟悉平行线的判定方法和性质.
2. 能够综合应用平行线的判定和性质进行推理解决问题.
在台风季节来临之际,为了确保居民的安全,社区决定对每户人家的窗户进行加固. 如何帮助居民们正确地加固窗户,防止台风带来的强风将窗户吹破呢?
情境学新知
为了增加窗户的稳定性,需要给玻璃横向和竖向分别固定两根平行的木条.
我这两条竖向的木条平行吗?
a
b
c
d
居民甲给玻璃横向加固了两根平行的木条,又沿着两扇玻璃的对角线加固了两根木条.
只需要测量∠1和∠3是否相等,就能知道两条竖向的木条是否平行了.
问题 为什么测量∠1和∠3是否相等,就能得到两条竖向的木条平行?
1
2
3
a
b
c
d
分析:由于∠2和∠3是木条c与d被木条b所截形成的同位角,所以如果能推出∠2=∠3. 就可以判断木条c和d是平行的. 而已知∠1=∠3. 所以只需由直线a∥b,推出∠1=∠2.
问题 为什么测量∠1和∠3是否相等,就能得到两条竖向的木条平行?
1
2
3
a
b
c
d
解:∵a∥b.
∴∠1=∠2 (两直线平行,内错角相等).
又∠1=∠3.
∴∠2=∠3.
∴c∥d (同位角相等,两直线平行).
思考 你能用其他方法判定两条竖向木条平行吗?
1
2
3
a
b
c
d
4
解:∵a∥b.
∴∠1=∠4 (两直线平行,同位角相等).
又∠1=∠3.
∴∠3=∠4.
∴c∥d (内错角相等,两直线平行).
居民乙决定采用“米字加固法”,在给玻璃横向和竖向分别固定两根木条的基础上增加两根斜着的木条形成交叉支撑结构,更有效的分散风力,减少窗户因受到集中力而破裂的风险.
a
b
e
f
c
d
由于45°的夹角能够使交叉的木条
更有效地抵抗风力作用,提高窗户的稳
定性和抗风能力,所以我在钉木条的时候使木条e与木条c、木条f与木条d的夹角
分别为45°.
问题 已知∠5=∠6,∠7=60°,则木条c与木条b的夹角∠OCD的度数是多少?木条e与木条b的夹角呢?
7
a
b
e
f
c
d
O
A
B
C
D
5
6
解:∵∠5=∠6,
∴a∥b(内错角相等,两直线平行),
∴∠7=∠OCD(两直线平行,同位角相等),
又∠7=60°,∴∠OCD=60°.
由木条c与木条e的夹角可得:∠COD=45°.
在△COD中,∠COD=45°,∠OCD = 60°
∴∠ODC=180°- 45°- 60°= 75°,
综上:木条c与木条b的夹角为60°;木条e与木条b的夹角为75°.
思考 若木条c平行于木条d,那么木条e与木条f 平行吗?
解:木条e与木条f 平行,理由如下:
∵c∥d,
∴∠OCD=∠EFG =60°(两直线平行,同位角相等),在△EFG中,∠FEG=45°,∠EFG=60°,
∴∠EGF= 75°.
又∵∠ODC= 75°,
∴ e∥f (同位角相等,两直线平行).
7
a
b
e
f
c
d
O
A
B
C
D
5
6
E
F
G
随堂练习
1.如图,这是小康设计的一个纸风车的示意图,其中AB与CD的交点O
在风车杆上,若∠A=∠B=56°,∠D=84°,则∠C的度数为( )
A.56° B.64°
C.76° D.84°
D
2.如图,CB∥DE,∠D+∠B=180°.请说明:AB∥CD.以下是排乱的解题过程:①∵∠D+∠B=180°;②∴∠D+∠C=180°③∴AB∥CD;④∵CB∥DE;⑤∴∠B=∠C,正确的顺序应是( )
B
A.①②③④⑤ B.④②①⑤③
C.④⑤①②③ D.①②④⑤③
A
B
C
D
E
3.义乌市为了方便市民绿色行,推出了如图①所示的某品牌共享单车,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=62°,∠BAC=53°,当∠MAC为( )度时,AM与CB平行.
A.62 B.65 C.75 D.115
B
图①
图②
4.(2024呼和浩特)如图,直线l1和l2被直线l3和l4所截,∠1=∠2=130°,∠3=75°,则∠4的度数为( )
A.75° B.105°
C.115° D.130°
B
5.如图EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
解:∵EF∥AD,
∴∠2=______,
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥_____,
∴∠BAC+_______=180° ________________________,
∵∠BAC=70°,∴∠AGD=_________.
110°
G
F
E
D
C
B
A
3
2
1
DG
∠AGD
∠3
两直线平行,同旁内角互补
6.(2024自贡节选)如图,在△ABC中,DE∥BC,∠EDF=∠C.
∠BDF和∠A相等吗?
解:∠BDF和∠A相等,理由如下:
由题意可知:DE∥BC,
∴∠C=∠AED (两直线平行,同位角相等),
∵∠EDF=∠C,
∴∠AED=∠EDF,
∴DF∥AC (内错角相等,两直线平行),
∴∠BDF=∠A(两直线平行,同位角相等).
A
B
C
D
E
F
7.如图是一种躺椅及其简化结构示意图,扶手AB与底座CD都平行于地面EF,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,∠AOE=∠BNM.
(1)请说明:OE∥DM;
解:∵∠BNM=∠AND,∠AOE=∠BNM,
∴∠AOE=∠AND,
∴OE∥DM;
7.(2)若OE平分∠AOF,∠ODC=30°,求扶手AB与靠背DM的夹角∠ANM 的度数.
解:∵AB与底座CD都平行于地面EF,
∴AB∥CD,
∴∠AOF+∠ODC=180°,
∴∠AOF=150°,
∵OE平分∠AOF,
∴∠AOE=∠AOF=75°,
∵OE∥DM,
∴∠AOE=∠AND=75°,
∴∠ANM=180°-∠AND=105°.
课堂小结
同位角相等
内错角相等
同旁内角互补
两直线平行
判 定
性 质
已 知
已 知
得 到
得 到
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
