人教版九年级数学下册 27.2.1 相似三角形的判定 同步练习(含详解)
文档属性
| 名称 | 人教版九年级数学下册 27.2.1 相似三角形的判定 同步练习(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 791.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-05 17:31:08 | ||
图片预览




文档简介
27.2.1 相似三角形的判定
一、单选题
1.如图在正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与相似的三角形所在的网格图形是( )
A. B. C. D.
2.如图,小正方形的边长均为1,则图中三角形(阴影部分)与相似的是( )
A. B. C. D.
3.如图所示,网格中相似的两个三角形是( )
A.①与② B.①与③ C.③与④ D.②与③
4.如图,在四边形ABDC中,不等长的两对角线AD、BC相交于O点,且将四边形ABDC分成甲、乙、丙、丁四个三角形.若OA:OB=OC:OD=2:3,则此四个三角形的关系,下列叙述正确的是( )
A.甲与丙相似,乙与丁相似
B.甲与丙相似,乙与丁不相似
C.甲与丙不相似,乙与丁相似
D.甲与丙不相似,乙与丁不相似
5.如图,在正方形网格中有5个格点三角形,分别是:①,②,③,④,⑤,其中与⑤相似的三角形是( )
A.①③ B.①④ C.②④ D.①③④
6.如图,在中,P、Q分别为AB、AC边上的点,且满足.根据以上信息,嘉嘉和淇淇给出了下列结论:
嘉嘉说:连接PQ,则PQ//BC.
淇淇说:.
对于嘉嘉和淇淇的结论,下列判断正确的是( )
A.嘉嘉正确,淇淇错误 B.嘉嘉错误,淇淇正确
C.两人都正确 D.两人都错误
7.如图,在三角形纸片ABC中,,,,沿虚线剪下的涂色部分的三角形与△ABC相似的是( )
A.B.C.D.
8.如图,已知点D是的边上的一点,根据下列条件,可以得到的是( )
A. B.
C. D.
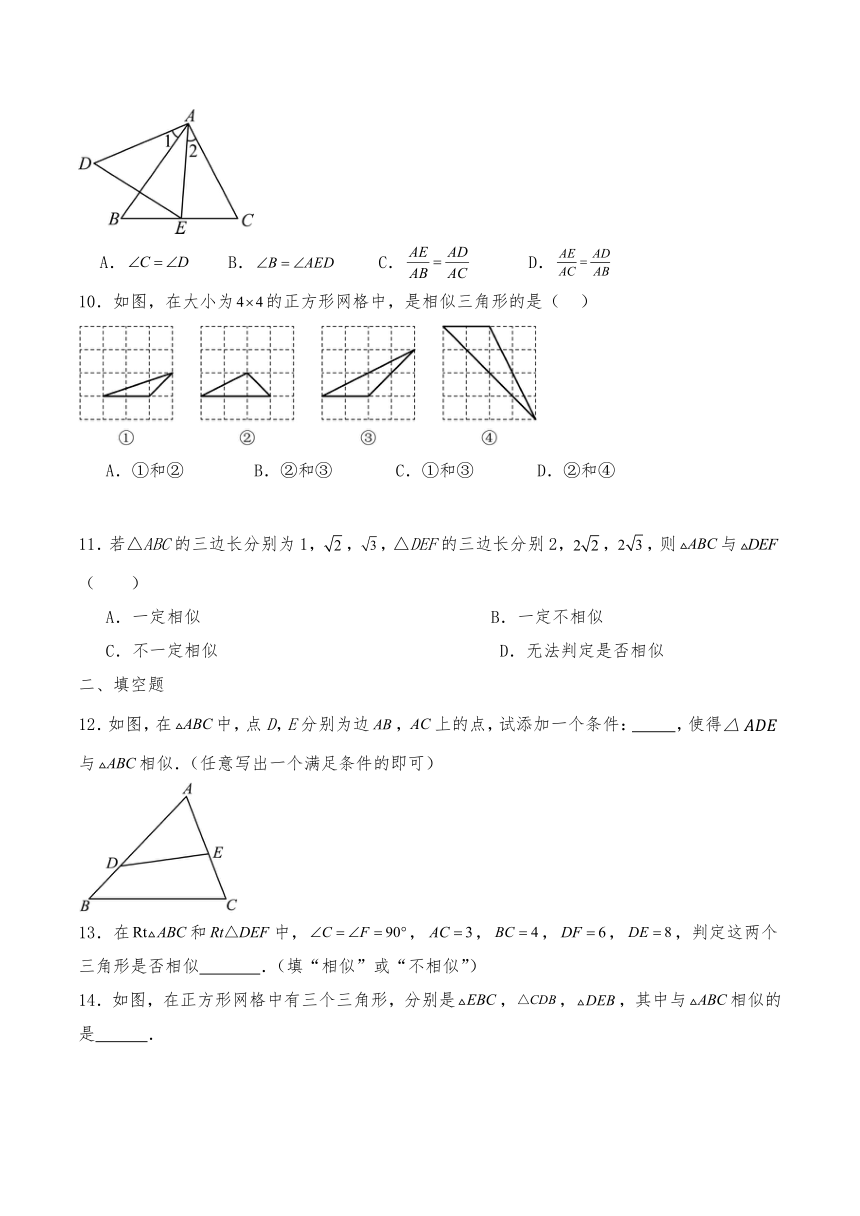
9.如图,,如果增加一个条件就能使结论成立,那么这个条件可以是( )
A. B. C. D.
10.如图,在大小为的正方形网格中,是相似三角形的是( )
A.①和② B.②和③ C.①和③ D.②和④
11.若△ABC的三边长分别为1,,,△DEF的三边长分别2,,,则与( )
A.一定相似 B.一定不相似
C.不一定相似 D.无法判定是否相似
二、填空题
12.如图,在中,点D,E分别为边,上的点,试添加一个条件: ,使得与相似.(任意写出一个满足条件的即可)
13.在和中,,,,,,判定这两个三角形是否相似 .(填“相似”或“不相似”)
14.如图,在正方形网格中有三个三角形,分别是,,,其中与相似的是 .
15.相似三角形的判定:
(1)平行于三角形一边的直线与其他两边(或 )相交,截得的三角形与原三角形相似.
(2)两组角对应 ,两三角形相似.
(3)两边对应成比例且 相等,两三角形相似.
(4)三边对应 ,两三角形相似.
16.如图,已知,则的度数为 .
17.如图,AC与BD相交于点O,在△AOB和△DOC中,已知,又因为 ,可证明△AOB∽△DOC.
18.的三边长分别为6、8、12,的三边长分别为2、3、2.5,的三边长分别为6、3、4,则与 相似.
19.如图,若,则.
三、解答题
20.在①,②,③这三个条件中选择其中一个,补充在下面的问题中,使命题正确,并证明.
问题:如图,四边形的两条对角线交于点,若 (填序号)
求证:.
21.如图,E是的边BC上的点,已知,,,.求证:.
22.已知如图,D,E分别是的边上的点,.求证:.
23.如图,延长正方形ABCD的一边CB至E,ED与AB相交于点F,过F作FG∥BE交AE于点G,求证:GF=FB.
24.如图:△ABC中,MDAB,MNAE.求证:=.
25.如图,在△ABC中,DF∥AC,DE∥BC.
(1)求证:;
(2)若AE=4,EC=2,BC=10,求BF和CF长.
26.如图,在△ABC中,AB=AC,D为BC边上一点,E为AC边上一点,且∠ADE=∠B.
(1)求证:△ABD∽△DCE;
(2)若AC=12,BC=11,CE=2,求BD的长.
27.如图,在△ABC中,BD平分∠ABC交AC于点D,AD=BD.
(1)求证:△ABC∽△BDC.
(2)若∠C=90°,BC=2,求AB的长.
28.如图,在中,点分别在边上,连接,且.
(1)证明:;
(2)若,当点D在上运动时(点D不与重合),且是等腰三角形,求此时的长.
答案
一、单选题
1.C
【分析】可利用勾股定理求出三角形各边,利用三边对应成比例的两个三角形相似,逐项判定即可.
【详解】解:根据勾股定理,,
∴三边由小到大之比为:
同理,选项A中,用勾股定理求三角形三边由小到大依次为:,三边之比为:,与不满足三边对应成比例,故选项A不符合题意;
同理,选项B中,用勾股定理求三角形三边由小到大依次为:,与不满足三边对应成比例,故选项B不符合题意;
同理,选项C中,用勾股定理求三角形三边由小到大依次为:,三边之比为:,与满足三边对应成比例,故选项C符合题意;
同理,选项D中,用勾股定理求三角形三边由小到大依次为:,,与不满足三边对应成比例,故选项D不符合题意;
故选:C.
2.B
【分析】设小正方形的边长为1,根据已知可求出三边的长,同理可求出阴影部分的各边长,从而根据相似三角形的三边对应成比例即可得到答案.
【详解】解:∵小正方形的边长均为1
∴三边由小到大分别为,2,
同理:A中各边的长分别为:,,3;
B中各边长分别为:1,,;
C中各边长分别为:1、,;
D中各边长分别为:2,,;
由只有B项中的三边与已知三角形的三边对应成比例,且相似比为
故选:B.
3.B
【分析】分别根据网格的特点求得各三角形三边的长,根据三边对应成比例判断两三角形相似即可.
【详解】解:根据网格的特点,①号三角形的三边长分别为:,2,,
②号三角形的三边长分别为:,,3,
③号三角形的三边长分别为:2,,,
④号三角形的三边长分别为:,3,,
,
①与③相似,故B选项正确,符合题意;其他选项不正确
故选:B.
4.A
【分析】利用已知条件得到即,加上对顶角相等,则可判断△AOB∽△COD;再利用比例性质得到,而∠AOC=∠BOD,所以△AOC∽△BOD.
【详解】解:∵OA:OB=OC:OD=2:3,
即,
而∠AOB=∠COD,
∴△AOB∽△COD,
∵,
∴,
∵∠AOC=∠BOD,
∴△AOC∽△BOD.
故选:A.
5.A
【分析】两三角形三条边对应成比例,两三角形相似,据此即可解答.
【详解】解:设每个小正方形的边长为1,则
①△ABC的各边长分别为1、、.
②△ACD的各边长分别为1、、2 ;
③△ADE的各边长分别为2、2 、2 ;
④△AEF的各边长分别为2、2、6;
⑤△AGH的各边长分别为、2、;
∴△ABC∽△AGH,△ADE∽△AGH,
故选A.
6.B
【分析】根据,可以判定,与不一定相等,不能判定PQ//BC.
【详解】解:∵,,
∴,即淇淇的结论正确;
∴,,
∵不能得出或,
∴不能得出PQ//BC,即嘉嘉的结论不正确.
故选B.
7.B
【分析】
根据相似三角形的判定分别进行判断即可得出答案即可.
【详解】解:在三角形纸片ABC中,AB=9,AC=6,BC=12.
A.因为 ,对应边, ,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
B.因为 ,对应边,又∠A=∠A,故沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项正确;
C.因为 ,对应边,即:,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
D、因为 ,对应边, ,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
故选:B.
8.C
【分析】根据相似三角形的判定即可得到结论.
【详解】解:在和中,
∵,
∴只要,
即,
则,
故选:C.
9.D
【分析】根据相似三角形的判定方法,一一判断即可.
【详解】解:∵∠1=∠2,
∴∠DAB=∠BAC,
∴添加∠D=∠B或∠AED=∠C或,可以推出△ADE∽△ABC,
故选:D.
10.C
【分析】本题主要应用两三角形相似的判定定理,三边对应成比例的两个三角形相似,即可完成题目.
【详解】解:①和③相似,
∵由勾股定理求出①的三角形的各边长分别为2、、;
由勾股定理求出③的各边长分别为2、2、2,
∴=,
=,
即==,
∴两三角形的三边对应边成比例,
∴①③相似.
故选:C.
11.A
【分析】求出三组对应边的比,观察是否相等即可作出判断.
【详解】
.
故选:A.
二、填空题
12.
【分析】根据相似三角形的判定方法:两边成比例,夹角相等解题.
【详解】解:根据题意,添加条件,
故答案为:.
13.不相似
【分析】求出,利用,即可求出两个三角形不相似.
【详解】解:∵,,,
∴,
∵,,,
∴,
∴这两个三角形不相似.
故答案为:不相似
14.
【分析】分别求出三个三角形的三边的比(按边长的大小顺序),所求三边之比等于△ABC的三边之比就是与△ABC相似的三角形.
【详解】解:∵△ABC的三边之比是,
△EBC的三边之比是
△CDB的三边之比是,
△DEB的三边之比是.
∴△DEB与△ABC相似,
故答案为:△DEB.
15. 两边的延长线; 相等; 夹角; 成比例.
【分析】根据相似三角形的判定方法直接作答即可.
【详解】(1)平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
(2)两组角对应相等,两三角形相似.
(3)两边对应成比例且夹角相等,两三角形相似.
(4)三边对应成比例,两三角形相似.
故答案为:两边的延长线,相等,夹角,成比例.
16.40°
【分析】由可判定△ABC∽△ADE,得到∠BAC=∠DAE,再根据,,可得出∠DAC的度数.
【详解】解:∵,
∴,
∴,
又∵,
∴.
故答案为:40°.
17.∠AOB=∠DOC
【分析】根据相似三角形的判定,两边对应成比例,夹角相等,两三角形相似解答.
【详解】解:∵,∠AOB=∠DOC,
∴△AOB∽△DOC(两边对应成比例,夹角相等,两三角形相似).
故答案为:∠AOB=∠DOC.
18.
【分析】判断的三边长与哪个三角形的边长对应成比例,即可判定.
【详解】解:的三边长分别为6、8、12,的三边长分别为2、3、2.5
∵
∴与不相似
的三边长分别为6、8、12,的三边长分别为6、3、4
∵
∴与相似
故答案为
19.DE
【分析】结合相似三角形的性质即可求解
【详解】解:
(相似三角形对应边成比例)
故答案是:DE
三、解答题
20.解:选择条件①的证明为:
∵,
∴,
又∵,
∴;
选择条件②的证明为:
∵,
∴.
21.证明:,,
,
,
,
即,
.
22.证明:∵,
又∵,
∴.
23.证明:∵四边形ABCD为正方形,
∴BFCD,
∴=,
∵FGBE,
∴GFAD,
∴=,
∴=,且AD=CD,
∴GF=BF.
24.证明:∵MDAB,
∴=.
∵MNAE,
∴=.
∴==,
即=.
25.(1)证明:∵DF∥AC,
∴,
∵DE∥BC,
∴,
∴;
(2)解:设,
∵,
∴,
∵,且AE=4,EC=2,
∴,
解得:,
∴,
∴.
26.(1)∵AB=AC
∴∠B=∠C
∵∠ADC=∠B+∠BAD
∠ADC=∠ADE+∠CDE
∵∠ADE=∠B
∴∠BAD=∠CDE
∴△ABD∽△CDE
(2)∵AB=AC,AC=12
∴AB=12
由(1)知,△ABD∽△CDE
∴=
即=
∴BD=3或8
27.(1)证明:如图,∵AD=BD,
∴∠A=∠DBA,
∵BD平分∠ABC交AC于点D,
∴∠CBD=∠DBA,
∴∠A=∠CBD,
∵∠C=∠C,
∴△ABC∽△BDC;
(2)解:如图,∵∠C=90°,
∴∠A+∠ABC=90°,
由(1)得
∴∠A =∠ABD=∠CBD,
∴∠A+∠ABD+∠CBD=3∠A=90°,
∴∠A=30°,
∵BC=2,
∴AB=4.
28.解:(1)
如图可知:
在中,
又
.
(2),
是等腰直角三角形
BC=2,AB=AC=BC=
①当AD=AE时,
,
点D在上运动时(点D不与重合),点E在AC上
此情况不符合题意.
②
当AD=DE时,
由(1)结论可知:
AB=DC=
.
③
当AE=DE时,
是等腰直角三角形
,
,即
.
综上所诉:或.
一、单选题
1.如图在正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与相似的三角形所在的网格图形是( )
A. B. C. D.
2.如图,小正方形的边长均为1,则图中三角形(阴影部分)与相似的是( )
A. B. C. D.
3.如图所示,网格中相似的两个三角形是( )
A.①与② B.①与③ C.③与④ D.②与③
4.如图,在四边形ABDC中,不等长的两对角线AD、BC相交于O点,且将四边形ABDC分成甲、乙、丙、丁四个三角形.若OA:OB=OC:OD=2:3,则此四个三角形的关系,下列叙述正确的是( )
A.甲与丙相似,乙与丁相似
B.甲与丙相似,乙与丁不相似
C.甲与丙不相似,乙与丁相似
D.甲与丙不相似,乙与丁不相似
5.如图,在正方形网格中有5个格点三角形,分别是:①,②,③,④,⑤,其中与⑤相似的三角形是( )
A.①③ B.①④ C.②④ D.①③④
6.如图,在中,P、Q分别为AB、AC边上的点,且满足.根据以上信息,嘉嘉和淇淇给出了下列结论:
嘉嘉说:连接PQ,则PQ//BC.
淇淇说:.
对于嘉嘉和淇淇的结论,下列判断正确的是( )
A.嘉嘉正确,淇淇错误 B.嘉嘉错误,淇淇正确
C.两人都正确 D.两人都错误
7.如图,在三角形纸片ABC中,,,,沿虚线剪下的涂色部分的三角形与△ABC相似的是( )
A.B.C.D.
8.如图,已知点D是的边上的一点,根据下列条件,可以得到的是( )
A. B.
C. D.
9.如图,,如果增加一个条件就能使结论成立,那么这个条件可以是( )
A. B. C. D.
10.如图,在大小为的正方形网格中,是相似三角形的是( )
A.①和② B.②和③ C.①和③ D.②和④
11.若△ABC的三边长分别为1,,,△DEF的三边长分别2,,,则与( )
A.一定相似 B.一定不相似
C.不一定相似 D.无法判定是否相似
二、填空题
12.如图,在中,点D,E分别为边,上的点,试添加一个条件: ,使得与相似.(任意写出一个满足条件的即可)
13.在和中,,,,,,判定这两个三角形是否相似 .(填“相似”或“不相似”)
14.如图,在正方形网格中有三个三角形,分别是,,,其中与相似的是 .
15.相似三角形的判定:
(1)平行于三角形一边的直线与其他两边(或 )相交,截得的三角形与原三角形相似.
(2)两组角对应 ,两三角形相似.
(3)两边对应成比例且 相等,两三角形相似.
(4)三边对应 ,两三角形相似.
16.如图,已知,则的度数为 .
17.如图,AC与BD相交于点O,在△AOB和△DOC中,已知,又因为 ,可证明△AOB∽△DOC.
18.的三边长分别为6、8、12,的三边长分别为2、3、2.5,的三边长分别为6、3、4,则与 相似.
19.如图,若,则.
三、解答题
20.在①,②,③这三个条件中选择其中一个,补充在下面的问题中,使命题正确,并证明.
问题:如图,四边形的两条对角线交于点,若 (填序号)
求证:.
21.如图,E是的边BC上的点,已知,,,.求证:.
22.已知如图,D,E分别是的边上的点,.求证:.
23.如图,延长正方形ABCD的一边CB至E,ED与AB相交于点F,过F作FG∥BE交AE于点G,求证:GF=FB.
24.如图:△ABC中,MDAB,MNAE.求证:=.
25.如图,在△ABC中,DF∥AC,DE∥BC.
(1)求证:;
(2)若AE=4,EC=2,BC=10,求BF和CF长.
26.如图,在△ABC中,AB=AC,D为BC边上一点,E为AC边上一点,且∠ADE=∠B.
(1)求证:△ABD∽△DCE;
(2)若AC=12,BC=11,CE=2,求BD的长.
27.如图,在△ABC中,BD平分∠ABC交AC于点D,AD=BD.
(1)求证:△ABC∽△BDC.
(2)若∠C=90°,BC=2,求AB的长.
28.如图,在中,点分别在边上,连接,且.
(1)证明:;
(2)若,当点D在上运动时(点D不与重合),且是等腰三角形,求此时的长.
答案
一、单选题
1.C
【分析】可利用勾股定理求出三角形各边,利用三边对应成比例的两个三角形相似,逐项判定即可.
【详解】解:根据勾股定理,,
∴三边由小到大之比为:
同理,选项A中,用勾股定理求三角形三边由小到大依次为:,三边之比为:,与不满足三边对应成比例,故选项A不符合题意;
同理,选项B中,用勾股定理求三角形三边由小到大依次为:,与不满足三边对应成比例,故选项B不符合题意;
同理,选项C中,用勾股定理求三角形三边由小到大依次为:,三边之比为:,与满足三边对应成比例,故选项C符合题意;
同理,选项D中,用勾股定理求三角形三边由小到大依次为:,,与不满足三边对应成比例,故选项D不符合题意;
故选:C.
2.B
【分析】设小正方形的边长为1,根据已知可求出三边的长,同理可求出阴影部分的各边长,从而根据相似三角形的三边对应成比例即可得到答案.
【详解】解:∵小正方形的边长均为1
∴三边由小到大分别为,2,
同理:A中各边的长分别为:,,3;
B中各边长分别为:1,,;
C中各边长分别为:1、,;
D中各边长分别为:2,,;
由只有B项中的三边与已知三角形的三边对应成比例,且相似比为
故选:B.
3.B
【分析】分别根据网格的特点求得各三角形三边的长,根据三边对应成比例判断两三角形相似即可.
【详解】解:根据网格的特点,①号三角形的三边长分别为:,2,,
②号三角形的三边长分别为:,,3,
③号三角形的三边长分别为:2,,,
④号三角形的三边长分别为:,3,,
,
①与③相似,故B选项正确,符合题意;其他选项不正确
故选:B.
4.A
【分析】利用已知条件得到即,加上对顶角相等,则可判断△AOB∽△COD;再利用比例性质得到,而∠AOC=∠BOD,所以△AOC∽△BOD.
【详解】解:∵OA:OB=OC:OD=2:3,
即,
而∠AOB=∠COD,
∴△AOB∽△COD,
∵,
∴,
∵∠AOC=∠BOD,
∴△AOC∽△BOD.
故选:A.
5.A
【分析】两三角形三条边对应成比例,两三角形相似,据此即可解答.
【详解】解:设每个小正方形的边长为1,则
①△ABC的各边长分别为1、、.
②△ACD的各边长分别为1、、2 ;
③△ADE的各边长分别为2、2 、2 ;
④△AEF的各边长分别为2、2、6;
⑤△AGH的各边长分别为、2、;
∴△ABC∽△AGH,△ADE∽△AGH,
故选A.
6.B
【分析】根据,可以判定,与不一定相等,不能判定PQ//BC.
【详解】解:∵,,
∴,即淇淇的结论正确;
∴,,
∵不能得出或,
∴不能得出PQ//BC,即嘉嘉的结论不正确.
故选B.
7.B
【分析】
根据相似三角形的判定分别进行判断即可得出答案即可.
【详解】解:在三角形纸片ABC中,AB=9,AC=6,BC=12.
A.因为 ,对应边, ,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
B.因为 ,对应边,又∠A=∠A,故沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项正确;
C.因为 ,对应边,即:,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
D、因为 ,对应边, ,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
故选:B.
8.C
【分析】根据相似三角形的判定即可得到结论.
【详解】解:在和中,
∵,
∴只要,
即,
则,
故选:C.
9.D
【分析】根据相似三角形的判定方法,一一判断即可.
【详解】解:∵∠1=∠2,
∴∠DAB=∠BAC,
∴添加∠D=∠B或∠AED=∠C或,可以推出△ADE∽△ABC,
故选:D.
10.C
【分析】本题主要应用两三角形相似的判定定理,三边对应成比例的两个三角形相似,即可完成题目.
【详解】解:①和③相似,
∵由勾股定理求出①的三角形的各边长分别为2、、;
由勾股定理求出③的各边长分别为2、2、2,
∴=,
=,
即==,
∴两三角形的三边对应边成比例,
∴①③相似.
故选:C.
11.A
【分析】求出三组对应边的比,观察是否相等即可作出判断.
【详解】
.
故选:A.
二、填空题
12.
【分析】根据相似三角形的判定方法:两边成比例,夹角相等解题.
【详解】解:根据题意,添加条件,
故答案为:.
13.不相似
【分析】求出,利用,即可求出两个三角形不相似.
【详解】解:∵,,,
∴,
∵,,,
∴,
∴这两个三角形不相似.
故答案为:不相似
14.
【分析】分别求出三个三角形的三边的比(按边长的大小顺序),所求三边之比等于△ABC的三边之比就是与△ABC相似的三角形.
【详解】解:∵△ABC的三边之比是,
△EBC的三边之比是
△CDB的三边之比是,
△DEB的三边之比是.
∴△DEB与△ABC相似,
故答案为:△DEB.
15. 两边的延长线; 相等; 夹角; 成比例.
【分析】根据相似三角形的判定方法直接作答即可.
【详解】(1)平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
(2)两组角对应相等,两三角形相似.
(3)两边对应成比例且夹角相等,两三角形相似.
(4)三边对应成比例,两三角形相似.
故答案为:两边的延长线,相等,夹角,成比例.
16.40°
【分析】由可判定△ABC∽△ADE,得到∠BAC=∠DAE,再根据,,可得出∠DAC的度数.
【详解】解:∵,
∴,
∴,
又∵,
∴.
故答案为:40°.
17.∠AOB=∠DOC
【分析】根据相似三角形的判定,两边对应成比例,夹角相等,两三角形相似解答.
【详解】解:∵,∠AOB=∠DOC,
∴△AOB∽△DOC(两边对应成比例,夹角相等,两三角形相似).
故答案为:∠AOB=∠DOC.
18.
【分析】判断的三边长与哪个三角形的边长对应成比例,即可判定.
【详解】解:的三边长分别为6、8、12,的三边长分别为2、3、2.5
∵
∴与不相似
的三边长分别为6、8、12,的三边长分别为6、3、4
∵
∴与相似
故答案为
19.DE
【分析】结合相似三角形的性质即可求解
【详解】解:
(相似三角形对应边成比例)
故答案是:DE
三、解答题
20.解:选择条件①的证明为:
∵,
∴,
又∵,
∴;
选择条件②的证明为:
∵,
∴.
21.证明:,,
,
,
,
即,
.
22.证明:∵,
又∵,
∴.
23.证明:∵四边形ABCD为正方形,
∴BFCD,
∴=,
∵FGBE,
∴GFAD,
∴=,
∴=,且AD=CD,
∴GF=BF.
24.证明:∵MDAB,
∴=.
∵MNAE,
∴=.
∴==,
即=.
25.(1)证明:∵DF∥AC,
∴,
∵DE∥BC,
∴,
∴;
(2)解:设,
∵,
∴,
∵,且AE=4,EC=2,
∴,
解得:,
∴,
∴.
26.(1)∵AB=AC
∴∠B=∠C
∵∠ADC=∠B+∠BAD
∠ADC=∠ADE+∠CDE
∵∠ADE=∠B
∴∠BAD=∠CDE
∴△ABD∽△CDE
(2)∵AB=AC,AC=12
∴AB=12
由(1)知,△ABD∽△CDE
∴=
即=
∴BD=3或8
27.(1)证明:如图,∵AD=BD,
∴∠A=∠DBA,
∵BD平分∠ABC交AC于点D,
∴∠CBD=∠DBA,
∴∠A=∠CBD,
∵∠C=∠C,
∴△ABC∽△BDC;
(2)解:如图,∵∠C=90°,
∴∠A+∠ABC=90°,
由(1)得
∴∠A =∠ABD=∠CBD,
∴∠A+∠ABD+∠CBD=3∠A=90°,
∴∠A=30°,
∵BC=2,
∴AB=4.
28.解:(1)
如图可知:
在中,
又
.
(2),
是等腰直角三角形
BC=2,AB=AC=BC=
①当AD=AE时,
,
点D在上运动时(点D不与重合),点E在AC上
此情况不符合题意.
②
当AD=DE时,
由(1)结论可知:
AB=DC=
.
③
当AE=DE时,
是等腰直角三角形
,
,即
.
综上所诉:或.
