人教版数学九年级下册《反比例函数》中考复习课件(共24张PPT)
文档属性
| 名称 | 人教版数学九年级下册《反比例函数》中考复习课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-06 10:33:42 | ||
图片预览








文档简介
(共24张PPT)
中考复习
反比例函数
01
知识梳理
·知识点1 反比例函数的有关概念
·知识点2 反比例函数的图象与性质
·知识点3 反比例函数解析式的求法
·知识点4 反比例函数的实际应用
知识点1 反比例函数的有关概念
k·x-1
定义
解析式的 三种形式
例:下列哪些关系式中的y 是χ的反比例函数?
①y=4χ ② =3 ③y=χ +1 ④χy=5
⑤ y=4χ-1 ⑥y=- ⑦y=
④ ⑤ ⑥
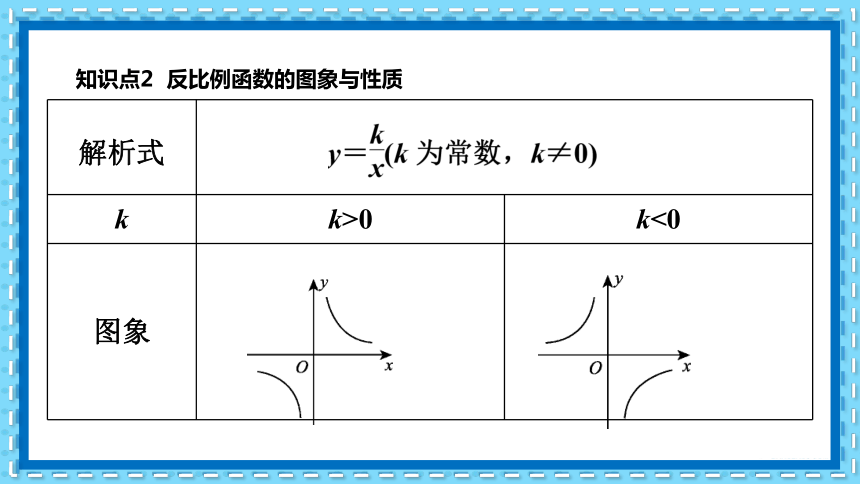
解析式 k k>0 k<0
图象
知识点2 反比例函数的图象与性质
所在象限 第③________象限(x,y同号) 第⑤________象限(x,y异号)
性质 在每个象限内,y随x的增大而④________ 在每个象限内,y随x的增大而⑥________
对称性 一、三
减小
二、四
增大
既是中心对称图形又是轴对称图形
例1.如果反比例函数y= (a是常数)的图象在第一、三象限,那么a的取值范围是 ( )
A.a<0 B.a>0 C.a<2 D.a>2
D
例2.函数y=kx-3与y= (k≠0)在同一坐标系内的图象可能是( )
答案 B ∵当k>0时,y=kx-3的图象过第一、三、四象限,反比例函数y= 的图象过第一、三象限,当
k<0时,y=kx-3的图象过第二、三、四象限,反比例函数y= 的图象过第二、四象限,
∴B正确,故选B.
B
知识点3 反比例函数解析式的求法
待定系 数法
ab
例:已知正比例函数y= 2x的图象与反比例函数y= 的图象有一个交点的纵坐标是2,求反比例函数的解析式。
解: 根据题意得: 2=2x
∴x= 1
则交点坐标(1, 2)
∴k=2×1=2
∴反比例函数的解析式为 y=
2
x
知识点4 反比例函数的实际应用
例:一辆汽车从甲地开往乙地,随着汽车的平均速度v(km / h)的变化,所需时间t(h)的变化情况如图所示.
(1)甲、乙两地相距多少千米
(2)写出t关于v的函数解析式;
(3)当汽车的平均速度为75km / h时,
所需时间为多少
(1)600km
(2)t=
600
v
(v>0)
(3)8h
考点突破
02
例:若点A(-3,y1)B(-2,y2)C(1,y3)都在反比例函数y= - 的图象上,则y1,y2,y3的大小关系( )
A. y2< y1 < y3 B. y3< y1 < y2
C. y1< y2 < y3 D. y3< y2考点1 反比例函数的图象与性质
B
例:如图,一次函数y= -x+3的图象与反比例函数y= (k≠0)在第一象限内的图象交于A(1,a)和B两点,与x轴交于点C.
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△APC的面积为5,求点P的坐标.
考点2 反比例函数的综合应用
解析 (1)把点A(1,a)代入y=-x+3中,得a=2.
∴A(1,2)
把A(1,2)代入反比例函数y= 中,
得k=1×2=2,
∴反比例函数的表达式为y= .
(2)∵一次函数y=-x+3的图象与x轴交于点C,
∴C(3,0),
设P(x,0),∴PC=|3-x|,
∴S△APC= |3-x|×2=5,
解得x=-2或x=8,
∴P点的坐标为(-2,0)或(8,0).
解题关键 本题考查了反比例函数图象与一次函数图象的交点问题,求出反比例函数的解析式是解此
题的关键.
03
中考聚焦
1.反比例函数y= 的图象经过点(2,1),则下列说法错误的是 ( )
A.k=2
B.函数图象分布在第一、三象限
C.当x>0时,y随x的增大而增大
D.当x>0时,y随x的增大而减小
将点(2,1)代入y= 中,解得k=2.
A.k=2,说法正确;
B.k=2>0,反比例函数图象分布在第一、三象限,说法正确;
C.k=2>0,当x>0时,函数图象位于第一象限,且y随x的增大而减小,说法错误;
D.k=2>0,当x>0时,函数图象位于第一象限,且y随x的增大而减小,说法正确.
故选C.
C
2. 如图所示,小英同学根据学习函数的经验,自主尝试在平面直角坐标系中画出了一个解析式为 = 的函数图象.根据这个函数的图象,下列说法正确的是( )
A. 图象与x轴没有交点
B. 当 时
C. 图象与y轴的交点是
D. 随 的增大而减小
A
3.在同一平面直角坐标系中,一次函数y1=k1x+b与反比例函数
y2= (x>0)的图象如图所示,则当y1>y2时,自变量x的取值范围为 ( )
A.x<1 B.x>3 C.0答案 D 由图象可得一次函数y1=k1x+b与反比例函数y2= (x>0)的图象的两个交点的横坐标分别是1,3,所以当y1>y2时,x的取值范围为1D
小结与作业
小结:1、反比例函数解析式有哪几种形式?
2、求反比例函数解析式的方法是什么?
3、回顾反比例函数的图像与性质。
作业:
1、已知点A(n,m)在反比例函数y= 的图象上,若n>2,则m的取值范围为 。
2、 反比例函数y= (k 为常数,且 )的图象经过点
A(1,3)、B(3,m)。
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P,使PA+PB的值最
小,求满足条件的点P的坐标。
中考复习
反比例函数
01
知识梳理
·知识点1 反比例函数的有关概念
·知识点2 反比例函数的图象与性质
·知识点3 反比例函数解析式的求法
·知识点4 反比例函数的实际应用
知识点1 反比例函数的有关概念
k·x-1
定义
解析式的 三种形式
例:下列哪些关系式中的y 是χ的反比例函数?
①y=4χ ② =3 ③y=χ +1 ④χy=5
⑤ y=4χ-1 ⑥y=- ⑦y=
④ ⑤ ⑥
解析式 k k>0 k<0
图象
知识点2 反比例函数的图象与性质
所在象限 第③________象限(x,y同号) 第⑤________象限(x,y异号)
性质 在每个象限内,y随x的增大而④________ 在每个象限内,y随x的增大而⑥________
对称性 一、三
减小
二、四
增大
既是中心对称图形又是轴对称图形
例1.如果反比例函数y= (a是常数)的图象在第一、三象限,那么a的取值范围是 ( )
A.a<0 B.a>0 C.a<2 D.a>2
D
例2.函数y=kx-3与y= (k≠0)在同一坐标系内的图象可能是( )
答案 B ∵当k>0时,y=kx-3的图象过第一、三、四象限,反比例函数y= 的图象过第一、三象限,当
k<0时,y=kx-3的图象过第二、三、四象限,反比例函数y= 的图象过第二、四象限,
∴B正确,故选B.
B
知识点3 反比例函数解析式的求法
待定系 数法
ab
例:已知正比例函数y= 2x的图象与反比例函数y= 的图象有一个交点的纵坐标是2,求反比例函数的解析式。
解: 根据题意得: 2=2x
∴x= 1
则交点坐标(1, 2)
∴k=2×1=2
∴反比例函数的解析式为 y=
2
x
知识点4 反比例函数的实际应用
例:一辆汽车从甲地开往乙地,随着汽车的平均速度v(km / h)的变化,所需时间t(h)的变化情况如图所示.
(1)甲、乙两地相距多少千米
(2)写出t关于v的函数解析式;
(3)当汽车的平均速度为75km / h时,
所需时间为多少
(1)600km
(2)t=
600
v
(v>0)
(3)8h
考点突破
02
例:若点A(-3,y1)B(-2,y2)C(1,y3)都在反比例函数y= - 的图象上,则y1,y2,y3的大小关系( )
A. y2< y1 < y3 B. y3< y1 < y2
C. y1< y2 < y3 D. y3< y2
B
例:如图,一次函数y= -x+3的图象与反比例函数y= (k≠0)在第一象限内的图象交于A(1,a)和B两点,与x轴交于点C.
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△APC的面积为5,求点P的坐标.
考点2 反比例函数的综合应用
解析 (1)把点A(1,a)代入y=-x+3中,得a=2.
∴A(1,2)
把A(1,2)代入反比例函数y= 中,
得k=1×2=2,
∴反比例函数的表达式为y= .
(2)∵一次函数y=-x+3的图象与x轴交于点C,
∴C(3,0),
设P(x,0),∴PC=|3-x|,
∴S△APC= |3-x|×2=5,
解得x=-2或x=8,
∴P点的坐标为(-2,0)或(8,0).
解题关键 本题考查了反比例函数图象与一次函数图象的交点问题,求出反比例函数的解析式是解此
题的关键.
03
中考聚焦
1.反比例函数y= 的图象经过点(2,1),则下列说法错误的是 ( )
A.k=2
B.函数图象分布在第一、三象限
C.当x>0时,y随x的增大而增大
D.当x>0时,y随x的增大而减小
将点(2,1)代入y= 中,解得k=2.
A.k=2,说法正确;
B.k=2>0,反比例函数图象分布在第一、三象限,说法正确;
C.k=2>0,当x>0时,函数图象位于第一象限,且y随x的增大而减小,说法错误;
D.k=2>0,当x>0时,函数图象位于第一象限,且y随x的增大而减小,说法正确.
故选C.
C
2. 如图所示,小英同学根据学习函数的经验,自主尝试在平面直角坐标系中画出了一个解析式为 = 的函数图象.根据这个函数的图象,下列说法正确的是( )
A. 图象与x轴没有交点
B. 当 时
C. 图象与y轴的交点是
D. 随 的增大而减小
A
3.在同一平面直角坐标系中,一次函数y1=k1x+b与反比例函数
y2= (x>0)的图象如图所示,则当y1>y2时,自变量x的取值范围为 ( )
A.x<1 B.x>3 C.0
小结与作业
小结:1、反比例函数解析式有哪几种形式?
2、求反比例函数解析式的方法是什么?
3、回顾反比例函数的图像与性质。
作业:
1、已知点A(n,m)在反比例函数y= 的图象上,若n>2,则m的取值范围为 。
2、 反比例函数y= (k 为常数,且 )的图象经过点
A(1,3)、B(3,m)。
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P,使PA+PB的值最
小,求满足条件的点P的坐标。
