北师大版数学八年级下册3.2图形的旋转课件(共15张PPT)
文档属性
| 名称 | 北师大版数学八年级下册3.2图形的旋转课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-06 10:53:46 | ||
图片预览




文档简介
(共15张PPT)
图形的旋转
一.创设情境,引入概念
展示图片:在我们的周围存在着很多转动 着的物体,请同学们欣赏。
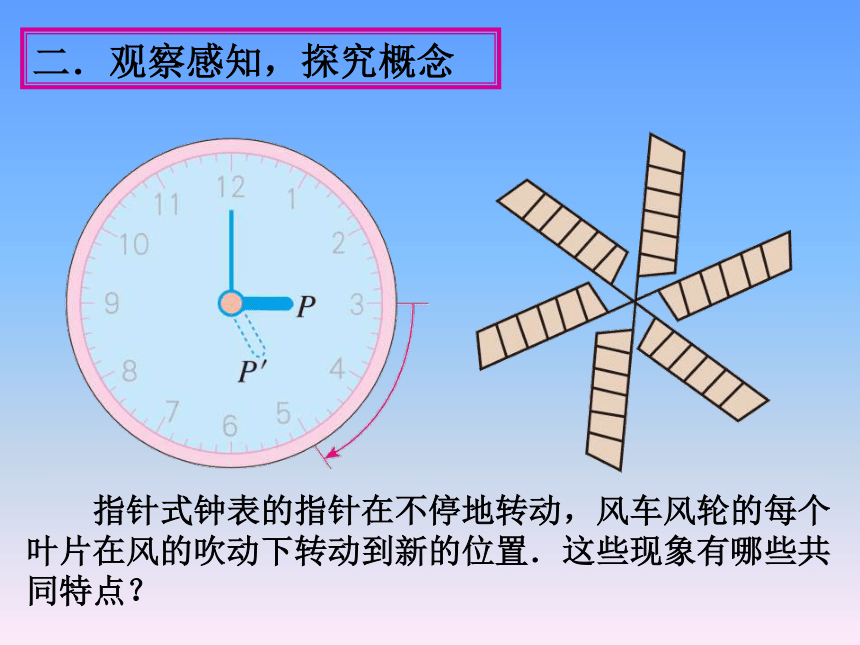
二.观察感知,探究概念
指针式钟表的指针在不停地转动,风车风轮的每个
叶片在风的吹动下转动到新的位置.这些现象有哪些共
同特点?
O
P′
P
定义
120°
把一个平面图形绕着平面内某一点 O 转动一个角度的图形变换叫做图形的旋转.这个点 O 叫旋转中心,转动的角叫做旋转角.
如果图形上的点 P 经过旋转变为点 P′,那么这两个点叫做这个旋转的对应点.
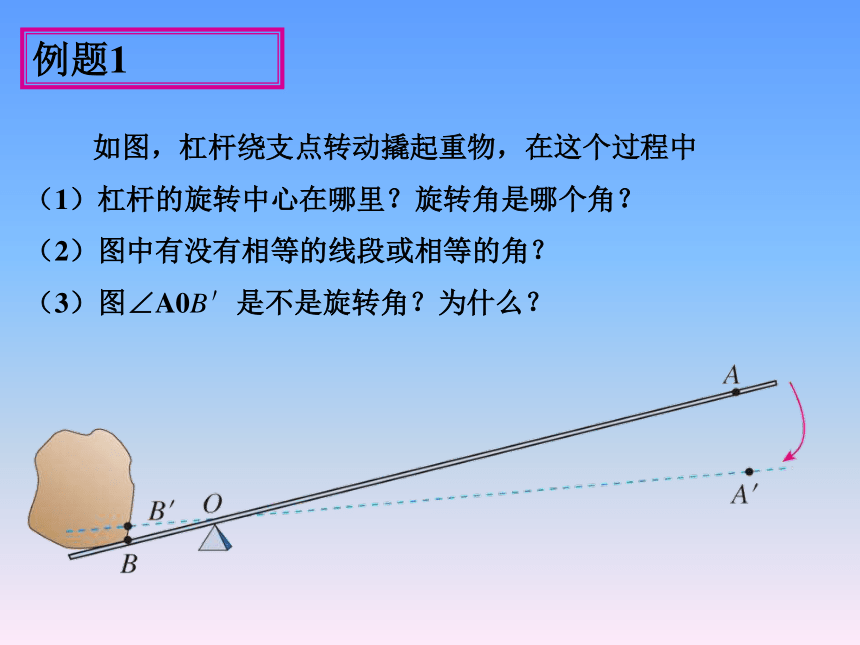
如图,杠杆绕支点转动撬起重物,在这个过程中
(1)杠杆的旋转中心在哪里?旋转角是哪个角?
(2)图中有没有相等的线段或相等的角?
(3)图∠A0B'是不是旋转角?为什么?
例题1
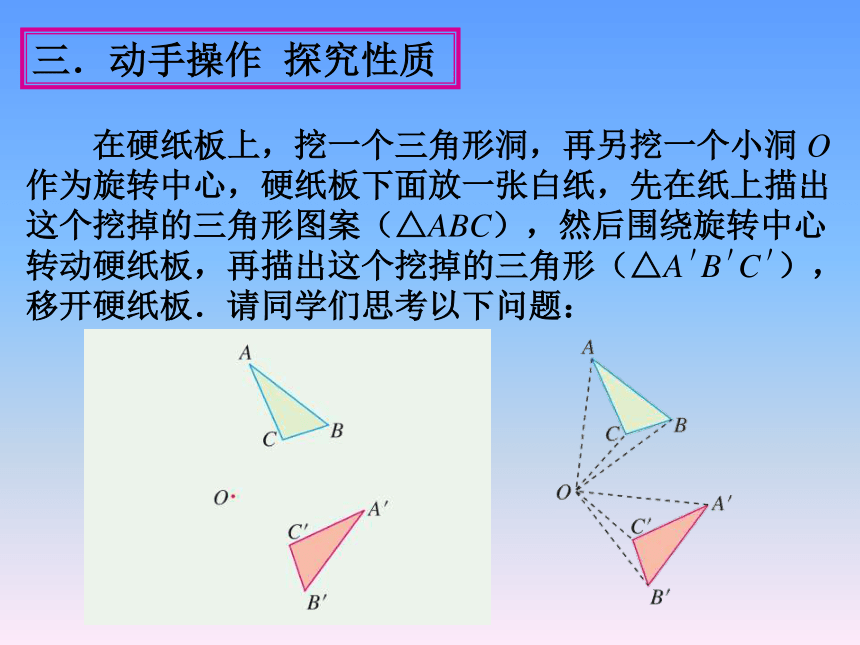
在硬纸板上,挖一个三角形洞,再另挖一个小洞 O
作为旋转中心,硬纸板下面放一张白纸,先在纸上描出
这个挖掉的三角形图案(△ABC),然后围绕旋转中心
转动硬纸板,再描出这个挖掉的三角形(△A B C ),
移开硬纸板.请同学们思考以下问题:
'
'
'
三.动手操作 探究性质
三.动手操作 探究性质
(1)△A B C 可以
看作 △ABC 经过怎样的运
动得到的?
'
'
'
(2)线段 OA 和 OA' 有什么关系?∠AOA'和∠BOB'有什么关系?
(3)你还能发现哪些
有类似关系的线段和角?
'
'
'
(4)△ABC和△A B C
的形状和大小有什么关系?
(5)你能把以上发现,用自己的语言归纳概括一下吗?
◆ 对应点到旋转中心的距离相等.
◆ 对应点与旋转中心所连线段的夹角等于旋转角.
◆ 旋转前、后的图形全等.
旋转的性质
三.动手操作 探究性质
怎样验证你的猜想的正确性?
例1 如图, E 是正方形 ABCD 中 CD 边上任意一
点,以点 A 为中心,把 △ADE 顺时针旋转 90°,你能
画出旋转后的图形吗?试一试你有几种方法?
四.问题解决 应用新知
A
B
C
E
D
方法1:
F
图中 △ABF 为所求图形.
A
B
C
E
D
四.问题解决 应用新知
方法2:
F
图中 △ABF 为所求图形.
A
B
C
E
D
四.问题解决 应用新知
方法3:
F
图中 △ABF 为所求图形.
A
B
C
E
D
四.问题解决 应用新知
请你在生活中再找找属于旋转的图形,并试着画一画。
五.布置作业
谢谢观看
图形的旋转
一.创设情境,引入概念
展示图片:在我们的周围存在着很多转动 着的物体,请同学们欣赏。
二.观察感知,探究概念
指针式钟表的指针在不停地转动,风车风轮的每个
叶片在风的吹动下转动到新的位置.这些现象有哪些共
同特点?
O
P′
P
定义
120°
把一个平面图形绕着平面内某一点 O 转动一个角度的图形变换叫做图形的旋转.这个点 O 叫旋转中心,转动的角叫做旋转角.
如果图形上的点 P 经过旋转变为点 P′,那么这两个点叫做这个旋转的对应点.
如图,杠杆绕支点转动撬起重物,在这个过程中
(1)杠杆的旋转中心在哪里?旋转角是哪个角?
(2)图中有没有相等的线段或相等的角?
(3)图∠A0B'是不是旋转角?为什么?
例题1
在硬纸板上,挖一个三角形洞,再另挖一个小洞 O
作为旋转中心,硬纸板下面放一张白纸,先在纸上描出
这个挖掉的三角形图案(△ABC),然后围绕旋转中心
转动硬纸板,再描出这个挖掉的三角形(△A B C ),
移开硬纸板.请同学们思考以下问题:
'
'
'
三.动手操作 探究性质
三.动手操作 探究性质
(1)△A B C 可以
看作 △ABC 经过怎样的运
动得到的?
'
'
'
(2)线段 OA 和 OA' 有什么关系?∠AOA'和∠BOB'有什么关系?
(3)你还能发现哪些
有类似关系的线段和角?
'
'
'
(4)△ABC和△A B C
的形状和大小有什么关系?
(5)你能把以上发现,用自己的语言归纳概括一下吗?
◆ 对应点到旋转中心的距离相等.
◆ 对应点与旋转中心所连线段的夹角等于旋转角.
◆ 旋转前、后的图形全等.
旋转的性质
三.动手操作 探究性质
怎样验证你的猜想的正确性?
例1 如图, E 是正方形 ABCD 中 CD 边上任意一
点,以点 A 为中心,把 △ADE 顺时针旋转 90°,你能
画出旋转后的图形吗?试一试你有几种方法?
四.问题解决 应用新知
A
B
C
E
D
方法1:
F
图中 △ABF 为所求图形.
A
B
C
E
D
四.问题解决 应用新知
方法2:
F
图中 △ABF 为所求图形.
A
B
C
E
D
四.问题解决 应用新知
方法3:
F
图中 △ABF 为所求图形.
A
B
C
E
D
四.问题解决 应用新知
请你在生活中再找找属于旋转的图形,并试着画一画。
五.布置作业
谢谢观看
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
