人教版数学七年级下册7.1.1 两条直线相交 (含解析)
文档属性
| 名称 | 人教版数学七年级下册7.1.1 两条直线相交 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 798.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-05 21:43:11 | ||
图片预览




文档简介
7.1.1 两条直线相交
一、单选题
1.下列图中,和是对顶角的有( )个.
A.个 B.个 C.个 D.个
2.按语句画图:点在直线上,也在直线上,但不在直线上,直线,,两两相交正确的是( )
A.B.C.D.
3.如图,直线,相交于点,平分,若,则的度数为( )
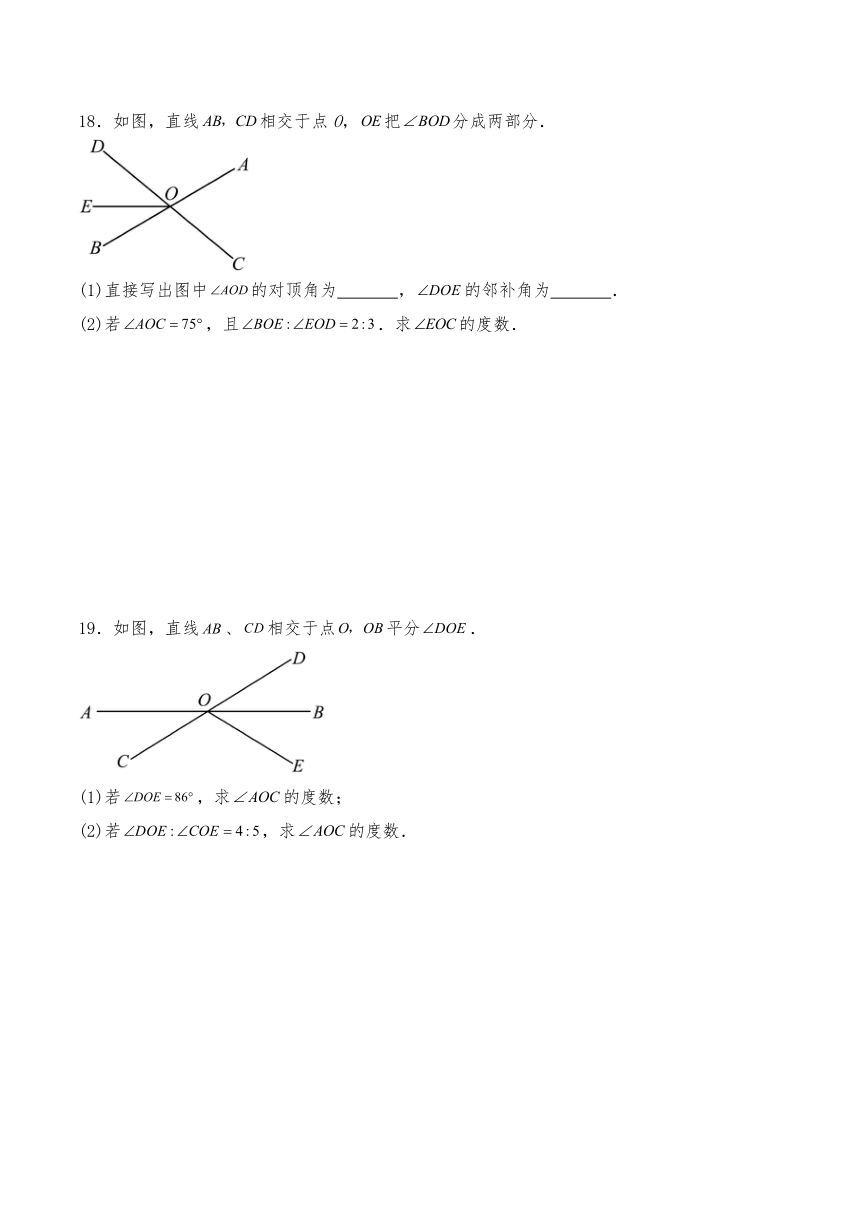
A. B. C. D.
4.如图,直线,,相交于点,,,则( )
A. B. C. D.
5.已知与互为对顶角,与互余,若,则的度数是( )
A. B. C. D.或
6.如图,直线, 相交于点O,已知,射线把分成两部分,且,则的度数为( )
A. B. C. D.
7.如图,直线AB,AB相交于点O,OE,OF为射线,则对顶角有( )
A.1对 B.2对 C.3对 D.4对
二、填空题
8.三条直线AB、CD、EF相交于点O,如图所示,∠AOD的对顶角是 ,∠FOB的对顶角是 ,∠EOB的邻补角是
9.如图,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数,那么这个破损扇形零件的圆心角的度数是 °.
10.如图,直线与相交于点,则的度数是 .
11.如图,直线,相交于点O,平分,若,则 .
12.若的对顶角是,的邻补角是,的余角是,若,则 .
13.如图,过直线AB上一点O作射线OC,∠BOC=29°38′,OD平分∠AOC,则∠DOC的度数为 .
14.如图,直线交于点O,,若,则 °.
三、解答题
15.如图,直线和直线相交于点,平分.
(1)写出图中的对顶角______,和两个邻补角______;
(2)若,求的度数.
16.如图,直线,相交于点,平分.
(1)若,求的度数;
(2)若,求的度数.
17.如图,直线、相交于点O,平分,平分,.
(1)求的度数;
(2)求的度数.
18.如图,直线相交于点O,把分成两部分.
(1)直接写出图中的对顶角为 ,的邻补角为 .
(2)若,且.求的度数.
19.如图,直线、相交于点平分.
(1)若,求的度数;
(2)若,求的度数.
20.如图,直线AC,EF相交于点O,OD是的平分线,OE在内,,,求的度数.
21.已知直线经过点O,,射线是的角平分线.
(1)如图1,若,求的度数;
(2)将图1中的绕顶点O逆时针旋转到图2的位置,若,求的度数;
(3)若度,由(1),(2)猜测大小,请你直接写出________度;(用含x的式子表示)
答案
一、单选题
1.A
【分析】根据对顶角的两边互为反向延长线对各图形分析判断后进行解答.
【详解】根据对顶角的定义:
中和不是对顶角;
中和是对顶角;
中和不是对顶角;
中和不是对顶角;
故选:.
2.A
【分析】根据相交线的概念、点与直线的位置关系进行判断即可.
【详解】解:A.符合条件,
B.不符合点P不在直线c上;
C.不符合点P在直线a上;
D.不符合直线a、b、c两两相交;
故选:A.
3.D
【分析】首先根据对顶角相等和角平分线的概念得到,然后根据平角的概念求解即可.
【详解】∵
∴
∵平分,
∴
∴.
故选:D.
4.D
【分析】先求得的对顶角的度数,结合平角的性质即可求得答案.
【详解】如图所示.
∵与为对顶角,
∴.
∴.
故选:D.
5.A
【分析】根据对顶角的性质以及互余的定义即可求出答案.
【详解】解:由题意可知:,
,,
,
,
.
故选:.
6.B
【分析】根据对顶角相等求出的度数,再根据,即可求出的度数.
【详解】解:,
,
,
,
故选:B.
7.B
【分析】根据对顶角的定义,对顶角的两边互为反向延长线,可以判断.
【详解】图中对顶角有:∠AOC与∠BOD、∠AOD与∠BOC,共2对.
故选B.
二、填空题
8. ∠BOC ∠AOE ∠AOE和∠BOF
【分析】根据对顶角和邻补角的定义解答,注意两直线相交,一个角的对顶角只有一个,但邻补角有两个.
【详解】对顶角和邻补角在两条直线相交的上形中产生,根据对顶角、邻补角的定义得:
∠AOD的对顶角是∠BOC,
∠FOB的对顶角是∠AOE,
∠EOB的邻补角是∠AOE和∠BOF.
故答案为(1)∠BOC (2)∠AOE (3)∠AOE和∠BOF
9.
【分析】由题意知,一个破损的扇形零件的圆心角与其两边的反向延长线组的角是对顶角,根据对顶角的性质解答即可.
【详解】解:由题意得,扇形零件的圆心角与其两边的反向延长线组的角是对顶角,
图中的量角器显示的度数是,
∴扇形零件的圆心角;
故答案为:.
10.
【分析】由对顶角相等列出方程求得,然后根据邻补角的性质求得即可.
【详解】解:由对顶角相等可知:∠AOC=∠BOD,
∴,
解得:,
∴,
∵,
∴.
故答案为:.
11.
【分析】利用角平分线的定义和对顶角的性质,得到,进而得到,再利用邻补角互补,即可求出的度数.
【详解】解:平分,
,
,
,
,
,
,
,
,
,
故答案为:.
12.145
【分析】根据余角、邻补角、对顶角的性质进行求解,即可得到答案.
【详解】解:的余角是,,
,
的邻补角是,
,
的对顶角是,
,
故答案为:145.
13.
【分析】先根据邻补角互补求出∠AOC=150°22′,再由角平分线的定义求解即可.
【详解】解:∵∠BOC=29°38′,∠AOC+∠BOC=180°,
∴∠AOC=150°22′,
∵OD平分∠AOC,
∴,
故答案为:.
14.96
【分析】对顶角相等,得到,根据,求出的度数,进而求出的度数,互补关系,求出即可.
【详解】解:∵
∴,
∵,
∴,
∴,
∴;
故答案为:96.
三、解答题
15.(1)解:的对顶角是,
∵,
∴的邻补角是,
故答案为:,.
(2)解:∵,平分,
∴,
∴,
∵,
∴,
∴的度数为.
16.(1)解:∵,
∴,
平分,
∴,
∴;
(2)解:,,
,,
平分,
,
,
∴的度数为.
17.(1)解:∵,,
∴,
∵平分,
∴;
(2)∵,
∴,
∵平分,
∴,
∴.
18.(1)解:由题意可得:的对顶角为,的邻补角为
故答案为:,
(2)由可得,,则
∵
∴
∴.
19.(1)解:∵,平分,
∴,
∴;
(2)解:∵,
设,则.
∵,
∴,解得,
∴,,
∴.
20.解:,
是的平分线,
,
,
即,
.
.
21.(1)∵,
∴.
∵是的角平分线,
∴,
∵,
∴;
(2)∵,,
∴,
∵是的角平分线,
∴,
∴;
(3)∵,,
∴,
∵是的角平分线,
∴,
∴.
故答案为:.
一、单选题
1.下列图中,和是对顶角的有( )个.
A.个 B.个 C.个 D.个
2.按语句画图:点在直线上,也在直线上,但不在直线上,直线,,两两相交正确的是( )
A.B.C.D.
3.如图,直线,相交于点,平分,若,则的度数为( )
A. B. C. D.
4.如图,直线,,相交于点,,,则( )
A. B. C. D.
5.已知与互为对顶角,与互余,若,则的度数是( )
A. B. C. D.或
6.如图,直线, 相交于点O,已知,射线把分成两部分,且,则的度数为( )
A. B. C. D.
7.如图,直线AB,AB相交于点O,OE,OF为射线,则对顶角有( )
A.1对 B.2对 C.3对 D.4对
二、填空题
8.三条直线AB、CD、EF相交于点O,如图所示,∠AOD的对顶角是 ,∠FOB的对顶角是 ,∠EOB的邻补角是
9.如图,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数,那么这个破损扇形零件的圆心角的度数是 °.
10.如图,直线与相交于点,则的度数是 .
11.如图,直线,相交于点O,平分,若,则 .
12.若的对顶角是,的邻补角是,的余角是,若,则 .
13.如图,过直线AB上一点O作射线OC,∠BOC=29°38′,OD平分∠AOC,则∠DOC的度数为 .
14.如图,直线交于点O,,若,则 °.
三、解答题
15.如图,直线和直线相交于点,平分.
(1)写出图中的对顶角______,和两个邻补角______;
(2)若,求的度数.
16.如图,直线,相交于点,平分.
(1)若,求的度数;
(2)若,求的度数.
17.如图,直线、相交于点O,平分,平分,.
(1)求的度数;
(2)求的度数.
18.如图,直线相交于点O,把分成两部分.
(1)直接写出图中的对顶角为 ,的邻补角为 .
(2)若,且.求的度数.
19.如图,直线、相交于点平分.
(1)若,求的度数;
(2)若,求的度数.
20.如图,直线AC,EF相交于点O,OD是的平分线,OE在内,,,求的度数.
21.已知直线经过点O,,射线是的角平分线.
(1)如图1,若,求的度数;
(2)将图1中的绕顶点O逆时针旋转到图2的位置,若,求的度数;
(3)若度,由(1),(2)猜测大小,请你直接写出________度;(用含x的式子表示)
答案
一、单选题
1.A
【分析】根据对顶角的两边互为反向延长线对各图形分析判断后进行解答.
【详解】根据对顶角的定义:
中和不是对顶角;
中和是对顶角;
中和不是对顶角;
中和不是对顶角;
故选:.
2.A
【分析】根据相交线的概念、点与直线的位置关系进行判断即可.
【详解】解:A.符合条件,
B.不符合点P不在直线c上;
C.不符合点P在直线a上;
D.不符合直线a、b、c两两相交;
故选:A.
3.D
【分析】首先根据对顶角相等和角平分线的概念得到,然后根据平角的概念求解即可.
【详解】∵
∴
∵平分,
∴
∴.
故选:D.
4.D
【分析】先求得的对顶角的度数,结合平角的性质即可求得答案.
【详解】如图所示.
∵与为对顶角,
∴.
∴.
故选:D.
5.A
【分析】根据对顶角的性质以及互余的定义即可求出答案.
【详解】解:由题意可知:,
,,
,
,
.
故选:.
6.B
【分析】根据对顶角相等求出的度数,再根据,即可求出的度数.
【详解】解:,
,
,
,
故选:B.
7.B
【分析】根据对顶角的定义,对顶角的两边互为反向延长线,可以判断.
【详解】图中对顶角有:∠AOC与∠BOD、∠AOD与∠BOC,共2对.
故选B.
二、填空题
8. ∠BOC ∠AOE ∠AOE和∠BOF
【分析】根据对顶角和邻补角的定义解答,注意两直线相交,一个角的对顶角只有一个,但邻补角有两个.
【详解】对顶角和邻补角在两条直线相交的上形中产生,根据对顶角、邻补角的定义得:
∠AOD的对顶角是∠BOC,
∠FOB的对顶角是∠AOE,
∠EOB的邻补角是∠AOE和∠BOF.
故答案为(1)∠BOC (2)∠AOE (3)∠AOE和∠BOF
9.
【分析】由题意知,一个破损的扇形零件的圆心角与其两边的反向延长线组的角是对顶角,根据对顶角的性质解答即可.
【详解】解:由题意得,扇形零件的圆心角与其两边的反向延长线组的角是对顶角,
图中的量角器显示的度数是,
∴扇形零件的圆心角;
故答案为:.
10.
【分析】由对顶角相等列出方程求得,然后根据邻补角的性质求得即可.
【详解】解:由对顶角相等可知:∠AOC=∠BOD,
∴,
解得:,
∴,
∵,
∴.
故答案为:.
11.
【分析】利用角平分线的定义和对顶角的性质,得到,进而得到,再利用邻补角互补,即可求出的度数.
【详解】解:平分,
,
,
,
,
,
,
,
,
,
故答案为:.
12.145
【分析】根据余角、邻补角、对顶角的性质进行求解,即可得到答案.
【详解】解:的余角是,,
,
的邻补角是,
,
的对顶角是,
,
故答案为:145.
13.
【分析】先根据邻补角互补求出∠AOC=150°22′,再由角平分线的定义求解即可.
【详解】解:∵∠BOC=29°38′,∠AOC+∠BOC=180°,
∴∠AOC=150°22′,
∵OD平分∠AOC,
∴,
故答案为:.
14.96
【分析】对顶角相等,得到,根据,求出的度数,进而求出的度数,互补关系,求出即可.
【详解】解:∵
∴,
∵,
∴,
∴,
∴;
故答案为:96.
三、解答题
15.(1)解:的对顶角是,
∵,
∴的邻补角是,
故答案为:,.
(2)解:∵,平分,
∴,
∴,
∵,
∴,
∴的度数为.
16.(1)解:∵,
∴,
平分,
∴,
∴;
(2)解:,,
,,
平分,
,
,
∴的度数为.
17.(1)解:∵,,
∴,
∵平分,
∴;
(2)∵,
∴,
∵平分,
∴,
∴.
18.(1)解:由题意可得:的对顶角为,的邻补角为
故答案为:,
(2)由可得,,则
∵
∴
∴.
19.(1)解:∵,平分,
∴,
∴;
(2)解:∵,
设,则.
∵,
∴,解得,
∴,,
∴.
20.解:,
是的平分线,
,
,
即,
.
.
21.(1)∵,
∴.
∵是的角平分线,
∴,
∵,
∴;
(2)∵,,
∴,
∵是的角平分线,
∴,
∴;
(3)∵,,
∴,
∵是的角平分线,
∴,
∴.
故答案为:.
同课章节目录
