人教版数学七年级下册7.2.2平行线的判定(含解析)
文档属性
| 名称 | 人教版数学七年级下册7.2.2平行线的判定(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 858.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-05 21:45:55 | ||
图片预览



文档简介
7.2.2 平行线的判定
一、单选题
1.在同一平面内,是直线,下列关于它们位置关系的说法中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.如图,已知直线外一点,过点画直线,使,借助三角板有如下操作:
①固定直尺,并沿方向移动三角板,使斜边经过点;
②用三角板的斜边靠上直线;
③沿三角板斜边画直线;
④用直尺紧靠三角板的一条直角边.
正确的操作顺序是( )
A.①②③④ B.②④③① C.②④①③ D.④③②①
3.一学员练习驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,则这两次拐弯的角度可能是( )
A.第一次向左拐,第二次向右拐
B.第一次向右拐,第二次向左拐
C.第一次向右拐,第二次向右拐
D.第一次向左拐,第二次向左拐
4.如图,在中,点D,E,F分别在边,,上,则下列条件中,能判定的是( )
A. B. C. D.
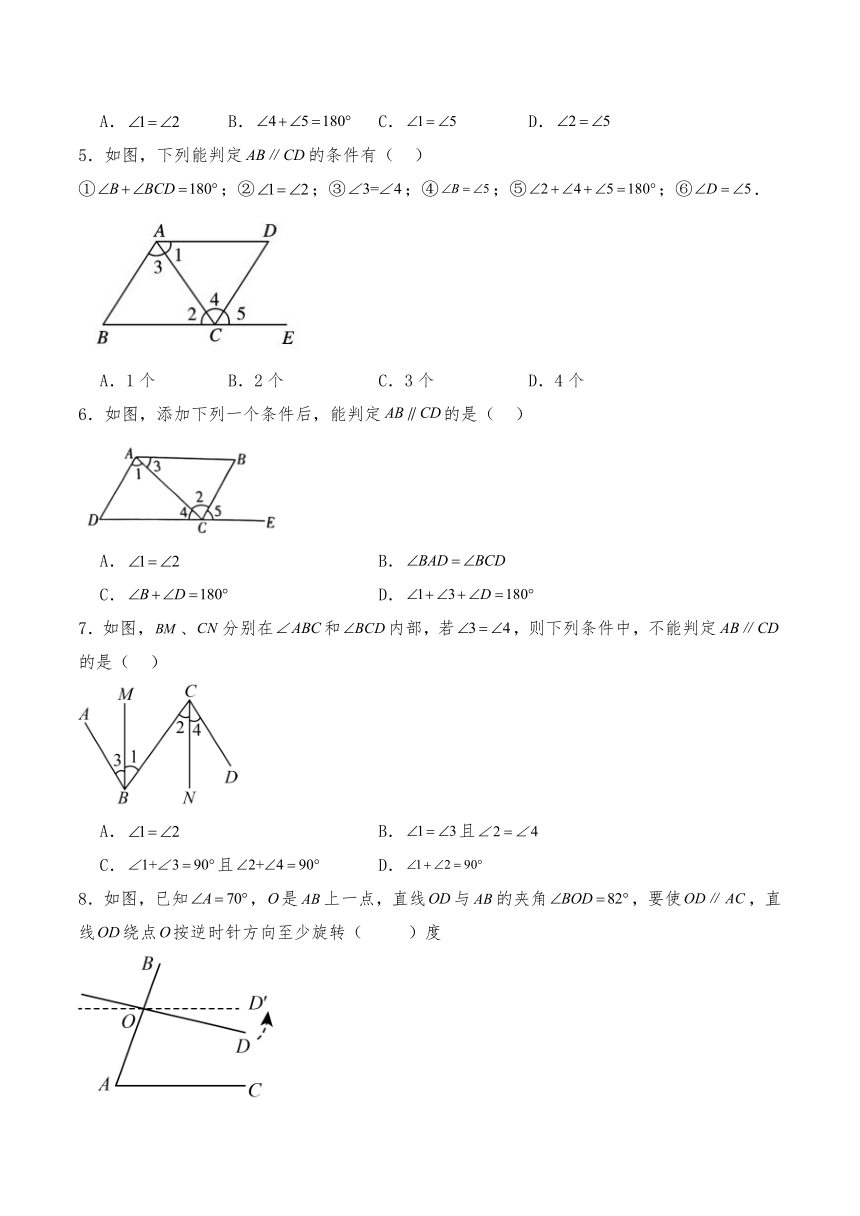
5.如图,下列能判定的条件有( )
①;②;③;④;⑤;⑥.
A.1个 B.2个 C.3个 D.4个
6.如图,添加下列一个条件后,能判定的是( )
A. B.
C. D.
7.如图,、分别在和内部,若,则下列条件中,不能判定的是( )
A. B.且
C.且 D.
8.如图,已知,是上一点,直线与的夹角,要使,直线绕点按逆时针方向至少旋转( )度
A. B. C. D.
9.如图,将一副三角尺如图放置,、交于点,(,)则下列结论不正确的是( )
A. B.
C.若,则 D.若,则
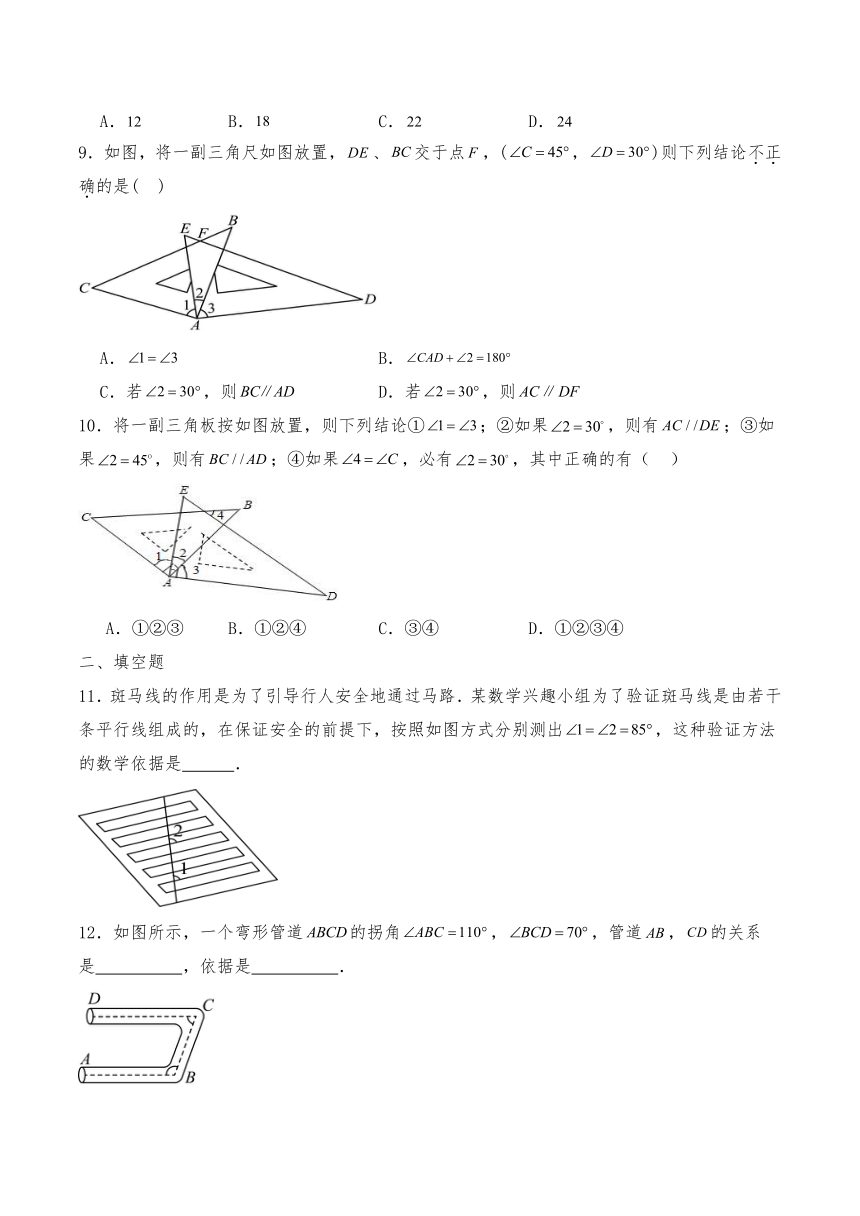
10.将一副三角板按如图放置,则下列结论①;②如果,则有;③如果,则有;④如果,必有,其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
二、填空题
11.斑马线的作用是为了引导行人安全地通过马路.某数学兴趣小组为了验证斑马线是由若干条平行线组成的,在保证安全的前提下,按照如图方式分别测出,这种验证方法的数学依据是 .
12.如图所示,一个弯形管道的拐角,,管道,的关系是 ,依据是 .
13.如图,工人师傅移动角尺在工件上画出直线,其中的道理是 .
14.如图,已知,直线经过点A,请写出一个能判定的条件 .(写出一个即可)
15.如图,下列错误的是 (填序号).
①如果,那么; ②如果,那么;
③如果,那么; ④如果,那么;
⑤如果,那么.
16.一节数学实践课上,老师让同学们用两个大小、形状都相同的三角板画平行线、,并要说出自己做法的依据.小奇、小妙两位同学的做法如图:小奇说:“我做法的依据是:同位角相等,两直线平行.”则小妙做法的依据是 .
17.如图,∠EFB=∠GHD=53°,∠IGA=127°,由这些条件,能找到 对平行线.
三、解答题
18.如图,已知直线被直线所截,平分,平分,,吗?为什么?
因为平分,平分(已知),
所以___________,___________,
所以___________( ),
因为( ),
所以___________,
所以( ).
19.如图所示,直线相交于点O,平分,平分,,垂足为点H,与平行吗?说明理由.
20.如图,的平分线交于E,交于点F,且.
(1)试说明:.
(2)若,求的度数.
21.如图,已知点O在直线AB上,射线OE平分∠AOC,过点O作OD⊥OE,G是射线OB上一点,连接DG,使∠ODG+∠DOG=90°.
(1)求证:∠AOE=∠ODG;
(2)若∠ODG=∠C,试判断CD与OE的位置关系,并说明理由.
22.如图,直线与直线,分别相交于点M,O,,分别平分和,与交于点P,Q,已知.
(1)若,求的度数;
(2)对说明理由.
答案
一、单选题
1.D
【分析】根据平行线的判定与性质、平行公理的推论判断求解即可.
【详解】解:若,则,故A错误,不符合题意;
若,则,故B错误,不符合题意;
若,则,故C错误,不符合题意;
若,则,故D正确,符合题意;
故选:D.
2.C
【分析】利用基本作图方法得出作直线的步骤即可.
【详解】解:②用三角板的斜边靠上直线;
④用直尺紧靠三角板的一条直角边;
①固定直尺,并沿方向移动三角板,使斜边经过点;
③沿三角板斜边画直线;
故选:C.
3.A
【分析】本题主要考查了平行线的判定,根据题意画出对应的示意图,结合平行线的判定条件进行求解即可.
【详解】解:A.如图所示,
由图可知,两次转弯后,行驶方向与原来相同,故A符合题意;
B.如图所示,
由图可知,两次转弯后,行驶方向与原来不相同,故B不符合题意;
C.如图所示,
由图可知,两次转弯后,行驶方向与原来不相同,故C不符合题意;
D.如图所示,
由图可知,两次转弯后,行驶方向与原来不相同,故D不符合题意.
故选A.
4.D
【分析】本题考查的是平行线的判定,由结合内错角相等,两直线平行可得,由结合同旁内角互补,两直线平行可得,由而且两个角不是内错角,不是同位角,不能判定两直线平行,由同理可得,熟记平行线的判定方法是解本题的关键.
【详解】解:∵,
∴,故A不符合题意;
∵,
∴,故B不符合题意;
由,不能判定,故C不符合题意;
∵,
∴,故D符合题意;
故选:D.
5.C
6.D
【分析】本题考查了平行线的判定,熟练掌握判断定理是解题的关键,逐一验证即可.
【详解】A. ,则,不符合题意;
B. ,无法判定,不符合题意;
C. ,无法判定,不符合题意;
D. ,则,符合题意;
故选D.
7.D
【分析】根据“内错角相等,两直线平行”,进行逐一判断即可求解.
【详解】A.因为,,所以,所以,由“内错角相等,两直线平行” ,可得,故此项不符合题意;
B.因为且,,所以,由A可得,故此项不符合题意;
C.因为且,所以,由“内错角相等,两直线平行” ,可得,故此项不符合题意;
D.由无法判断,故此项符合题意;
故选:D.
8.A
【分析】根据,运用两直线平行,同位角相等,求得,即可得到的度数,即旋转角的度数.
【详解】解:∵,
∴,
∴.
故选:A.
9.C
【分析】由余角的性质,得到,由,得到,因为,故和不平行,由,得到.
【详解】解: ++,
,
故A正确;
,
,故B正确;
,
,
,
,
和不平行,
故C错误;
,
,
,
,
,
故D正确.
故选:C.
10.D
【分析】根据∠1+∠2=∠3+∠2即可证得①;根据求出∠1与∠E的度数大小即可判断②;利用∠2求出∠3,与∠B的度数大小即可判断③;利用求出∠1,即可得到∠2的度数,即可判断④.
【详解】∵∠1+∠2=∠3+∠2=90,
∴∠1=∠3,故①正确;
∵,
∴
∠E=60,
∴∠1=∠E,
∴AC∥DE,故②正确;
∵,
∴,
∵,
∴∠3=∠B,
∴,故③正确;
∵,
∴∠CFE=∠C,
∵∠CFE+∠E=∠C+∠1,
∴∠1=∠E=,
∴∠2=90-∠1=,故④正确,
故选:D.
二、填空题
11.同位角相等 ,两直线平行
【分析】由图可得和是一对同位角,根据平行线的判定方法即可求解.
【详解】解:∵,
∴斑马线互相平行. (同位角相等 ,两直线平行)
故答案为:同位角相等 ,两直线平行.
12. 同旁内角互补,两直线平行
【分析】根据题意推出,即可根据同旁内角互补,两直线平行得出结论.
【详解】解:∵,,
∴,
∴(同旁内角互补,两直线平行).
故答案为:,同旁内角互补,两直线平行.
13.同位角相等,两直线平行
【分析】根据平行线的判定定理求解即可.
【详解】解:,
(同位角相等,两直线平行),
故答案为:同位角相等,两直线平行.
14.(答案不唯一)
【分析】由平行线的判定,即可得到答案.
【详解】能判定的条件有,,,.
故答案为:(答案不唯一).
15.③⑤
【分析】①②④可根据同位角相等,两直线平行即可判定;③⑤中两角都不是同位角、内错角或同旁内角,故无法判定平行关系.
【详解】解:①②④都可根据同位角相等,两直线平行证明正确;
因为③⑤中两角都不是同位角、内错角或同旁内角,故无法判定平行关系.
故答案为:③⑤.
16.内错角相等,两直线平行
【分析】本题考查了平行线的判定;根据题意,,得出,即可求解.
【详解】解:∵根据题意,,
∴,依据为:内错角相等,两直线平行
故答案为:内错角相等,两直线平行.
17.2
【分析】根据平行线的判定定理(同位角相等,两直线平行)进行判断即可.
【详解】解:∵∠GHD=53°,
∵∠GHC=127°,
∵∠IGA=127°,
∴∠GHC=∠IGA,∠IGB=53°,
∴AB∥CD,
∵∠EFB=53°,
∴∠IGB=∠EFB,
∴IH∥EF.
故答案为:2.
三、解答题
18.解:因为平分,平分(已知),
所以,,
所以(等量代换),
因为(已知),
所以,
所以(同旁内角互补,两直线平行).
19.解:,理由如下:
∵平分,平分,
∴,,
∵,
∴,即,
∵,
∴.
20.(1)证明:∵平分,
∴,
∵,
∴,
∴(同旁内角互补,两直线平行);
(2)解:∵,,
∴,
∵,
∴,
∴.
21.(1)证明:∵OD⊥OE,
∴∠EOC+∠COD=∠AOE+∠DOG=90°,
∵∠ODG+∠DOG=90°,
∴∠AOE=∠ODG;
(2)解:CDOE.理由如下:
由(1)得∠AOE=∠ODG,
∵射线OE平分∠AOC,
∴∠AOE=∠EOC,
∵∠ODG=∠C,
∴∠EOC=∠C,
∴CDOE.
22.(1)解:∵平分,
∴,
∵,
∴设,则,
∴,
解得:,
∴;
(2)证明:∵,分别平分和,
∴,,
∴,
∵,
∴,
∴.
一、单选题
1.在同一平面内,是直线,下列关于它们位置关系的说法中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.如图,已知直线外一点,过点画直线,使,借助三角板有如下操作:
①固定直尺,并沿方向移动三角板,使斜边经过点;
②用三角板的斜边靠上直线;
③沿三角板斜边画直线;
④用直尺紧靠三角板的一条直角边.
正确的操作顺序是( )
A.①②③④ B.②④③① C.②④①③ D.④③②①
3.一学员练习驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,则这两次拐弯的角度可能是( )
A.第一次向左拐,第二次向右拐
B.第一次向右拐,第二次向左拐
C.第一次向右拐,第二次向右拐
D.第一次向左拐,第二次向左拐
4.如图,在中,点D,E,F分别在边,,上,则下列条件中,能判定的是( )
A. B. C. D.
5.如图,下列能判定的条件有( )
①;②;③;④;⑤;⑥.
A.1个 B.2个 C.3个 D.4个
6.如图,添加下列一个条件后,能判定的是( )
A. B.
C. D.
7.如图,、分别在和内部,若,则下列条件中,不能判定的是( )
A. B.且
C.且 D.
8.如图,已知,是上一点,直线与的夹角,要使,直线绕点按逆时针方向至少旋转( )度
A. B. C. D.
9.如图,将一副三角尺如图放置,、交于点,(,)则下列结论不正确的是( )
A. B.
C.若,则 D.若,则
10.将一副三角板按如图放置,则下列结论①;②如果,则有;③如果,则有;④如果,必有,其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
二、填空题
11.斑马线的作用是为了引导行人安全地通过马路.某数学兴趣小组为了验证斑马线是由若干条平行线组成的,在保证安全的前提下,按照如图方式分别测出,这种验证方法的数学依据是 .
12.如图所示,一个弯形管道的拐角,,管道,的关系是 ,依据是 .
13.如图,工人师傅移动角尺在工件上画出直线,其中的道理是 .
14.如图,已知,直线经过点A,请写出一个能判定的条件 .(写出一个即可)
15.如图,下列错误的是 (填序号).
①如果,那么; ②如果,那么;
③如果,那么; ④如果,那么;
⑤如果,那么.
16.一节数学实践课上,老师让同学们用两个大小、形状都相同的三角板画平行线、,并要说出自己做法的依据.小奇、小妙两位同学的做法如图:小奇说:“我做法的依据是:同位角相等,两直线平行.”则小妙做法的依据是 .
17.如图,∠EFB=∠GHD=53°,∠IGA=127°,由这些条件,能找到 对平行线.
三、解答题
18.如图,已知直线被直线所截,平分,平分,,吗?为什么?
因为平分,平分(已知),
所以___________,___________,
所以___________( ),
因为( ),
所以___________,
所以( ).
19.如图所示,直线相交于点O,平分,平分,,垂足为点H,与平行吗?说明理由.
20.如图,的平分线交于E,交于点F,且.
(1)试说明:.
(2)若,求的度数.
21.如图,已知点O在直线AB上,射线OE平分∠AOC,过点O作OD⊥OE,G是射线OB上一点,连接DG,使∠ODG+∠DOG=90°.
(1)求证:∠AOE=∠ODG;
(2)若∠ODG=∠C,试判断CD与OE的位置关系,并说明理由.
22.如图,直线与直线,分别相交于点M,O,,分别平分和,与交于点P,Q,已知.
(1)若,求的度数;
(2)对说明理由.
答案
一、单选题
1.D
【分析】根据平行线的判定与性质、平行公理的推论判断求解即可.
【详解】解:若,则,故A错误,不符合题意;
若,则,故B错误,不符合题意;
若,则,故C错误,不符合题意;
若,则,故D正确,符合题意;
故选:D.
2.C
【分析】利用基本作图方法得出作直线的步骤即可.
【详解】解:②用三角板的斜边靠上直线;
④用直尺紧靠三角板的一条直角边;
①固定直尺,并沿方向移动三角板,使斜边经过点;
③沿三角板斜边画直线;
故选:C.
3.A
【分析】本题主要考查了平行线的判定,根据题意画出对应的示意图,结合平行线的判定条件进行求解即可.
【详解】解:A.如图所示,
由图可知,两次转弯后,行驶方向与原来相同,故A符合题意;
B.如图所示,
由图可知,两次转弯后,行驶方向与原来不相同,故B不符合题意;
C.如图所示,
由图可知,两次转弯后,行驶方向与原来不相同,故C不符合题意;
D.如图所示,
由图可知,两次转弯后,行驶方向与原来不相同,故D不符合题意.
故选A.
4.D
【分析】本题考查的是平行线的判定,由结合内错角相等,两直线平行可得,由结合同旁内角互补,两直线平行可得,由而且两个角不是内错角,不是同位角,不能判定两直线平行,由同理可得,熟记平行线的判定方法是解本题的关键.
【详解】解:∵,
∴,故A不符合题意;
∵,
∴,故B不符合题意;
由,不能判定,故C不符合题意;
∵,
∴,故D符合题意;
故选:D.
5.C
6.D
【分析】本题考查了平行线的判定,熟练掌握判断定理是解题的关键,逐一验证即可.
【详解】A. ,则,不符合题意;
B. ,无法判定,不符合题意;
C. ,无法判定,不符合题意;
D. ,则,符合题意;
故选D.
7.D
【分析】根据“内错角相等,两直线平行”,进行逐一判断即可求解.
【详解】A.因为,,所以,所以,由“内错角相等,两直线平行” ,可得,故此项不符合题意;
B.因为且,,所以,由A可得,故此项不符合题意;
C.因为且,所以,由“内错角相等,两直线平行” ,可得,故此项不符合题意;
D.由无法判断,故此项符合题意;
故选:D.
8.A
【分析】根据,运用两直线平行,同位角相等,求得,即可得到的度数,即旋转角的度数.
【详解】解:∵,
∴,
∴.
故选:A.
9.C
【分析】由余角的性质,得到,由,得到,因为,故和不平行,由,得到.
【详解】解: ++,
,
故A正确;
,
,故B正确;
,
,
,
,
和不平行,
故C错误;
,
,
,
,
,
故D正确.
故选:C.
10.D
【分析】根据∠1+∠2=∠3+∠2即可证得①;根据求出∠1与∠E的度数大小即可判断②;利用∠2求出∠3,与∠B的度数大小即可判断③;利用求出∠1,即可得到∠2的度数,即可判断④.
【详解】∵∠1+∠2=∠3+∠2=90,
∴∠1=∠3,故①正确;
∵,
∴
∠E=60,
∴∠1=∠E,
∴AC∥DE,故②正确;
∵,
∴,
∵,
∴∠3=∠B,
∴,故③正确;
∵,
∴∠CFE=∠C,
∵∠CFE+∠E=∠C+∠1,
∴∠1=∠E=,
∴∠2=90-∠1=,故④正确,
故选:D.
二、填空题
11.同位角相等 ,两直线平行
【分析】由图可得和是一对同位角,根据平行线的判定方法即可求解.
【详解】解:∵,
∴斑马线互相平行. (同位角相等 ,两直线平行)
故答案为:同位角相等 ,两直线平行.
12. 同旁内角互补,两直线平行
【分析】根据题意推出,即可根据同旁内角互补,两直线平行得出结论.
【详解】解:∵,,
∴,
∴(同旁内角互补,两直线平行).
故答案为:,同旁内角互补,两直线平行.
13.同位角相等,两直线平行
【分析】根据平行线的判定定理求解即可.
【详解】解:,
(同位角相等,两直线平行),
故答案为:同位角相等,两直线平行.
14.(答案不唯一)
【分析】由平行线的判定,即可得到答案.
【详解】能判定的条件有,,,.
故答案为:(答案不唯一).
15.③⑤
【分析】①②④可根据同位角相等,两直线平行即可判定;③⑤中两角都不是同位角、内错角或同旁内角,故无法判定平行关系.
【详解】解:①②④都可根据同位角相等,两直线平行证明正确;
因为③⑤中两角都不是同位角、内错角或同旁内角,故无法判定平行关系.
故答案为:③⑤.
16.内错角相等,两直线平行
【分析】本题考查了平行线的判定;根据题意,,得出,即可求解.
【详解】解:∵根据题意,,
∴,依据为:内错角相等,两直线平行
故答案为:内错角相等,两直线平行.
17.2
【分析】根据平行线的判定定理(同位角相等,两直线平行)进行判断即可.
【详解】解:∵∠GHD=53°,
∵∠GHC=127°,
∵∠IGA=127°,
∴∠GHC=∠IGA,∠IGB=53°,
∴AB∥CD,
∵∠EFB=53°,
∴∠IGB=∠EFB,
∴IH∥EF.
故答案为:2.
三、解答题
18.解:因为平分,平分(已知),
所以,,
所以(等量代换),
因为(已知),
所以,
所以(同旁内角互补,两直线平行).
19.解:,理由如下:
∵平分,平分,
∴,,
∵,
∴,即,
∵,
∴.
20.(1)证明:∵平分,
∴,
∵,
∴,
∴(同旁内角互补,两直线平行);
(2)解:∵,,
∴,
∵,
∴,
∴.
21.(1)证明:∵OD⊥OE,
∴∠EOC+∠COD=∠AOE+∠DOG=90°,
∵∠ODG+∠DOG=90°,
∴∠AOE=∠ODG;
(2)解:CDOE.理由如下:
由(1)得∠AOE=∠ODG,
∵射线OE平分∠AOC,
∴∠AOE=∠EOC,
∵∠ODG=∠C,
∴∠EOC=∠C,
∴CDOE.
22.(1)解:∵平分,
∴,
∵,
∴设,则,
∴,
解得:,
∴;
(2)证明:∵,分别平分和,
∴,,
∴,
∵,
∴,
∴.
同课章节目录
