人教版数学七年级下册第八章实数单元检测卷(含解析)
文档属性
| 名称 | 人教版数学七年级下册第八章实数单元检测卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 608.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-05 21:55:49 | ||
图片预览




文档简介
第八章 实 数(单元检测卷)
一、选择题(每题3分,共24分)
1.4的算术平方根是 ( )
A. B.2 C. D.
2.将边长分别为 和 的长方形如图剪开,拼成一个与长方形面积相等的正方形,则该正方形的边长是 ( )
A. B. C. D.
3.估计的值在 ( )
A.3和4之间 B.4和5之间 C.5和6之间 D.6和7之间
4.已知一个正方体的体积扩大为原来的n倍,它的棱长变为原来的 ( )
A.倍 B.倍 C.3n倍 D.n3倍
5.在实数:3.14159,,1.010010001,,π,中,是无理数的共 ( )
A.1个 B.2个 C.3个 D.4个
6.下列说法正确的是 ( )
A.的立方根是8
B.是负数所以没有立方根
C.不是正数就是负数
D.0.09的算术平方根是0.3
7.若,且,则的值为 ( )
A.或 B.或10 C.4或10 D.4或
8.如图是用4个相同的长方形与1个正方形镶嵌而成的正方形图案.已知该图案的总面积为m,小正方形的面积为n.若用x、y表示长方形的两边长(),请观察图案,指出下列关系式:①、②、③、④若,则.这四个结论中正确的有( )个
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
9.的立方根是______.
10.若,则的立方根为__________.
11.比较大小:3______.
12.点A,B在数轴上,以AB为边作正方形,该正方形的面积是7.若点A对应的数是-2,则点B对应的数是__________.
13.若,则_____.
14.若是16的一个平方根,则x的值为 _____ .
15.已知的整数部分是的小数部分是,则_____.
16.已知表示数的点在数轴上的位置如图所示,则=________.
三、解答题(每题8分,共72分)
17.计算:
(1); (2).
18.已知的平方根是,的立方根是2,求的平方根.
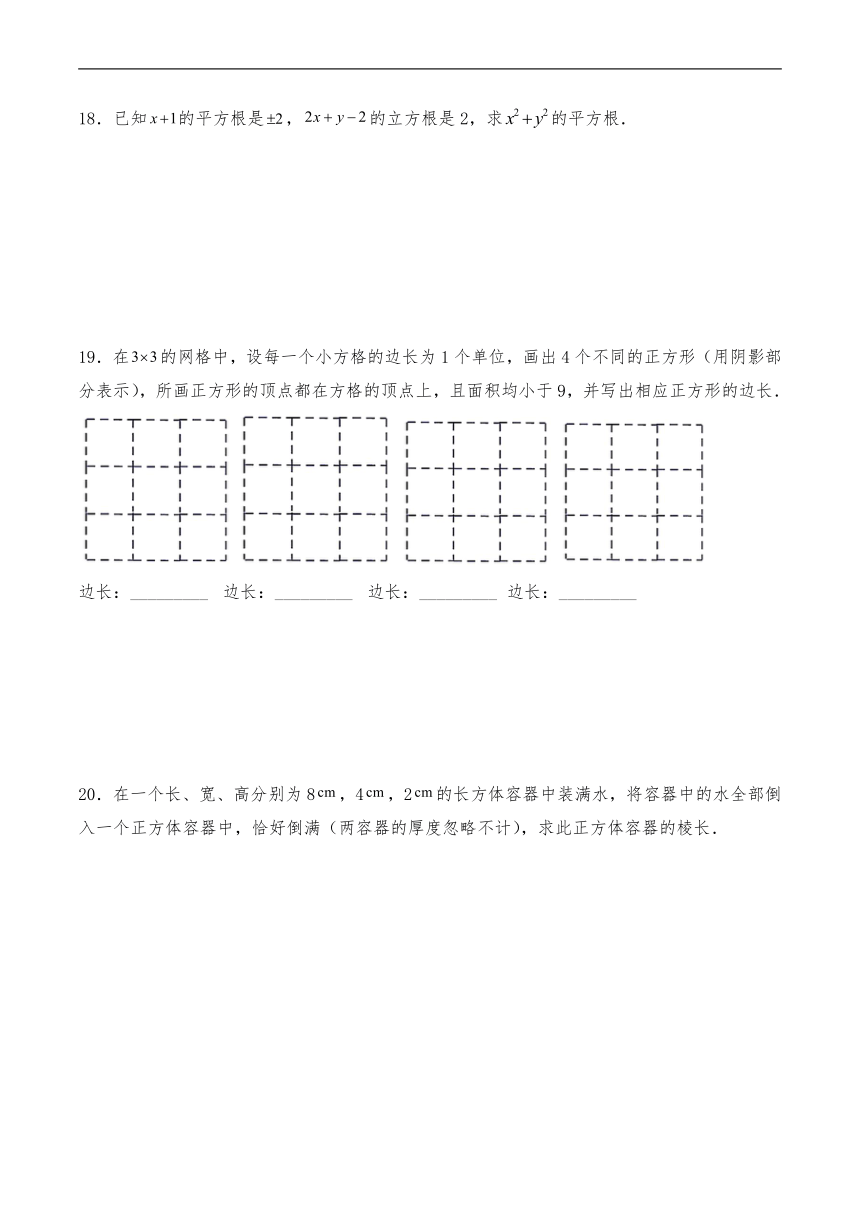
19.在的网格中,设每一个小方格的边长为1个单位,画出4个不同的正方形(用阴影部分表示),所画正方形的顶点都在方格的顶点上,且面积均小于9,并写出相应正方形的边长.
边长:_________ 边长:_________ 边长:_________ 边长:_________
20.在一个长、宽、高分别为8,4,2的长方体容器中装满水,将容器中的水全部倒入一个正方体容器中,恰好倒满(两容器的厚度忽略不计),求此正方体容器的棱长.
21.已知正数a的两个平方根分别是和,与互为相反数,求的值.
22.我们知道,平方数的开平方运算可以直接求得,如等,有些数则不能直接求得,如,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得,请你观察下表:
a … 0.04 4 400 40000 …
… x 2 y z …
(1)表格中的三个值分别为:x= ;y= ;z= ;
(2)用公式表示这一规律:当a=4×100n(n为整数)时,= ;
(3)利用这一规律,解决下面的问题:
已知,则①≈ ;②≈ .
23.化简求值:
(1)已知a是的整数部分,,求的平方根.
(2)已知:实数a,b在数轴上的位置如图所示,化简:.
24.如图,已知A、B两点在数轴上对应的数分别为和1.
(1)点A到点B的距离为______.
(2)数轴上存在一点M,使M到A的距离是M到B距离的2倍,求点M所表示的数.
(3)在点B右侧的数轴上取点D,使D到B的距离是个单位长度,如果点D所表示的数的整数部分为a,小数部分为b,求的绝对值.
25.定义:若,则称与是关于的关联数.例如:若,则称与是关于2的关联数.
(1)若49与是关于2的关联数,则________;
(2)若与是关于2的关联数,求的平方根;
(3)若与是关于的关联数,,的值与无关,求的值.
答案
一、选择题
1.
【分析】根据算术平方根的性质,即可求解.
【解析】解∶ 4的算术平方根是2.
故选:B
2.
【分析】因为正方形的面积与长方形的面积相等,可知正方形的边长.
【解析】解:∵长方形的长为,宽为
∴长方形的面积:
设正方形的边长为,则可得:
∴
∵是正方形的边长,即
∴
故选:
3.
【分析】利用进行判断即可.
【解析】解:∵,
∴,
故选:C.
4.
【分析】设正方体的原体积为1,则此时原棱长为1,再由扩大后的体积求出扩大后的棱长,然后比较即可.
【解析】设正方体的原体积为1,
根据正方体体积公式可知此时原棱长为1,
体积扩大为原来的n倍后,体积为n,
此时棱长为,
棱长变为原来的,
故选A.
5.
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【解析】解:,
∴无理数有,π,共2个.
故选:B.
6.
【分析】先明确立方根和算术平方根的概念,再进行判断.
【解析】A.,它的立方根为2,A选项错误,所以A选项不符合题意;
B.是负数,负数也有立方根,B选项错误,所以B选项不符合题意;
C.可能是正数、负数、0,C选项错误,所以C选项不符合题意;
D.0.09的算术平方根是0.3,D选项正确,所以D选项符合题意.
故选:D.
7.
【分析】由平方根和绝对值的定义可求出x和y的值,再根据,舍去不合题意的x和y的值,最后代入中求值即可.
【解析】∵,
∴.
∵,
∴.
∴当时,;
当时,.
综上可知的值为或.
故选A.
8.
【分析】根据该图案的总面积、正方形的面积公式即可判断①;根据小正方形的面积、正方形的面积公式可得,从而可得,再结合①即可判断②;根据四个长方形的面积等于两个正方形的面积之差即可判断③;先将用含的式子表示出来,由此即可判断④.
【解析】解:该图案是正方形,且该图案的总面积为,边长为,
,结论①正确;
小正方形的面积为,边长为,
,
由得:,
则,即,结论②正确;
四个长方形的面积等于两个正方形的面积之差,
,即,结论③正确;
由结论②可知,,
代入得:,
若,则,即,
,结论④错误;
综上,这四个结论中正确的有3个,
故选:C.
二、填空题
9.
【分析】先求出,再根据立方根的性质,即可求解.
【解析】解:,的立方根为,
故答案为:
10.
【分析】根据二次根式,绝对值的非负性即可求解.
【解析】解:∵,,
∴,,
∴,,
∴,
∴,
故答案为:.
11.
【分析】根据实数的大小比较法则,即可求解.
【解析】解:∵,
∴.
故答案为:
12.
【分析】先求出AB的长,再设B点表示的数为,根据数轴上两点间的距离公式求出的值即可.
【解析】∵正方形的面积是7,
∴,
设B点表示的数为,
∵点A对应的数是,
∴,
解得,
故答案为:.
13.
【分析】根据平方根和立方根的定义即可求出a,b的值,进一步计算即可.
【解析】解:因为,
所以,,
所以或.
故答案为:或5.
14.
【分析】根据平方根的定义,可得,进而即可求解.
【解析】解:∵是16的一个平方根,
∴,
∴x的值为3或.
15.
【分析】估计和的范围即可确定,的值,进而求得的值.
【解析】解:∵,
∴的整数部分是,,
∵的整数部分是的小数部分是,
∴,,
∴,
故答案为:
16.
【分析】先判断出的正负性,再去绝对值即可得出答案.
【解析】解:∵,
∴,
由数轴可知:,
∴,
∴,
故答案为:.
三、解答题
17.(1)解:
(2)解:
18.解∶∵的平方根是,
∴,
∴,
又∵的立方根是2,
∴
∴.
∴.
∴的平方根为.
19.解:如图,
∵正方形的面积为,此时边长为:,
∵正方形的面积为:,所以此时边长为,
此时正方形的边长为2,
此时正方形的边长为1.
20.解:由于装满水的长方体容器中的水,全部倒入正方体容器中,恰好倒满,
所以它们的体积相等,
而长方体容器的体积,
所以正方体容器的体积为64,
所以此正方体容器的棱长为.
21.解:∵正数a的两个平方根分别是和,
∴,解得:.
∴,
∴,
∵,与互为相反数,
∴,解得:.
当时,.
22.(1)解:根据算术平方根定义可得:.
故答案为.
(2)解:当(n为整数)时,.
故答案为.
(3)解:若,则①;②.
故答案为:.
23.(1)∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴的平方根是;
(2)由数轴可得:,
则,
则
.
24.(1)点A到点B的距离为:,
故答案为4;
(2)设点M表示的数为x,
则点M到点A的距离为,点M到点B距离为,
∵M到A的距离是M到B距离的2倍,
∴,
则或,
解得:或,
综上所述:点M所表示的数为5或;
(3)根据题意可得:点D所表示的数为,
∵,
∴,
∴,
∵点D所表示的数的整数部分为a,小数部分为b,
∴,
∴,
∵
∴,
∴,
综上所述:的绝对值为.
25.(1)解:由题意可得:
解得,
故答案为:;
(2)由题意可得:
解得:,
的平方根为
(3)由题意可得:,
则,
∵的值与无关
∴,解得
则
一、选择题(每题3分,共24分)
1.4的算术平方根是 ( )
A. B.2 C. D.
2.将边长分别为 和 的长方形如图剪开,拼成一个与长方形面积相等的正方形,则该正方形的边长是 ( )
A. B. C. D.
3.估计的值在 ( )
A.3和4之间 B.4和5之间 C.5和6之间 D.6和7之间
4.已知一个正方体的体积扩大为原来的n倍,它的棱长变为原来的 ( )
A.倍 B.倍 C.3n倍 D.n3倍
5.在实数:3.14159,,1.010010001,,π,中,是无理数的共 ( )
A.1个 B.2个 C.3个 D.4个
6.下列说法正确的是 ( )
A.的立方根是8
B.是负数所以没有立方根
C.不是正数就是负数
D.0.09的算术平方根是0.3
7.若,且,则的值为 ( )
A.或 B.或10 C.4或10 D.4或
8.如图是用4个相同的长方形与1个正方形镶嵌而成的正方形图案.已知该图案的总面积为m,小正方形的面积为n.若用x、y表示长方形的两边长(),请观察图案,指出下列关系式:①、②、③、④若,则.这四个结论中正确的有( )个
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
9.的立方根是______.
10.若,则的立方根为__________.
11.比较大小:3______.
12.点A,B在数轴上,以AB为边作正方形,该正方形的面积是7.若点A对应的数是-2,则点B对应的数是__________.
13.若,则_____.
14.若是16的一个平方根,则x的值为 _____ .
15.已知的整数部分是的小数部分是,则_____.
16.已知表示数的点在数轴上的位置如图所示,则=________.
三、解答题(每题8分,共72分)
17.计算:
(1); (2).
18.已知的平方根是,的立方根是2,求的平方根.
19.在的网格中,设每一个小方格的边长为1个单位,画出4个不同的正方形(用阴影部分表示),所画正方形的顶点都在方格的顶点上,且面积均小于9,并写出相应正方形的边长.
边长:_________ 边长:_________ 边长:_________ 边长:_________
20.在一个长、宽、高分别为8,4,2的长方体容器中装满水,将容器中的水全部倒入一个正方体容器中,恰好倒满(两容器的厚度忽略不计),求此正方体容器的棱长.
21.已知正数a的两个平方根分别是和,与互为相反数,求的值.
22.我们知道,平方数的开平方运算可以直接求得,如等,有些数则不能直接求得,如,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得,请你观察下表:
a … 0.04 4 400 40000 …
… x 2 y z …
(1)表格中的三个值分别为:x= ;y= ;z= ;
(2)用公式表示这一规律:当a=4×100n(n为整数)时,= ;
(3)利用这一规律,解决下面的问题:
已知,则①≈ ;②≈ .
23.化简求值:
(1)已知a是的整数部分,,求的平方根.
(2)已知:实数a,b在数轴上的位置如图所示,化简:.
24.如图,已知A、B两点在数轴上对应的数分别为和1.
(1)点A到点B的距离为______.
(2)数轴上存在一点M,使M到A的距离是M到B距离的2倍,求点M所表示的数.
(3)在点B右侧的数轴上取点D,使D到B的距离是个单位长度,如果点D所表示的数的整数部分为a,小数部分为b,求的绝对值.
25.定义:若,则称与是关于的关联数.例如:若,则称与是关于2的关联数.
(1)若49与是关于2的关联数,则________;
(2)若与是关于2的关联数,求的平方根;
(3)若与是关于的关联数,,的值与无关,求的值.
答案
一、选择题
1.
【分析】根据算术平方根的性质,即可求解.
【解析】解∶ 4的算术平方根是2.
故选:B
2.
【分析】因为正方形的面积与长方形的面积相等,可知正方形的边长.
【解析】解:∵长方形的长为,宽为
∴长方形的面积:
设正方形的边长为,则可得:
∴
∵是正方形的边长,即
∴
故选:
3.
【分析】利用进行判断即可.
【解析】解:∵,
∴,
故选:C.
4.
【分析】设正方体的原体积为1,则此时原棱长为1,再由扩大后的体积求出扩大后的棱长,然后比较即可.
【解析】设正方体的原体积为1,
根据正方体体积公式可知此时原棱长为1,
体积扩大为原来的n倍后,体积为n,
此时棱长为,
棱长变为原来的,
故选A.
5.
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【解析】解:,
∴无理数有,π,共2个.
故选:B.
6.
【分析】先明确立方根和算术平方根的概念,再进行判断.
【解析】A.,它的立方根为2,A选项错误,所以A选项不符合题意;
B.是负数,负数也有立方根,B选项错误,所以B选项不符合题意;
C.可能是正数、负数、0,C选项错误,所以C选项不符合题意;
D.0.09的算术平方根是0.3,D选项正确,所以D选项符合题意.
故选:D.
7.
【分析】由平方根和绝对值的定义可求出x和y的值,再根据,舍去不合题意的x和y的值,最后代入中求值即可.
【解析】∵,
∴.
∵,
∴.
∴当时,;
当时,.
综上可知的值为或.
故选A.
8.
【分析】根据该图案的总面积、正方形的面积公式即可判断①;根据小正方形的面积、正方形的面积公式可得,从而可得,再结合①即可判断②;根据四个长方形的面积等于两个正方形的面积之差即可判断③;先将用含的式子表示出来,由此即可判断④.
【解析】解:该图案是正方形,且该图案的总面积为,边长为,
,结论①正确;
小正方形的面积为,边长为,
,
由得:,
则,即,结论②正确;
四个长方形的面积等于两个正方形的面积之差,
,即,结论③正确;
由结论②可知,,
代入得:,
若,则,即,
,结论④错误;
综上,这四个结论中正确的有3个,
故选:C.
二、填空题
9.
【分析】先求出,再根据立方根的性质,即可求解.
【解析】解:,的立方根为,
故答案为:
10.
【分析】根据二次根式,绝对值的非负性即可求解.
【解析】解:∵,,
∴,,
∴,,
∴,
∴,
故答案为:.
11.
【分析】根据实数的大小比较法则,即可求解.
【解析】解:∵,
∴.
故答案为:
12.
【分析】先求出AB的长,再设B点表示的数为,根据数轴上两点间的距离公式求出的值即可.
【解析】∵正方形的面积是7,
∴,
设B点表示的数为,
∵点A对应的数是,
∴,
解得,
故答案为:.
13.
【分析】根据平方根和立方根的定义即可求出a,b的值,进一步计算即可.
【解析】解:因为,
所以,,
所以或.
故答案为:或5.
14.
【分析】根据平方根的定义,可得,进而即可求解.
【解析】解:∵是16的一个平方根,
∴,
∴x的值为3或.
15.
【分析】估计和的范围即可确定,的值,进而求得的值.
【解析】解:∵,
∴的整数部分是,,
∵的整数部分是的小数部分是,
∴,,
∴,
故答案为:
16.
【分析】先判断出的正负性,再去绝对值即可得出答案.
【解析】解:∵,
∴,
由数轴可知:,
∴,
∴,
故答案为:.
三、解答题
17.(1)解:
(2)解:
18.解∶∵的平方根是,
∴,
∴,
又∵的立方根是2,
∴
∴.
∴.
∴的平方根为.
19.解:如图,
∵正方形的面积为,此时边长为:,
∵正方形的面积为:,所以此时边长为,
此时正方形的边长为2,
此时正方形的边长为1.
20.解:由于装满水的长方体容器中的水,全部倒入正方体容器中,恰好倒满,
所以它们的体积相等,
而长方体容器的体积,
所以正方体容器的体积为64,
所以此正方体容器的棱长为.
21.解:∵正数a的两个平方根分别是和,
∴,解得:.
∴,
∴,
∵,与互为相反数,
∴,解得:.
当时,.
22.(1)解:根据算术平方根定义可得:.
故答案为.
(2)解:当(n为整数)时,.
故答案为.
(3)解:若,则①;②.
故答案为:.
23.(1)∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴的平方根是;
(2)由数轴可得:,
则,
则
.
24.(1)点A到点B的距离为:,
故答案为4;
(2)设点M表示的数为x,
则点M到点A的距离为,点M到点B距离为,
∵M到A的距离是M到B距离的2倍,
∴,
则或,
解得:或,
综上所述:点M所表示的数为5或;
(3)根据题意可得:点D所表示的数为,
∵,
∴,
∴,
∵点D所表示的数的整数部分为a,小数部分为b,
∴,
∴,
∵
∴,
∴,
综上所述:的绝对值为.
25.(1)解:由题意可得:
解得,
故答案为:;
(2)由题意可得:
解得:,
的平方根为
(3)由题意可得:,
则,
∵的值与无关
∴,解得
则
同课章节目录
