人教版八年级数学下册期中模拟试卷(含解析)
文档属性
| 名称 | 人教版八年级数学下册期中模拟试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-06 14:04:24 | ||
图片预览


文档简介
期中模拟试卷
测试范围:二次根式、勾股定理、平行四边形
一、选择题。(共10小题,每小题3分,共30分)
1.使有意义的的取值范围是
A. B. C.x≤2024 D.x≥2024
2.平行四边形的周长为,其中一边长为,则它的邻边长为
A.2 B. C. D.
3.下列二次根式中,不是最简二次根式的是
A. B. C. D.
4.在中,,则
A. B. C. D.
5.下列命题的逆命题是真命题的个数有
①如果两个实数相等,那么它们的绝对值相等;
②全等三角形的对应角相等;
③如果两个角是直角,那么它们相等;
④平行四边形的对角线互相平分;
⑤对顶角相等.
A.0个 B.1个 C.2个 D.3个
6.在中,若,,,则下列条件不能判定是直角三角形的是
A. B.
C.,, D.,
7.下列计算正确的是
A. B. C. D.
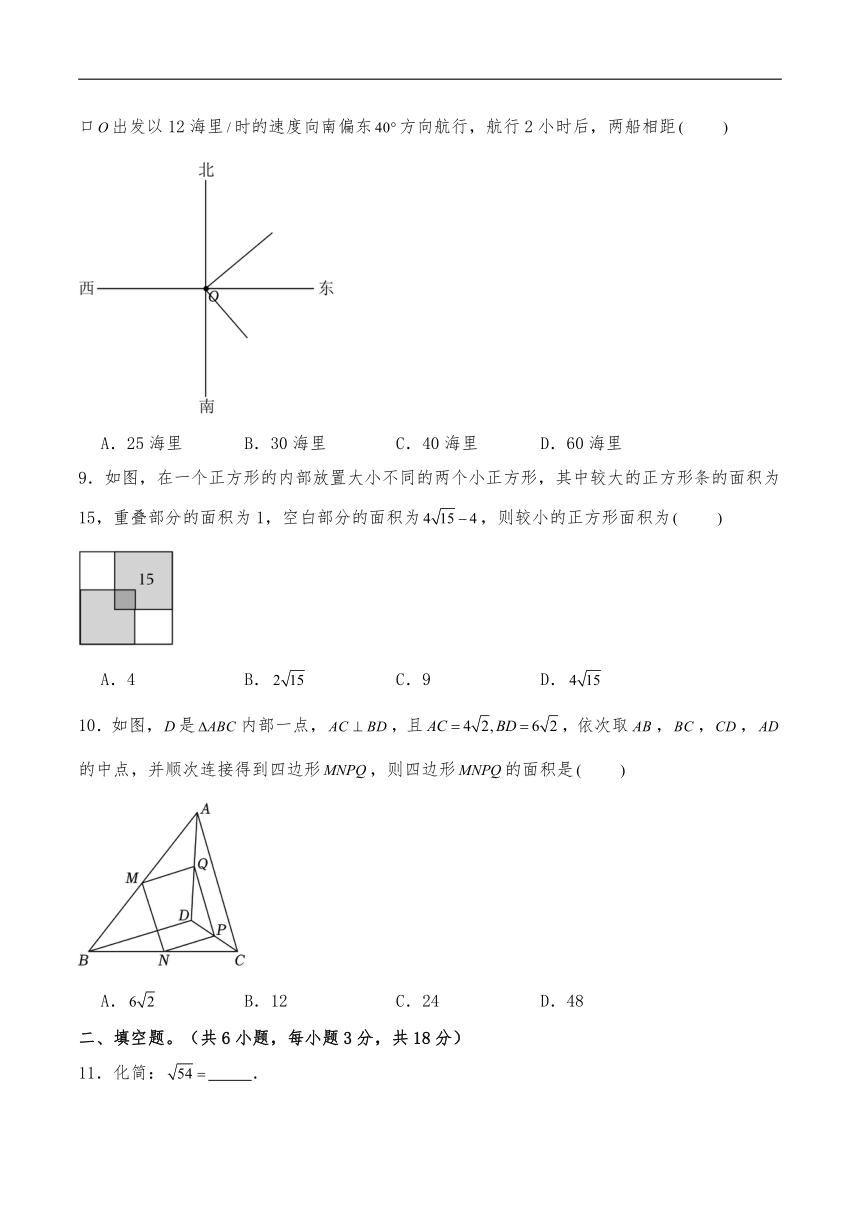
8.如图,一轮船从港口出发以16海里时的速度向北偏东方向航行,另一轮船同时从港口出发以12海里时的速度向南偏东方向航行,航行2小时后,两船相距
A.25海里 B.30海里 C.40海里 D.60海里
9.如图,在一个正方形的内部放置大小不同的两个小正方形,其中较大的正方形条的面积为15,重叠部分的面积为1,空白部分的面积为,则较小的正方形面积为
A.4 B. C.9 D.
10.如图,是内部一点,,且,依次取,,,的中点,并顺次连接得到四边形,则四边形的面积是
A. B.12 C.24 D.48
二、填空题。(共6小题,每小题3分,共18分)
11.化简: .
12.已知是整数,则正整数的最小值为 .
13.直角三角形有两边长分别为3,4,则该直角三角形第三边为 .
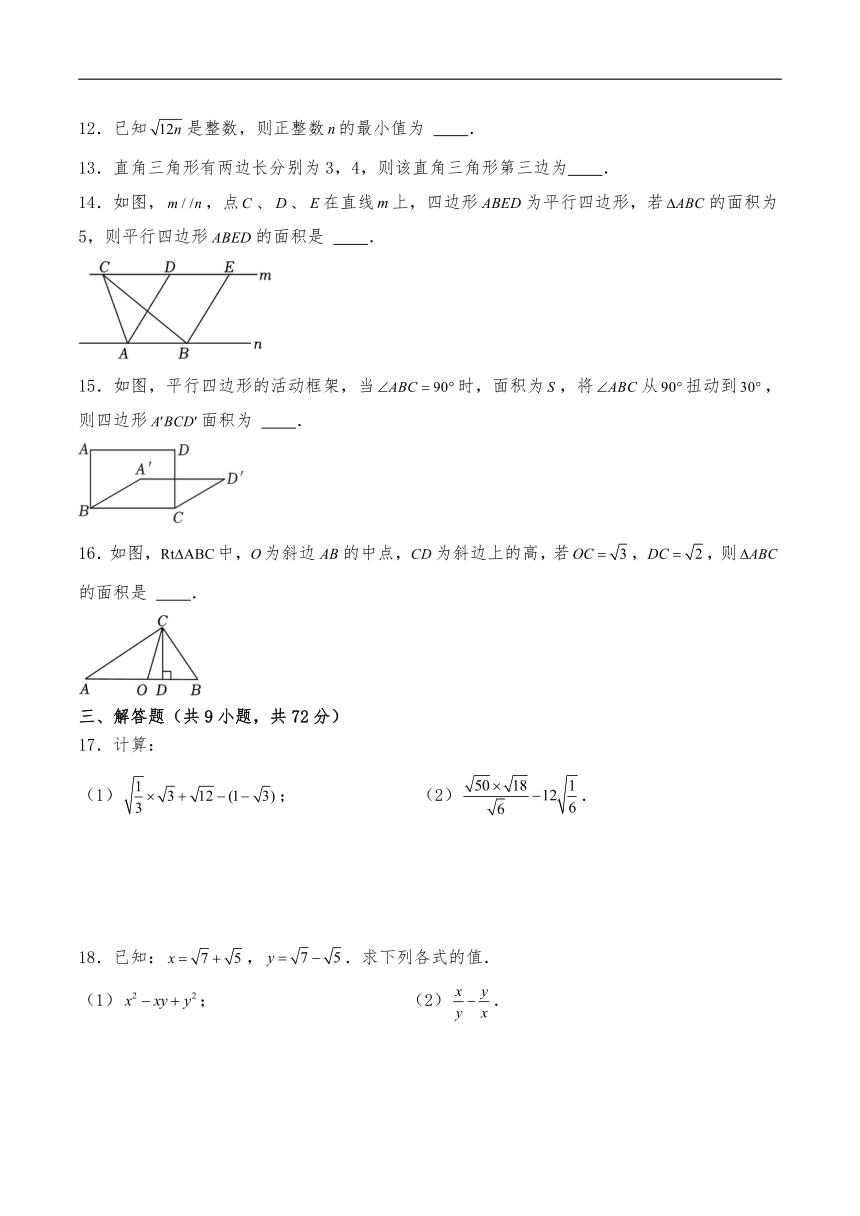
14.如图,,点、、在直线上,四边形为平行四边形,若的面积为5,则平行四边形的面积是 .
15.如图,平行四边形的活动框架,当时,面积为,将从扭动到,则四边形面积为 .
16.如图,中,为斜边的中点,为斜边上的高,若,,则的面积是 .
三、解答题(共9小题,共72分)
17.计算:
(1); (2).
18.已知:,.求下列各式的值.
(1); (2).
19.如图,矩形的对角线,交于点,延长到点,使,延长到点,使,连接,,.
(1)求证:四边形是菱形;
(2)若,,求菱形的面积.
20.如图,平行四边形的对角线与相交于点,点为的中点,过点作交的延长线于点,连接.求证:四边形是平行四边形.
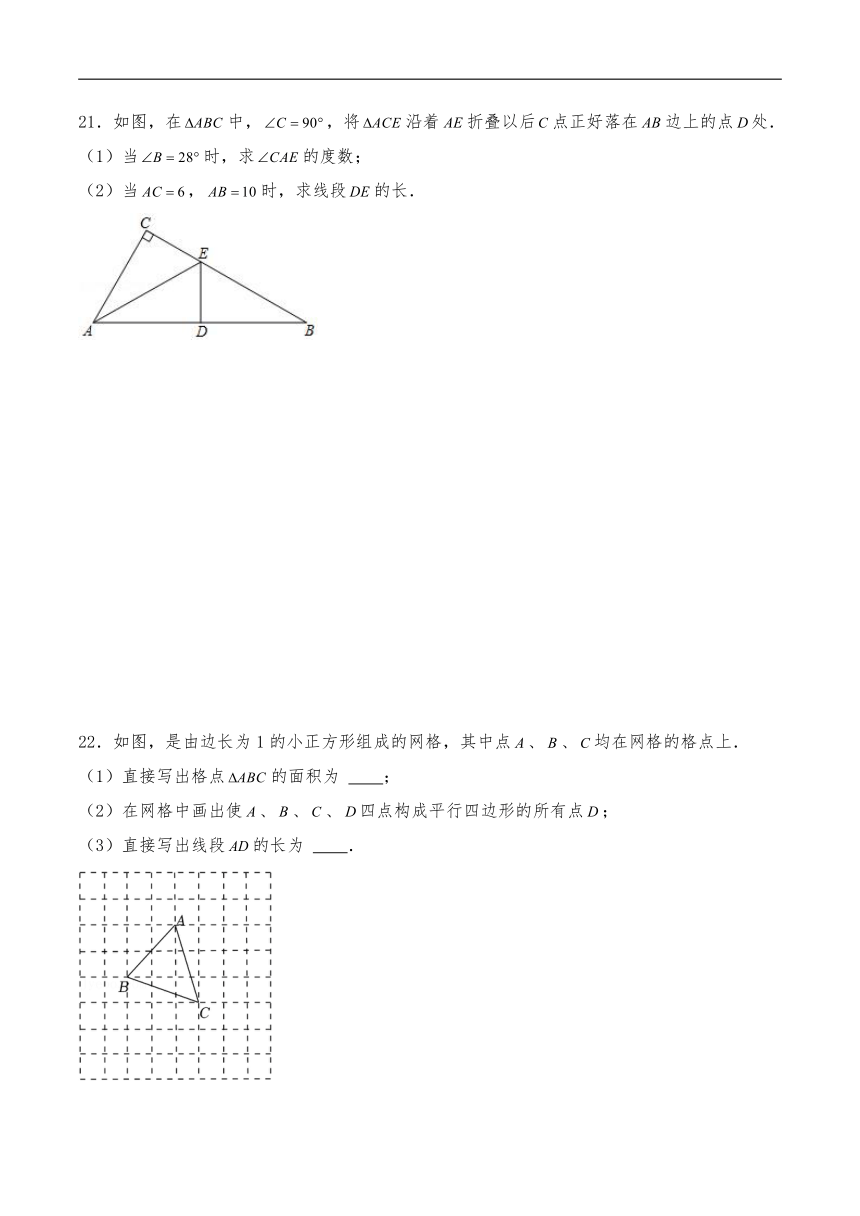
21.如图,在中,,将沿着折叠以后点正好落在边上的点处.
(1)当时,求的度数;
(2)当,时,求线段的长.
22.如图,是由边长为1的小正方形组成的网格,其中点、、均在网格的格点上.
(1)直接写出格点的面积为 ;
(2)在网格中画出使、、、四点构成平行四边形的所有点;
(3)直接写出线段的长为 .
23.已知正方形的边长为4..
(1)如图1,点在直线上运动,连接,将线段绕点按顺时针旋转得到,连接.
①若点与重合,则 .
②若,求的长.
(2)如图2,点在边上不与,重合)运动,且,连接、.将线段绕点逆时针旋转得到,将线段绕点顺时针旋转得到,设,,求关于的函数表达式.
24.(1)已知,,求的值;
(2)若,求的值.
25.如图,在中,,以为边在外作菱形,对角线交于点,连接,.
(1)如图(1),若,,,请直接写出的长;
(2)如图(2),若,求证;
(3)如图(3),若,请直接写出的值.
答案
一、选择题。
1.
【分析】根据二次根式被开方数不小于零条件进行解题即可.
【解答】解:由题可知,
X-2024≥0,
解得x≥2024.
故选:.
2.
【分析】根据平行四边形对边相等即可解决问题.
【解答】解:因为平行四边形的周长为,其中一边长为,
则它的邻边长为.
故选.
3.
【分析】根据最简二次根式的概念判断即可.
【解答】解:、是最简二次根式,不符合题意;
、是最简二次根式,不符合题意;
、,不是最简二次根式,符合题意;
、是最简二次根式,不符合题意;
故选:.
4.
【分析】根据平行四边形的邻角互补即可得出的度数.
【解答】解:根据平行四边形的性质可得:.
故选:.
5.
【分析】分别写出各个命题的逆命题,根据绝对值的性质、全等三角形的判定、平行四边形的判定、对顶角的概念判断即可.
【解答】解:①如果两个实数相等,那么它们的绝对值相等的逆命题是如果两个实数们的绝对值相等,那么这两个实数相等,是假命题;
②全等三角形的对应角相等的逆命题是对应角相等的三角形全等,是假命题;
③如果两个角是直角,那么它们相等的逆命题是如果两个角相等,那么这两个角是直角,是假命题;
④平行四边形的对角线互相平分的逆命题是对角线互相平分的四边形是平行四边形,是真命题;
⑤对顶角相等的逆命题是相等的角是对顶角,是假命题;
故选:.
6.
【分析】根据勾股定理的逆定理,三角形内角和定理进行计算,逐一判断即可解答.
【解答】解:、,
,
是直角三角形,
故不符合题意;
、,
,
,
,
,
是直角三角形,
故不符合题意;
、,,
,
不是直角三角形,
故符合题意;
、,,
,
是直角三角形,
故不符合题意;
故选:.
7.
【分析】根据二次根式的混合运算法则即可得出答案.
【解答】解:,故选项不符合题意;
,故选项符合题意;
,故选项不符合题意;
不能合并,故选项不符合题意;
故选:.
8.
【分析】求出海里,海里,,再由勾股定理求出的长即可.
【解答】解:如图,一轮船从港口出发以16海里时的速度向北偏东方向航行,另一轮船同时从港口出发以12海里时的速度向南偏东方向航行,航行2小时后,
由题意得:(海里),(海里),,
在中,由勾股定理得:(海里),
即航行2小时后,两船相距40海里,
故选:.
9.
【分析】根据面积可求得大正方形和阴影部分的边长,从而求得空白部分的长;观察可知两块空白部分全等,则可得到一块空白的面积;通过长方形面积公式渴求空白部分的宽,最后求出小正方形的边长即可求出面积.
【解答】解:观察可知,两个空白部分的长相等,宽也相等,
重叠部分也为正方形,
空白部分的面积为,
一个空白长方形面积,
大正方形面积为15,重叠部分面积为1,
大正方形边长,重叠部分边长,
空白部分的长,
设空白部分宽为,可得:,
解得:,
小正方形的边长空白部分的宽阴影部分边长,
小正方形面积,
故选:.
10.
【分析】根据三角形中位线定理,可证明四边形为矩形,并求得长和宽,进而求出矩形的面积.
【解答】解:点、、、分别为,,,的中点,
,(三角形中位线定理),
同理可得,.
,并且,
四边形是平行四边形.
,,
,
.
为矩形.
又.
矩形的面积为.
故答案为:.
二、填空题。
11.
【分析】先根据二次根式的乘法得到原式,然后根据二次根式的性质化简即可.
【解答】解:原式
.
故答案为.
12.
【分析】根据是整数可知,一定是一个完全平方数,即可求解.
【解答】解:是整数,
则一定是一个完全平方数,
,
当时,一个完全平方数.
正整数的最小值为3.
故答案为:3.
13.
【分析】题中没有指明哪个是直角边哪个是斜边,故应该分情况进行分析.
【解答】解:(1)当两边均为直角边时,由勾股定理得,第三边为5
(2)当4为斜边时,由勾股定理得,第三边为
故直角三角形的第三边应该为5或
14.
【分析】连接,由平行线的性质得出,由平行四边形的性质可得出答案.
【解答】解:连接,
,
,
的面积为5,
的面积为5,
四边形为平行四边形,
平行四边形的面积.
故答案为:10.
15.
【分析】根据题意可得,,作,交于点,则,从而即可得到.
【解答】解:当时,面积为,
,
将从扭动到,
,
作,交于点,如图所示,
,
,
故答案为:.
16.
【分析】根据直角三角形斜边上中线性质求出,根据三角形的面积公式求出即可.
【解答】解:中,
为斜边中点,,
,
边上的高,
的面积是.
故答案为:.
三、解答题
17.解:(1)原式
;
(2)原式
.
18.解:(1),,
,,
,
;
(2).
19.(1)证明:,,
四边形是平行四边形,
四边形是矩形,
,
,
四边形是菱形;
(2)解:四边形是矩形,
,
四边形是菱形,,
,,
,
在中,由勾股定理得:,
,,
.
20.证明:,
,,
又点为的中点,
,
在和中,
,
,
,
又四边形是平行四边形,
,
,
又,
四边形是平行四边形.
21.解:(1)在中,,,
,
沿着折叠以后点正好落在点处,
;
(2)在中,,,
,
沿着折叠以后点正好落在点处,
,,
,
设,则,
中,,
,
解得.
即的长为3.
22.解:(1),
故答案为:4;
(2)如图,点,,即为所求;
(3),.
故答案为:或.
23.解:(1)①当点与点重合时,由旋转的性质得:,,
过点作的垂线交的延长线于,则,
四边形为正方形,且边长为4,
,,,
,
,
,
在和中,
,
,
,,
,
在中,,,
由勾股定理得:.
②点在直线上运动,
有以下两种情况:
当点在的延长线上时,设,
过点作的垂线交的延长线于,由旋转的性质得:,,
,,
,,,
,
在和中,
,
,
,,
,
在中,,,,
由勾股定理得:,
即:,
,
或(不合题意,舍去),
.
当点在的延长线上时,
过点作的垂线交的延长线于,由旋转的性质得:,,
,,
,
在和中
,
,
,,
,
在中,,,
由勾股定理得:,
,
.
综上所述:的长度为或.
(2),,其中,
过点作的垂线交的延长线于,过点作的垂线交的延长线于,过点作于,
则,
四边形为矩形,
,,
由旋转的性质得:,,,,
,,
又,,
,,
在和中,
,
,
,,
在和中,
,
,
,,
,,
,
在中,,,,
由勾股定理得:,
即:,其中.
24.解:(1),,
,,
;
(2)设,,则,
,
,
即,
,
,
,
,
.
25.(1)解:四边形是菱形,
,
,
,,
,
,
四边形是平行四边形,
是矩形,
,
设,,
,
,
;
(2)证明:如图1,
证明:延长至,使,连接,
由(1)知:,
,
,
,
,
,
,,
,
,
,
,
,
(3)解:如图2,
设与交于点,
,,,
,
,,
,
,,
,,
,
,
,
,
.
测试范围:二次根式、勾股定理、平行四边形
一、选择题。(共10小题,每小题3分,共30分)
1.使有意义的的取值范围是
A. B. C.x≤2024 D.x≥2024
2.平行四边形的周长为,其中一边长为,则它的邻边长为
A.2 B. C. D.
3.下列二次根式中,不是最简二次根式的是
A. B. C. D.
4.在中,,则
A. B. C. D.
5.下列命题的逆命题是真命题的个数有
①如果两个实数相等,那么它们的绝对值相等;
②全等三角形的对应角相等;
③如果两个角是直角,那么它们相等;
④平行四边形的对角线互相平分;
⑤对顶角相等.
A.0个 B.1个 C.2个 D.3个
6.在中,若,,,则下列条件不能判定是直角三角形的是
A. B.
C.,, D.,
7.下列计算正确的是
A. B. C. D.
8.如图,一轮船从港口出发以16海里时的速度向北偏东方向航行,另一轮船同时从港口出发以12海里时的速度向南偏东方向航行,航行2小时后,两船相距
A.25海里 B.30海里 C.40海里 D.60海里
9.如图,在一个正方形的内部放置大小不同的两个小正方形,其中较大的正方形条的面积为15,重叠部分的面积为1,空白部分的面积为,则较小的正方形面积为
A.4 B. C.9 D.
10.如图,是内部一点,,且,依次取,,,的中点,并顺次连接得到四边形,则四边形的面积是
A. B.12 C.24 D.48
二、填空题。(共6小题,每小题3分,共18分)
11.化简: .
12.已知是整数,则正整数的最小值为 .
13.直角三角形有两边长分别为3,4,则该直角三角形第三边为 .
14.如图,,点、、在直线上,四边形为平行四边形,若的面积为5,则平行四边形的面积是 .
15.如图,平行四边形的活动框架,当时,面积为,将从扭动到,则四边形面积为 .
16.如图,中,为斜边的中点,为斜边上的高,若,,则的面积是 .
三、解答题(共9小题,共72分)
17.计算:
(1); (2).
18.已知:,.求下列各式的值.
(1); (2).
19.如图,矩形的对角线,交于点,延长到点,使,延长到点,使,连接,,.
(1)求证:四边形是菱形;
(2)若,,求菱形的面积.
20.如图,平行四边形的对角线与相交于点,点为的中点,过点作交的延长线于点,连接.求证:四边形是平行四边形.
21.如图,在中,,将沿着折叠以后点正好落在边上的点处.
(1)当时,求的度数;
(2)当,时,求线段的长.
22.如图,是由边长为1的小正方形组成的网格,其中点、、均在网格的格点上.
(1)直接写出格点的面积为 ;
(2)在网格中画出使、、、四点构成平行四边形的所有点;
(3)直接写出线段的长为 .
23.已知正方形的边长为4..
(1)如图1,点在直线上运动,连接,将线段绕点按顺时针旋转得到,连接.
①若点与重合,则 .
②若,求的长.
(2)如图2,点在边上不与,重合)运动,且,连接、.将线段绕点逆时针旋转得到,将线段绕点顺时针旋转得到,设,,求关于的函数表达式.
24.(1)已知,,求的值;
(2)若,求的值.
25.如图,在中,,以为边在外作菱形,对角线交于点,连接,.
(1)如图(1),若,,,请直接写出的长;
(2)如图(2),若,求证;
(3)如图(3),若,请直接写出的值.
答案
一、选择题。
1.
【分析】根据二次根式被开方数不小于零条件进行解题即可.
【解答】解:由题可知,
X-2024≥0,
解得x≥2024.
故选:.
2.
【分析】根据平行四边形对边相等即可解决问题.
【解答】解:因为平行四边形的周长为,其中一边长为,
则它的邻边长为.
故选.
3.
【分析】根据最简二次根式的概念判断即可.
【解答】解:、是最简二次根式,不符合题意;
、是最简二次根式,不符合题意;
、,不是最简二次根式,符合题意;
、是最简二次根式,不符合题意;
故选:.
4.
【分析】根据平行四边形的邻角互补即可得出的度数.
【解答】解:根据平行四边形的性质可得:.
故选:.
5.
【分析】分别写出各个命题的逆命题,根据绝对值的性质、全等三角形的判定、平行四边形的判定、对顶角的概念判断即可.
【解答】解:①如果两个实数相等,那么它们的绝对值相等的逆命题是如果两个实数们的绝对值相等,那么这两个实数相等,是假命题;
②全等三角形的对应角相等的逆命题是对应角相等的三角形全等,是假命题;
③如果两个角是直角,那么它们相等的逆命题是如果两个角相等,那么这两个角是直角,是假命题;
④平行四边形的对角线互相平分的逆命题是对角线互相平分的四边形是平行四边形,是真命题;
⑤对顶角相等的逆命题是相等的角是对顶角,是假命题;
故选:.
6.
【分析】根据勾股定理的逆定理,三角形内角和定理进行计算,逐一判断即可解答.
【解答】解:、,
,
是直角三角形,
故不符合题意;
、,
,
,
,
,
是直角三角形,
故不符合题意;
、,,
,
不是直角三角形,
故符合题意;
、,,
,
是直角三角形,
故不符合题意;
故选:.
7.
【分析】根据二次根式的混合运算法则即可得出答案.
【解答】解:,故选项不符合题意;
,故选项符合题意;
,故选项不符合题意;
不能合并,故选项不符合题意;
故选:.
8.
【分析】求出海里,海里,,再由勾股定理求出的长即可.
【解答】解:如图,一轮船从港口出发以16海里时的速度向北偏东方向航行,另一轮船同时从港口出发以12海里时的速度向南偏东方向航行,航行2小时后,
由题意得:(海里),(海里),,
在中,由勾股定理得:(海里),
即航行2小时后,两船相距40海里,
故选:.
9.
【分析】根据面积可求得大正方形和阴影部分的边长,从而求得空白部分的长;观察可知两块空白部分全等,则可得到一块空白的面积;通过长方形面积公式渴求空白部分的宽,最后求出小正方形的边长即可求出面积.
【解答】解:观察可知,两个空白部分的长相等,宽也相等,
重叠部分也为正方形,
空白部分的面积为,
一个空白长方形面积,
大正方形面积为15,重叠部分面积为1,
大正方形边长,重叠部分边长,
空白部分的长,
设空白部分宽为,可得:,
解得:,
小正方形的边长空白部分的宽阴影部分边长,
小正方形面积,
故选:.
10.
【分析】根据三角形中位线定理,可证明四边形为矩形,并求得长和宽,进而求出矩形的面积.
【解答】解:点、、、分别为,,,的中点,
,(三角形中位线定理),
同理可得,.
,并且,
四边形是平行四边形.
,,
,
.
为矩形.
又.
矩形的面积为.
故答案为:.
二、填空题。
11.
【分析】先根据二次根式的乘法得到原式,然后根据二次根式的性质化简即可.
【解答】解:原式
.
故答案为.
12.
【分析】根据是整数可知,一定是一个完全平方数,即可求解.
【解答】解:是整数,
则一定是一个完全平方数,
,
当时,一个完全平方数.
正整数的最小值为3.
故答案为:3.
13.
【分析】题中没有指明哪个是直角边哪个是斜边,故应该分情况进行分析.
【解答】解:(1)当两边均为直角边时,由勾股定理得,第三边为5
(2)当4为斜边时,由勾股定理得,第三边为
故直角三角形的第三边应该为5或
14.
【分析】连接,由平行线的性质得出,由平行四边形的性质可得出答案.
【解答】解:连接,
,
,
的面积为5,
的面积为5,
四边形为平行四边形,
平行四边形的面积.
故答案为:10.
15.
【分析】根据题意可得,,作,交于点,则,从而即可得到.
【解答】解:当时,面积为,
,
将从扭动到,
,
作,交于点,如图所示,
,
,
故答案为:.
16.
【分析】根据直角三角形斜边上中线性质求出,根据三角形的面积公式求出即可.
【解答】解:中,
为斜边中点,,
,
边上的高,
的面积是.
故答案为:.
三、解答题
17.解:(1)原式
;
(2)原式
.
18.解:(1),,
,,
,
;
(2).
19.(1)证明:,,
四边形是平行四边形,
四边形是矩形,
,
,
四边形是菱形;
(2)解:四边形是矩形,
,
四边形是菱形,,
,,
,
在中,由勾股定理得:,
,,
.
20.证明:,
,,
又点为的中点,
,
在和中,
,
,
,
又四边形是平行四边形,
,
,
又,
四边形是平行四边形.
21.解:(1)在中,,,
,
沿着折叠以后点正好落在点处,
;
(2)在中,,,
,
沿着折叠以后点正好落在点处,
,,
,
设,则,
中,,
,
解得.
即的长为3.
22.解:(1),
故答案为:4;
(2)如图,点,,即为所求;
(3),.
故答案为:或.
23.解:(1)①当点与点重合时,由旋转的性质得:,,
过点作的垂线交的延长线于,则,
四边形为正方形,且边长为4,
,,,
,
,
,
在和中,
,
,
,,
,
在中,,,
由勾股定理得:.
②点在直线上运动,
有以下两种情况:
当点在的延长线上时,设,
过点作的垂线交的延长线于,由旋转的性质得:,,
,,
,,,
,
在和中,
,
,
,,
,
在中,,,,
由勾股定理得:,
即:,
,
或(不合题意,舍去),
.
当点在的延长线上时,
过点作的垂线交的延长线于,由旋转的性质得:,,
,,
,
在和中
,
,
,,
,
在中,,,
由勾股定理得:,
,
.
综上所述:的长度为或.
(2),,其中,
过点作的垂线交的延长线于,过点作的垂线交的延长线于,过点作于,
则,
四边形为矩形,
,,
由旋转的性质得:,,,,
,,
又,,
,,
在和中,
,
,
,,
在和中,
,
,
,,
,,
,
在中,,,,
由勾股定理得:,
即:,其中.
24.解:(1),,
,,
;
(2)设,,则,
,
,
即,
,
,
,
,
.
25.(1)解:四边形是菱形,
,
,
,,
,
,
四边形是平行四边形,
是矩形,
,
设,,
,
,
;
(2)证明:如图1,
证明:延长至,使,连接,
由(1)知:,
,
,
,
,
,
,,
,
,
,
,
,
(3)解:如图2,
设与交于点,
,,,
,
,,
,
,,
,,
,
,
,
,
.
同课章节目录
