人教版七年级数学下册第十章二元一次方程组单元检测卷(含解析)
文档属性
| 名称 | 人教版七年级数学下册第十章二元一次方程组单元检测卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 474.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-06 14:08:38 | ||
图片预览




文档简介
第十章 二元一次方程组(单元检测卷)
一、选择题(每题3分,共24分)
1.下列属于二元一次方程组的是 ( )
A. B. C. D.
2.用代入法解一元二次方程过程中,下列变形不正确的是 ( )
A.由①得 B.由①得
C.由②得 D.由②得
3.二元一次方程有无数个解,下列四组值中是该方程的解的是 ( )
A. B. C. D.
4.已知一个两位数,它的十位上的数字x比个位上的数字y大1,若对调个位与十位上的数字,得到的新数比原数小9,求这个两位数,所列方程组正确的是 ( )
A. B.
C. D.
5.已知关于、的方程组的解满足,则的值为 ( )
A. B. C. D.
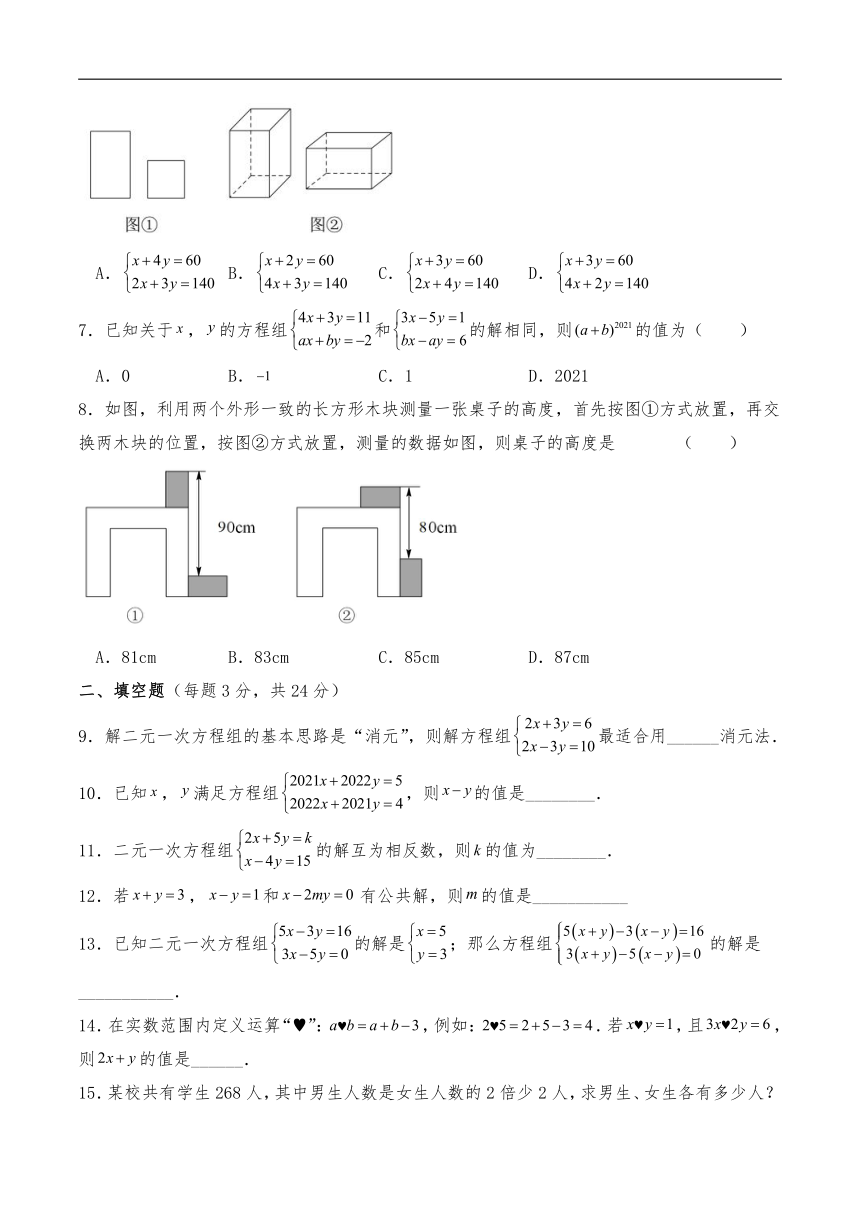
6.用如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒.现有60张正方形纸板和140张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,设做x个竖式无盖纸盒,y个横式无盖纸盒,则可列方程组 ( )
A. B. C. D.
7.已知关于,的方程组和的解相同,则的值为( )
A.0 B. C.1 D.2021
8.如图,利用两个外形一致的长方形木块测量一张桌子的高度,首先按图①方式放置,再交换两木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是 ( )
A.81cm B.83cm C.85cm D.87cm
二、填空题(每题3分,共24分)
9.解二元一次方程组的基本思路是“消元”,则解方程组最适合用______消元法.
10.已知,满足方程组,则的值是________.
11.二元一次方程组的解互为相反数,则的值为________.
12.若,和有公共解,则的值是___________
13.已知二元一次方程组的解是;那么方程组的解是___________.
14.在实数范围内定义运算“ ”:,例如:.若,且,则的值是______.
15.某校共有学生268人,其中男生人数是女生人数的2倍少2人,求男生、女生各有多少人?若设男生有x人,女生有y人,根据题意可列方程组为______________.
16.方程组的解________.
三、解答题(每题8分,共72分)
17.解方程组:
(1); (2).
18.已知关于的方程与有相同的解,求的值及相同的解
19.列二元一次方程组解应用题:某大型超市投入15000元资金购进A、B两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如表所示:
类别/单价 成本价(元/箱) 销售价(元/箱)
A品牌 20 32
B品牌 35 50
(1)该大型超市购进A、B品牌矿泉水各多少箱?
(2)全部销售完600箱矿泉水,该超市共获得多少利润?
20.已知甲种物品每个重,乙种物品每个重,现有甲种物品个,乙种物品个,共重
(1)列出关于的二元一次方程;
(2)若,则
(3)若乙种物品有个,则甲种物品有 个.
21.阅读以下材料:
解方程组:.
小亮在解决这个问题时,发现了一种新的方法,他把这种方法叫做“整体代入法”,解题过程如下:
解:由①得③,将③代入②得:
(1)请你替小亮补全完整的解题过程;
(2)请你用这种方法解方程组:.
22.已知方程组与有相同的解,求
23.在解方程组时,由于粗心,甲看错了方程组中的a,得解为,乙看错了方程组中的b,得解为
(1)甲把a错看成了什么?乙把b错看成了什么?
(2)求出原方程组的解.
24.在平面直角坐标系中,已知点,点(其中为常数,且),则称是点A的“族衍生点”.例如:点的“2族衍生点”的坐标为,即.
(1)点的“3族衍生点”的坐标为 ;
(2)若点A的“5族衍生点”的坐标是,则点A的坐标为 ;
(3)若点(其中,点A的“族衍生点”为点,且,求的值.
25.阅读感悟:
有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:已知实数x、y满足①,②,求和的值.
本题常规思路是将①②两式联立组成方程组,解得x、y的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由①-②可得,由①+②×2可得解得.这样的解题思想就是通常所说的“整体思想”.
解决问题:
(1)已知二元一次方程组则______,______;
(2)某班级组织活动购买小奖品,买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,则购买5支铅笔、5块橡皮、5本日记本共需多少元?
(3)对于实数x、y,定义新运算:解得,其中a、b、c是常数,等式右边是通常的加法和乘法运算,已知,,那么______.
答案
一、选择题
1.
【分析】根据二元一次方程组的定义,逐项判断即可求解.
【解析】解:A、其中一个方程不是整式方程,故不是二元一次方程组,故A不符合题意;
B、有三个未知数,故不是二元一次方程组,故B不符合题意;
C、是二元一次方程组,故C符合题意;
D、是二元二次方程组,故D不符合题意;
故选:C.
2.
【分析】根据代入消元法解方程组的方法,进行变形时要特别注意移项后符号要变号.
【解析】解:
,C选项变形不正确
故选C
3.
【分析】将各项中的x、y的值代入,根据其结果是否等于1即可得解.
【解析】解:把代入方程可得,故不是方程的解;
把代入可得,故是方程的解;
把代入方程可得,故不是方程的解;
把代入可得,故不是方程的解.
故选:B.
4.
【分析】关键描述语是:十位上的数字比个位上的数字大1;新数比原数小9.
等量关系为:①十位上的数字=个位上的数字;②原数=新数.
【解析】解:根据十位上的数字比个位上的数字大1,得方程;
根据对调个位与十位上的数字,得到的新数比原数小9,得方程.
列方程组为.
故选:D.
5.
【分析】将与第二个方程联立,解方程组得到,的值,代入第一个方程,求出即可.
【解析】根据题意得:
解得:
代入中,得
故选:C
6.
【分析】设做x个竖式无盖纸盒,y个横式无盖纸盒,根据60张正方形纸板和140张长方形纸板建立等式.
【解析】解:设做x个竖式无盖纸盒,y个横式无盖纸盒,
根据竖式无盖纸盒用到个正方形纸板和个长方形纸板,横式无盖纸盒用到个正方形纸板和个长方形纸板,
则,
故选:B.
7.
【分析】根据同解方程组的含义可得,求解方程组的解,再代入系数未知的两个方程可得,解方程组得到a,b的值,再代入计算即可.
【解析】解:由题意得: ,
①②得:,
解得:,
把代入①得:,
∴方程组的解为:,
∴ ,
同理解得:,
∴,
故选A.
8.
【分析】设桌子的高度为xcm,长方体木块的长比宽长ycm,观察图①、图②,即可得出关于x、y的二元一次方程组,解之即可得出结论.
【解析】设桌子的高度为xcm,长方体木块的长比宽长ycm,
根据题意得:,
解得:.
故选:C
二、填空题
9.
【分析】根据所给方程组中方程的特点,采用加减消元法合适.
【解析】解:,
①+②得,4x=16,
∴利用加减消元法合适.
故答案为:加减.
10.
【分析】将两式相减即可得出结论.
【解析】解:,
②-①,得:.
故答案为:.
11.
【分析】由题意可得,它与方程组中的第二个方程组成一个新的方程组,先求出的值,再代入方程组中第一个方程,即可求出.
【解析】解:∵关于的二元一次方程组的解互为相反数
解方程组
解得
把代入方程得
故答案为:.
12.
【分析】根据题意:,和有公共解,联立方程组,解出即可得出的值.
【解析】解:∵,和有公共解,
∴可得:,
解得:,
∴的值是.
故答案为:
13.
【分析】观察发现和形式完全相同,故整体考虑,可得,然后解方程即可.
【解析】解:∵和形式完全相同,
∴,解的,
故答案为:
14.
【分析】已知利用题目中的新定义列出关于x,y的二元一次方程组,再求解即可.
【解析】解:∵,且,
∴
由②-①得2x+y=5,
故答案为:5.
15.
【分析】根据“某校共有学生268人,其中男生人数是女生人数的2倍少2人”列出方程组即可.
【解析】解:依题意得:,
故答案为:.
16.
【分析】利用消元法解三元一次方程组即可得.
【解析】解:,
由①②得:④,
由①③得:⑤,
由④⑤得:,
解得,
将代入④得:,
解得,
将,代入③得:,
解得,
则方程组的解为,
故答案为:.
三、解答题
17.
(1)
,
①+②×4得:9x=63,
即x=7,
将x=7代入①得:y=2,
则方程组的解为;
(2)
,
①-②得:3x=-6,
即x=-2,
将x=-2代入①得:y=-2,
则方程组的解为.
18.解:已知:关于x的方程4x k=2与3(2+x)=2k的解相同,
∴ ,
解得 ,
所以k的值为6,相同的解为2.
19.解:(1)设该大型超市购进A品牌矿泉水x箱,B品牌矿泉水y箱,
依题意得:,
解得:.
答:该大型超市购进A品牌矿泉水400箱,B品牌矿泉水200箱.
(2)(元).
答:全部销售完600箱矿泉水,该超市共获得7800元利润.
20.(1)由题意知;
(2)当x=12时,48+7y=76,
解得y=4,
故答案为:4;
(3)当y=8时,4x+56=76,
解得:x=5,即甲种物品有5个,
故答案为:5.
21.(1)解:由①得③,
将③代入②得:,
解得,
将代入③得:,
解得,
∴方程组的解为;
(2)解:,
由①得③,
将③代入②得:,
解得,
将代入③得:,
解得,
∴方程组的解为.
22.解:由题意得:方程组与有相同的解
所以联立得:,
解得:,
代入,
解得:
所以
23.(1)解:将代入方程组可得:,解得,
将代入方程组可得:,解得,
则甲把a错看成了2,乙把b错看成了1;
(2)解:由(1)可得,,代入方程组可得:
,解得
24.(1)解:点的“3族衍生点”的坐标为,即,
故答案为:;
(2)解:设点A坐标为,
由题意可得:,
,
点A坐标为,
故答案为:;
(3)解:点,
点A的“族衍生点”为点,
,
,
,
,
故的值为:.
25.(1)解:
由得:;
由得:.
故答案为:,6.
(2)设铅笔的单价为元,橡皮的单价为元,日记本的单价为元,
依题意得:
由得:.
答:购买5支铅笔、5块橡皮、5本日记本共需30元.
(3)依题意得:
由得:,
即:.
故答案为:.
一、选择题(每题3分,共24分)
1.下列属于二元一次方程组的是 ( )
A. B. C. D.
2.用代入法解一元二次方程过程中,下列变形不正确的是 ( )
A.由①得 B.由①得
C.由②得 D.由②得
3.二元一次方程有无数个解,下列四组值中是该方程的解的是 ( )
A. B. C. D.
4.已知一个两位数,它的十位上的数字x比个位上的数字y大1,若对调个位与十位上的数字,得到的新数比原数小9,求这个两位数,所列方程组正确的是 ( )
A. B.
C. D.
5.已知关于、的方程组的解满足,则的值为 ( )
A. B. C. D.
6.用如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒.现有60张正方形纸板和140张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,设做x个竖式无盖纸盒,y个横式无盖纸盒,则可列方程组 ( )
A. B. C. D.
7.已知关于,的方程组和的解相同,则的值为( )
A.0 B. C.1 D.2021
8.如图,利用两个外形一致的长方形木块测量一张桌子的高度,首先按图①方式放置,再交换两木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是 ( )
A.81cm B.83cm C.85cm D.87cm
二、填空题(每题3分,共24分)
9.解二元一次方程组的基本思路是“消元”,则解方程组最适合用______消元法.
10.已知,满足方程组,则的值是________.
11.二元一次方程组的解互为相反数,则的值为________.
12.若,和有公共解,则的值是___________
13.已知二元一次方程组的解是;那么方程组的解是___________.
14.在实数范围内定义运算“ ”:,例如:.若,且,则的值是______.
15.某校共有学生268人,其中男生人数是女生人数的2倍少2人,求男生、女生各有多少人?若设男生有x人,女生有y人,根据题意可列方程组为______________.
16.方程组的解________.
三、解答题(每题8分,共72分)
17.解方程组:
(1); (2).
18.已知关于的方程与有相同的解,求的值及相同的解
19.列二元一次方程组解应用题:某大型超市投入15000元资金购进A、B两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如表所示:
类别/单价 成本价(元/箱) 销售价(元/箱)
A品牌 20 32
B品牌 35 50
(1)该大型超市购进A、B品牌矿泉水各多少箱?
(2)全部销售完600箱矿泉水,该超市共获得多少利润?
20.已知甲种物品每个重,乙种物品每个重,现有甲种物品个,乙种物品个,共重
(1)列出关于的二元一次方程;
(2)若,则
(3)若乙种物品有个,则甲种物品有 个.
21.阅读以下材料:
解方程组:.
小亮在解决这个问题时,发现了一种新的方法,他把这种方法叫做“整体代入法”,解题过程如下:
解:由①得③,将③代入②得:
(1)请你替小亮补全完整的解题过程;
(2)请你用这种方法解方程组:.
22.已知方程组与有相同的解,求
23.在解方程组时,由于粗心,甲看错了方程组中的a,得解为,乙看错了方程组中的b,得解为
(1)甲把a错看成了什么?乙把b错看成了什么?
(2)求出原方程组的解.
24.在平面直角坐标系中,已知点,点(其中为常数,且),则称是点A的“族衍生点”.例如:点的“2族衍生点”的坐标为,即.
(1)点的“3族衍生点”的坐标为 ;
(2)若点A的“5族衍生点”的坐标是,则点A的坐标为 ;
(3)若点(其中,点A的“族衍生点”为点,且,求的值.
25.阅读感悟:
有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:已知实数x、y满足①,②,求和的值.
本题常规思路是将①②两式联立组成方程组,解得x、y的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由①-②可得,由①+②×2可得解得.这样的解题思想就是通常所说的“整体思想”.
解决问题:
(1)已知二元一次方程组则______,______;
(2)某班级组织活动购买小奖品,买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,则购买5支铅笔、5块橡皮、5本日记本共需多少元?
(3)对于实数x、y,定义新运算:解得,其中a、b、c是常数,等式右边是通常的加法和乘法运算,已知,,那么______.
答案
一、选择题
1.
【分析】根据二元一次方程组的定义,逐项判断即可求解.
【解析】解:A、其中一个方程不是整式方程,故不是二元一次方程组,故A不符合题意;
B、有三个未知数,故不是二元一次方程组,故B不符合题意;
C、是二元一次方程组,故C符合题意;
D、是二元二次方程组,故D不符合题意;
故选:C.
2.
【分析】根据代入消元法解方程组的方法,进行变形时要特别注意移项后符号要变号.
【解析】解:
,C选项变形不正确
故选C
3.
【分析】将各项中的x、y的值代入,根据其结果是否等于1即可得解.
【解析】解:把代入方程可得,故不是方程的解;
把代入可得,故是方程的解;
把代入方程可得,故不是方程的解;
把代入可得,故不是方程的解.
故选:B.
4.
【分析】关键描述语是:十位上的数字比个位上的数字大1;新数比原数小9.
等量关系为:①十位上的数字=个位上的数字;②原数=新数.
【解析】解:根据十位上的数字比个位上的数字大1,得方程;
根据对调个位与十位上的数字,得到的新数比原数小9,得方程.
列方程组为.
故选:D.
5.
【分析】将与第二个方程联立,解方程组得到,的值,代入第一个方程,求出即可.
【解析】根据题意得:
解得:
代入中,得
故选:C
6.
【分析】设做x个竖式无盖纸盒,y个横式无盖纸盒,根据60张正方形纸板和140张长方形纸板建立等式.
【解析】解:设做x个竖式无盖纸盒,y个横式无盖纸盒,
根据竖式无盖纸盒用到个正方形纸板和个长方形纸板,横式无盖纸盒用到个正方形纸板和个长方形纸板,
则,
故选:B.
7.
【分析】根据同解方程组的含义可得,求解方程组的解,再代入系数未知的两个方程可得,解方程组得到a,b的值,再代入计算即可.
【解析】解:由题意得: ,
①②得:,
解得:,
把代入①得:,
∴方程组的解为:,
∴ ,
同理解得:,
∴,
故选A.
8.
【分析】设桌子的高度为xcm,长方体木块的长比宽长ycm,观察图①、图②,即可得出关于x、y的二元一次方程组,解之即可得出结论.
【解析】设桌子的高度为xcm,长方体木块的长比宽长ycm,
根据题意得:,
解得:.
故选:C
二、填空题
9.
【分析】根据所给方程组中方程的特点,采用加减消元法合适.
【解析】解:,
①+②得,4x=16,
∴利用加减消元法合适.
故答案为:加减.
10.
【分析】将两式相减即可得出结论.
【解析】解:,
②-①,得:.
故答案为:.
11.
【分析】由题意可得,它与方程组中的第二个方程组成一个新的方程组,先求出的值,再代入方程组中第一个方程,即可求出.
【解析】解:∵关于的二元一次方程组的解互为相反数
解方程组
解得
把代入方程得
故答案为:.
12.
【分析】根据题意:,和有公共解,联立方程组,解出即可得出的值.
【解析】解:∵,和有公共解,
∴可得:,
解得:,
∴的值是.
故答案为:
13.
【分析】观察发现和形式完全相同,故整体考虑,可得,然后解方程即可.
【解析】解:∵和形式完全相同,
∴,解的,
故答案为:
14.
【分析】已知利用题目中的新定义列出关于x,y的二元一次方程组,再求解即可.
【解析】解:∵,且,
∴
由②-①得2x+y=5,
故答案为:5.
15.
【分析】根据“某校共有学生268人,其中男生人数是女生人数的2倍少2人”列出方程组即可.
【解析】解:依题意得:,
故答案为:.
16.
【分析】利用消元法解三元一次方程组即可得.
【解析】解:,
由①②得:④,
由①③得:⑤,
由④⑤得:,
解得,
将代入④得:,
解得,
将,代入③得:,
解得,
则方程组的解为,
故答案为:.
三、解答题
17.
(1)
,
①+②×4得:9x=63,
即x=7,
将x=7代入①得:y=2,
则方程组的解为;
(2)
,
①-②得:3x=-6,
即x=-2,
将x=-2代入①得:y=-2,
则方程组的解为.
18.解:已知:关于x的方程4x k=2与3(2+x)=2k的解相同,
∴ ,
解得 ,
所以k的值为6,相同的解为2.
19.解:(1)设该大型超市购进A品牌矿泉水x箱,B品牌矿泉水y箱,
依题意得:,
解得:.
答:该大型超市购进A品牌矿泉水400箱,B品牌矿泉水200箱.
(2)(元).
答:全部销售完600箱矿泉水,该超市共获得7800元利润.
20.(1)由题意知;
(2)当x=12时,48+7y=76,
解得y=4,
故答案为:4;
(3)当y=8时,4x+56=76,
解得:x=5,即甲种物品有5个,
故答案为:5.
21.(1)解:由①得③,
将③代入②得:,
解得,
将代入③得:,
解得,
∴方程组的解为;
(2)解:,
由①得③,
将③代入②得:,
解得,
将代入③得:,
解得,
∴方程组的解为.
22.解:由题意得:方程组与有相同的解
所以联立得:,
解得:,
代入,
解得:
所以
23.(1)解:将代入方程组可得:,解得,
将代入方程组可得:,解得,
则甲把a错看成了2,乙把b错看成了1;
(2)解:由(1)可得,,代入方程组可得:
,解得
24.(1)解:点的“3族衍生点”的坐标为,即,
故答案为:;
(2)解:设点A坐标为,
由题意可得:,
,
点A坐标为,
故答案为:;
(3)解:点,
点A的“族衍生点”为点,
,
,
,
,
故的值为:.
25.(1)解:
由得:;
由得:.
故答案为:,6.
(2)设铅笔的单价为元,橡皮的单价为元,日记本的单价为元,
依题意得:
由得:.
答:购买5支铅笔、5块橡皮、5本日记本共需30元.
(3)依题意得:
由得:,
即:.
故答案为:.
同课章节目录
