8.6 一元二次方程的应用 同步练习(含答案)
文档属性
| 名称 | 8.6 一元二次方程的应用 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 353.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-06 11:05:55 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第八章 一元二次方程
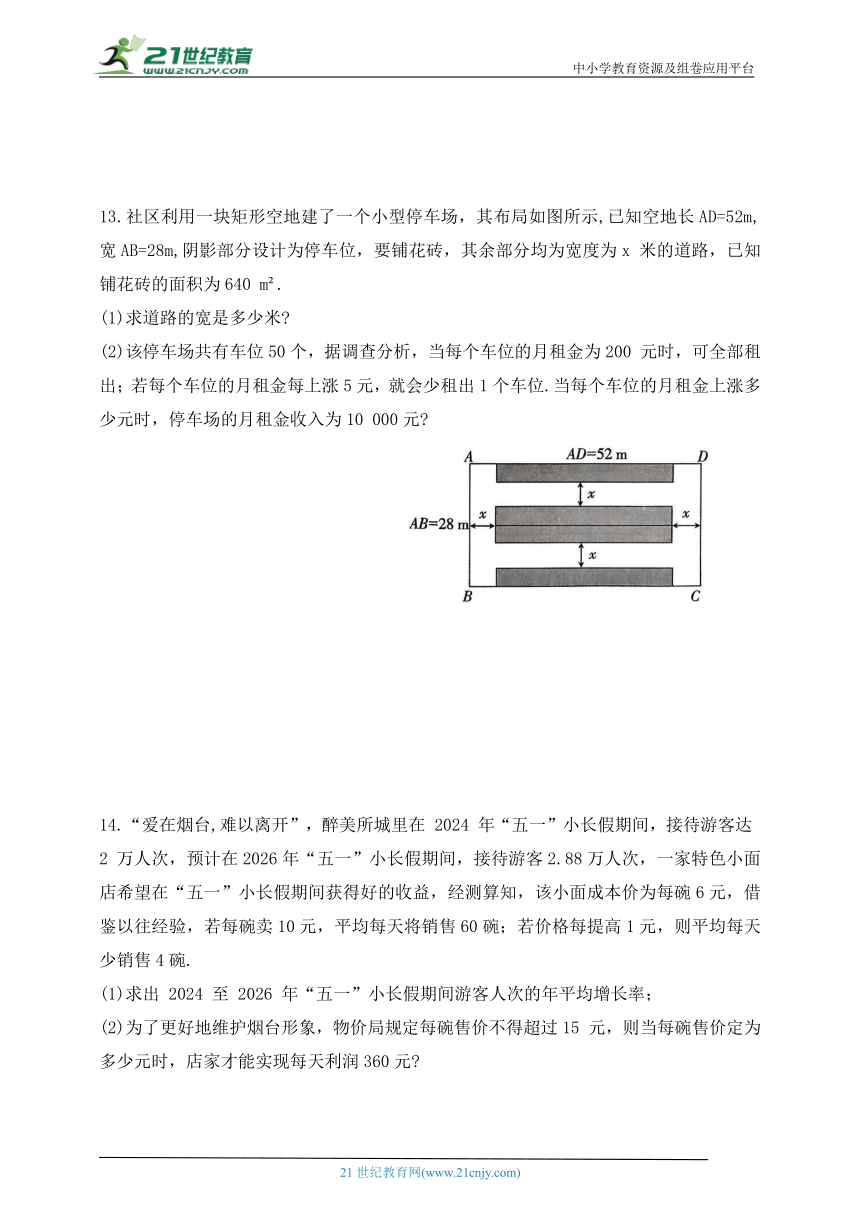
6 一元二次方程的应用
轻松过关
1.如图,在宽 10 米、长22米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为160 平方米.设道路的宽为x米,可列方程( )
2.已知某公司10月份总收入为40万元,经全体员工不懈努力,到12月底实现了第四季度总收入132.4万元的奋斗目标.设11,12两个月总收入的月均增长率为x,由题意可列方程( )
3.黑龙江省中学生排球锦标赛共进行了110场双循环比赛,则参加比赛的队伍共有( )
A.8支 B.9支 C.10支 D.11支
4.在 △ABC 中,∠ABC=90°,AB=6cm,BC=8cm,动点P 从点 A 沿线段 AB 向点 B 移动,一动点Q从点 B 沿线段 BC 向点 C 移动,两点同时开始移动,点 P 的速度为 1 cm/s,点 Q的速度为2cm /s,当Q到达点C 时两点同时停止运动.若使△PBQ的面积为5 cm ,则点 P 运动的时间是 ( )
A.1s B. 4s C.5s 或1 s D.4s 或1s
5.宾馆有 50间房供游客居住,当每间房每天定价为 180 元时,宾馆会住满;当每间房每天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的每间房每天支出 20 元的费用.当房价定为多少元时,宾馆当天的利润为10 890元 设房价比定价 180元增加x元,则有 ( )
6.随着经济复苏,某公司近两年的总收入逐年递增.该公司 2021年缴税 40万元,2023 年缴税 48.4 万元.该公司这两年缴税的年平均增长率是
7.某超市销售一种饮料,平均每天可售出 100 箱,每箱利润 12元,为扩大销量,增加利润,超市准备适当降价,据测算,每箱每降价1元平均每天可多售出20箱,若要使每天销售饮料获利1 440元,则每箱应降价 元.
8.某商场将进价为30元的台灯以单价 40 元售出,平均每月能售出600个.调查表明:这种台灯的单价每上涨1元,其销售量将减少10个.为实现平均每月10 000 元的销售利润,从消费者的角度考虑,商场对这种台灯的售价应定为 元.
9.一个两位数,个位数字比十位数字大2,十位数字2倍的平方恰好等于个位数字与十位数字互换位置的新数,则这个两位数为 .
10.某旅行社的一则广告如下:
我社组团去井冈山红色研学活动,收费标准;如果人数不超过30,那么人均旅游费用为800元;如果人数多于 30,那么每增加1人,人均旅游费用降低10元,但人均旅游费用不得低于500元.
现该旅行社组织了一批学生去井冈山红色研学活动,共计收到费用 28 000 元.设这次旅游共有x人参加,根据题意建立方程为 .
11.如图,在 A Rt△ABC中,∠BAC=30°,BC=5cm ,点 E 从 A 点出发,沿射线 AB 运动,速度为 2cm /s,点 F 从点 C 出发,沿线段 CA 运动,速度为 1 cm/s,连接 EF. E, 第11题图F两点同时出发,当点 F 到达点 A 时,点E也停止运动,请问经过 s后,△AEF的面积恰为12 cm .
12.古算趣题:“笨伯执竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭,有个邻居聪明者,教他斜竿对两角,笨伯依言试一试,不多不少刚抵足,借问竿长多少数,谁人算出我佩服.”其大意是:笨伯拿竹竿进屋,横拿竖拿都进不去,横着比门宽4尺,竖着比门高2尺.他的邻居教他沿着门的对角线斜着拿竿,笨伯一试,刚好进去.问:竹竿有多少尺
13.社区利用一块矩形空地建了一个小型停车场,其布局如图所示,已知空地长AD=52m,宽AB=28m,阴影部分设计为停车位,要铺花砖,其余部分均为宽度为x 米的道路,已知铺花砖的面积为640 m .
(1)求道路的宽是多少米
(2)该停车场共有车位50个,据调查分析,当每个车位的月租金为200 元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为10 000元
14.“爱在烟台,难以离开”,醉美所城里在 2024 年“五一”小长假期间,接待游客达 2 万人次,预计在2026年“五一”小长假期间,接待游客2.88万人次,一家特色小面店希望在“五一”小长假期间获得好的收益,经测算知,该小面成本价为每碗6元,借鉴以往经验,若每碗卖10元,平均每天将销售60碗;若价格每提高1元,则平均每天少销售4碗.
(1)求出 2024 至 2026 年“五一”小长假期间游客人次的年平均增长率;
(2)为了更好地维护烟台形象,物价局规定每碗售价不得超过15 元,则当每碗售价定为多少元时,店家才能实现每天利润360元
15.新高考采用“3+1+2”的模式,对生物学科提出了更高的要求.某学校生物组为培养同学们观察、归纳的能力,组建了生物课外活动小组.在一次野外实践时,同学们发现一种水果黄瓜的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是21.
(1)这种水果黄瓜每个支干长出多少小分支
(2)学校打算建立一块矩形的生物种植田来种植这种水果黄瓜,一面利用学校的墙(墙的最大可用长度为10米),其余部分需要用总长为22米的栅栏围成,且矩形中间需用栅栏隔开,因实验需要,有两个宽为1米的门(门无需栅栏,如图所示).设种植田的宽AB为m 米.若该种植田的面积为36平方米(栅栏的占地面积忽略不计),求该种植田的宽m.
快乐拓展
16.某商场以每件 20 元的价格购进一种商品,经市场调查发现:该商品每天的销售量 y(件)与每件售价x(元)之间满足一次函数关系,其图象如图所示.设该商场销售这种商品每天获利w(元).
(1)求y与x之间的函数关系式;
(2)求ω与x 之间的函数关系式;
(3)该商场规定这种商品每件售价不低于进价且不高于 38元,商品要想获得600元的利润,每件商品的售价应定为多少元
参考答案
1. A 2. D 3. D 4. A 5. C 6.10% 7.3或4 8.50 9.46
10. x[800-10(x-30)]=28000 11.4或6
12.解:设竿长为x尺,
由题意,得 解得
当x=2时,x-2=0,x-4=-2(舍去),∴x=10.
答:竹竿有10尺.
13.解:(1)根据道路的宽为x米,由题意,得(52-2x)(28-2x)=640,
整理,得 解得x =34(舍去),
答:道路的宽为6米;
(2)设月租金上涨a元,停车场月租金收入为10000元,
由题意,得
整理,得 解得a =50,a =0(不合题意,舍去),
答:每个车位的月租金上涨50元时,停车场的月租金收入为10 000元.
14.解:(1)设 2024 至 2026年“五一”小长假期间游客人次的年平均增长率为x,由题意,得
解得 2(不符合题意,舍去).
答:2024 至 2026 年“五一”小长假期间游客人次的年平均增长率为20%;
(2)设每碗售价定为 y元,则每碗的销售利润为(y-6)元,平均每天可销售60-4(y-10)=(100-4y)碗,由题意,得(y-6)(100-4y)=360,
整理,得 解得 y =15,y =16,
又∵每碗售价不得超过15元,∴y=15.
答:当每碗售价定为15元时,店家才能实现每天利润360元.
15.解:(1)设这种水果黄瓜每个支干长出x个小分支,
由题意,得
整理得 解得 (不符合题意,舍去).
答:这种水果黄瓜每个支干长出4个小分支;
(2)∵栅栏的总长为 22 米,且种植田的宽AB为m 米,
∴种植田的长 AD为(22+1×2-3m)米.
由题意,得(22+1×2-3m)·m=36,
整理得 解得m =2,m =6,
当m=2时,22+1×2-3m=22+1×2-3×2=18>10,不符合题意;
当m=6时,22+1×2-3m=22+1×2-3×6=6<10,符合题意.
答:该种植田的宽AB为6米.
16.解:(1)设y与x之间的函数关系式为y= kx+b(k≠0),
由函数图象,得 解得
故y与x的函数关系式为:y=-2x+120;
(2)∵y=-2x+120,∴w=(x-20)y=(x-20)(-2x+120)
即 w 与 x 之间的函数关系式为 w =
(3)由题意,得
∵20≤x≤38,∴x=30.
答:每件商品的售价应定为30元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 一元二次方程
6 一元二次方程的应用
轻松过关
1.如图,在宽 10 米、长22米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为160 平方米.设道路的宽为x米,可列方程( )
2.已知某公司10月份总收入为40万元,经全体员工不懈努力,到12月底实现了第四季度总收入132.4万元的奋斗目标.设11,12两个月总收入的月均增长率为x,由题意可列方程( )
3.黑龙江省中学生排球锦标赛共进行了110场双循环比赛,则参加比赛的队伍共有( )
A.8支 B.9支 C.10支 D.11支
4.在 △ABC 中,∠ABC=90°,AB=6cm,BC=8cm,动点P 从点 A 沿线段 AB 向点 B 移动,一动点Q从点 B 沿线段 BC 向点 C 移动,两点同时开始移动,点 P 的速度为 1 cm/s,点 Q的速度为2cm /s,当Q到达点C 时两点同时停止运动.若使△PBQ的面积为5 cm ,则点 P 运动的时间是 ( )
A.1s B. 4s C.5s 或1 s D.4s 或1s
5.宾馆有 50间房供游客居住,当每间房每天定价为 180 元时,宾馆会住满;当每间房每天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的每间房每天支出 20 元的费用.当房价定为多少元时,宾馆当天的利润为10 890元 设房价比定价 180元增加x元,则有 ( )
6.随着经济复苏,某公司近两年的总收入逐年递增.该公司 2021年缴税 40万元,2023 年缴税 48.4 万元.该公司这两年缴税的年平均增长率是
7.某超市销售一种饮料,平均每天可售出 100 箱,每箱利润 12元,为扩大销量,增加利润,超市准备适当降价,据测算,每箱每降价1元平均每天可多售出20箱,若要使每天销售饮料获利1 440元,则每箱应降价 元.
8.某商场将进价为30元的台灯以单价 40 元售出,平均每月能售出600个.调查表明:这种台灯的单价每上涨1元,其销售量将减少10个.为实现平均每月10 000 元的销售利润,从消费者的角度考虑,商场对这种台灯的售价应定为 元.
9.一个两位数,个位数字比十位数字大2,十位数字2倍的平方恰好等于个位数字与十位数字互换位置的新数,则这个两位数为 .
10.某旅行社的一则广告如下:
我社组团去井冈山红色研学活动,收费标准;如果人数不超过30,那么人均旅游费用为800元;如果人数多于 30,那么每增加1人,人均旅游费用降低10元,但人均旅游费用不得低于500元.
现该旅行社组织了一批学生去井冈山红色研学活动,共计收到费用 28 000 元.设这次旅游共有x人参加,根据题意建立方程为 .
11.如图,在 A Rt△ABC中,∠BAC=30°,BC=5cm ,点 E 从 A 点出发,沿射线 AB 运动,速度为 2cm /s,点 F 从点 C 出发,沿线段 CA 运动,速度为 1 cm/s,连接 EF. E, 第11题图F两点同时出发,当点 F 到达点 A 时,点E也停止运动,请问经过 s后,△AEF的面积恰为12 cm .
12.古算趣题:“笨伯执竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭,有个邻居聪明者,教他斜竿对两角,笨伯依言试一试,不多不少刚抵足,借问竿长多少数,谁人算出我佩服.”其大意是:笨伯拿竹竿进屋,横拿竖拿都进不去,横着比门宽4尺,竖着比门高2尺.他的邻居教他沿着门的对角线斜着拿竿,笨伯一试,刚好进去.问:竹竿有多少尺
13.社区利用一块矩形空地建了一个小型停车场,其布局如图所示,已知空地长AD=52m,宽AB=28m,阴影部分设计为停车位,要铺花砖,其余部分均为宽度为x 米的道路,已知铺花砖的面积为640 m .
(1)求道路的宽是多少米
(2)该停车场共有车位50个,据调查分析,当每个车位的月租金为200 元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为10 000元
14.“爱在烟台,难以离开”,醉美所城里在 2024 年“五一”小长假期间,接待游客达 2 万人次,预计在2026年“五一”小长假期间,接待游客2.88万人次,一家特色小面店希望在“五一”小长假期间获得好的收益,经测算知,该小面成本价为每碗6元,借鉴以往经验,若每碗卖10元,平均每天将销售60碗;若价格每提高1元,则平均每天少销售4碗.
(1)求出 2024 至 2026 年“五一”小长假期间游客人次的年平均增长率;
(2)为了更好地维护烟台形象,物价局规定每碗售价不得超过15 元,则当每碗售价定为多少元时,店家才能实现每天利润360元
15.新高考采用“3+1+2”的模式,对生物学科提出了更高的要求.某学校生物组为培养同学们观察、归纳的能力,组建了生物课外活动小组.在一次野外实践时,同学们发现一种水果黄瓜的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是21.
(1)这种水果黄瓜每个支干长出多少小分支
(2)学校打算建立一块矩形的生物种植田来种植这种水果黄瓜,一面利用学校的墙(墙的最大可用长度为10米),其余部分需要用总长为22米的栅栏围成,且矩形中间需用栅栏隔开,因实验需要,有两个宽为1米的门(门无需栅栏,如图所示).设种植田的宽AB为m 米.若该种植田的面积为36平方米(栅栏的占地面积忽略不计),求该种植田的宽m.
快乐拓展
16.某商场以每件 20 元的价格购进一种商品,经市场调查发现:该商品每天的销售量 y(件)与每件售价x(元)之间满足一次函数关系,其图象如图所示.设该商场销售这种商品每天获利w(元).
(1)求y与x之间的函数关系式;
(2)求ω与x 之间的函数关系式;
(3)该商场规定这种商品每件售价不低于进价且不高于 38元,商品要想获得600元的利润,每件商品的售价应定为多少元
参考答案
1. A 2. D 3. D 4. A 5. C 6.10% 7.3或4 8.50 9.46
10. x[800-10(x-30)]=28000 11.4或6
12.解:设竿长为x尺,
由题意,得 解得
当x=2时,x-2=0,x-4=-2(舍去),∴x=10.
答:竹竿有10尺.
13.解:(1)根据道路的宽为x米,由题意,得(52-2x)(28-2x)=640,
整理,得 解得x =34(舍去),
答:道路的宽为6米;
(2)设月租金上涨a元,停车场月租金收入为10000元,
由题意,得
整理,得 解得a =50,a =0(不合题意,舍去),
答:每个车位的月租金上涨50元时,停车场的月租金收入为10 000元.
14.解:(1)设 2024 至 2026年“五一”小长假期间游客人次的年平均增长率为x,由题意,得
解得 2(不符合题意,舍去).
答:2024 至 2026 年“五一”小长假期间游客人次的年平均增长率为20%;
(2)设每碗售价定为 y元,则每碗的销售利润为(y-6)元,平均每天可销售60-4(y-10)=(100-4y)碗,由题意,得(y-6)(100-4y)=360,
整理,得 解得 y =15,y =16,
又∵每碗售价不得超过15元,∴y=15.
答:当每碗售价定为15元时,店家才能实现每天利润360元.
15.解:(1)设这种水果黄瓜每个支干长出x个小分支,
由题意,得
整理得 解得 (不符合题意,舍去).
答:这种水果黄瓜每个支干长出4个小分支;
(2)∵栅栏的总长为 22 米,且种植田的宽AB为m 米,
∴种植田的长 AD为(22+1×2-3m)米.
由题意,得(22+1×2-3m)·m=36,
整理得 解得m =2,m =6,
当m=2时,22+1×2-3m=22+1×2-3×2=18>10,不符合题意;
当m=6时,22+1×2-3m=22+1×2-3×6=6<10,符合题意.
答:该种植田的宽AB为6米.
16.解:(1)设y与x之间的函数关系式为y= kx+b(k≠0),
由函数图象,得 解得
故y与x的函数关系式为:y=-2x+120;
(2)∵y=-2x+120,∴w=(x-20)y=(x-20)(-2x+120)
即 w 与 x 之间的函数关系式为 w =
(3)由题意,得
∵20≤x≤38,∴x=30.
答:每件商品的售价应定为30元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
