鲁教版八年级下学期期中综合测试卷(含答案)
文档属性
| 名称 | 鲁教版八年级下学期期中综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 441.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-06 11:29:47 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期中综合测试卷
时间: 120分钟 满分: 120分
一、选择题(本题共12个小题,每小题均给出标号为A,B,C,D的四个备选答案,其中只有一个是正确的,每小题3分,共36分)
1.使得式子 有意义的x的取值范围是 ( )
2.下列各组线段中,是成比例线段的一组是 ( )
A.2,3,4,6 B.2,3,4,5 C.2,3,5,7 D.3,4,5,6
3.下列计算中,正确的是 ( )
4.下列二次根式中,最简二次根式是 ( )
5.在复习特殊的平行四边形时,某小组同学画出了如下关系图,组内一名同学在箭头处填写了它们之间转换的条件,其中填写错误的是 ( )
A.①有一个角是直角 B.③有一组邻边相等
C.②对角线互相垂直 D.④对角线互相平分
第5题图 第6题图
6.如图,菱形ABCD中,对角线AC,BD 相交于点O, 点P 和点E 分别为BD,CD上的动点,求 的最小值 ( )
A.14.4 B.16 C.17 D.18.6
7.关于x的一元二次方程有实数根,则实数k的取值范围是( )
8.已知实数x,y满足 则以x,y的值为两边长的等腰三角形的周长是 ( )
A.20或16 B.20 C.16 D.以上答案均不对
9.已知m是方程的一个根,则的值为( )
A. -2 B. 4 C. 1 D. -5
10.如图,在 中, D,F分别是AB,BC的中点, 于点E,连接AF,DF,DE,EF.若BC=6,△DEF的周长是11,则AF的长为 ( )
D.8
11.一种药品原价每盒48元,经过两次降价后每盒27元,两次降价的百分率相同,则每次降价的百分率为 ( )
A. 20% B. 22% C. 25% D. 28%
12.如图,在正方形ABCD中,E是对角线AC上的动点,以DE为边作正方形DEFG,M是CD的中点,连接GM,若正方形 ABCD的边长为8,则GM的最小值为( )
A. 2 D. 4
二、填空题(本题共8个小题,每小题3分,共24分)
13.如图,在四边形ABCD中, 10,DC=4,折叠四边形ABCD,使点 D 与点 B 重合,得到折痕AE,则 CE 的长为 .
14.已知m,n是一元二次方程 的两个不相等的实数根,则
15.已知 则x的值为 .
16.如图,四边形ABCD的两条对角线AC,BD互相垂直, 是四边形ABCD 各边的中点,如果 10,那么四边形, 的面积为 .
17.如图,将矩形 ABCD 绕点B 顺时针旋转 至矩形EBGF 的位置,连接AC,EG,取AC,EG的中点M,N,连接MN,若 则
18.已知 则
19.如图,某小区要在长为16 m,宽为12m的矩形空地上建造一个花坛,使花坛四周小路的宽度相等,且花坛所占面积为空地面积的一半,则小路宽为 m.
第19题图 第20题图
20.如图,直线 与y轴交于点 依次作正方形 正方形 ··正方形 使得点 在直线 上,点 在x轴上,则点 的坐标是 .
三、解答题(本大题共8个小题,要写出必要的解答过程或推理步骤,共60分)
21.(6分)[2024春·青岛期中]解方程;
配方法);
(公式法);
22.(6分)计算:
(2)先化简,再求值: 其中
23.(6分)【问题背景】
已知 求 的值.
【问题解决】
(1)小颖通过思考,形成如下解题思路:先将等式两边都除以x,得到 的值,再利用完全平方公式求出 的值.请按照该思路,写出上述题目完整的求解过程;
【拓展应用】
(2)已知 求 的值;
(3)已知 求 的值.
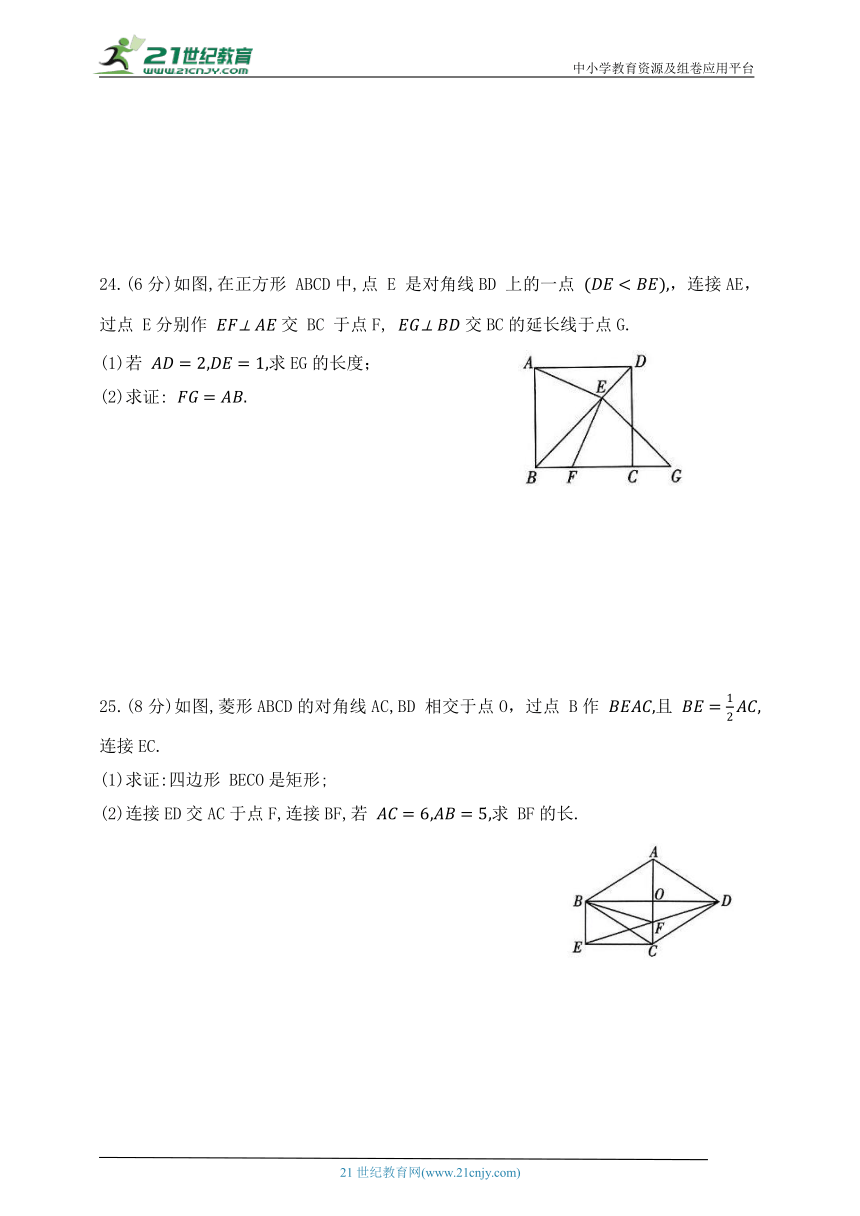
24.(6分)如图,在正方形 ABCD中,点 E 是对角线BD 上的一点 ,连接AE,过点 E分别作 交 BC 于点F, 交BC的延长线于点G.
(1)若 求EG的长度;
(2)求证:
25.(8分)如图,菱形ABCD的对角线AC,BD 相交于点O,过点 B作 且 连接EC.
(1)求证:四边形 BECO是矩形;
(2)连接ED交AC于点F,连接BF,若 求 BF的长.
26.(8分)阅读材料,解答下列问题.
材料:已知 求 的值.
小明同学是这样解答的:
这种方法称为“构造对偶式”.
问题:已知
(1)求 的值;
(2)求x的值.
27.(10分)阅读以下信息,探索完成任务.
素材1 “乐学雷锋好榜样,爱心义卖暖人心”,某中学每月举行义卖活动,同学们用自己的手工制作表达爱心,随着同学们的技术变得娴熟,该手工作品9月份生产100个,11月份生产144个.
素材2 该手工作品的生产成本为30元/个,义卖一段时间后发现,当义卖价格为40 元/个时,月销售量为 600个,若在此基础上义卖价格每上涨1元,则月销售量将减少10个.
问题解决
任务 1 求手工作品9月份到11月份生产数量的平均增长率;
任务 2 若该月捐出善款(去除成本后)10 000元,而且尽可能让更多的人能够献出爱心,请问该手工作品应该定价为多少元
28.(10分)【问题初探】
(1)如图 1a,正方形 ABCD 的边长为2,∠EOF 的顶点O 在正方形ABCD 两条对角线的交点处,∠EOF=90°,将∠EOF 绕点O 旋转,∠EOF 的两边分别与正方形ABCD 的边 BC 和CD 交于点E 和点 F(点F 与点C,D不重合),问:在旋转过程中,四边形OECF的面积会发生变化吗 证明你的结论.
爱思考的小明给出这样的解题思路:如图1b,考虑到正方形对角线的特征,过点O分别作OG⊥BC于点G,OH⊥CD 于点 H,证明△OGE≌△OHF,从而将四边形OECF 的面积转化成了小正方形OGCH 的面积.通过小明的思路点拨,你认为:(填一个数值);
【类比探究】
(2)如图2,在矩形ABCD中,AB=2,AD=4,点O是AD边的中点,∠EOF=90°,点E在AB 上,点 F在BC上,则四边形EBFO的面积为 ,EB+BF= ;
【问题解决】
(3)如图3,有一个菱形菜园 ABCD,AC,BD 为人行步道,且交于点 O.现要在菜园的右下角建一四边形储藏间OECF.已知点 E在BC 上,点F在CD上,∠ABC=∠EOF=60°.若四边形储藏间OECF 的占地面积为 (人行步道的面积忽略不计),要在菱形菜园ABCD围一圈篱笆,则需要篱笆多少米
参考答案
1. B 2. A 3. B 4. B 5. D 6. A 7. B 8. B 9. C 10. B 11. C
12.C 解析:连接CG并延长,与 AD的延长线交于点 K,过点M作MT⊥CK于点T,如图所示:
∵四边形ABCD和四边形DEFG 均为正方形,
∴ AD = CD, DE = DG, ∠ADC = 90°,∠EDG=90°,∠DAC=45°,
∴ ∠ADE + ∠EDC = 90°, ∠CDG +∠EDC=90°,∴∠ADE=∠CDG,
在△ADE和△CDG中, ∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAC=∠DCG=45°,
∴当点 E与点A 重合时,点G与点C重合,当点 E与点C 重合时,点G与点K 重合,即当点 E在线段AC 上运动时,点G在线段CK 上运动,
根据“垂线段最短”,得当 MG⊥CK 时,MG为最短,即当点 G 与点 T 重合时,MG为最小,最小值为线段 MT的长.
∵∠DCK=45°,MT⊥CK,∴△CMT 为等腰直角三角形,即 MT=CT,
∵AB=8,点 M为CD 的中点,∴MC=4,
由勾股定理,得
∴GM的最小值为2
13. 14.2024 15.3 16.20 17.5 18.4 19.2 20.(63,32)
21.解:
或 解得
∴x-3=4或x-3=-4,解得
这里a=3,b=2,c=-2,
∴b -4ac=2 -4×3×(-2)=4+24=28,
∴2(x-2) -(x+2)(x-2)=0,∴(x-2)[2(x-2)-(x+2)]=0,
∴(x-2)(x-6)=0,∴x-2=0或x-6=0,解得x =2,x =6.
22.解:(1)原式
(2)原式 =3m-2,
当 时,原式
23.解:
的值为
的值为
的值为±1.
24.解:(1)∵四边形ABCD 是正方形,∠ABD=∠CBD=45°,
∵EG⊥BD,∠DBG=45°,∴∠DBG=∠EGB=45°,
(2)证明:∵AE⊥EF,EG⊥BE,∴∠AEF=∠BEG=90°,∴∠AEB=∠GEF,
又∵BE=EG,∠ABD=∠FGE=45°,∴△ABE≌△FGE(ASA),∴FG=AB.
25.解:(1)证明:∵四边形ABCD是菱形,∴∠BOC=90°,OC=OA= AC,
∴BE=OC,
∵BE∥AC,∴四边形 BECO是平行四边形,
∵∠BOC=90°,∴平行四边形 BECO是矩形;
(2)∵四边形ABCD是菱形, AC⊥BD,
在 Rt△OBC中,由勾股定理,得∴BD=2OB=8,
由(1),得四边形 BECO 是矩形,∴BE=OC=3,∠OBE=∠ECO=90°,OB=CE,OB∥CE,
∠ODF=∠CEF,OD=CE,
∵∠DOF=∠ECF=90°,∴△ODF≌△CEF(ASA),∴DF=EF,
∵∠DBE=90°,
26.解:(1)·
(2)由(1),得2,
∴9+x=6.25,∴x=-2.75.
27.解:任务1.设手工作品 9 月份到 11月份生产数量的平均增长率为x,
由题意,得100(1+x) =144,解得x =0.2 =20%,x =-2.2(舍去),
答:手工作品 9 月份到11月份生产数量的平均增长率为20%;
任务2.设该手工作品应该定价为m元,
由题意得(m-30)[600-10(m-40)]=10000,整理得 解得m=50或m=80.
∵要尽可能让更多的人能够献出爱心,∴m=50.
答:该手工作品应该定价为50元.
28.解:(1)∵OG⊥BC,OH⊥CD,∴∠OGC=∠OHC=90°,
∵∠BCD=90°,∴四边形OGCH 是矩形,∴∠GOH=90°,
∵∠EOF=90°,∴∠GOE=∠HOF,
∵四边形 ABCD是正方形,边长为2,∴AB=AD=2,OA=OB=OC=OD,
∵OG⊥BC,∴BG=CG=1,∴OG是△ABC的中位线,
同理,得 ∴OG=OH=1,
∴△OGE≌△OHF(ASA),四边形 OGCH是正方形,∴EG=FH,S△OGE=S△OHF,
∴S四边形OECF = S△OEC + S△OCF = S△OEC + S正方形OGCH
故答案为:1;
(2)如图2,过点O作OM⊥BC于点M,
则∠OMB=∠OMF=90°,
∵四边形 ABCD 是矩形,∴∠A=∠B=90°,∴四边形ABMO是矩形,
∴OM=AB=2,BM=OA,∠AOM=90°,
∵AD=4,点O是AD边的中点,∴BM=OA=2,∴OA=OM=2,∴四边形ABMO是正方形,
∵∠EOF=90°,∴∠AOE=∠MOF,
∵OA=OM,∠A=∠OMF=90°,∴△AOE≌△MOF(ASA),∴S△AOE=S△MOF,AE=MF,
∴S四边形EBFO =S四边形ABMO =4,EB+BF=AB-AE+BM+MF=AB+BM=2+2=4,
故答案为:4,4;
(3)如图3,过点O作ON∥BC交CD 于点N,
∵ 四边 形 ABCD 是菱 形,∠ABC =∠EOF=60°,则∠BCD=120°,
∴AB=BC=CD,OA=OC,OB=OD,AC⊥
∴△ABC是等边三角形,设其边长为a,∴AC=AB=a,OA=OC= a,
∵ON∥BC,∴∠NOC=∠ACB=60°,∠ONC=180°-∠BCD=60°,
∴∠NOC=∠ACD=∠ONC=60°,∴△OCN 是等边三角形,
∴∠EOC=∠NOF,
∵∠ONF=∠OCE=60°,∴△OCE≌△ONF(ASA),∴S△OCE=S△ONF,
∴S四边形OECF
∵四边形储藏间 OECF 的占地面积为
解得a=8(负值舍去),即AB=8,
∴菱形的周长为4×8=32.
答:需要篱笆32 m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中综合测试卷
时间: 120分钟 满分: 120分
一、选择题(本题共12个小题,每小题均给出标号为A,B,C,D的四个备选答案,其中只有一个是正确的,每小题3分,共36分)
1.使得式子 有意义的x的取值范围是 ( )
2.下列各组线段中,是成比例线段的一组是 ( )
A.2,3,4,6 B.2,3,4,5 C.2,3,5,7 D.3,4,5,6
3.下列计算中,正确的是 ( )
4.下列二次根式中,最简二次根式是 ( )
5.在复习特殊的平行四边形时,某小组同学画出了如下关系图,组内一名同学在箭头处填写了它们之间转换的条件,其中填写错误的是 ( )
A.①有一个角是直角 B.③有一组邻边相等
C.②对角线互相垂直 D.④对角线互相平分
第5题图 第6题图
6.如图,菱形ABCD中,对角线AC,BD 相交于点O, 点P 和点E 分别为BD,CD上的动点,求 的最小值 ( )
A.14.4 B.16 C.17 D.18.6
7.关于x的一元二次方程有实数根,则实数k的取值范围是( )
8.已知实数x,y满足 则以x,y的值为两边长的等腰三角形的周长是 ( )
A.20或16 B.20 C.16 D.以上答案均不对
9.已知m是方程的一个根,则的值为( )
A. -2 B. 4 C. 1 D. -5
10.如图,在 中, D,F分别是AB,BC的中点, 于点E,连接AF,DF,DE,EF.若BC=6,△DEF的周长是11,则AF的长为 ( )
D.8
11.一种药品原价每盒48元,经过两次降价后每盒27元,两次降价的百分率相同,则每次降价的百分率为 ( )
A. 20% B. 22% C. 25% D. 28%
12.如图,在正方形ABCD中,E是对角线AC上的动点,以DE为边作正方形DEFG,M是CD的中点,连接GM,若正方形 ABCD的边长为8,则GM的最小值为( )
A. 2 D. 4
二、填空题(本题共8个小题,每小题3分,共24分)
13.如图,在四边形ABCD中, 10,DC=4,折叠四边形ABCD,使点 D 与点 B 重合,得到折痕AE,则 CE 的长为 .
14.已知m,n是一元二次方程 的两个不相等的实数根,则
15.已知 则x的值为 .
16.如图,四边形ABCD的两条对角线AC,BD互相垂直, 是四边形ABCD 各边的中点,如果 10,那么四边形, 的面积为 .
17.如图,将矩形 ABCD 绕点B 顺时针旋转 至矩形EBGF 的位置,连接AC,EG,取AC,EG的中点M,N,连接MN,若 则
18.已知 则
19.如图,某小区要在长为16 m,宽为12m的矩形空地上建造一个花坛,使花坛四周小路的宽度相等,且花坛所占面积为空地面积的一半,则小路宽为 m.
第19题图 第20题图
20.如图,直线 与y轴交于点 依次作正方形 正方形 ··正方形 使得点 在直线 上,点 在x轴上,则点 的坐标是 .
三、解答题(本大题共8个小题,要写出必要的解答过程或推理步骤,共60分)
21.(6分)[2024春·青岛期中]解方程;
配方法);
(公式法);
22.(6分)计算:
(2)先化简,再求值: 其中
23.(6分)【问题背景】
已知 求 的值.
【问题解决】
(1)小颖通过思考,形成如下解题思路:先将等式两边都除以x,得到 的值,再利用完全平方公式求出 的值.请按照该思路,写出上述题目完整的求解过程;
【拓展应用】
(2)已知 求 的值;
(3)已知 求 的值.
24.(6分)如图,在正方形 ABCD中,点 E 是对角线BD 上的一点 ,连接AE,过点 E分别作 交 BC 于点F, 交BC的延长线于点G.
(1)若 求EG的长度;
(2)求证:
25.(8分)如图,菱形ABCD的对角线AC,BD 相交于点O,过点 B作 且 连接EC.
(1)求证:四边形 BECO是矩形;
(2)连接ED交AC于点F,连接BF,若 求 BF的长.
26.(8分)阅读材料,解答下列问题.
材料:已知 求 的值.
小明同学是这样解答的:
这种方法称为“构造对偶式”.
问题:已知
(1)求 的值;
(2)求x的值.
27.(10分)阅读以下信息,探索完成任务.
素材1 “乐学雷锋好榜样,爱心义卖暖人心”,某中学每月举行义卖活动,同学们用自己的手工制作表达爱心,随着同学们的技术变得娴熟,该手工作品9月份生产100个,11月份生产144个.
素材2 该手工作品的生产成本为30元/个,义卖一段时间后发现,当义卖价格为40 元/个时,月销售量为 600个,若在此基础上义卖价格每上涨1元,则月销售量将减少10个.
问题解决
任务 1 求手工作品9月份到11月份生产数量的平均增长率;
任务 2 若该月捐出善款(去除成本后)10 000元,而且尽可能让更多的人能够献出爱心,请问该手工作品应该定价为多少元
28.(10分)【问题初探】
(1)如图 1a,正方形 ABCD 的边长为2,∠EOF 的顶点O 在正方形ABCD 两条对角线的交点处,∠EOF=90°,将∠EOF 绕点O 旋转,∠EOF 的两边分别与正方形ABCD 的边 BC 和CD 交于点E 和点 F(点F 与点C,D不重合),问:在旋转过程中,四边形OECF的面积会发生变化吗 证明你的结论.
爱思考的小明给出这样的解题思路:如图1b,考虑到正方形对角线的特征,过点O分别作OG⊥BC于点G,OH⊥CD 于点 H,证明△OGE≌△OHF,从而将四边形OECF 的面积转化成了小正方形OGCH 的面积.通过小明的思路点拨,你认为:(填一个数值);
【类比探究】
(2)如图2,在矩形ABCD中,AB=2,AD=4,点O是AD边的中点,∠EOF=90°,点E在AB 上,点 F在BC上,则四边形EBFO的面积为 ,EB+BF= ;
【问题解决】
(3)如图3,有一个菱形菜园 ABCD,AC,BD 为人行步道,且交于点 O.现要在菜园的右下角建一四边形储藏间OECF.已知点 E在BC 上,点F在CD上,∠ABC=∠EOF=60°.若四边形储藏间OECF 的占地面积为 (人行步道的面积忽略不计),要在菱形菜园ABCD围一圈篱笆,则需要篱笆多少米
参考答案
1. B 2. A 3. B 4. B 5. D 6. A 7. B 8. B 9. C 10. B 11. C
12.C 解析:连接CG并延长,与 AD的延长线交于点 K,过点M作MT⊥CK于点T,如图所示:
∵四边形ABCD和四边形DEFG 均为正方形,
∴ AD = CD, DE = DG, ∠ADC = 90°,∠EDG=90°,∠DAC=45°,
∴ ∠ADE + ∠EDC = 90°, ∠CDG +∠EDC=90°,∴∠ADE=∠CDG,
在△ADE和△CDG中, ∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAC=∠DCG=45°,
∴当点 E与点A 重合时,点G与点C重合,当点 E与点C 重合时,点G与点K 重合,即当点 E在线段AC 上运动时,点G在线段CK 上运动,
根据“垂线段最短”,得当 MG⊥CK 时,MG为最短,即当点 G 与点 T 重合时,MG为最小,最小值为线段 MT的长.
∵∠DCK=45°,MT⊥CK,∴△CMT 为等腰直角三角形,即 MT=CT,
∵AB=8,点 M为CD 的中点,∴MC=4,
由勾股定理,得
∴GM的最小值为2
13. 14.2024 15.3 16.20 17.5 18.4 19.2 20.(63,32)
21.解:
或 解得
∴x-3=4或x-3=-4,解得
这里a=3,b=2,c=-2,
∴b -4ac=2 -4×3×(-2)=4+24=28,
∴2(x-2) -(x+2)(x-2)=0,∴(x-2)[2(x-2)-(x+2)]=0,
∴(x-2)(x-6)=0,∴x-2=0或x-6=0,解得x =2,x =6.
22.解:(1)原式
(2)原式 =3m-2,
当 时,原式
23.解:
的值为
的值为
的值为±1.
24.解:(1)∵四边形ABCD 是正方形,∠ABD=∠CBD=45°,
∵EG⊥BD,∠DBG=45°,∴∠DBG=∠EGB=45°,
(2)证明:∵AE⊥EF,EG⊥BE,∴∠AEF=∠BEG=90°,∴∠AEB=∠GEF,
又∵BE=EG,∠ABD=∠FGE=45°,∴△ABE≌△FGE(ASA),∴FG=AB.
25.解:(1)证明:∵四边形ABCD是菱形,∴∠BOC=90°,OC=OA= AC,
∴BE=OC,
∵BE∥AC,∴四边形 BECO是平行四边形,
∵∠BOC=90°,∴平行四边形 BECO是矩形;
(2)∵四边形ABCD是菱形, AC⊥BD,
在 Rt△OBC中,由勾股定理,得∴BD=2OB=8,
由(1),得四边形 BECO 是矩形,∴BE=OC=3,∠OBE=∠ECO=90°,OB=CE,OB∥CE,
∠ODF=∠CEF,OD=CE,
∵∠DOF=∠ECF=90°,∴△ODF≌△CEF(ASA),∴DF=EF,
∵∠DBE=90°,
26.解:(1)·
(2)由(1),得2,
∴9+x=6.25,∴x=-2.75.
27.解:任务1.设手工作品 9 月份到 11月份生产数量的平均增长率为x,
由题意,得100(1+x) =144,解得x =0.2 =20%,x =-2.2(舍去),
答:手工作品 9 月份到11月份生产数量的平均增长率为20%;
任务2.设该手工作品应该定价为m元,
由题意得(m-30)[600-10(m-40)]=10000,整理得 解得m=50或m=80.
∵要尽可能让更多的人能够献出爱心,∴m=50.
答:该手工作品应该定价为50元.
28.解:(1)∵OG⊥BC,OH⊥CD,∴∠OGC=∠OHC=90°,
∵∠BCD=90°,∴四边形OGCH 是矩形,∴∠GOH=90°,
∵∠EOF=90°,∴∠GOE=∠HOF,
∵四边形 ABCD是正方形,边长为2,∴AB=AD=2,OA=OB=OC=OD,
∵OG⊥BC,∴BG=CG=1,∴OG是△ABC的中位线,
同理,得 ∴OG=OH=1,
∴△OGE≌△OHF(ASA),四边形 OGCH是正方形,∴EG=FH,S△OGE=S△OHF,
∴S四边形OECF = S△OEC + S△OCF = S△OEC + S正方形OGCH
故答案为:1;
(2)如图2,过点O作OM⊥BC于点M,
则∠OMB=∠OMF=90°,
∵四边形 ABCD 是矩形,∴∠A=∠B=90°,∴四边形ABMO是矩形,
∴OM=AB=2,BM=OA,∠AOM=90°,
∵AD=4,点O是AD边的中点,∴BM=OA=2,∴OA=OM=2,∴四边形ABMO是正方形,
∵∠EOF=90°,∴∠AOE=∠MOF,
∵OA=OM,∠A=∠OMF=90°,∴△AOE≌△MOF(ASA),∴S△AOE=S△MOF,AE=MF,
∴S四边形EBFO =S四边形ABMO =4,EB+BF=AB-AE+BM+MF=AB+BM=2+2=4,
故答案为:4,4;
(3)如图3,过点O作ON∥BC交CD 于点N,
∵ 四边 形 ABCD 是菱 形,∠ABC =∠EOF=60°,则∠BCD=120°,
∴AB=BC=CD,OA=OC,OB=OD,AC⊥
∴△ABC是等边三角形,设其边长为a,∴AC=AB=a,OA=OC= a,
∵ON∥BC,∴∠NOC=∠ACB=60°,∠ONC=180°-∠BCD=60°,
∴∠NOC=∠ACD=∠ONC=60°,∴△OCN 是等边三角形,
∴∠EOC=∠NOF,
∵∠ONF=∠OCE=60°,∴△OCE≌△ONF(ASA),∴S△OCE=S△ONF,
∴S四边形OECF
∵四边形储藏间 OECF 的占地面积为
解得a=8(负值舍去),即AB=8,
∴菱形的周长为4×8=32.
答:需要篱笆32 m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
