北师大版八下1.1.1 等腰三角形(1) 课件
文档属性
| 名称 | 北师大版八下1.1.1 等腰三角形(1) 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-06 17:47:33 | ||
图片预览








文档简介
(共26张PPT)
第一章 三角形的证明
1.1.1 等腰三角形(1)
北师大版 数学 八年级 下册
学习目标
1、经历“探索-发现-猜想-证明”的过程证明等腰三角形的有关性质,并能运用性质定理去解决实际问题;
2、在证明的过程中发现数学证明的要求和步骤,体会证明思想.
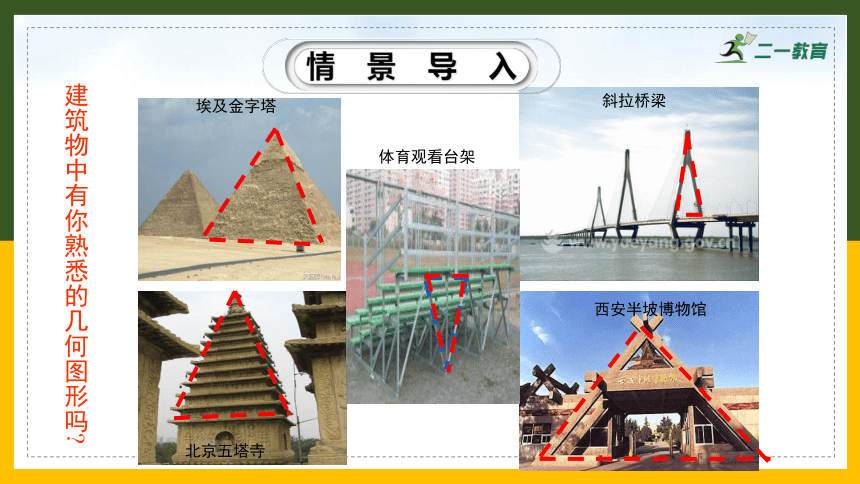
北京五塔寺
西安半坡博物馆
斜拉桥梁
体育观看台架
埃及金字塔
建筑物中有你熟悉的几何图形吗
情景导入
核心知识点一:
全等三角形的判定和性质
两角分别相等且其中一组等角的对边相等的两个三角形全等.
在“平行线的证明”这一章中,我们学了8条基本事实定理.运用这些基本事实和已学习的定理,你能证明有关三角形全等的一些结论吗?
比如:
探索新知
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知和求证;
(4)分析证明思路,写出证明过程.
思考:证明命题的步骤是什么?
探索新知
已知:如图,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
证明:∵∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°(三角形内角和等于180°),
∴∠C=180°-(∠A+∠B),∠F=180°-(∠D+∠E).
∵∠A=∠D,∠B=∠E(已知),
∴∠C=∠F(等量代换).
∵BC=EF(已知),
∴△ABC≌△DEF(ASA).
F
E
D
C
B
A
探索新知
全等三角形判定定理:
两角分别相等且其中一组等角的对边相等的两个三角形全等(AAS).
符号语言:
在△ABC与△A′B′C′中
∴ △ABC≌△A′B′C′(AAS).
探索新知
根据全等三角形的定义,我们可以得到
符号语言:
∵△ABC≌△A′B′C′
∴ ∠A=∠A′,∠B=∠B′ ,∠C=∠C′
AB=A′B′, AC=A′C′, BC=B′C′.
全等三角形的性质:全等三角形的对应边相等、对应角相等.
探索新知
核心知识点二:
等腰三角形的性质及其推论
有两条边相等的三角形叫做等腰三角形。
如图所示△ABC中,AB=AC,则△ABC就是等腰三角形。
注意:只有等腰三角形才有底角和底边.
2、另一条边BC叫做底边;
3、两腰所夹的角∠BAC叫做顶角;
4、底边与腰的夹角∠ABC和∠ACB叫做底角.
1、相等的两条边AB和AC叫做腰;
1.定义:
顶角
底角
底角
底边
A
B
C
相关概念
探索新知
思考:(1)还记得我们知道的等腰三角形的性质吗
(2)你能利用已有的公理和定理证明这些结论吗
自己折纸并观察,试写出等腰三角形的性质.
→
→
D
C
B
A
D
C
B
A
D
(C)
B
A
探索新知
A
B
C
D
如右图所示△ABC具有哪些性质?
角: ① ∠B = ∠C
② ∠BAD=∠CDA
③∠ADC= ∠ADB=900
边: ④BD = CD
对称性:
等腰三角形具有对称性
请你选择等腰三角形的一条性质进行证明
探索新知
证明:等腰三角形的两底角相等.
已知: 如图,在△ABC 中,AB= AC.
求证:∠B= ∠C .
A
B
C
分析:我们曾经利用折叠的方法说明了这两个底角相等. 实际上,折痕将等腰三角形分成了两个全等三角形. 这启发我们,可以作一条辅助线,把原三角形分成两个全等的三角形,从而证明这两个底角相等.
探索新知
证明:等腰三角形的两底角相等.
已知: 如图,在△ABC 中,AB= AC.
求证:∠B= ∠C .
A
B
C
证明:取BC的中点D ,连接AD,
∵ AB=AC, BD=CD , AD=AD,
∴ △ABD≌△ACD (SSS).
∴ ∠B= ∠C (全等三角形的对应角相等) .
D
你还有其他证明方法吗?
探索新知
证明:等腰三角形的两底角相等.
已知: 如图,在△ABC 中,AB= AC.
求证:∠B= ∠C .
A
B
C
D
证明:作顶角∠A的平分线,交BC于D ,
∵ AB=AC, ∠ BAD= ∠ CAD , AD=AD,
∴ △ABD≌△ACD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等) .
探索新知
证明:等腰三角形的两底角相等.
已知: 如图,在△ABC 中,AB= AC.
求证:∠B= ∠C .
A
B
C
D
证明:过点A作底边BC上的高,交BC于D ,
在Rt△ABD和Rt△ACD中,
∵ AB=AC, AD=AD,
∴△ABD≌△ACD (HL).
∴ ∠B= ∠C (全等三角形的对应角相等) .
探索新知
定理:等腰三角形的两底角相等.
这一定理可以简述为:等边对等角.
几何语言:
∵AB=AC(已知)
∴ B= C(等边对角)
探索新知
在证明等腰三角形性质的方法中,不论是作顶角的平分线,还是作底边的中线,或者是底边的高线,都能通过两三角形的全等得出:所作辅助线既是顶角平分线,又是底边中线、高线.
你能总结出这个性质吗?
探索新知
推论:等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合(三线合一).
符号语言:
∵AB=AC,
∴
AD⊥BC.
BD=CD.
∠BAD=∠CAD.
·
D
探索新知
当堂检测
1.等腰三角形的顶角是80°,则底角的度数是( )
A.80° B.70° C.60° D.50°
2.如图,已知△ABC是等腰三角形,AB=BC,BD平分∠ABC,若AC=10,则AD的长为
( )
A.2 B.3
C.4 D.5
D
D
当堂检测
3. 若实数m,n满足等式|m-2|+ =0,且m,n恰好是等腰三角形ABC的两条边的长,则△ABC的周长为 .
4. 等腰三角形的一个内角为50°,则它的顶角的度数为 .
5. (生活情境题)如图所示的“三等分角仪”能三等分任意一个角,它是
由两根有槽的木棒PA,PB组成,两根木棒在点P相连,并可绕点P转动,点C固定,点O,A可在槽内滑动,OA=OC=PC,若∠AOB=45°,则∠P的度数为 .
10
50°或80°
11.25°
当堂检测
6.已知在△ABC中,AB=AC.
(1)如图1,若∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC
= ;
(2)如图2,若∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC
= ;
15°
20°
图1 图2
当堂检测
7.如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF. 求证:AC∥DF.
证明:∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
∴∠F=∠ACB.
∴AC∥DF.
当堂检测
8.如图,点B,F,C,E在同一条直线上,∠AOF=2∠ACB,∠A=∠D,AB=DE. 求证:BF=CE.
证明:∵∠AOF=2∠ACB,∠AOF=∠ACB+∠DFE,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
∴BC=EF.
∴BC-FC=EF-FC,即BF=CE.
证明:∵∠AOF=2∠ACB,∠AOF=∠ACB+∠DFE,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
∴BC=EF.
∴BC-FC=EF-FC,即BF=CE.
当堂检测
9.如图,在△ABC中,D,E是边BC上的两点,连接AD,AE,已知BE=CD,AD=AE. 求证:AB=AC.
证明:∵BE=CD,
∴BD+DE=CE+DE.
∴BD=CE.
∵AD=AE,
∴∠ADE=∠AED.
∴∠ADB=∠AEC.
在△ADB和△AEC中,
∴△ADB≌△AEC(SAS).
∴AB=AC.
1.知识方面:
(1)等腰三角形的性质:等边对等角.
(2)等腰三角形性质的推论:三线合一,即等腰三角
形顶角的平分线、底边上的中线及底边上的高线
互相重合.
2.思想方法:转化思想的应用,等腰三角形的性质是
证明角相等、边相等的重要方法.
感谢收看
第一章 三角形的证明
1.1.1 等腰三角形(1)
北师大版 数学 八年级 下册
学习目标
1、经历“探索-发现-猜想-证明”的过程证明等腰三角形的有关性质,并能运用性质定理去解决实际问题;
2、在证明的过程中发现数学证明的要求和步骤,体会证明思想.
北京五塔寺
西安半坡博物馆
斜拉桥梁
体育观看台架
埃及金字塔
建筑物中有你熟悉的几何图形吗
情景导入
核心知识点一:
全等三角形的判定和性质
两角分别相等且其中一组等角的对边相等的两个三角形全等.
在“平行线的证明”这一章中,我们学了8条基本事实定理.运用这些基本事实和已学习的定理,你能证明有关三角形全等的一些结论吗?
比如:
探索新知
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知和求证;
(4)分析证明思路,写出证明过程.
思考:证明命题的步骤是什么?
探索新知
已知:如图,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
证明:∵∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°(三角形内角和等于180°),
∴∠C=180°-(∠A+∠B),∠F=180°-(∠D+∠E).
∵∠A=∠D,∠B=∠E(已知),
∴∠C=∠F(等量代换).
∵BC=EF(已知),
∴△ABC≌△DEF(ASA).
F
E
D
C
B
A
探索新知
全等三角形判定定理:
两角分别相等且其中一组等角的对边相等的两个三角形全等(AAS).
符号语言:
在△ABC与△A′B′C′中
∴ △ABC≌△A′B′C′(AAS).
探索新知
根据全等三角形的定义,我们可以得到
符号语言:
∵△ABC≌△A′B′C′
∴ ∠A=∠A′,∠B=∠B′ ,∠C=∠C′
AB=A′B′, AC=A′C′, BC=B′C′.
全等三角形的性质:全等三角形的对应边相等、对应角相等.
探索新知
核心知识点二:
等腰三角形的性质及其推论
有两条边相等的三角形叫做等腰三角形。
如图所示△ABC中,AB=AC,则△ABC就是等腰三角形。
注意:只有等腰三角形才有底角和底边.
2、另一条边BC叫做底边;
3、两腰所夹的角∠BAC叫做顶角;
4、底边与腰的夹角∠ABC和∠ACB叫做底角.
1、相等的两条边AB和AC叫做腰;
1.定义:
顶角
底角
底角
底边
A
B
C
相关概念
探索新知
思考:(1)还记得我们知道的等腰三角形的性质吗
(2)你能利用已有的公理和定理证明这些结论吗
自己折纸并观察,试写出等腰三角形的性质.
→
→
D
C
B
A
D
C
B
A
D
(C)
B
A
探索新知
A
B
C
D
如右图所示△ABC具有哪些性质?
角: ① ∠B = ∠C
② ∠BAD=∠CDA
③∠ADC= ∠ADB=900
边: ④BD = CD
对称性:
等腰三角形具有对称性
请你选择等腰三角形的一条性质进行证明
探索新知
证明:等腰三角形的两底角相等.
已知: 如图,在△ABC 中,AB= AC.
求证:∠B= ∠C .
A
B
C
分析:我们曾经利用折叠的方法说明了这两个底角相等. 实际上,折痕将等腰三角形分成了两个全等三角形. 这启发我们,可以作一条辅助线,把原三角形分成两个全等的三角形,从而证明这两个底角相等.
探索新知
证明:等腰三角形的两底角相等.
已知: 如图,在△ABC 中,AB= AC.
求证:∠B= ∠C .
A
B
C
证明:取BC的中点D ,连接AD,
∵ AB=AC, BD=CD , AD=AD,
∴ △ABD≌△ACD (SSS).
∴ ∠B= ∠C (全等三角形的对应角相等) .
D
你还有其他证明方法吗?
探索新知
证明:等腰三角形的两底角相等.
已知: 如图,在△ABC 中,AB= AC.
求证:∠B= ∠C .
A
B
C
D
证明:作顶角∠A的平分线,交BC于D ,
∵ AB=AC, ∠ BAD= ∠ CAD , AD=AD,
∴ △ABD≌△ACD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等) .
探索新知
证明:等腰三角形的两底角相等.
已知: 如图,在△ABC 中,AB= AC.
求证:∠B= ∠C .
A
B
C
D
证明:过点A作底边BC上的高,交BC于D ,
在Rt△ABD和Rt△ACD中,
∵ AB=AC, AD=AD,
∴△ABD≌△ACD (HL).
∴ ∠B= ∠C (全等三角形的对应角相等) .
探索新知
定理:等腰三角形的两底角相等.
这一定理可以简述为:等边对等角.
几何语言:
∵AB=AC(已知)
∴ B= C(等边对角)
探索新知
在证明等腰三角形性质的方法中,不论是作顶角的平分线,还是作底边的中线,或者是底边的高线,都能通过两三角形的全等得出:所作辅助线既是顶角平分线,又是底边中线、高线.
你能总结出这个性质吗?
探索新知
推论:等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合(三线合一).
符号语言:
∵AB=AC,
∴
AD⊥BC.
BD=CD.
∠BAD=∠CAD.
·
D
探索新知
当堂检测
1.等腰三角形的顶角是80°,则底角的度数是( )
A.80° B.70° C.60° D.50°
2.如图,已知△ABC是等腰三角形,AB=BC,BD平分∠ABC,若AC=10,则AD的长为
( )
A.2 B.3
C.4 D.5
D
D
当堂检测
3. 若实数m,n满足等式|m-2|+ =0,且m,n恰好是等腰三角形ABC的两条边的长,则△ABC的周长为 .
4. 等腰三角形的一个内角为50°,则它的顶角的度数为 .
5. (生活情境题)如图所示的“三等分角仪”能三等分任意一个角,它是
由两根有槽的木棒PA,PB组成,两根木棒在点P相连,并可绕点P转动,点C固定,点O,A可在槽内滑动,OA=OC=PC,若∠AOB=45°,则∠P的度数为 .
10
50°或80°
11.25°
当堂检测
6.已知在△ABC中,AB=AC.
(1)如图1,若∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC
= ;
(2)如图2,若∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC
= ;
15°
20°
图1 图2
当堂检测
7.如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF. 求证:AC∥DF.
证明:∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
∴∠F=∠ACB.
∴AC∥DF.
当堂检测
8.如图,点B,F,C,E在同一条直线上,∠AOF=2∠ACB,∠A=∠D,AB=DE. 求证:BF=CE.
证明:∵∠AOF=2∠ACB,∠AOF=∠ACB+∠DFE,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
∴BC=EF.
∴BC-FC=EF-FC,即BF=CE.
证明:∵∠AOF=2∠ACB,∠AOF=∠ACB+∠DFE,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
∴BC=EF.
∴BC-FC=EF-FC,即BF=CE.
当堂检测
9.如图,在△ABC中,D,E是边BC上的两点,连接AD,AE,已知BE=CD,AD=AE. 求证:AB=AC.
证明:∵BE=CD,
∴BD+DE=CE+DE.
∴BD=CE.
∵AD=AE,
∴∠ADE=∠AED.
∴∠ADB=∠AEC.
在△ADB和△AEC中,
∴△ADB≌△AEC(SAS).
∴AB=AC.
1.知识方面:
(1)等腰三角形的性质:等边对等角.
(2)等腰三角形性质的推论:三线合一,即等腰三角
形顶角的平分线、底边上的中线及底边上的高线
互相重合.
2.思想方法:转化思想的应用,等腰三角形的性质是
证明角相等、边相等的重要方法.
感谢收看
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
