北师大版八下1.1.2等腰三角形(2) 课件
文档属性
| 名称 | 北师大版八下1.1.2等腰三角形(2) 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-06 17:40:13 | ||
图片预览







文档简介
(共29张PPT)
第一章 三角形的证明
1.1.2等腰三角形(2)
北师大版 数学 八年级 下册
学习目标
1.探索等腰三角形的轴对称性及相关性质;
2.类比等腰三角形的性质,得出等边三角形的相关性质;
3.应用等腰或等边三角形的性质解决相关数学问题。
情景导入
知识点1
等腰三角形的两底角相等. 简称为等边对等角.
知识点2
等腰三角形顶角的平分线、底边上的中线及
底边上的高线互相重合.
通常称为:等腰三角形“三线合一”.
情景导入
在七下我们已经知道了“三边相等的三角形是等边三角形”,生活中有很多等边三角形,如交通图标、台球室的三角架等,它们都是等边三角形.
思考:在上一节课我们证明等腰三角形的两底角相等,那等边三角形的各角之间有什么关系呢?等腰三角形中有哪些相等的线段?
核心知识点一:
等腰三角形的重要线段的性质
上节课我们证明了等腰三角形的“三线合一”,即顶角的平分线、底边上的高、底边上的中线.
试猜想等腰三角形的两底角的角平分线、两腰上的高、两腰上的中线有什么关系呢?
探索新知
画一画:在纸上画一个等腰三角形。
它们在数量上有何关系?你能证明吗?
在等腰三角形中作出两底角的平分线。
探索新知
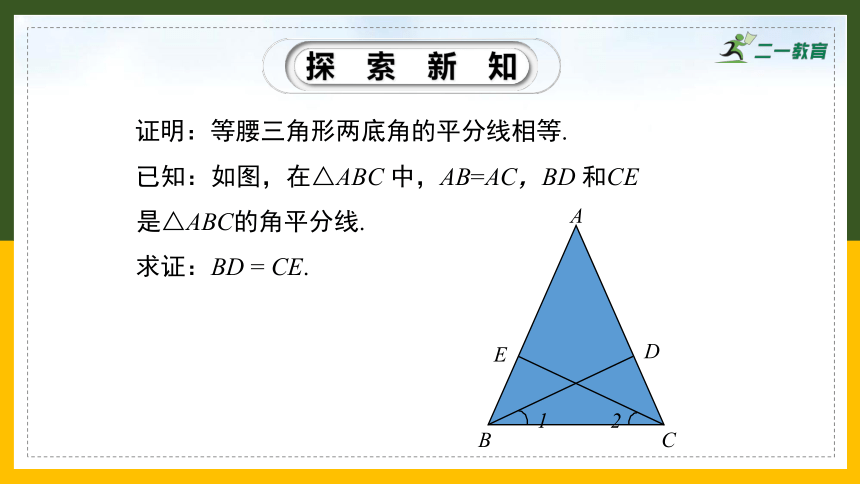
证明:等腰三角形两底角的平分线相等.
已知:如图,在△ABC 中,AB=AC,BD 和CE 是△ABC的角平分线.
求证:BD = CE.
A
B
C
D
E
1
2
探索新知
A
B
C
D
E
1
2
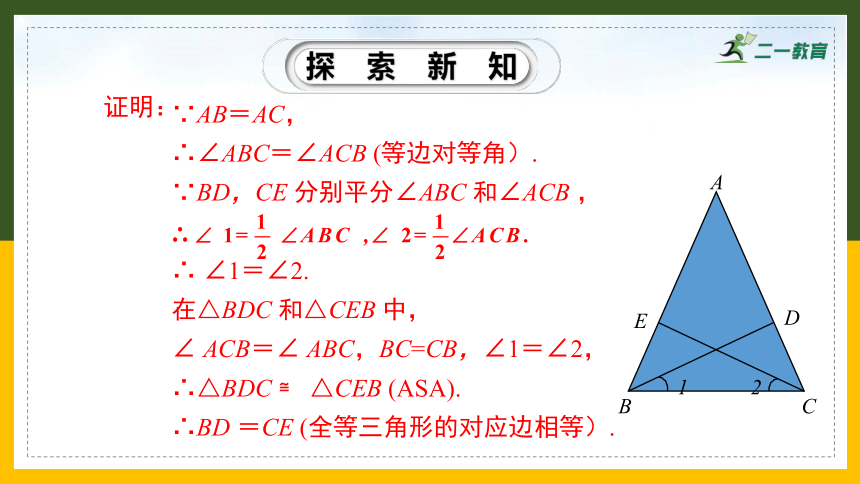
∵AB=AC,
∴∠ABC=∠ACB (等边对等角).
∵BD,CE 分别平分∠ABC 和∠ACB ,
∴ ∠1=∠2.
在△BDC 和△CEB 中,
∠ ACB=∠ ABC,BC=CB,∠1=∠2,
∴△BDC ≌ △CEB (ASA).
∴BD =CE (全等三角形的对应边相等).
证明:
探索新知
归纳总结
等腰三角形两腰上的中线相等吗?高呢?还有其他的结论吗?请你证明它们,并与同伴交流.
等腰三角形两底角的平分线相等.
探索新知
已知:如图,在△ABC 中,AB=AC,BD和CE是△ABC的两腰上的中线. 求证:BD=CE.
A
B
C
D
E
证明: ∵ AB=AC, ∴ ∠ABC= ∠ACB
∵ BD和CE是△ABC两腰上的中线,
∴CD= AC,BE= AB,∴CD= BE.
在△BDC和△CEB 中,
BC=CB,∠ACB=∠ABC,CD= BE ,
∴ △BDC≌△CEB(SAS).
∴ BD=CE(全等三角形的对应边相等).
探索新知
A
C
B
D
E
A
C
B
E
F
A
C
B
P
Q
结论总结:等腰三角形两底角的平分线相等,两腰上的中线相等,两腰上的高相等.
归纳总结
探索新知
已知:如图,在△ABC 中,AB=AC,BD和CE是△ABC的两腰上的高. 求证:BD=CE.
证明: ∵ AB=AC, ∴ ∠ABC= ∠ACB.
∵ BD和CE是△ABC两腰上的高,
∴ ∠BDC= 90°,∠BEC= 90° .
在△BDC 和△CEB 中,
∠ACB= ∠ABC, BC=CB, ∠BDC=∠BEC,
∴ △BDC≌△CEB(AAS).
∴ BD=CE(全等三角形的对应边相等).
A
B
C
D
E
探索新知
归纳总结
如果把等腰三角形两底角的平分线(二等分线)换成三等分线、四等分线,你能得到一个什么结论?
把“等腰三角形两腰上的中线相等”改为“等腰三角形两腰上的三等分线(或四等分线)相等”是否也成立呢?
过底边的端点且与底边夹角相等的两对应线段相等.
两腰上距顶点等距的两点与底边顶点的连线段相等.
探索新知
核心知识点二:
等边三角形的性质
等边三角形是特殊的等腰三角形,那么等边三角形的内角有什么特征呢?
定理 :等边三角形的三个内角都相等,并且每个角都等于60°.
思考: 怎样证明这一定理?
可以利用等腰三角形的性质进行证明.
探索新知
已知:如图, 在△ABC中,AB= AC=BC.
求证:∠A= ∠ B = ∠ C = 60°.
证明:∵AB = AC,
∴∠ B = ∠ C (等边对等角).
又∵AC = BC,
∴∠A= ∠ B (等边对等角).
∴∠A= ∠ B = ∠ C.
在△ABC中,∠A+∠ B+∠ C = 180°.
∴∠A= ∠ B = ∠ C = 60°.
A
B
C
探索新知
(1)等边三角形是轴对称图形吗?如果是,它有几条对称轴?
(2)等边三角形还有哪些特征?
类比拓展:
探索新知
等边三角形的性质:
1.等边三角形是轴对称图形。
2.等边三角形的各角都相等,都等于60°
3.等边三角形每个角的平分线和这个角的对边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。等边三角形共有三条对称轴。
归纳总结
探索新知
当堂检测
1.如图,△ABC是等边三角形,则∠1+∠2= ( )
A.30° B.90° C.120° D.180°
C
当堂检测
2.如图,在等边△ABC中,AF是它的角平分线,若AC=8,则BF=( )
A.4 B.3 C.2 D.1
A
当堂检测
3.如图,在△ABC中,AB=AC,∠BAC=80°,AD是中线,BE是角平分线,AD与BE交于点O,则∠AOB的度数为( )
A.130° B.125°
C.120° D.115°
D
当堂检测
4.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,
DE=5 cm,则BF=( )
A.8 cm B.10 cm
C.12 cm D.14 cm
B
当堂检测
5.如图所示,△ABC是等边三角形,AD∥BC,△ACD是直角三角形,则∠D=________.
30°
当堂检测
5.如图,在等边三角形ABC中,在边BC,AC上取BD=CE,连接AD,BE交于点F.
求证:(1)△ABD≌△BCE;
证明:(1)∵△ABC为等边三角形,
∴AB=AC=BC,∠ABD=∠BCE=60°.
在△ABD和△BCE中,
∴△ABD≌△BCE(SAS).
证明:(1)∵△ABC为等边三角形,
∴AB=AC=BC,∠ABD=∠BCE=60°.
在△ABD和△BCE中,
∴△ABD≌△BCE(SAS).
当堂检测
求证:(2)∠AFE=60°.
证明:(2)由(1),得△ABD≌△BCE,
∴∠BAD=∠CBE.
∵△ABC为等边三角形,
∴∠ABC=60°.
∴∠AFE=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC=60°.
证明:(2)由(1),得△ABD≌△BCE,
∴∠BAD=∠CBE.
∵△ABC为等边三角形,
∴∠ABC=60°.
∴∠AFE=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC=60°.
5.如图,在等边三角形ABC中,在边BC,AC上取BD=CE,连接AD,BE交于点F.
当堂检测
6.如图,△ABC和△ADE都是等边三角形.求证:BD=CE.
证明:∵△ABC和△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
∴△BAD≌△CAE.
∴BD=CE.
证明:∵△ABC和△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
∴△BAD≌△CAE.
∴BD=CE.
当堂检测
7. 如图,△ABC是等边三角形,BD是中线,延长BC到点E,使CE=
CD.
(1)若AB=10,求BE的长;
解:(1)∵△ABC是等边三角形,BD是中线,AB=10,
∴AD=CD= AC= AB=5.
∵CE=CD,
∴CE=5.
∴BE=BC+CE=15.
解:(1)∵△ABC是等边三角形,BD是中线,AB=10,
∴AD=CD= AC= AB=5.
∵CE=CD,
∴CE=5.
∴BE=BC+CE=15.
当堂检测
(2)求∠E的度数.
解:(2)∵△ABC是等边三角形,
∴∠ACB=60°.
∵CE=CD,
∴∠CDE=∠E.
∵∠ACB=∠CDE+∠E,
∴∠E+∠CDE=2∠E=60°.
∴∠E=30°.
解:(2)∵△ABC是等边三角形,
∴∠ACB=60°.
∵CE=CD,
∴∠CDE=∠E.
∵∠ACB=∠CDE+∠E,
∴∠E+∠CDE=2∠E=60°.
∴∠E=30°.
7. 如图,△ABC是等边三角形,BD是中线,延长BC到点E,使CE=
CD.
等边三角形的性质
等边三角形的三个内角都相等,并且每个角都等于60°
等腰三角形重要线段的性质
底角的两条角平分线相等
两条腰上的高相等
两条腰上的中线相等
感谢收看
第一章 三角形的证明
1.1.2等腰三角形(2)
北师大版 数学 八年级 下册
学习目标
1.探索等腰三角形的轴对称性及相关性质;
2.类比等腰三角形的性质,得出等边三角形的相关性质;
3.应用等腰或等边三角形的性质解决相关数学问题。
情景导入
知识点1
等腰三角形的两底角相等. 简称为等边对等角.
知识点2
等腰三角形顶角的平分线、底边上的中线及
底边上的高线互相重合.
通常称为:等腰三角形“三线合一”.
情景导入
在七下我们已经知道了“三边相等的三角形是等边三角形”,生活中有很多等边三角形,如交通图标、台球室的三角架等,它们都是等边三角形.
思考:在上一节课我们证明等腰三角形的两底角相等,那等边三角形的各角之间有什么关系呢?等腰三角形中有哪些相等的线段?
核心知识点一:
等腰三角形的重要线段的性质
上节课我们证明了等腰三角形的“三线合一”,即顶角的平分线、底边上的高、底边上的中线.
试猜想等腰三角形的两底角的角平分线、两腰上的高、两腰上的中线有什么关系呢?
探索新知
画一画:在纸上画一个等腰三角形。
它们在数量上有何关系?你能证明吗?
在等腰三角形中作出两底角的平分线。
探索新知
证明:等腰三角形两底角的平分线相等.
已知:如图,在△ABC 中,AB=AC,BD 和CE 是△ABC的角平分线.
求证:BD = CE.
A
B
C
D
E
1
2
探索新知
A
B
C
D
E
1
2
∵AB=AC,
∴∠ABC=∠ACB (等边对等角).
∵BD,CE 分别平分∠ABC 和∠ACB ,
∴ ∠1=∠2.
在△BDC 和△CEB 中,
∠ ACB=∠ ABC,BC=CB,∠1=∠2,
∴△BDC ≌ △CEB (ASA).
∴BD =CE (全等三角形的对应边相等).
证明:
探索新知
归纳总结
等腰三角形两腰上的中线相等吗?高呢?还有其他的结论吗?请你证明它们,并与同伴交流.
等腰三角形两底角的平分线相等.
探索新知
已知:如图,在△ABC 中,AB=AC,BD和CE是△ABC的两腰上的中线. 求证:BD=CE.
A
B
C
D
E
证明: ∵ AB=AC, ∴ ∠ABC= ∠ACB
∵ BD和CE是△ABC两腰上的中线,
∴CD= AC,BE= AB,∴CD= BE.
在△BDC和△CEB 中,
BC=CB,∠ACB=∠ABC,CD= BE ,
∴ △BDC≌△CEB(SAS).
∴ BD=CE(全等三角形的对应边相等).
探索新知
A
C
B
D
E
A
C
B
E
F
A
C
B
P
Q
结论总结:等腰三角形两底角的平分线相等,两腰上的中线相等,两腰上的高相等.
归纳总结
探索新知
已知:如图,在△ABC 中,AB=AC,BD和CE是△ABC的两腰上的高. 求证:BD=CE.
证明: ∵ AB=AC, ∴ ∠ABC= ∠ACB.
∵ BD和CE是△ABC两腰上的高,
∴ ∠BDC= 90°,∠BEC= 90° .
在△BDC 和△CEB 中,
∠ACB= ∠ABC, BC=CB, ∠BDC=∠BEC,
∴ △BDC≌△CEB(AAS).
∴ BD=CE(全等三角形的对应边相等).
A
B
C
D
E
探索新知
归纳总结
如果把等腰三角形两底角的平分线(二等分线)换成三等分线、四等分线,你能得到一个什么结论?
把“等腰三角形两腰上的中线相等”改为“等腰三角形两腰上的三等分线(或四等分线)相等”是否也成立呢?
过底边的端点且与底边夹角相等的两对应线段相等.
两腰上距顶点等距的两点与底边顶点的连线段相等.
探索新知
核心知识点二:
等边三角形的性质
等边三角形是特殊的等腰三角形,那么等边三角形的内角有什么特征呢?
定理 :等边三角形的三个内角都相等,并且每个角都等于60°.
思考: 怎样证明这一定理?
可以利用等腰三角形的性质进行证明.
探索新知
已知:如图, 在△ABC中,AB= AC=BC.
求证:∠A= ∠ B = ∠ C = 60°.
证明:∵AB = AC,
∴∠ B = ∠ C (等边对等角).
又∵AC = BC,
∴∠A= ∠ B (等边对等角).
∴∠A= ∠ B = ∠ C.
在△ABC中,∠A+∠ B+∠ C = 180°.
∴∠A= ∠ B = ∠ C = 60°.
A
B
C
探索新知
(1)等边三角形是轴对称图形吗?如果是,它有几条对称轴?
(2)等边三角形还有哪些特征?
类比拓展:
探索新知
等边三角形的性质:
1.等边三角形是轴对称图形。
2.等边三角形的各角都相等,都等于60°
3.等边三角形每个角的平分线和这个角的对边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。等边三角形共有三条对称轴。
归纳总结
探索新知
当堂检测
1.如图,△ABC是等边三角形,则∠1+∠2= ( )
A.30° B.90° C.120° D.180°
C
当堂检测
2.如图,在等边△ABC中,AF是它的角平分线,若AC=8,则BF=( )
A.4 B.3 C.2 D.1
A
当堂检测
3.如图,在△ABC中,AB=AC,∠BAC=80°,AD是中线,BE是角平分线,AD与BE交于点O,则∠AOB的度数为( )
A.130° B.125°
C.120° D.115°
D
当堂检测
4.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,
DE=5 cm,则BF=( )
A.8 cm B.10 cm
C.12 cm D.14 cm
B
当堂检测
5.如图所示,△ABC是等边三角形,AD∥BC,△ACD是直角三角形,则∠D=________.
30°
当堂检测
5.如图,在等边三角形ABC中,在边BC,AC上取BD=CE,连接AD,BE交于点F.
求证:(1)△ABD≌△BCE;
证明:(1)∵△ABC为等边三角形,
∴AB=AC=BC,∠ABD=∠BCE=60°.
在△ABD和△BCE中,
∴△ABD≌△BCE(SAS).
证明:(1)∵△ABC为等边三角形,
∴AB=AC=BC,∠ABD=∠BCE=60°.
在△ABD和△BCE中,
∴△ABD≌△BCE(SAS).
当堂检测
求证:(2)∠AFE=60°.
证明:(2)由(1),得△ABD≌△BCE,
∴∠BAD=∠CBE.
∵△ABC为等边三角形,
∴∠ABC=60°.
∴∠AFE=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC=60°.
证明:(2)由(1),得△ABD≌△BCE,
∴∠BAD=∠CBE.
∵△ABC为等边三角形,
∴∠ABC=60°.
∴∠AFE=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC=60°.
5.如图,在等边三角形ABC中,在边BC,AC上取BD=CE,连接AD,BE交于点F.
当堂检测
6.如图,△ABC和△ADE都是等边三角形.求证:BD=CE.
证明:∵△ABC和△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
∴△BAD≌△CAE.
∴BD=CE.
证明:∵△ABC和△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
∴△BAD≌△CAE.
∴BD=CE.
当堂检测
7. 如图,△ABC是等边三角形,BD是中线,延长BC到点E,使CE=
CD.
(1)若AB=10,求BE的长;
解:(1)∵△ABC是等边三角形,BD是中线,AB=10,
∴AD=CD= AC= AB=5.
∵CE=CD,
∴CE=5.
∴BE=BC+CE=15.
解:(1)∵△ABC是等边三角形,BD是中线,AB=10,
∴AD=CD= AC= AB=5.
∵CE=CD,
∴CE=5.
∴BE=BC+CE=15.
当堂检测
(2)求∠E的度数.
解:(2)∵△ABC是等边三角形,
∴∠ACB=60°.
∵CE=CD,
∴∠CDE=∠E.
∵∠ACB=∠CDE+∠E,
∴∠E+∠CDE=2∠E=60°.
∴∠E=30°.
解:(2)∵△ABC是等边三角形,
∴∠ACB=60°.
∵CE=CD,
∴∠CDE=∠E.
∵∠ACB=∠CDE+∠E,
∴∠E+∠CDE=2∠E=60°.
∴∠E=30°.
7. 如图,△ABC是等边三角形,BD是中线,延长BC到点E,使CE=
CD.
等边三角形的性质
等边三角形的三个内角都相等,并且每个角都等于60°
等腰三角形重要线段的性质
底角的两条角平分线相等
两条腰上的高相等
两条腰上的中线相等
感谢收看
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
