北师大九下1.1.1锐角三角函数(1) 课件
文档属性
| 名称 | 北师大九下1.1.1锐角三角函数(1) 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-06 17:55:35 | ||
图片预览





文档简介
(共36张PPT)
第一章直角三角形的边角关系
1.1.1锐角三角函数(1)
北师大版 数学 九年级 下册
学习目标
1.理解锐角的三角函数中正切的概念及其与现实生活的联系;
2.能在直角三角形中求出某个锐角的正切值,并进行简单计算;
3.了解坡度、坡角的概念,能解决与坡度、坡角有关的简单实际问题.
情景导入
对直角三角形的边角关系,已经研究了什么?还可以研究什么?
答:我们前面研究了直角三角形中角与角之间的关系(两锐角互余)、三边之间的关系(勾股定理),还可以研究边与角之间的关系.
情景导入
猜一猜,这座古塔有多高
在直角三角形中,知道一边和一个锐角,你能求出其他的边和角吗
想一想,你能运用所学的数学知识测出这座古塔的高吗
核心知识点一:
正切的定义
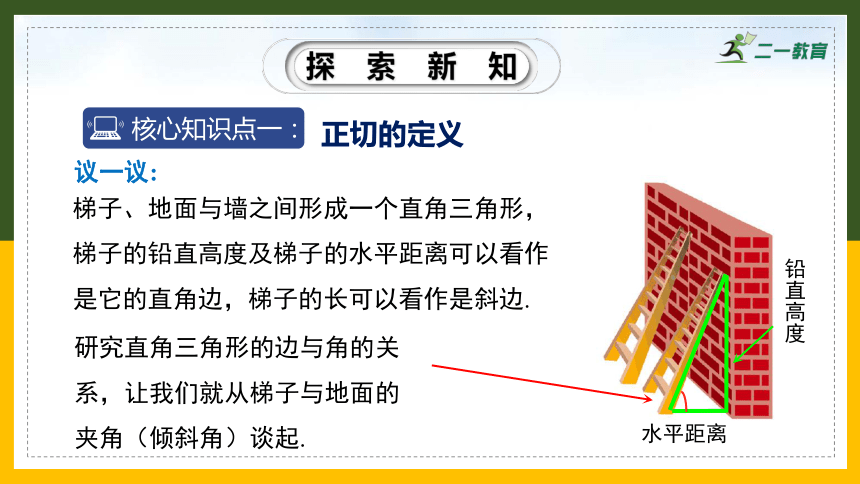
梯子、地面与墙之间形成一个直角三角形,梯子的铅直高度及梯子的水平距离可以看作是它的直角边,梯子的长可以看作是斜边.
铅直高度
水平距离
研究直角三角形的边与角的关系,让我们就从梯子与地面的夹角(倾斜角)谈起.
议一议:
探索新知
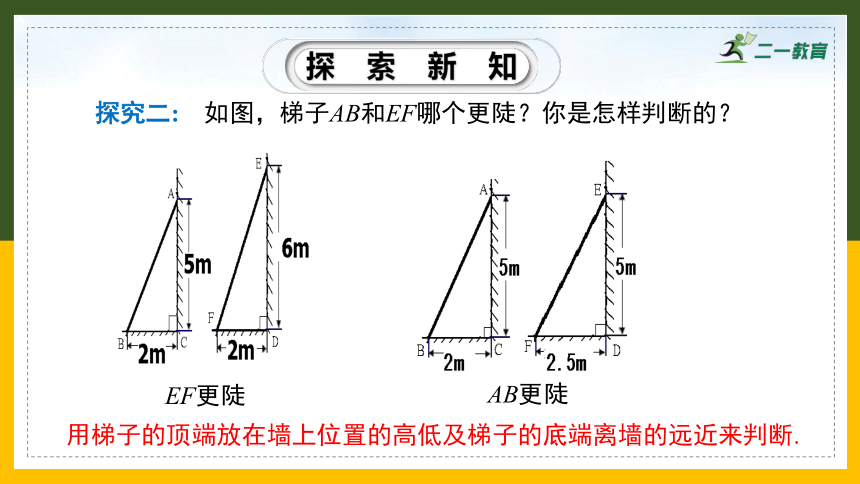
用梯子的顶端放在墙上位置的高低及梯子的底端离墙的远近来判断.
探究二: 如图,梯子AB和EF哪个更陡?你是怎样判断的?
EF更陡
AB更陡
探索新知
3m
3m
2m
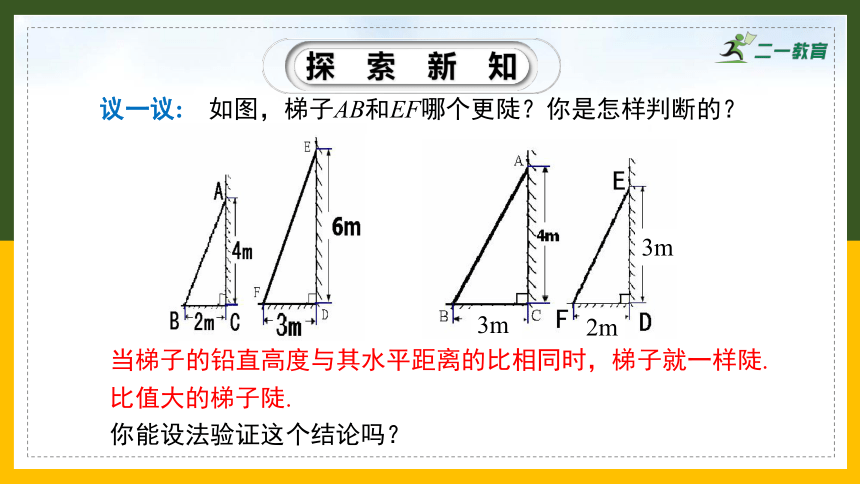
议一议: 如图,梯子AB和EF哪个更陡?你是怎样判断的?
当梯子的铅直高度与其水平距离的比相同时,梯子就一样陡.
比值大的梯子陡.
你能设法验证这个结论吗?
探索新知
A
B1
C1
C2
B2
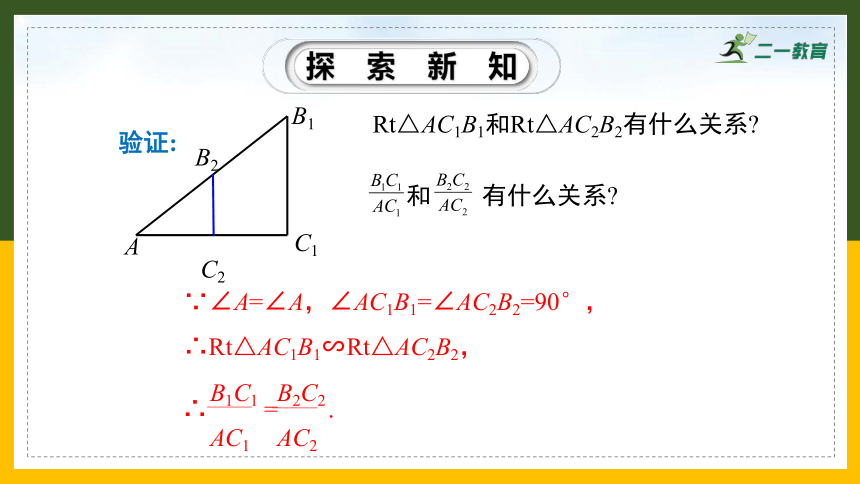
∵∠A=∠A,∠AC1B1=∠AC2B2=90°,
∴Rt△AC1B1∽Rt△AC2B2,
Rt△AC1B1和Rt△AC2B2有什么关系
验证:
和 有什么关系
∴ = .
B1C1
AC1
B2C2
AC2
探索新知
C2
A
B1
C1
B2
B
1.如果任意改变B2在梯子上的位置呢 你有什么想法
∠A的大小确定, ∠A的对边与邻边的比值不变.
2.如果改变∠A 的大小, ∠A的对边与邻边的比值会随之改变吗
∠A的大小改变, ∠A的对边与邻边的比值会随之改变.
探究三:
探索新知
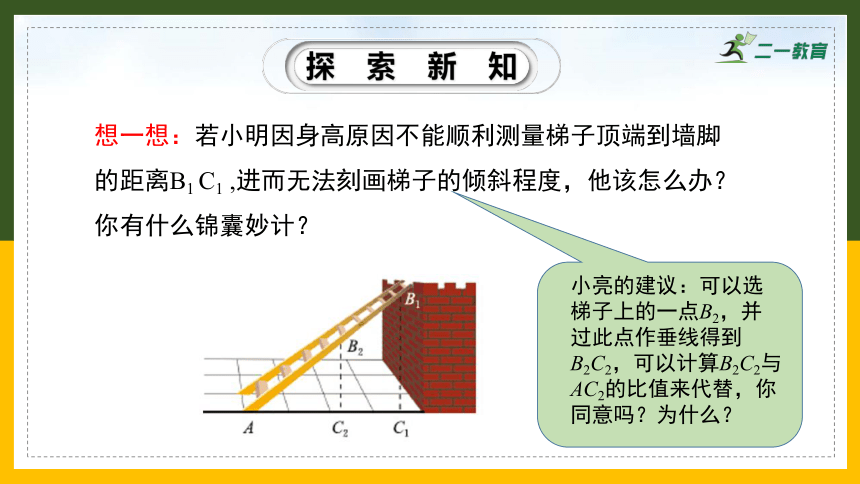
想一想:若小明因身高原因不能顺利测量梯子顶端到墙脚的距离B1 C1 ,进而无法刻画梯子的倾斜程度,他该怎么办?你有什么锦囊妙计?
小亮的建议:可以选梯子上的一点B2,并过此点作垂线得到B2C2,可以计算B2C2与AC2的比值来代替,你同意吗?为什么?
探索新知
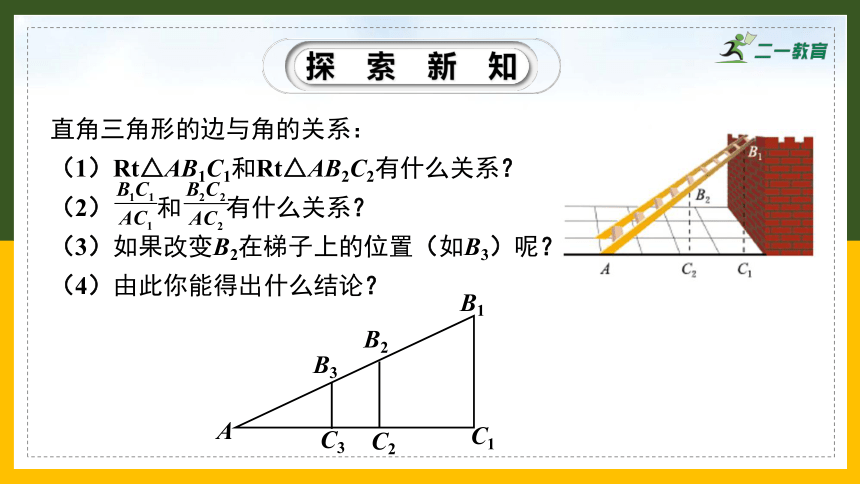
直角三角形的边与角的关系:
(1)Rt△AB1C1和Rt△AB2C2有什么关系?
(2) 和 有什么关系?
(3)如果改变B2在梯子上的位置(如B3)呢?
(4)由此你能得出什么结论?
A
B1
B2
B3
C1
C2
C3
探索新知
A
B1
B2
B3
C1
C2
C3
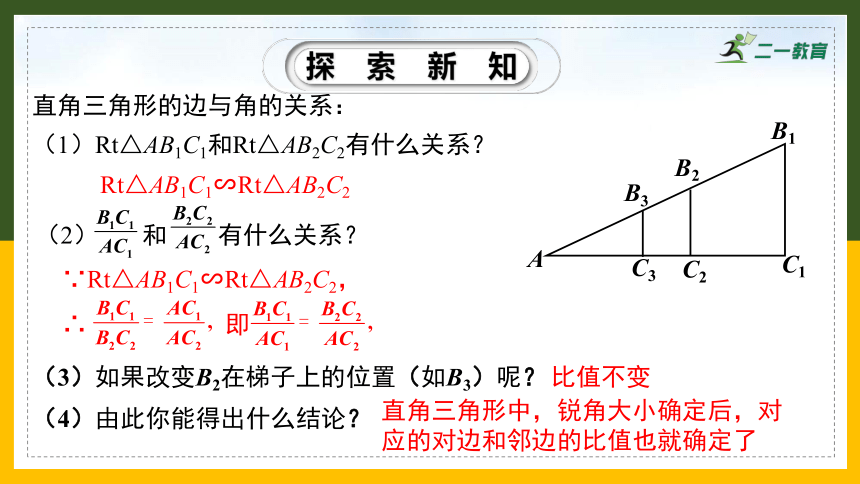
直角三角形的边与角的关系:
(1)Rt△AB1C1和Rt△AB2C2有什么关系?
(2) 和 有什么关系?
Rt△AB1C1∽Rt△AB2C2
(3)如果改变B2在梯子上的位置(如B3)呢?
∵Rt△AB1C1∽Rt△AB2C2,
∴ 即
(4)由此你能得出什么结论?
比值不变
直角三角形中,锐角大小确定后,对应的对边和邻边的比值也就确定了
探索新知
归纳总结
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA,即
A
B
C
∠A的对边
∠A的邻边
┌
tanA=
结论:tanA的值越大,梯子越陡.
探索新知
定义中的几点说明:
1.初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2.tanA是一个完整的符号,它表示∠A的正切.但∠BAC的正切表示为:tan∠BAC.∠1的正切表示为:tan∠1.
3.tanA﹥0 且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序: ).
4.tanA不表示“tan”乘以“A ”.
5.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
探索新知
总结:1.当梯子与地面所成的角为锐角A时,
tan A= tan A的值越大,梯子越陡.
因此可用梯子的倾斜角的正切值来描述梯子的倾斜程度.
2. 当倾斜角确定时,其对边与邻边之比随之确定,这一比
值只与倾斜角的大小有关,而与物体的长度无关.
探索新知
A
B
C
┌
锐角A的正切值可以等于1吗?为什么?可以大于1吗?
对于锐角A的每一个确定的值,tanA都有唯一的确定的值与它对应.
解:可以等于1,此时为等腰直角三角形;也可以大于1,甚至可逼近于无穷大.
议一议
探索新知
总结:直角三角形中求锐角正切值的方法:
(1)若已知两直角边,直接利用正切的定义求解;
(2)若已知一直角边及斜边,另一直角边未知,可先利用勾股定理求出未知的直角边,再利用正切的定义求解.
探索新知
总结:(1)倾斜程度,其本意指倾斜角的大小,一般来说,倾斜角较大的物体,就说它放得更“陡”.
(2)利用物体与地面夹角的正切值来判断物体的倾斜程度,因为夹角的正切值越大,则夹角越大,物体放置得越“陡”.
探索新知
例1: 下图表示两个自动扶梯,哪一个自动扶梯比较陡
解:甲梯中,
β
6m
┐
乙
8m
α
5m
┌
甲
13m
乙梯中,
∵tanβ>tanα,∴乙梯更陡.
提示:在生活中,常用一个锐角的正切表示梯子的倾斜程度.
探索新知
核心知识点二:
坡度、坡角
如图,正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:
100m
60m
┌
α
i
探索新知
1.坡面与水平面的夹角(α)叫坡角。
2.坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切。
3.坡度越大,坡面越陡。
探索新知
例2 如图,一山坡的坡度为i=1:2.小刚从山脚A出发, 沿山坡向上走了240m到达点C.这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到0.1m)?
i=1:2
探索新知
在Rt△ABC中,∠B=90°,∠A=26.57°,AC=240m,
解:
用α表示坡角的大小,由题意可得
因此 α≈26.57°.
答:这座山坡的坡角约为26.57°,小刚上
升了约107.3 m.
从而 BC=240×sin26.57°≈107.3(m).
因此
探索新知
当堂检测
1. 在Rt△ ABC 中,∠ C =90°, AC =4, BC =3,则tan A
等于( A )
A. B. C. D.
A
当堂检测
2. 如图所示,△ ABC 的顶点都在正方形网格的格点上,
则tan C 的值为( A )
A. B. C. D.
A
当堂检测
3. 如图所示,梯子(长度不变)和地面所成的锐角为
∠α,关于∠α的正切值与梯子的倾斜程度的关系,下列
叙述正确的是( C )
A. tanα的值越大,梯子越缓
B. tanα的值越小,梯子越陡
C. tanα的值越大,梯子越陡
D. 梯子的陡缓程度与∠α的正切值无关
C
当堂检测
4. 如图,过∠ MAN 的边 AM 上的一点 B (不与点 A 重
合)作 BC ⊥ AN 于点 C ,过点 C 作 CD ⊥ AM 于点 D ,则
下列线段的比等于tan A 的是( C )
A. B. C. D.
C
当堂检测
5. 如图, A , B , C 三点在正方形网格线的交点处,若
将△ ACB 绕着点 A 逆时针旋转得到△AC'B',则tanB'的值
为( B )
A. B. C. D.
B
当堂检测
6. 如图是某水库大坝的横截面示意图,已知 AD ∥ BC ,且 AD , BC 之间的距离为15米,背水坡 CD 的坡度i =1∶0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端 AE 比原来的顶端 AD 加宽了2米,背水坡 EF 的坡度 i =3∶4,则大坝底端增加的长度 CF 是( C )
A. 7米 B. 11米 C. 13米 D. 20米
C
当堂检测
7. 如图,自贡市在建高铁的某段路基横断面为梯形
ABCD , DC ∥ AB , BC 长6米,坡角β为45°, AD 的坡角
α为30°,则 AD 的长为 米.(结果保留根号)
(第7题图)
6
当堂检测
8. 如图,一段河坝的横截面为四边形 ABCD ,且 BC ∥
AD ,试根据图中数据,求出坝底宽 AD . ( i = CE ∶
ED ,单位:m)
当堂检测
解:作 BF ⊥ AD 于点 F ,易证四边形 BFEC 是矩形,则 BF = CE =4m, EF = BC =4.5m,在Rt△ ABF 中,
AF = = =3m.
在Rt△ CED 中, i = = ,
∴ DE = CE =4 m.
则 AD = AF + EF + DE =3+4.5+4 =(7.5+4 )m.
答:坝底宽 AD 为(7.5+4 )m.
当堂检测
9. 如图,某宾馆在重新装修时,准备在大厅的主楼梯上铺设某种红地毯.如果主楼梯的坡度为1∶ ,且楼梯的铅直高度(即 BC 的长)为3m.
(1)至少需要多长的地毯?(结果保留一位小数)
解:(1)∵主楼梯的坡度为1∶ ,
∴ = .又∵ BC =3m,∴ AB =3 m.
∴地毯长为3 +3≈8.2(m).
答:至少需要8.2m长的地毯.
当堂检测
(2)若所铺设的地毯每平方米售价30元,主楼梯的
宽度为2m,你作为经理至少应给采购人员多少钱去购
买地毯?
解:(2)地毯的面积约为8.2×2=16.4
(m2),则购买地毯的金额为16.4×30=
492(元).
答:至少应给采购人员492元钱去购买地毯.
正切
定义
坡度
∠A越大,tanA越大,
梯子越陡
与梯子倾斜程度的关系
感谢收看
第一章直角三角形的边角关系
1.1.1锐角三角函数(1)
北师大版 数学 九年级 下册
学习目标
1.理解锐角的三角函数中正切的概念及其与现实生活的联系;
2.能在直角三角形中求出某个锐角的正切值,并进行简单计算;
3.了解坡度、坡角的概念,能解决与坡度、坡角有关的简单实际问题.
情景导入
对直角三角形的边角关系,已经研究了什么?还可以研究什么?
答:我们前面研究了直角三角形中角与角之间的关系(两锐角互余)、三边之间的关系(勾股定理),还可以研究边与角之间的关系.
情景导入
猜一猜,这座古塔有多高
在直角三角形中,知道一边和一个锐角,你能求出其他的边和角吗
想一想,你能运用所学的数学知识测出这座古塔的高吗
核心知识点一:
正切的定义
梯子、地面与墙之间形成一个直角三角形,梯子的铅直高度及梯子的水平距离可以看作是它的直角边,梯子的长可以看作是斜边.
铅直高度
水平距离
研究直角三角形的边与角的关系,让我们就从梯子与地面的夹角(倾斜角)谈起.
议一议:
探索新知
用梯子的顶端放在墙上位置的高低及梯子的底端离墙的远近来判断.
探究二: 如图,梯子AB和EF哪个更陡?你是怎样判断的?
EF更陡
AB更陡
探索新知
3m
3m
2m
议一议: 如图,梯子AB和EF哪个更陡?你是怎样判断的?
当梯子的铅直高度与其水平距离的比相同时,梯子就一样陡.
比值大的梯子陡.
你能设法验证这个结论吗?
探索新知
A
B1
C1
C2
B2
∵∠A=∠A,∠AC1B1=∠AC2B2=90°,
∴Rt△AC1B1∽Rt△AC2B2,
Rt△AC1B1和Rt△AC2B2有什么关系
验证:
和 有什么关系
∴ = .
B1C1
AC1
B2C2
AC2
探索新知
C2
A
B1
C1
B2
B
1.如果任意改变B2在梯子上的位置呢 你有什么想法
∠A的大小确定, ∠A的对边与邻边的比值不变.
2.如果改变∠A 的大小, ∠A的对边与邻边的比值会随之改变吗
∠A的大小改变, ∠A的对边与邻边的比值会随之改变.
探究三:
探索新知
想一想:若小明因身高原因不能顺利测量梯子顶端到墙脚的距离B1 C1 ,进而无法刻画梯子的倾斜程度,他该怎么办?你有什么锦囊妙计?
小亮的建议:可以选梯子上的一点B2,并过此点作垂线得到B2C2,可以计算B2C2与AC2的比值来代替,你同意吗?为什么?
探索新知
直角三角形的边与角的关系:
(1)Rt△AB1C1和Rt△AB2C2有什么关系?
(2) 和 有什么关系?
(3)如果改变B2在梯子上的位置(如B3)呢?
(4)由此你能得出什么结论?
A
B1
B2
B3
C1
C2
C3
探索新知
A
B1
B2
B3
C1
C2
C3
直角三角形的边与角的关系:
(1)Rt△AB1C1和Rt△AB2C2有什么关系?
(2) 和 有什么关系?
Rt△AB1C1∽Rt△AB2C2
(3)如果改变B2在梯子上的位置(如B3)呢?
∵Rt△AB1C1∽Rt△AB2C2,
∴ 即
(4)由此你能得出什么结论?
比值不变
直角三角形中,锐角大小确定后,对应的对边和邻边的比值也就确定了
探索新知
归纳总结
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA,即
A
B
C
∠A的对边
∠A的邻边
┌
tanA=
结论:tanA的值越大,梯子越陡.
探索新知
定义中的几点说明:
1.初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2.tanA是一个完整的符号,它表示∠A的正切.但∠BAC的正切表示为:tan∠BAC.∠1的正切表示为:tan∠1.
3.tanA﹥0 且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序: ).
4.tanA不表示“tan”乘以“A ”.
5.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
探索新知
总结:1.当梯子与地面所成的角为锐角A时,
tan A= tan A的值越大,梯子越陡.
因此可用梯子的倾斜角的正切值来描述梯子的倾斜程度.
2. 当倾斜角确定时,其对边与邻边之比随之确定,这一比
值只与倾斜角的大小有关,而与物体的长度无关.
探索新知
A
B
C
┌
锐角A的正切值可以等于1吗?为什么?可以大于1吗?
对于锐角A的每一个确定的值,tanA都有唯一的确定的值与它对应.
解:可以等于1,此时为等腰直角三角形;也可以大于1,甚至可逼近于无穷大.
议一议
探索新知
总结:直角三角形中求锐角正切值的方法:
(1)若已知两直角边,直接利用正切的定义求解;
(2)若已知一直角边及斜边,另一直角边未知,可先利用勾股定理求出未知的直角边,再利用正切的定义求解.
探索新知
总结:(1)倾斜程度,其本意指倾斜角的大小,一般来说,倾斜角较大的物体,就说它放得更“陡”.
(2)利用物体与地面夹角的正切值来判断物体的倾斜程度,因为夹角的正切值越大,则夹角越大,物体放置得越“陡”.
探索新知
例1: 下图表示两个自动扶梯,哪一个自动扶梯比较陡
解:甲梯中,
β
6m
┐
乙
8m
α
5m
┌
甲
13m
乙梯中,
∵tanβ>tanα,∴乙梯更陡.
提示:在生活中,常用一个锐角的正切表示梯子的倾斜程度.
探索新知
核心知识点二:
坡度、坡角
如图,正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:
100m
60m
┌
α
i
探索新知
1.坡面与水平面的夹角(α)叫坡角。
2.坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切。
3.坡度越大,坡面越陡。
探索新知
例2 如图,一山坡的坡度为i=1:2.小刚从山脚A出发, 沿山坡向上走了240m到达点C.这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到0.1m)?
i=1:2
探索新知
在Rt△ABC中,∠B=90°,∠A=26.57°,AC=240m,
解:
用α表示坡角的大小,由题意可得
因此 α≈26.57°.
答:这座山坡的坡角约为26.57°,小刚上
升了约107.3 m.
从而 BC=240×sin26.57°≈107.3(m).
因此
探索新知
当堂检测
1. 在Rt△ ABC 中,∠ C =90°, AC =4, BC =3,则tan A
等于( A )
A. B. C. D.
A
当堂检测
2. 如图所示,△ ABC 的顶点都在正方形网格的格点上,
则tan C 的值为( A )
A. B. C. D.
A
当堂检测
3. 如图所示,梯子(长度不变)和地面所成的锐角为
∠α,关于∠α的正切值与梯子的倾斜程度的关系,下列
叙述正确的是( C )
A. tanα的值越大,梯子越缓
B. tanα的值越小,梯子越陡
C. tanα的值越大,梯子越陡
D. 梯子的陡缓程度与∠α的正切值无关
C
当堂检测
4. 如图,过∠ MAN 的边 AM 上的一点 B (不与点 A 重
合)作 BC ⊥ AN 于点 C ,过点 C 作 CD ⊥ AM 于点 D ,则
下列线段的比等于tan A 的是( C )
A. B. C. D.
C
当堂检测
5. 如图, A , B , C 三点在正方形网格线的交点处,若
将△ ACB 绕着点 A 逆时针旋转得到△AC'B',则tanB'的值
为( B )
A. B. C. D.
B
当堂检测
6. 如图是某水库大坝的横截面示意图,已知 AD ∥ BC ,且 AD , BC 之间的距离为15米,背水坡 CD 的坡度i =1∶0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端 AE 比原来的顶端 AD 加宽了2米,背水坡 EF 的坡度 i =3∶4,则大坝底端增加的长度 CF 是( C )
A. 7米 B. 11米 C. 13米 D. 20米
C
当堂检测
7. 如图,自贡市在建高铁的某段路基横断面为梯形
ABCD , DC ∥ AB , BC 长6米,坡角β为45°, AD 的坡角
α为30°,则 AD 的长为 米.(结果保留根号)
(第7题图)
6
当堂检测
8. 如图,一段河坝的横截面为四边形 ABCD ,且 BC ∥
AD ,试根据图中数据,求出坝底宽 AD . ( i = CE ∶
ED ,单位:m)
当堂检测
解:作 BF ⊥ AD 于点 F ,易证四边形 BFEC 是矩形,则 BF = CE =4m, EF = BC =4.5m,在Rt△ ABF 中,
AF = = =3m.
在Rt△ CED 中, i = = ,
∴ DE = CE =4 m.
则 AD = AF + EF + DE =3+4.5+4 =(7.5+4 )m.
答:坝底宽 AD 为(7.5+4 )m.
当堂检测
9. 如图,某宾馆在重新装修时,准备在大厅的主楼梯上铺设某种红地毯.如果主楼梯的坡度为1∶ ,且楼梯的铅直高度(即 BC 的长)为3m.
(1)至少需要多长的地毯?(结果保留一位小数)
解:(1)∵主楼梯的坡度为1∶ ,
∴ = .又∵ BC =3m,∴ AB =3 m.
∴地毯长为3 +3≈8.2(m).
答:至少需要8.2m长的地毯.
当堂检测
(2)若所铺设的地毯每平方米售价30元,主楼梯的
宽度为2m,你作为经理至少应给采购人员多少钱去购
买地毯?
解:(2)地毯的面积约为8.2×2=16.4
(m2),则购买地毯的金额为16.4×30=
492(元).
答:至少应给采购人员492元钱去购买地毯.
正切
定义
坡度
∠A越大,tanA越大,
梯子越陡
与梯子倾斜程度的关系
感谢收看
