北师大九下1.2 30°,45°,60°角的三角函数值 课件
文档属性
| 名称 | 北师大九下1.2 30°,45°,60°角的三角函数值 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-06 17:58:26 | ||
图片预览







文档简介
(共27张PPT)
第一章直角三角形的边角关系
1.2 30°,45°,60°角的三角函数值
北师大版 数学 九年级 下册
学习目标
1、经历探索30°,45°,60°角的三角函数值的过程,能够进行有关的推理,进一步体会三角函数的意义。
2、能够进行30°,45°,60°角的三角函数值的计算。
3、能够根据30°,45°,60°的三角函数值说明相应的锐角的大小。
情景导入
b
A
B
C
a
┌
c
思考:sinA和cosB,有什么关系
sinA=cosB
如图所示 在 Rt△ABC中,∠C=90°。
tanA·tanB=1
tanA和tanB,有什么关系?
锐角三角函数定义
情景导入
观察一副三角尺,其中有几个锐角?它们分别等于多少度?
(1) sin 30°等于多少?你是怎样得到的?与 同伴进行交流.
(2) cos 30° 等于多少? tan 30° 呢?
核心知识点一:
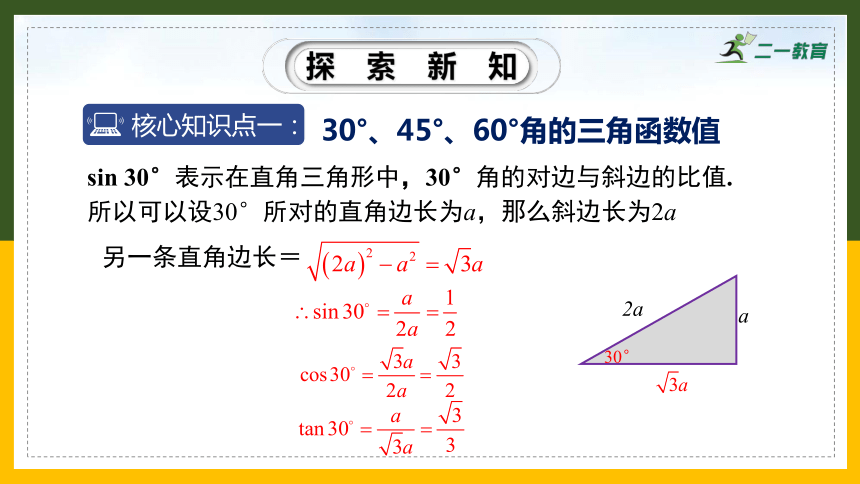
30°、45°、60°角的三角函数值
所以可以设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
sin 30°表示在直角三角形中,30°角的对边与斜边的比值.
30°
a
2a
探索新知
sin 60°表示在直角三角形中,60°角的对边与斜边的比值.
60°
2a
a
探索新知
sin 45°表示在直角三角形中,45°角的对边与斜边的比值.
设直角三角形两条直角边长为a,则斜边长=
45°
a
a
探索新知
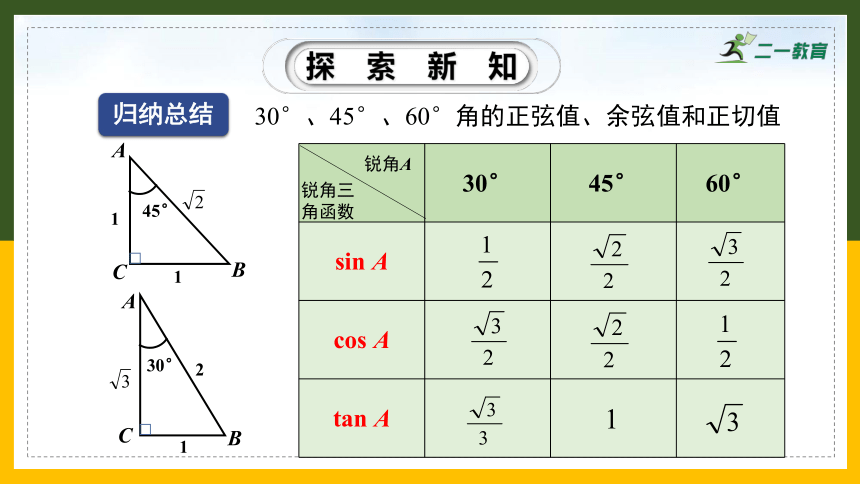
归纳总结
30°、45°、60°角的正弦值、余弦值和正切值
A
B
C
45°
A
B
C
30°
30° 45° 60°
sin A
cos A
tan A
锐角A
锐角三角函数
1
2
1
1
1
探索新知
1.通过特殊角的三角函数值,进一步巩固锐角三角函数之间的关系.(互余关系、倒数关系、相除关系、平方关系)
2.观察特殊三角函数值表,你能得出三角函数的增减性规律吗?
锐角三角函数的增减性:
当角度在0°~90°之间变化时,正弦值和正切值随着角度的增大(或减小)而 ;
余弦值随着角度的增大(或减小)而 .
增大(或减小)
减小(或增大)
两点反思:
探索新知
例1 计算:
(1)sin30°+cos45°; (2) sin260°+cos260°-tan45°.
注意事项:
sin260°表示(sin60°)2,cos260°表示(cos60°)2
解: (1)sin30°+cos45°
(2)sin260°+cos260°-tan45°
探索新知
例2 一个小孩荡秋千,秋千链子的长度为2.5 m,当秋千向两边摆动时,摆角恰好是60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01 m).
探索新知
解:根据题意可知,∠BOD=60°,OB=OA=OD=2.5 m, ∠AOD=30°,
∴OC=ODcos 30 °=
∴AC=2.5-2.165≈0.34(m).
所以,最高位置与最低位置的高度之差约为0.34 m.
探索新知
核心知识点二:
由特殊三角函数值确定锐角度数
填一填
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
逆向思维
探索新知
解: 在图中,
A
B
C
例2 (1) 如图,在Rt△ABC中,∠C = 90°,AB = ,
BC = ,求 ∠A 的度数;
∴ ∠A = 45°.
∵
探索新知
解: 在图中,
A
B
O
∴ α = 60°.
∵ tanα = ,
(2) 如图,AO 是圆锥的高,OB 是底面半径,AO =
OB,求 α 的度数.
探索新知
(1)在Rt△ABC中∠C=90°,当 锐角A>45°时 sinA的值( )
(A)0<sinA< (B) <sinA<1
(C) 0<sinA< (D) <sinA<1
(A)0<cosA< (B) <cosA<1
(C) 0<cosA< (D) <cosA<1
(2) 当锐角A>30°时,cosA的值( )
确定三角函数值的范围
B
C
探索新知
(3)已知 ,下列各式中正确的是( )
(A) < < (B) < <
(C) < < (D) < <
D
(4) 当∠A为锐角,且tanA≤ 1 时,则 ∠A( )
A
(A) 0°<∠A≤45° (B) 45°≤∠A<90°
(C) 0 °<∠A≤30° (D) 30°≤∠A<90
探索新知
当堂检测
1.已知tan =,则锐角α的度数是 ( )
A.60° B.45° C.30° D.75°
2.在△ABC中,∠C=90°,AB=,BC=1,则∠A的度数为 ( )
A.30° B.45° C.60° D.75°
3.在△ABC中,若|sin A-|+(cos B-)2=0,则∠C的度数是________.
A
B
75°
当堂检测
4.小明去爬山,在山脚看山顶角度为30°,小明在坡比为5∶12的山坡上
走1 300米,此时小明看山顶的角度为60°,山高为 ( ) 米.
A.600-250 B.600-250
C.350+350 D.500
B
当堂检测
5.如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑行至B,已知
AB=100米,则这名滑雪运动员的高度下降了________米.
50
当堂检测
6. 计算:
(1)tan 45°-2 sin 60°+ cos 45°;
解:原式=1-2× + ×
=1- +
= - .
当堂检测
(2) cos 30°- +tan 60°;
解:原式= - +
= + -1+ =2 -1.
当堂检测
(3)tan230°+ cos 230°- sin 60°· cos 45°+ sin 45°.
解:原式= + - × + ×
= + - + = - .
当堂检测
7.如图是某市一座人行天桥的示意图,天桥离地面的高BC是10 m,坡面AC的倾斜角∠CAB=45°,在距A点10 m处有一建筑物HQ. 为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3 m宽的人行道,问该建筑物是否需要拆除?(计算最后结果保留一位小数.参考数据: ≈1.414, ≈1.732)
当堂检测
解:由题意,得AH=10 m,BC=10 m,
在Rt△ABC中,∠CAB=45°,∴AB=BC=10 m.
在Rt△DBC中,∠CDB=30°,
∴DB= = =10 (m),
∴DH=AH-AD=AH-(DB-AB)=10-10 +
10=20-10 ≈2.7(m).
∵2.7 m<3 m,∴该建筑物需要拆除.
特殊的锐角三角函数值
30°、45°和60°的三角函数值
sin30°= ,cos30°= ,tan30°=
sin45°= ,cos45°= ,tan45°= 1
sin60°= ,cos60°= ,tan60°= ,
由三角函数值求特殊角
感谢收看
第一章直角三角形的边角关系
1.2 30°,45°,60°角的三角函数值
北师大版 数学 九年级 下册
学习目标
1、经历探索30°,45°,60°角的三角函数值的过程,能够进行有关的推理,进一步体会三角函数的意义。
2、能够进行30°,45°,60°角的三角函数值的计算。
3、能够根据30°,45°,60°的三角函数值说明相应的锐角的大小。
情景导入
b
A
B
C
a
┌
c
思考:sinA和cosB,有什么关系
sinA=cosB
如图所示 在 Rt△ABC中,∠C=90°。
tanA·tanB=1
tanA和tanB,有什么关系?
锐角三角函数定义
情景导入
观察一副三角尺,其中有几个锐角?它们分别等于多少度?
(1) sin 30°等于多少?你是怎样得到的?与 同伴进行交流.
(2) cos 30° 等于多少? tan 30° 呢?
核心知识点一:
30°、45°、60°角的三角函数值
所以可以设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
sin 30°表示在直角三角形中,30°角的对边与斜边的比值.
30°
a
2a
探索新知
sin 60°表示在直角三角形中,60°角的对边与斜边的比值.
60°
2a
a
探索新知
sin 45°表示在直角三角形中,45°角的对边与斜边的比值.
设直角三角形两条直角边长为a,则斜边长=
45°
a
a
探索新知
归纳总结
30°、45°、60°角的正弦值、余弦值和正切值
A
B
C
45°
A
B
C
30°
30° 45° 60°
sin A
cos A
tan A
锐角A
锐角三角函数
1
2
1
1
1
探索新知
1.通过特殊角的三角函数值,进一步巩固锐角三角函数之间的关系.(互余关系、倒数关系、相除关系、平方关系)
2.观察特殊三角函数值表,你能得出三角函数的增减性规律吗?
锐角三角函数的增减性:
当角度在0°~90°之间变化时,正弦值和正切值随着角度的增大(或减小)而 ;
余弦值随着角度的增大(或减小)而 .
增大(或减小)
减小(或增大)
两点反思:
探索新知
例1 计算:
(1)sin30°+cos45°; (2) sin260°+cos260°-tan45°.
注意事项:
sin260°表示(sin60°)2,cos260°表示(cos60°)2
解: (1)sin30°+cos45°
(2)sin260°+cos260°-tan45°
探索新知
例2 一个小孩荡秋千,秋千链子的长度为2.5 m,当秋千向两边摆动时,摆角恰好是60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01 m).
探索新知
解:根据题意可知,∠BOD=60°,OB=OA=OD=2.5 m, ∠AOD=30°,
∴OC=ODcos 30 °=
∴AC=2.5-2.165≈0.34(m).
所以,最高位置与最低位置的高度之差约为0.34 m.
探索新知
核心知识点二:
由特殊三角函数值确定锐角度数
填一填
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
逆向思维
探索新知
解: 在图中,
A
B
C
例2 (1) 如图,在Rt△ABC中,∠C = 90°,AB = ,
BC = ,求 ∠A 的度数;
∴ ∠A = 45°.
∵
探索新知
解: 在图中,
A
B
O
∴ α = 60°.
∵ tanα = ,
(2) 如图,AO 是圆锥的高,OB 是底面半径,AO =
OB,求 α 的度数.
探索新知
(1)在Rt△ABC中∠C=90°,当 锐角A>45°时 sinA的值( )
(A)0<sinA< (B) <sinA<1
(C) 0<sinA< (D) <sinA<1
(A)0<cosA< (B) <cosA<1
(C) 0<cosA< (D) <cosA<1
(2) 当锐角A>30°时,cosA的值( )
确定三角函数值的范围
B
C
探索新知
(3)已知 ,下列各式中正确的是( )
(A) < < (B) < <
(C) < < (D) < <
D
(4) 当∠A为锐角,且tanA≤ 1 时,则 ∠A( )
A
(A) 0°<∠A≤45° (B) 45°≤∠A<90°
(C) 0 °<∠A≤30° (D) 30°≤∠A<90
探索新知
当堂检测
1.已知tan =,则锐角α的度数是 ( )
A.60° B.45° C.30° D.75°
2.在△ABC中,∠C=90°,AB=,BC=1,则∠A的度数为 ( )
A.30° B.45° C.60° D.75°
3.在△ABC中,若|sin A-|+(cos B-)2=0,则∠C的度数是________.
A
B
75°
当堂检测
4.小明去爬山,在山脚看山顶角度为30°,小明在坡比为5∶12的山坡上
走1 300米,此时小明看山顶的角度为60°,山高为 ( ) 米.
A.600-250 B.600-250
C.350+350 D.500
B
当堂检测
5.如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑行至B,已知
AB=100米,则这名滑雪运动员的高度下降了________米.
50
当堂检测
6. 计算:
(1)tan 45°-2 sin 60°+ cos 45°;
解:原式=1-2× + ×
=1- +
= - .
当堂检测
(2) cos 30°- +tan 60°;
解:原式= - +
= + -1+ =2 -1.
当堂检测
(3)tan230°+ cos 230°- sin 60°· cos 45°+ sin 45°.
解:原式= + - × + ×
= + - + = - .
当堂检测
7.如图是某市一座人行天桥的示意图,天桥离地面的高BC是10 m,坡面AC的倾斜角∠CAB=45°,在距A点10 m处有一建筑物HQ. 为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3 m宽的人行道,问该建筑物是否需要拆除?(计算最后结果保留一位小数.参考数据: ≈1.414, ≈1.732)
当堂检测
解:由题意,得AH=10 m,BC=10 m,
在Rt△ABC中,∠CAB=45°,∴AB=BC=10 m.
在Rt△DBC中,∠CDB=30°,
∴DB= = =10 (m),
∴DH=AH-AD=AH-(DB-AB)=10-10 +
10=20-10 ≈2.7(m).
∵2.7 m<3 m,∴该建筑物需要拆除.
特殊的锐角三角函数值
30°、45°和60°的三角函数值
sin30°= ,cos30°= ,tan30°=
sin45°= ,cos45°= ,tan45°= 1
sin60°= ,cos60°= ,tan60°= ,
由三角函数值求特殊角
感谢收看
