北师大九下1.4解直角三角形 课件
图片预览


文档简介
(共29张PPT)
第一章直角三角形的边角关系
1.4解直角三角形
北师大版 数学 九年级 下册
学习目标
1.使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形;
2.渗透数形结合的数学思想,培养学生良好的学习习惯.
情景导入
两锐角的关系:
三边的关系:.
边与角的关系:
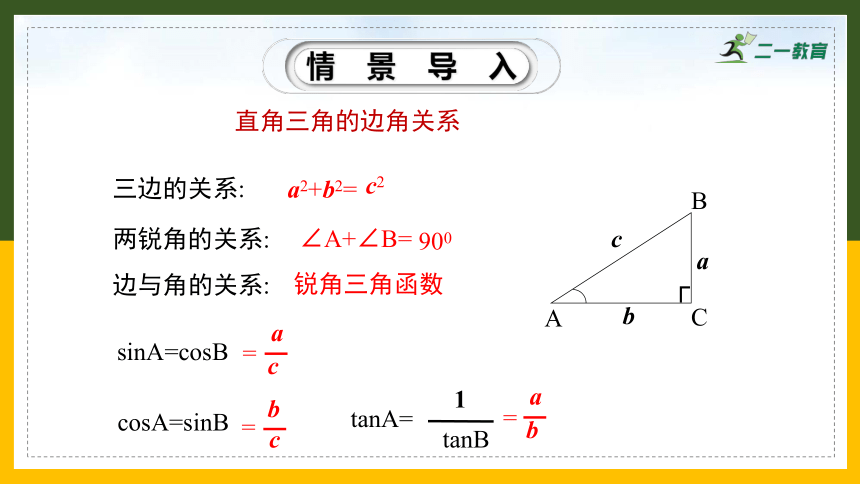
直角三角的边角关系
c2
900
a2+b2=
∠A+∠B=
锐角三角函数
b
A
B
C
a
┌
c
sinA=cosB
cosA=sinB
tanA=
a
c
=
b
c
=
a
b
=
1
tanB
情景导入
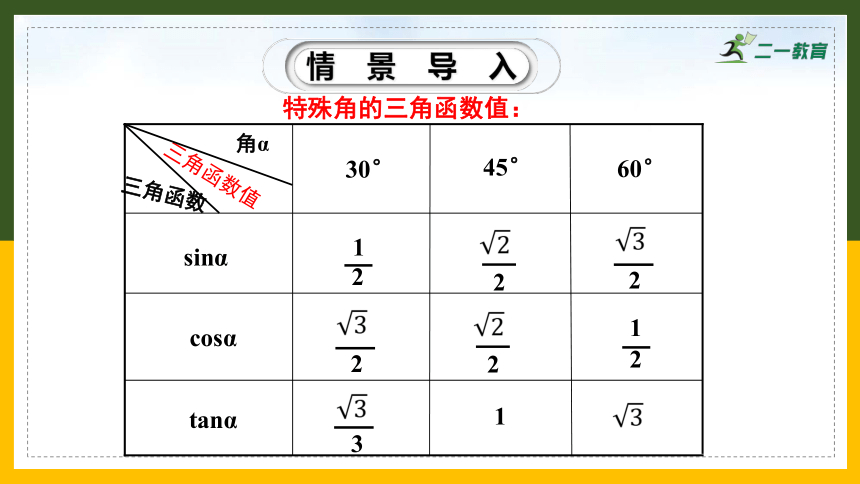
特殊角的三角函数值:
60°
45°
30°
tanα
cosα
sinα
三角函数值
角α
三角函数
1
2
2
3
1
2
2
2
2
1
情景导入
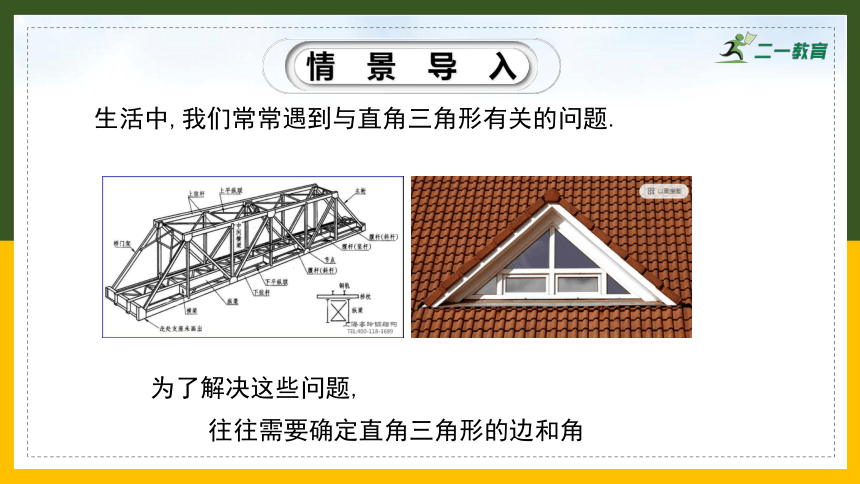
生活中,我们常常遇到与直角三角形有关的问题.
为了解决这些问题,
往往需要确定直角三角形的边和角
核心知识点一:
解直角三角形
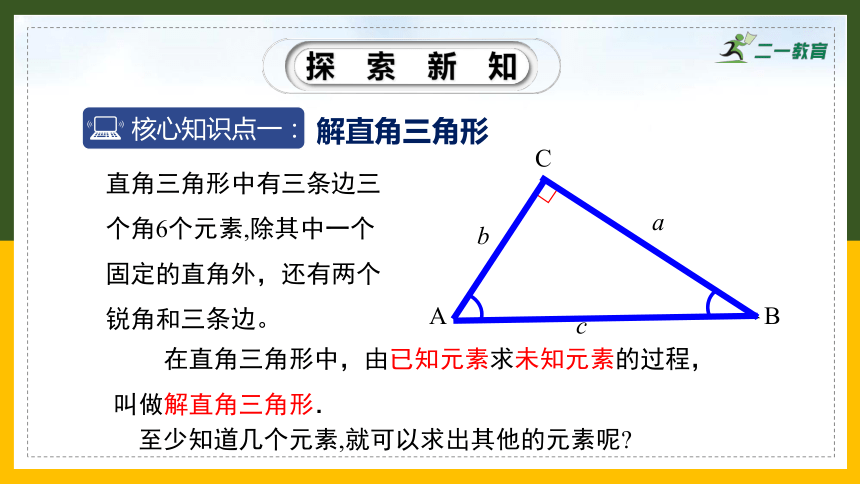
直角三角形中有三条边三个角6个元素,除其中一个固定的直角外,还有两个锐角和三条边。
b
A
B
C
a
c
至少知道几个元素,就可以求出其他的元素呢
∟
在直角三角形中,由已知元素求未知元素的过程,叫做解直角三角形.
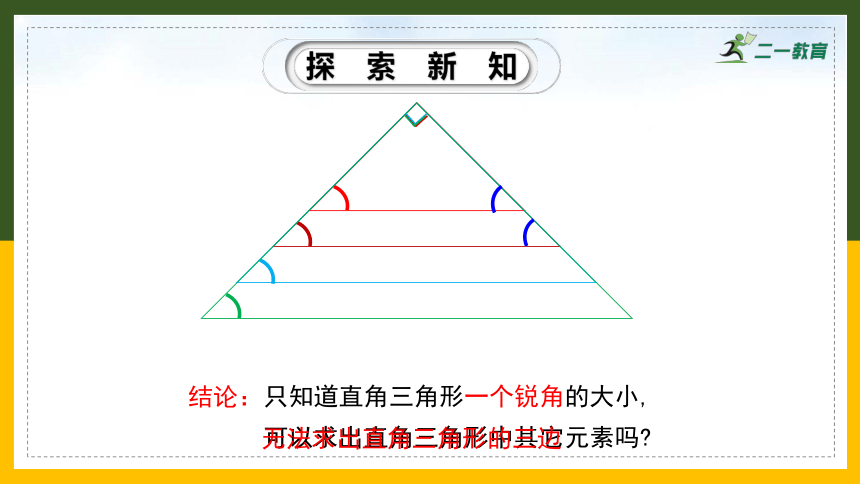
探索新知
只知道直角三角形一个锐角的大小,
可以求出直角三角形中其它元素吗
无法求出直角三角形的三边
结论:
∟
∟
∟
∟
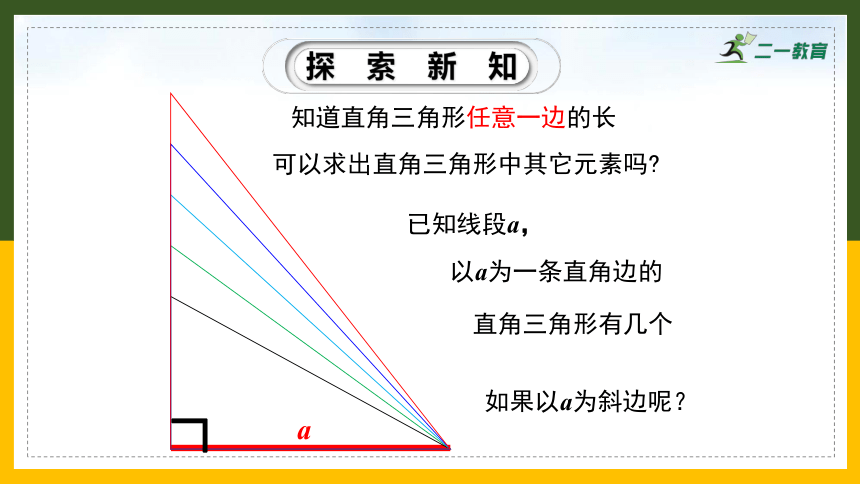
探索新知
∟
知道直角三角形任意一边的长
可以求出直角三角形中其它元素吗
已知线段a,
以a为一条直角边的
直角三角形有几个
如果以a为斜边呢?
a
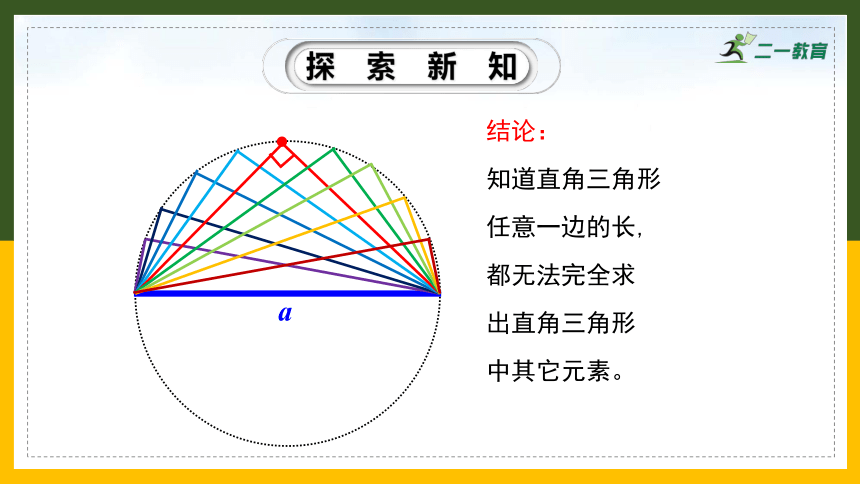
探索新知
都无法完全求
知道直角三角形
任意一边的长,
∟
结论:
出直角三角形
中其它元素。
a
探索新知
在一个直角三角形中,已知一条边和一锐角,或者已知两条边两个元素,才能求出其他元素。
A
B
a
b
c
C
一个直角三角形中,若已知五个元素中的两个元素
(其中必须有一个元素是边),则这样的直角三角形可解.
探索新知
在Rt△ABC中,如果已知其中两边的长,你能求出这个三角形的其他元素吗?
类型1 已知两边解直角三角形
(1)三边之间的关系;
(2)两锐角之间的关系;
(3)边角之间的关系:sin A= =cos B,
cos A= =sin B,
tan A=
探索新知
应用勾股定理求斜边,
应用角的正切值求出
一锐角,再利用直角
三角形的两锐角互余,求出另一锐角.一般不用正弦或余弦值求锐角,因为斜边是一个中间量,如果是近似值,会影响结果的精确度.
已知斜边和直角边:先利用勾股定理求出另一直角边,再求一锐角的正弦和余弦值,即可求出一锐角,再利用直角三角形的两锐角互余,求出另一锐角.
已知两直角边:
已知斜边和直角边:
解直角三角形
探索新知
例1 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且 ,求这个直角三角形的其他元素.
解:在Rt△ABC中,a2+b2=c2,
A
B
C
在Rt△ABC中,
探索新知
例2 已知在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且c=5,b=4,求这个三角形的其他元素.(角度精确到1′)
由c=5,b=4,得sin B= =0.8,
∴∠B≈53°8′.
∴∠A=90°-∠B≈36°52′.
由勾股定理得
解:
探索新知
归纳总结
“已知两边”怎样解直解三角形?
A
B
a
b
c
C
(1)已知a,b,怎么求∠A的度数?
(2)已知a,c,怎么求∠A的度数?
(3)已知b,c,怎么求∠A的度数?
由
由
由
探索新知
已知直角三角形的一边和一锐角,解直角三角形时,若已知一直角边a和一锐角A: ① ∠B=90 °- ∠ A;②c=
若已知斜边c和一个锐角A: ① ∠ B=90°- ∠ A;
②a=c·sin A ; ③b=c·cos A.
类型2 已知一边及一锐角解直角三角形
探索新知
例3 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,∠B=35°,b=20,求这个直角三角形的其他元素(结果保留小数点后一位).
A
B
C
b
20
c
a
35°
解:
探索新知
1、数形结合有利于分析问题;
2、选择关系式时,尽量使用原始数据,以防“累积误差”和“一错再错”;
3、解直角三角形时,应求出所有未知元素。
注意事项:
解直角三角形的原则:
(1)有角先求角,无角先求边
(2)有斜用弦, 无斜用切;
宁乘毋除, 取原避中。
A
B
C
5
50
﹖
探索新知
核心知识点一:
构造直角三角形解决问题
例4 如图,在△ABC中,∠B=30°,∠C=45°,AC=2,求BC.
D
A
B
C
解:过点 A作 AD⊥BC于D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD=sinC·AC=2sin45°= .
在△ABD中,∠B=30°,
∴BD=
∴BC=CD+BD= +
探索新知
C
A
B
D
A
B
C
E
求解非直角三角形的边角问题,常通过添加适当的辅助线,将其转换为直角三角形来解.
提示
D
归纳总结
探索新知
探索新知
1.如图,斜坡AB长20米,其水平宽度AC为10米,则斜坡AB的坡角为( )
A.30° B. 60° C. 1∶ D. 1∶2
A
当堂检测
2.如图,AD是△ABC的高.若BD=2CD=6,tan C=2,则边AB的长为 ( )
A.3 B.3 C.3 D.6
D
当堂检测
3.将一副直角三角板拼成如图1所示的四边形ABCD,一边重合.若∠CAB=45°,∠CAD=30°,连接BD,则tan∠DBC= .
当堂检测
4. 在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,根据已知条件解直角三角形:
(1)a=12,∠A=60°;
解:(1)∵∠A=60°,
∴∠B=90°-∠A=90°-60°=30°,
∴c= =8 ,b= =4 .
当堂检测
4. 在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,根据已知条件解直角三角形:
(2)a=6,b=2 .
解:(2)c= = =4 .
∵tan A= = ,∴∠A=60°,
∴∠B=90°-∠A=30°.
当堂检测
5. 如图,在Rt△ABC中,∠B=90°,点D为BC边上
一点,且满足∠DAB=∠C.
(1)求证:BA2=BD·BC.
(1)证明:∵∠B=∠B,
∠DAB=∠C,
∴△ABD∽△CBA,
∴ = ,
∴BA2=BD·BC.
当堂检测
(2)若AB=3,BC=4,求tan∠DAC的值.
(2)解:如图,过点D作DH⊥AC于点H.
∵BA2=BD·BC,AB=3,BC=4,
∴32=4BD,∴BD= ,
∴CD=BC-BD=4- = .
∵AC= =5,
∴ sin C= = ,即 = ,∴HD= .
即 = ,∴CH= ,
∴AH=AC-CH=5- = ,∴tan∠DAC= = .
解直角三角形
依据
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素
勾股定理
两锐角互余
锐角的三角函数
感谢收看
第一章直角三角形的边角关系
1.4解直角三角形
北师大版 数学 九年级 下册
学习目标
1.使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形;
2.渗透数形结合的数学思想,培养学生良好的学习习惯.
情景导入
两锐角的关系:
三边的关系:.
边与角的关系:
直角三角的边角关系
c2
900
a2+b2=
∠A+∠B=
锐角三角函数
b
A
B
C
a
┌
c
sinA=cosB
cosA=sinB
tanA=
a
c
=
b
c
=
a
b
=
1
tanB
情景导入
特殊角的三角函数值:
60°
45°
30°
tanα
cosα
sinα
三角函数值
角α
三角函数
1
2
2
3
1
2
2
2
2
1
情景导入
生活中,我们常常遇到与直角三角形有关的问题.
为了解决这些问题,
往往需要确定直角三角形的边和角
核心知识点一:
解直角三角形
直角三角形中有三条边三个角6个元素,除其中一个固定的直角外,还有两个锐角和三条边。
b
A
B
C
a
c
至少知道几个元素,就可以求出其他的元素呢
∟
在直角三角形中,由已知元素求未知元素的过程,叫做解直角三角形.
探索新知
只知道直角三角形一个锐角的大小,
可以求出直角三角形中其它元素吗
无法求出直角三角形的三边
结论:
∟
∟
∟
∟
探索新知
∟
知道直角三角形任意一边的长
可以求出直角三角形中其它元素吗
已知线段a,
以a为一条直角边的
直角三角形有几个
如果以a为斜边呢?
a
探索新知
都无法完全求
知道直角三角形
任意一边的长,
∟
结论:
出直角三角形
中其它元素。
a
探索新知
在一个直角三角形中,已知一条边和一锐角,或者已知两条边两个元素,才能求出其他元素。
A
B
a
b
c
C
一个直角三角形中,若已知五个元素中的两个元素
(其中必须有一个元素是边),则这样的直角三角形可解.
探索新知
在Rt△ABC中,如果已知其中两边的长,你能求出这个三角形的其他元素吗?
类型1 已知两边解直角三角形
(1)三边之间的关系;
(2)两锐角之间的关系;
(3)边角之间的关系:sin A= =cos B,
cos A= =sin B,
tan A=
探索新知
应用勾股定理求斜边,
应用角的正切值求出
一锐角,再利用直角
三角形的两锐角互余,求出另一锐角.一般不用正弦或余弦值求锐角,因为斜边是一个中间量,如果是近似值,会影响结果的精确度.
已知斜边和直角边:先利用勾股定理求出另一直角边,再求一锐角的正弦和余弦值,即可求出一锐角,再利用直角三角形的两锐角互余,求出另一锐角.
已知两直角边:
已知斜边和直角边:
解直角三角形
探索新知
例1 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且 ,求这个直角三角形的其他元素.
解:在Rt△ABC中,a2+b2=c2,
A
B
C
在Rt△ABC中,
探索新知
例2 已知在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且c=5,b=4,求这个三角形的其他元素.(角度精确到1′)
由c=5,b=4,得sin B= =0.8,
∴∠B≈53°8′.
∴∠A=90°-∠B≈36°52′.
由勾股定理得
解:
探索新知
归纳总结
“已知两边”怎样解直解三角形?
A
B
a
b
c
C
(1)已知a,b,怎么求∠A的度数?
(2)已知a,c,怎么求∠A的度数?
(3)已知b,c,怎么求∠A的度数?
由
由
由
探索新知
已知直角三角形的一边和一锐角,解直角三角形时,若已知一直角边a和一锐角A: ① ∠B=90 °- ∠ A;②c=
若已知斜边c和一个锐角A: ① ∠ B=90°- ∠ A;
②a=c·sin A ; ③b=c·cos A.
类型2 已知一边及一锐角解直角三角形
探索新知
例3 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,∠B=35°,b=20,求这个直角三角形的其他元素(结果保留小数点后一位).
A
B
C
b
20
c
a
35°
解:
探索新知
1、数形结合有利于分析问题;
2、选择关系式时,尽量使用原始数据,以防“累积误差”和“一错再错”;
3、解直角三角形时,应求出所有未知元素。
注意事项:
解直角三角形的原则:
(1)有角先求角,无角先求边
(2)有斜用弦, 无斜用切;
宁乘毋除, 取原避中。
A
B
C
5
50
﹖
探索新知
核心知识点一:
构造直角三角形解决问题
例4 如图,在△ABC中,∠B=30°,∠C=45°,AC=2,求BC.
D
A
B
C
解:过点 A作 AD⊥BC于D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD=sinC·AC=2sin45°= .
在△ABD中,∠B=30°,
∴BD=
∴BC=CD+BD= +
探索新知
C
A
B
D
A
B
C
E
求解非直角三角形的边角问题,常通过添加适当的辅助线,将其转换为直角三角形来解.
提示
D
归纳总结
探索新知
探索新知
1.如图,斜坡AB长20米,其水平宽度AC为10米,则斜坡AB的坡角为( )
A.30° B. 60° C. 1∶ D. 1∶2
A
当堂检测
2.如图,AD是△ABC的高.若BD=2CD=6,tan C=2,则边AB的长为 ( )
A.3 B.3 C.3 D.6
D
当堂检测
3.将一副直角三角板拼成如图1所示的四边形ABCD,一边重合.若∠CAB=45°,∠CAD=30°,连接BD,则tan∠DBC= .
当堂检测
4. 在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,根据已知条件解直角三角形:
(1)a=12,∠A=60°;
解:(1)∵∠A=60°,
∴∠B=90°-∠A=90°-60°=30°,
∴c= =8 ,b= =4 .
当堂检测
4. 在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,根据已知条件解直角三角形:
(2)a=6,b=2 .
解:(2)c= = =4 .
∵tan A= = ,∴∠A=60°,
∴∠B=90°-∠A=30°.
当堂检测
5. 如图,在Rt△ABC中,∠B=90°,点D为BC边上
一点,且满足∠DAB=∠C.
(1)求证:BA2=BD·BC.
(1)证明:∵∠B=∠B,
∠DAB=∠C,
∴△ABD∽△CBA,
∴ = ,
∴BA2=BD·BC.
当堂检测
(2)若AB=3,BC=4,求tan∠DAC的值.
(2)解:如图,过点D作DH⊥AC于点H.
∵BA2=BD·BC,AB=3,BC=4,
∴32=4BD,∴BD= ,
∴CD=BC-BD=4- = .
∵AC= =5,
∴ sin C= = ,即 = ,∴HD= .
即 = ,∴CH= ,
∴AH=AC-CH=5- = ,∴tan∠DAC= = .
解直角三角形
依据
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素
勾股定理
两锐角互余
锐角的三角函数
感谢收看
