2025年山东德州中考数学模拟试题(含解析)
文档属性
| 名称 | 2025年山东德州中考数学模拟试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-07 07:53:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年山东德州中考数学模拟试题
考试时间:120分钟;总分:150分
学校:___________姓名:___________班级:___________考号:___________
选择题(共12小题,满分48分,每小题4分)
1.在3.14,,,,,中,无理数的个数是( )
A.2 B.3 C.4 D.5
2.2024年6月25日嫦娥六号顺利返回地球,带回大约2kg的月背样本,实现世界首次月背采样返回,标志着我国对月球背面的研究又进入了一个新的高度.已知月球到地球的平均距离约为384000千米,数据384000用科学记数法表示为( )
A.384×103 B.38.4×104 C.3.84×105 D.0.384×106
3.如图,直线AB、CD相交于点O,∠COE为直角,∠AOE=60°,则∠BOD=( )
A.130° B.150° C.120° D.140°
4.如图所示的几何体的左视图是( )
A. B. C. D.
5.下列算式中正确的是( )
A.m3+m2=m5 B.m3 m2=m6 C.m3÷m2=m D.(m3)2=m5
6.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如表所示:
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80
人数 2 3 2 3 4 1
则这15名运动员成绩的众数和中位数分别是( )
A.1.70m和1.60m B.1.70m和1.70m
C.1.75m和1.70m D.1.75m和1.80m
7.《算法统宗》也是我国古代非常重要的数学名著,其中记载了一道题,原文:隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤,几多客人几两银?大意为:有若干客人分银若干两,若每人分7两,则还多4两;若每人分9两,则不足8两.客人有多少?银有多少两?(题中斤、两是旧制质量单位,1斤=16两),设客人有x人,银有y两,根据题意可列方程组为( )
A. B.
C. D.
8.已知x1,x2是一元二次方程x2﹣2x﹣3=0的两个根,则2x1+2x2﹣x1x2的值为( )
A.﹣1 B.1 C.﹣7 D.7
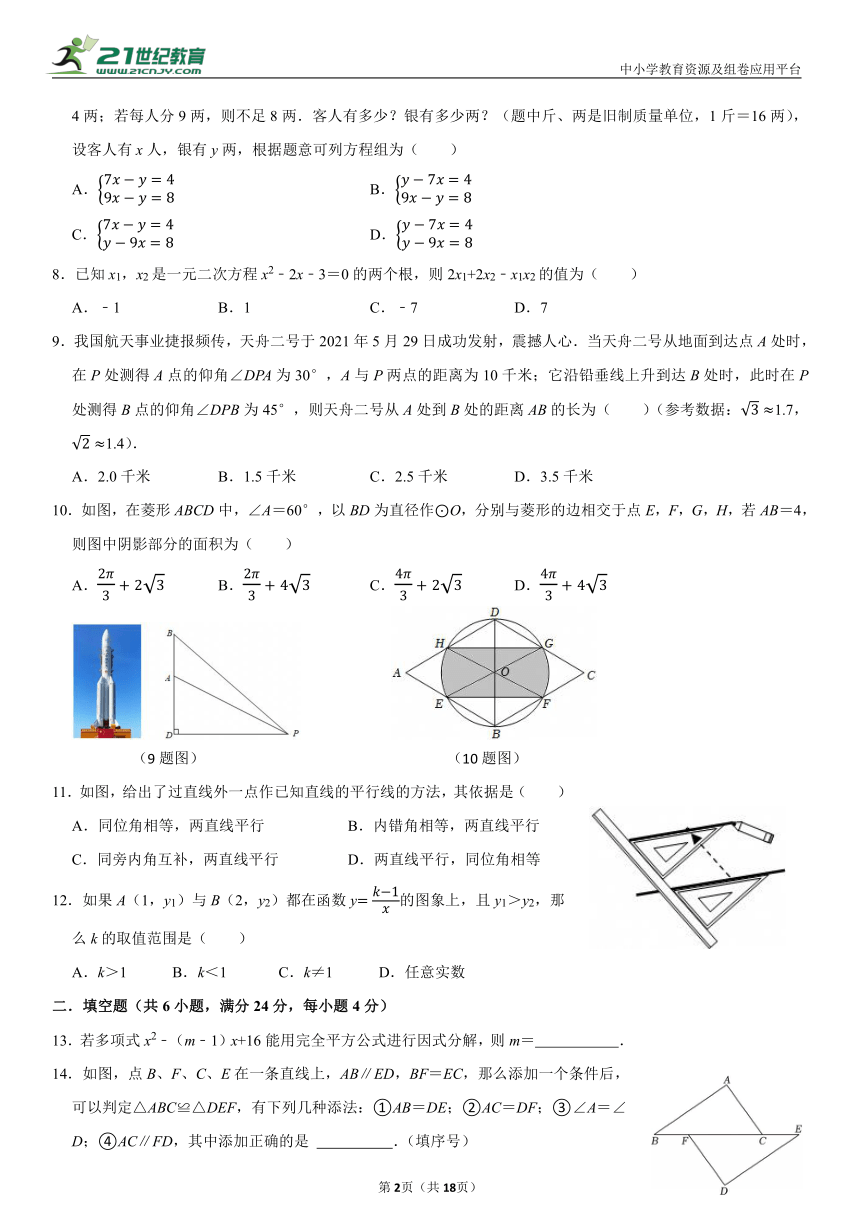
9.我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角∠DPA为30°,A与P两点的距离为10千米;它沿铅垂线上升到达B处时,此时在P处测得B点的仰角∠DPB为45°,则天舟二号从A处到B处的距离AB的长为( )(参考数据:1.7,1.4).
A.2.0千米 B.1.5千米 C.2.5千米 D.3.5千米
10.如图,在菱形ABCD中,∠A=60°,以BD为直径作⊙O,分别与菱形的边相交于点E,F,G,H,若AB=4,则图中阴影部分的面积为( )
A. B. C. D.
(9题图) (10题图)
11.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
12.如果A(1,y1)与B(2,y2)都在函数y的图象上,且y1>y2,那么k的取值范围是( )
A.k>1 B.k<1 C.k≠1 D.任意实数
二.填空题(共6小题,满分24分,每小题4分)
13.若多项式x2﹣(m﹣1)x+16能用完全平方公式进行因式分解,则m= .
14.如图,点B、F、C、E在一条直线上,AB∥ED,BF=EC,那么添加一个条件后,可以判定△ABC≌△DEF,有下列几种添法:①AB=DE;②AC=DF;③∠A=∠D;④AC∥FD,其中添加正确的是 .(填序号)
15.从3、5、6、9四个数中随机取一个数,不放回,再随机取一个数,把第一个数作为十位数字,第二个数作为个位数字,组成一个两位数,则这个两位数是奇数的概率是 .
16.已知a,b是一元二次方程x2﹣4x﹣3=0的两个实数根,则代数式a+b﹣ab的值是 .
17.按一定规律排成的一列数依次为:,,,,,,…,按此规律下去,这列数中的第2020个数是 .
18.有一张如图所示的四边形纸片,AB=AD=6cm,CB=CD=8cm,∠B为直角,要在该纸片中剪出一个面积最大的圆形纸片,则圆形纸片的半径为 cm.
三.解答题(共7小题,满分78分)
19.(8分)(1)化简:; (2)解方程组:.
20.(10分)为深入学习贯彻党的二十大精神,某校开展了以“学习二十大,永远跟党走,奋进新征程”为主题的知识竞赛.发现该校全体学生的竞赛成绩(百分制)均不低于60分,现从中随机抽取n名学生的竞赛成绩进行整理和分析(成绩得分用x表示,共分成四组),并绘制成如下的竞赛成绩分组统计表和扇形统计图,其中“80≤x<90”这组的数据如下:
82,83,83,84,84,85,85,86,86,86,87,89.
竞赛成绩分组统计表
组别 竞赛成绩分组 频数 平均分
1 60≤x<70 8 65
2 70≤x<80 a 76
3 80≤x<90 b 85
4 90≤x≤100 c 94
请根据以上信息,解答下列问题:
(1)c= ;
(2)“80≤x<90”这组数据的众数是 ,方差是 ;
(3)随机抽取的这n名学生竞赛成绩的中位数是 ,平均分是 ;
(4)若学生竞赛成绩达到85分以上(含85分)为优秀,请你估计全校1200名学生中优秀学生的人数.
21.(10分)如图,平行四边形ABCD的两条对角线相交于点O,过点O作OE⊥AB,垂足为E,已知∠DBA=∠DBC,AB=5.
(1)求证:四边形ABCD是菱形;
(2)若,求线段OE的长.
22.(12分)为响应政府发出的创建文明城市的号召,我市计划用两种花卉对某广场进行美化.已知用800元购买A种花卉与用1200元购买B种花卉的数量相等,且B种花卉每盆比A种花卉多1.5元.
(1)求A、B两种花卉每盆各多少元?
(2)计划购买A、B两种花卉共8000盆,其中A种花卉的数量不超过B种花卉数量的,求购买A种花卉多少盆时,购买这批花卉总费用最低,最低费用是多少元?
23.(12分)如图,AB,AC,AD是⊙O中的三条弦,且AD平分∠BAC.
(1)如图1,若∠BAC=120°,测量AB,AC,AD的长度,猜想它们之间的数量关系为: ;
(2)如图2,若∠BAC=90°,求证:;
(3)如图3,若∠BAC=2θ(0°<θ<90°),直接写出AB,AC,AD与θ角三角函数之间的数量关系.
24.(12分)已知二次函数y=x2+bx﹣3(b为常数).
(1)若该函数的图象经过点(3,0),则:
①b的值为 ;
②当﹣3<y<5时,x的取值范围为 .
(2)当m<y<n时(其中m,n为实数,m<n),x的取值范围为﹣1<x<4.直接写出m,n的值或取值范围.
(3)当﹣1≤x≤2时,y的最小值为﹣5,求b的值.
25.(14分)△ABC是等边三角形,点D为线段BC上任意一点,连接AD,E为直线AB上一点.
(1)如图1,当点D为BC中点时,点E在AB边上,连接DE.若AE=1,BE=3,求DE的长;
(2)如图2,若点E为AB延长线上一点,且BE=CD,点F为CB延长线上一点,且∠FAD=60°.猜想线段AF,EF,AD之间存在的数量关系,并证明你的猜想;
(3)如图3,在(1)的条件下,M为线段AD上一点,连接ME,将线段ME绕点E顺时针旋转60°得到线段EN,连接MN.当BN+DN的值最小时,直接写出△AMC的面积.
参考答案
一.选择题(共12小题,满分48分,每小题4分)
1.解:,,是无理数;
选:B.
2.解:384000=3.84×105.
选:C.
3.解:∵∠COE为直角,∠AOE=60°,
∴∠DOE=180°﹣∠COE=180°﹣90°=90°,
∴∠AOD=∠DOE﹣∠AOE=90°﹣60°=30°,
∴∠BOD=180°﹣∠AOD=180°﹣30°=150°.
选:B.
4.解:该几何体的左视图为:
.
选:A.
5.解:A、m3与m2不是同类项,所以不能合并,本选项不合题意;
B、m3 m2=m5,本选项不合题意;
C、m3÷m2=m,本选项符合题意;
D、(m3)2=m6,本选项不合题意;
选:C.
6.解:∵175出现了4次,出现的次数最多,
∴这些运动员成绩的众数是1.75m;
将这15名运动员的成绩从小到大排列,则中位数是1.70m;
选:C.
7.解:由题意可得:,
选:B.
8.解:根据题意得x1+x2=2,x1x2=﹣3,
所以2x1+2x2﹣x1x2=2(x1+x2)﹣x1x2=2×2﹣(﹣3)=7.
选:D.
9.解:在Rt△APD中,∠DPA=30°,AP=10千米,∠ADP=90°,cos∠DPA=cos30°,
∴ADAP10=5(千米),PD=AP cos30°=105(千米),
在Rt△BPD中,tan∠DPB=tan45°,
∴BD=PD tan45°=51=5(千米),
∴AB=BD﹣AD=55≈8.5﹣5=3.5(千米),
选:D.
10.解:连接AC,
∵∠A=60°,AB=4,
∴∠HOE=∠GOF=60°,AB=AD=DC=BC=DB=4,圆半径OD=2,
AO2,AC=4,FG42,△HOG的高为OD2=1,
∴两个扇形面积2×π×22π,两个三角形的面积221=2,
∴阴影部分的面积为π+2.
选:C.
11.解:图中所示过直线外一点作已知直线的平行线,则利用了同位角相等,两直线平行的判定方法.
选:A.
12.解:∵A(1,y1)与B(2,y2)都在函数y的图象上,且y1>y2,
∴k﹣1>0,
∴k>1,
选:A.
二.填空题(共6小题,满分24分,每小题4分)
13.解:∵多项式x2﹣(m﹣1)x+16能用完全平方公式进行因式分解,
∴m﹣1=±8,
解得:m=9或m=﹣7,
答案为:9或﹣7
14.解:∵AB∥ED,
∴∠B=∠E,
∵BF=CE,
∴BC=EF,
∴当AB=DE时,可利用SAS判定△ABC≌△DEF,①符合题意;
当AC=DF时,不能判定△ABC≌△DEF,②不符合题意;
当∠A=∠D时,可利用AAS判定△ABC≌△DEF,③符合题意;
当AC∥FD时,可得∠ACB=∠EFD,利用ASA可判定△ABC≌△DEF,④符合题意;
答案为:①③④.
15.解:画树状图如下:
共有12种等可能的结果,其中组成的两位数是奇数的结果有9种,
∴这个两位数是奇数的概率为,
答案为:.
16.解:∵a,b是一元二次方程x2﹣4x﹣3=0的两个实数根,
∴a+b=4,ab=﹣3
∴a+b﹣ab=4﹣(﹣3)=7,
答案为:7.
17.解:分子可以看出:,,,,,
第2020个数的分子为2,
分母可以看出:第奇数个分母是其个数的平方加1,例如:12+1=2,32+1=10,52+1=26,
第偶数个分母是其个数的平方减1,例如:22﹣1=3,42﹣1=15,62﹣1=35,
这列数中的第2020个数是:.
答案为:.
18.解:连接AC,作∠ABC的角平分线交AC于点E,过点E作EF⊥BC,如图:
∵AB=AD,BC=DC,AC=AC,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,∠ACB=∠ACD,
∴点E到四边形ABCD个边的距离相等,
在该纸片中剪出一个面积最大的圆形纸片,则圆形纸片的圆心为点E,
设半径为r,则BF=r,CF=8﹣r,
AC10cm,
∵∠ABC=90°=∠EFC,
∴△ABC∽△EFC,
∴,即,
解得r,
答案为:.
三.解答题(共7小题,满分78分)
19.解:(1)
=1
=1
;
(2),
①×2﹣②得,﹣4y=﹣8,
解得y=2;
把y=2代入①得,x﹣1=2,
解得x=3,
方程组的解为.
20.解:(1)由题意得,样本容量为:8÷16%=50,
∴c=50×(1﹣16%﹣24%﹣20%)=20.
答案为:20;
(2)80≤x<90”这组的数据的众数是86;
平均分是:(82+83+83+84+84+85+85+86+86+86+87+89)=85,
方差为:[(82﹣85)2+2×(83﹣85)2+2×(84﹣85)2+2×(85﹣85)2+3×(86﹣85)2+(87﹣85)2+(89﹣85)2]=3.5.
答案为:86,3.5;
(3)由题意得,a=50×20%=10,b=50×24%=12,
随机抽取的这n名学生竞赛成绩的中位数是(85+86)÷2=85.5,
平均分是:(65×8+75×10+85×12+95×20)=83.6,
答案为:85.5,83.6;
(4)1200648.
答:估计全校1200名学生中优秀学生的人数约648人.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠DBC,
∵∠DBA=∠DBC,
∴∠ADB=∠DBA,
∴AD=AB,
∴平行四边形ABCD为菱形;
(2)解:∵四边形ABCD为菱形,
∴AC⊥BD,AD=AB=5,OB=OD,
∴∠AOD=90°,
∴sin∠ADB,
∴OAAD=4,
∴OB=OD3,
∵OE⊥AB,
∴△OAB的面积AB OEOA OB,
∴OE.
22.解:(1)设A种花卉每盆a元,B种花卉每盆(a+1.5)元,
,
解得a=3,
经检验,a=3是原分式方程的解,
∴a+1.5=4.5,
答:A种花卉每盆3元,B种花卉每盆4.5元;
(2)设购买A种花卉x盆,则购买B种花卉(8000﹣x)盆,总费用为w元,
由题意可得:w=3x+4.5(8000﹣x)=﹣1.5x+36000,
∴w随x的增大而减小,
∵A种花卉的数量不超过B种花卉数量的,
∴x(8000﹣x),
解得x≤3000,
∴当x=3000时,w取得最小值,此时w=31500,8000﹣x=5000,
答:购买A种花卉3000盆时,购买这批花卉总费用最低,最低费用是31500元.
23.(1)解:AD=AB+AC;
证明:如图1,延长AC至点E,使得CE=AB,连接BD,CD,DE,
∵∠B+∠DCE=180°,∠ACD+∠DCE=180°,
∴∠B=∠DCE,
∵∠BAC=120°,AD平分∠BAC,
∴∠BAD=∠DAC=60°,,
∴BD=CD,
∵AB=CE,
∴△BAD≌△CED(SAS),
∴∠E=∠BAD=60°,
∴∠E=∠BAD=∠ADE=60°,
∴△ADE是等边三角形,
∴AE=AD,
即AD=AB+AC;
答案为:AD=AB+AC;
(2)证明:如图2,延长AC至点E,使得CE=AB,连接BD,CD,DE,
∵∠B+∠DCE=180°,∠ACD+∠DCE=180°,
∴∠B=∠DCE,
∵∠BAC=90°,AD平分∠BAC,
∴∠BAD=∠DAC=45°,,
∴BD=CD,
∵AB=CE,
∴△BAD≌△CED(SAS),
∴∠E=∠BAD=45°,
∴∠E=∠BAD=∠ADE=45°,
∴△ADE是等腰直角三角形,
∴AEAD,
即AB+ACAE;
(3)解:如图3,延长AC至点E,使得CE=AB,连接BD,CD,DE,
∵∠B+∠DCE=180°,∠ACD+∠DCE=180°,
∴∠B=∠DCE,
∵∠BAC=2θ,AD平分∠BAC,
∴∠BAD=∠DAC=θ,,
∴BD=CD,
∵AB=CE,
∴△BAD≌△CED(SAS),
∴∠E=∠BAD=θ,
∴∠E=∠BAD=∠ADE=θ,
∴AD=DE,AE=AB+AC,
过D作DH⊥AE于H,
∴AH=EHAE(AB+AC),
∴cosθ.
24.解:(1)①二次函数y=x2+bx﹣3(b为常数)经过点(3,0),
∴9+3b﹣3=0,
∴b=﹣2,
答案为:﹣2;
②由①知y=x2﹣2x﹣3,
当y>﹣3时,则x2﹣2x﹣3>﹣3,
解得:x<0或x>2,
当y<5时,则x2﹣2x﹣3<5,
解得:﹣2<x<4,
∵a=1>0,
∴当﹣3<y<5时,x的取值范围有两部分,
∴﹣2<x<0或2<x<4,
答案为:﹣2<x<0或2<x<4;
(2)由题意得x的取值只有一段,可知抛物线上横坐标为x=﹣1,x=4的两点关于对称轴对称,
∴,
∴b=﹣3,
∴,
∴时,y有最小值,
∴,
当x=﹣1或x=4时,y=1,
∴n=1;
(3)∵,
∴抛物线的对称轴为,
①当时,y在x=﹣1处取得最小值﹣5,
即(﹣1)2﹣b﹣3=﹣5,
解得b=3;
②当时,y在顶点处取得最小值﹣5,
即,
解得:,
∵2,
∴,
③时,即b≤4,
当x=2,y=﹣5时,b=﹣3(不合题意舍去),
综上所述,b=3或﹣2.
25.解:(1)如图1,
作EF⊥AD于F,
∵△ABC是等边三角形,点D是BC的中点,
∴BC=AB=AE+BE=4,AD⊥BC,BD=CDBC=2,ADAB=2,
∴EF∥BC,
∴△AEF∽△ABD,
∴,
∴AFAD,EF,
∴DF=AD﹣AF,
∴DE;
(2)如图2,
AF=AD+EF,理由如下:
在AF上截取AG=AD,连接BG,
∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠C=∠BAC=60°,
∴∠FAD=∠BAC=60°,
∴∠FAB=∠CAD,
∴△AGB≌△ADC(SAS),
∴∠ABG=∠C=60°,BG=CD,
∴∠FBG=180°﹣∠ABG﹣∠ABC=60°,
∵BE=CD,
∴BG=BE,
∵∠FBE=∠ABC=60°,
∴∠FBE=∠FBG,
∵BF=BF,
∴△FBE≌△FBG(SAS),
∴EF=FG,
∴AF=AG+FG=AD+EF;
(3)如图3,
在AC上截取AW=AE=1,连接WN,
∵∠ABC=60°,
∴△AEW是等边三角形,
∴∠AEW=60°,AE=EW,
∵段ME绕点E顺时针旋转60°得到线段EN,
∴∠MEN=60°,EM=EN,
∴∠MEN=∠AEW,
∴∠AEM=∠WEN,
∴△AEM≌△WEN(SAS),
∴∠EWN=∠BAD=30°,
∴∠AWN=90°,
∴点N在过W且于AW垂直的直线上l运动,
如图4,
作点B关于l的对称点B′,连接DB′交l于点N,直线l交AB于I,B′D交AB于X,
∵∠AGN=90°,AG=1,∠BAC=60°,
∴AI=2AG=2,
∴BI=BD=2,
∵∠ABC=60°,
∴△BDI是等边三角形,
∴XI=BX=1,
∵∠NIX=∠AIG=30°,∠IXN=90°,
∴IN,
∵GI=AG tan60°AG,
∴GN=GI+IN,
∴AM=GN,
∴S△AMCAM CD.
第7页(共17页)
2025年山东德州中考数学模拟试题
考试时间:120分钟;总分:150分
学校:___________姓名:___________班级:___________考号:___________
选择题(共12小题,满分48分,每小题4分)
1.在3.14,,,,,中,无理数的个数是( )
A.2 B.3 C.4 D.5
2.2024年6月25日嫦娥六号顺利返回地球,带回大约2kg的月背样本,实现世界首次月背采样返回,标志着我国对月球背面的研究又进入了一个新的高度.已知月球到地球的平均距离约为384000千米,数据384000用科学记数法表示为( )
A.384×103 B.38.4×104 C.3.84×105 D.0.384×106
3.如图,直线AB、CD相交于点O,∠COE为直角,∠AOE=60°,则∠BOD=( )
A.130° B.150° C.120° D.140°
4.如图所示的几何体的左视图是( )
A. B. C. D.
5.下列算式中正确的是( )
A.m3+m2=m5 B.m3 m2=m6 C.m3÷m2=m D.(m3)2=m5
6.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如表所示:
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80
人数 2 3 2 3 4 1
则这15名运动员成绩的众数和中位数分别是( )
A.1.70m和1.60m B.1.70m和1.70m
C.1.75m和1.70m D.1.75m和1.80m
7.《算法统宗》也是我国古代非常重要的数学名著,其中记载了一道题,原文:隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤,几多客人几两银?大意为:有若干客人分银若干两,若每人分7两,则还多4两;若每人分9两,则不足8两.客人有多少?银有多少两?(题中斤、两是旧制质量单位,1斤=16两),设客人有x人,银有y两,根据题意可列方程组为( )
A. B.
C. D.
8.已知x1,x2是一元二次方程x2﹣2x﹣3=0的两个根,则2x1+2x2﹣x1x2的值为( )
A.﹣1 B.1 C.﹣7 D.7
9.我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角∠DPA为30°,A与P两点的距离为10千米;它沿铅垂线上升到达B处时,此时在P处测得B点的仰角∠DPB为45°,则天舟二号从A处到B处的距离AB的长为( )(参考数据:1.7,1.4).
A.2.0千米 B.1.5千米 C.2.5千米 D.3.5千米
10.如图,在菱形ABCD中,∠A=60°,以BD为直径作⊙O,分别与菱形的边相交于点E,F,G,H,若AB=4,则图中阴影部分的面积为( )
A. B. C. D.
(9题图) (10题图)
11.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
12.如果A(1,y1)与B(2,y2)都在函数y的图象上,且y1>y2,那么k的取值范围是( )
A.k>1 B.k<1 C.k≠1 D.任意实数
二.填空题(共6小题,满分24分,每小题4分)
13.若多项式x2﹣(m﹣1)x+16能用完全平方公式进行因式分解,则m= .
14.如图,点B、F、C、E在一条直线上,AB∥ED,BF=EC,那么添加一个条件后,可以判定△ABC≌△DEF,有下列几种添法:①AB=DE;②AC=DF;③∠A=∠D;④AC∥FD,其中添加正确的是 .(填序号)
15.从3、5、6、9四个数中随机取一个数,不放回,再随机取一个数,把第一个数作为十位数字,第二个数作为个位数字,组成一个两位数,则这个两位数是奇数的概率是 .
16.已知a,b是一元二次方程x2﹣4x﹣3=0的两个实数根,则代数式a+b﹣ab的值是 .
17.按一定规律排成的一列数依次为:,,,,,,…,按此规律下去,这列数中的第2020个数是 .
18.有一张如图所示的四边形纸片,AB=AD=6cm,CB=CD=8cm,∠B为直角,要在该纸片中剪出一个面积最大的圆形纸片,则圆形纸片的半径为 cm.
三.解答题(共7小题,满分78分)
19.(8分)(1)化简:; (2)解方程组:.
20.(10分)为深入学习贯彻党的二十大精神,某校开展了以“学习二十大,永远跟党走,奋进新征程”为主题的知识竞赛.发现该校全体学生的竞赛成绩(百分制)均不低于60分,现从中随机抽取n名学生的竞赛成绩进行整理和分析(成绩得分用x表示,共分成四组),并绘制成如下的竞赛成绩分组统计表和扇形统计图,其中“80≤x<90”这组的数据如下:
82,83,83,84,84,85,85,86,86,86,87,89.
竞赛成绩分组统计表
组别 竞赛成绩分组 频数 平均分
1 60≤x<70 8 65
2 70≤x<80 a 76
3 80≤x<90 b 85
4 90≤x≤100 c 94
请根据以上信息,解答下列问题:
(1)c= ;
(2)“80≤x<90”这组数据的众数是 ,方差是 ;
(3)随机抽取的这n名学生竞赛成绩的中位数是 ,平均分是 ;
(4)若学生竞赛成绩达到85分以上(含85分)为优秀,请你估计全校1200名学生中优秀学生的人数.
21.(10分)如图,平行四边形ABCD的两条对角线相交于点O,过点O作OE⊥AB,垂足为E,已知∠DBA=∠DBC,AB=5.
(1)求证:四边形ABCD是菱形;
(2)若,求线段OE的长.
22.(12分)为响应政府发出的创建文明城市的号召,我市计划用两种花卉对某广场进行美化.已知用800元购买A种花卉与用1200元购买B种花卉的数量相等,且B种花卉每盆比A种花卉多1.5元.
(1)求A、B两种花卉每盆各多少元?
(2)计划购买A、B两种花卉共8000盆,其中A种花卉的数量不超过B种花卉数量的,求购买A种花卉多少盆时,购买这批花卉总费用最低,最低费用是多少元?
23.(12分)如图,AB,AC,AD是⊙O中的三条弦,且AD平分∠BAC.
(1)如图1,若∠BAC=120°,测量AB,AC,AD的长度,猜想它们之间的数量关系为: ;
(2)如图2,若∠BAC=90°,求证:;
(3)如图3,若∠BAC=2θ(0°<θ<90°),直接写出AB,AC,AD与θ角三角函数之间的数量关系.
24.(12分)已知二次函数y=x2+bx﹣3(b为常数).
(1)若该函数的图象经过点(3,0),则:
①b的值为 ;
②当﹣3<y<5时,x的取值范围为 .
(2)当m<y<n时(其中m,n为实数,m<n),x的取值范围为﹣1<x<4.直接写出m,n的值或取值范围.
(3)当﹣1≤x≤2时,y的最小值为﹣5,求b的值.
25.(14分)△ABC是等边三角形,点D为线段BC上任意一点,连接AD,E为直线AB上一点.
(1)如图1,当点D为BC中点时,点E在AB边上,连接DE.若AE=1,BE=3,求DE的长;
(2)如图2,若点E为AB延长线上一点,且BE=CD,点F为CB延长线上一点,且∠FAD=60°.猜想线段AF,EF,AD之间存在的数量关系,并证明你的猜想;
(3)如图3,在(1)的条件下,M为线段AD上一点,连接ME,将线段ME绕点E顺时针旋转60°得到线段EN,连接MN.当BN+DN的值最小时,直接写出△AMC的面积.
参考答案
一.选择题(共12小题,满分48分,每小题4分)
1.解:,,是无理数;
选:B.
2.解:384000=3.84×105.
选:C.
3.解:∵∠COE为直角,∠AOE=60°,
∴∠DOE=180°﹣∠COE=180°﹣90°=90°,
∴∠AOD=∠DOE﹣∠AOE=90°﹣60°=30°,
∴∠BOD=180°﹣∠AOD=180°﹣30°=150°.
选:B.
4.解:该几何体的左视图为:
.
选:A.
5.解:A、m3与m2不是同类项,所以不能合并,本选项不合题意;
B、m3 m2=m5,本选项不合题意;
C、m3÷m2=m,本选项符合题意;
D、(m3)2=m6,本选项不合题意;
选:C.
6.解:∵175出现了4次,出现的次数最多,
∴这些运动员成绩的众数是1.75m;
将这15名运动员的成绩从小到大排列,则中位数是1.70m;
选:C.
7.解:由题意可得:,
选:B.
8.解:根据题意得x1+x2=2,x1x2=﹣3,
所以2x1+2x2﹣x1x2=2(x1+x2)﹣x1x2=2×2﹣(﹣3)=7.
选:D.
9.解:在Rt△APD中,∠DPA=30°,AP=10千米,∠ADP=90°,cos∠DPA=cos30°,
∴ADAP10=5(千米),PD=AP cos30°=105(千米),
在Rt△BPD中,tan∠DPB=tan45°,
∴BD=PD tan45°=51=5(千米),
∴AB=BD﹣AD=55≈8.5﹣5=3.5(千米),
选:D.
10.解:连接AC,
∵∠A=60°,AB=4,
∴∠HOE=∠GOF=60°,AB=AD=DC=BC=DB=4,圆半径OD=2,
AO2,AC=4,FG42,△HOG的高为OD2=1,
∴两个扇形面积2×π×22π,两个三角形的面积221=2,
∴阴影部分的面积为π+2.
选:C.
11.解:图中所示过直线外一点作已知直线的平行线,则利用了同位角相等,两直线平行的判定方法.
选:A.
12.解:∵A(1,y1)与B(2,y2)都在函数y的图象上,且y1>y2,
∴k﹣1>0,
∴k>1,
选:A.
二.填空题(共6小题,满分24分,每小题4分)
13.解:∵多项式x2﹣(m﹣1)x+16能用完全平方公式进行因式分解,
∴m﹣1=±8,
解得:m=9或m=﹣7,
答案为:9或﹣7
14.解:∵AB∥ED,
∴∠B=∠E,
∵BF=CE,
∴BC=EF,
∴当AB=DE时,可利用SAS判定△ABC≌△DEF,①符合题意;
当AC=DF时,不能判定△ABC≌△DEF,②不符合题意;
当∠A=∠D时,可利用AAS判定△ABC≌△DEF,③符合题意;
当AC∥FD时,可得∠ACB=∠EFD,利用ASA可判定△ABC≌△DEF,④符合题意;
答案为:①③④.
15.解:画树状图如下:
共有12种等可能的结果,其中组成的两位数是奇数的结果有9种,
∴这个两位数是奇数的概率为,
答案为:.
16.解:∵a,b是一元二次方程x2﹣4x﹣3=0的两个实数根,
∴a+b=4,ab=﹣3
∴a+b﹣ab=4﹣(﹣3)=7,
答案为:7.
17.解:分子可以看出:,,,,,
第2020个数的分子为2,
分母可以看出:第奇数个分母是其个数的平方加1,例如:12+1=2,32+1=10,52+1=26,
第偶数个分母是其个数的平方减1,例如:22﹣1=3,42﹣1=15,62﹣1=35,
这列数中的第2020个数是:.
答案为:.
18.解:连接AC,作∠ABC的角平分线交AC于点E,过点E作EF⊥BC,如图:
∵AB=AD,BC=DC,AC=AC,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,∠ACB=∠ACD,
∴点E到四边形ABCD个边的距离相等,
在该纸片中剪出一个面积最大的圆形纸片,则圆形纸片的圆心为点E,
设半径为r,则BF=r,CF=8﹣r,
AC10cm,
∵∠ABC=90°=∠EFC,
∴△ABC∽△EFC,
∴,即,
解得r,
答案为:.
三.解答题(共7小题,满分78分)
19.解:(1)
=1
=1
;
(2),
①×2﹣②得,﹣4y=﹣8,
解得y=2;
把y=2代入①得,x﹣1=2,
解得x=3,
方程组的解为.
20.解:(1)由题意得,样本容量为:8÷16%=50,
∴c=50×(1﹣16%﹣24%﹣20%)=20.
答案为:20;
(2)80≤x<90”这组的数据的众数是86;
平均分是:(82+83+83+84+84+85+85+86+86+86+87+89)=85,
方差为:[(82﹣85)2+2×(83﹣85)2+2×(84﹣85)2+2×(85﹣85)2+3×(86﹣85)2+(87﹣85)2+(89﹣85)2]=3.5.
答案为:86,3.5;
(3)由题意得,a=50×20%=10,b=50×24%=12,
随机抽取的这n名学生竞赛成绩的中位数是(85+86)÷2=85.5,
平均分是:(65×8+75×10+85×12+95×20)=83.6,
答案为:85.5,83.6;
(4)1200648.
答:估计全校1200名学生中优秀学生的人数约648人.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠DBC,
∵∠DBA=∠DBC,
∴∠ADB=∠DBA,
∴AD=AB,
∴平行四边形ABCD为菱形;
(2)解:∵四边形ABCD为菱形,
∴AC⊥BD,AD=AB=5,OB=OD,
∴∠AOD=90°,
∴sin∠ADB,
∴OAAD=4,
∴OB=OD3,
∵OE⊥AB,
∴△OAB的面积AB OEOA OB,
∴OE.
22.解:(1)设A种花卉每盆a元,B种花卉每盆(a+1.5)元,
,
解得a=3,
经检验,a=3是原分式方程的解,
∴a+1.5=4.5,
答:A种花卉每盆3元,B种花卉每盆4.5元;
(2)设购买A种花卉x盆,则购买B种花卉(8000﹣x)盆,总费用为w元,
由题意可得:w=3x+4.5(8000﹣x)=﹣1.5x+36000,
∴w随x的增大而减小,
∵A种花卉的数量不超过B种花卉数量的,
∴x(8000﹣x),
解得x≤3000,
∴当x=3000时,w取得最小值,此时w=31500,8000﹣x=5000,
答:购买A种花卉3000盆时,购买这批花卉总费用最低,最低费用是31500元.
23.(1)解:AD=AB+AC;
证明:如图1,延长AC至点E,使得CE=AB,连接BD,CD,DE,
∵∠B+∠DCE=180°,∠ACD+∠DCE=180°,
∴∠B=∠DCE,
∵∠BAC=120°,AD平分∠BAC,
∴∠BAD=∠DAC=60°,,
∴BD=CD,
∵AB=CE,
∴△BAD≌△CED(SAS),
∴∠E=∠BAD=60°,
∴∠E=∠BAD=∠ADE=60°,
∴△ADE是等边三角形,
∴AE=AD,
即AD=AB+AC;
答案为:AD=AB+AC;
(2)证明:如图2,延长AC至点E,使得CE=AB,连接BD,CD,DE,
∵∠B+∠DCE=180°,∠ACD+∠DCE=180°,
∴∠B=∠DCE,
∵∠BAC=90°,AD平分∠BAC,
∴∠BAD=∠DAC=45°,,
∴BD=CD,
∵AB=CE,
∴△BAD≌△CED(SAS),
∴∠E=∠BAD=45°,
∴∠E=∠BAD=∠ADE=45°,
∴△ADE是等腰直角三角形,
∴AEAD,
即AB+ACAE;
(3)解:如图3,延长AC至点E,使得CE=AB,连接BD,CD,DE,
∵∠B+∠DCE=180°,∠ACD+∠DCE=180°,
∴∠B=∠DCE,
∵∠BAC=2θ,AD平分∠BAC,
∴∠BAD=∠DAC=θ,,
∴BD=CD,
∵AB=CE,
∴△BAD≌△CED(SAS),
∴∠E=∠BAD=θ,
∴∠E=∠BAD=∠ADE=θ,
∴AD=DE,AE=AB+AC,
过D作DH⊥AE于H,
∴AH=EHAE(AB+AC),
∴cosθ.
24.解:(1)①二次函数y=x2+bx﹣3(b为常数)经过点(3,0),
∴9+3b﹣3=0,
∴b=﹣2,
答案为:﹣2;
②由①知y=x2﹣2x﹣3,
当y>﹣3时,则x2﹣2x﹣3>﹣3,
解得:x<0或x>2,
当y<5时,则x2﹣2x﹣3<5,
解得:﹣2<x<4,
∵a=1>0,
∴当﹣3<y<5时,x的取值范围有两部分,
∴﹣2<x<0或2<x<4,
答案为:﹣2<x<0或2<x<4;
(2)由题意得x的取值只有一段,可知抛物线上横坐标为x=﹣1,x=4的两点关于对称轴对称,
∴,
∴b=﹣3,
∴,
∴时,y有最小值,
∴,
当x=﹣1或x=4时,y=1,
∴n=1;
(3)∵,
∴抛物线的对称轴为,
①当时,y在x=﹣1处取得最小值﹣5,
即(﹣1)2﹣b﹣3=﹣5,
解得b=3;
②当时,y在顶点处取得最小值﹣5,
即,
解得:,
∵2,
∴,
③时,即b≤4,
当x=2,y=﹣5时,b=﹣3(不合题意舍去),
综上所述,b=3或﹣2.
25.解:(1)如图1,
作EF⊥AD于F,
∵△ABC是等边三角形,点D是BC的中点,
∴BC=AB=AE+BE=4,AD⊥BC,BD=CDBC=2,ADAB=2,
∴EF∥BC,
∴△AEF∽△ABD,
∴,
∴AFAD,EF,
∴DF=AD﹣AF,
∴DE;
(2)如图2,
AF=AD+EF,理由如下:
在AF上截取AG=AD,连接BG,
∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠C=∠BAC=60°,
∴∠FAD=∠BAC=60°,
∴∠FAB=∠CAD,
∴△AGB≌△ADC(SAS),
∴∠ABG=∠C=60°,BG=CD,
∴∠FBG=180°﹣∠ABG﹣∠ABC=60°,
∵BE=CD,
∴BG=BE,
∵∠FBE=∠ABC=60°,
∴∠FBE=∠FBG,
∵BF=BF,
∴△FBE≌△FBG(SAS),
∴EF=FG,
∴AF=AG+FG=AD+EF;
(3)如图3,
在AC上截取AW=AE=1,连接WN,
∵∠ABC=60°,
∴△AEW是等边三角形,
∴∠AEW=60°,AE=EW,
∵段ME绕点E顺时针旋转60°得到线段EN,
∴∠MEN=60°,EM=EN,
∴∠MEN=∠AEW,
∴∠AEM=∠WEN,
∴△AEM≌△WEN(SAS),
∴∠EWN=∠BAD=30°,
∴∠AWN=90°,
∴点N在过W且于AW垂直的直线上l运动,
如图4,
作点B关于l的对称点B′,连接DB′交l于点N,直线l交AB于I,B′D交AB于X,
∵∠AGN=90°,AG=1,∠BAC=60°,
∴AI=2AG=2,
∴BI=BD=2,
∵∠ABC=60°,
∴△BDI是等边三角形,
∴XI=BX=1,
∵∠NIX=∠AIG=30°,∠IXN=90°,
∴IN,
∵GI=AG tan60°AG,
∴GN=GI+IN,
∴AM=GN,
∴S△AMCAM CD.
第7页(共17页)
同课章节目录
