2025年山东日照中考数学模拟试题(含解析)
文档属性
| 名称 | 2025年山东日照中考数学模拟试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-07 07:52:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年山东日照中考数学模拟试题
考试时间:120分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共12小题,满分36分,每小题3分)
1.下列运算结果是正数的是( )
A.3﹣1 B.﹣32 C.﹣|﹣3| D.
2.下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是( )
A.戴口罩讲卫生 B.勤洗手勤通风
C.有症状早就医 D.少出门少聚集
3.2024年6月25日嫦娥六号顺利返回地球,带回大约2kg的月背样本,实现世界首次月背采样返回,标志着我国对月球背面的研究又进入了一个新的高度.已知月球到地球的平均距离约为384000千米,数据384000用科学记数法表示为( )
A.384×103 B.38.4×104 C.3.84×105 D.0.384×106
4.如图,直线a∥b,将含有30°角的直角三角尺按如图所示的位置放置,若∠1=15°,那么∠2的大小为( )
A.60° B.55° C.45° D.35°
5.新能源汽车比传统燃油车具有静音、节能、智能等优势.如图是某新能源汽车公司2022年和2023年每个季度某种车型的出口销售额折线图,该公司的这种车型在2023年的每个季度都比2022年的同一季度增加相同的出口销售额,根据统计图,下列关于这两年该种车型的出口销售额的描述,正确的是( )
A.众数不变 B.中位数不变 C.平均数不变 D.方差不变
6.如图,小明在点C处测得树的顶端A仰角为α,同时测得AB=6m,则AC为( )m.
A.6sinα B. C.6tanα D.
7.方程x3﹣4x=0的解是( )
A.2或0 B.±2或0 C.2 D.﹣2或0
8.如图,在矩形ABCD中,AB=6,BC=8,点E在DC上,把△ADE沿AE折叠,点D恰好落在BC边上的点F处,则cos∠CEF的值为( )
A. B. C. D.
9.如图所示,正方形ABCD与AEFG(其中边BC,EF分别在x,y轴的正半轴上)的公共顶点A在反比例函数y的图象上,直线DG与x,y轴分别相交于点M,N.若这两个正方形的面积之和是,且MD=4GN.则k的值是( )
A.5 B.1 C.3 D.2
10.如图,设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车原地返回.设x小时后两车间的距离为y千米,y关于x的函数关系如图所示,则乙车的速度为( )
A.60千米/小时 B.70千米/小时
C.75千米/小时 D.80千米/小时
11.已知二次函数y=ax2+bx+c(a<0)的图象经过点(﹣1,0),对称轴为直线x=2,对于下列结论:①abc<0;②a+c=b;③多项式ax2+bx+c可因式分解为(x+1) (x﹣5);④当m>﹣9a时,关于x的方程ax2+bx+c=m无实数根.其中正确的是( )
A.①②③ B.②③④ C.①②④ D.①③④
12.问题:有一列数,按一定规律排成一列:1,﹣3,9,﹣27,81,﹣243……其中某三个相邻数的和是﹣1701,求这三个数中最小的数.
为解决问题,甲、乙两人给出各自为解题所设列的方程:
甲:设这三个数中绝对值最小的一个数是x,则另两个数依次是﹣3x、9x,根据题意得x﹣3x+9x=﹣1701.
乙:某三个相邻数的和是﹣1701,则设这三个数中绝对值最小的一个数是﹣3x﹣1,则另两个数依次是3x,﹣3x+1,根据题意得﹣3x﹣1+3x﹣3x+1=﹣1701.
下列说法正确的是( )
A.甲、乙两人所列方程都正确 B.甲、乙两人所列方程都不正确
C.甲列方程正确、乙列方程不正确 D.甲列方程不正确、乙列方程正确
二.填空题(共4小题,满分12分,每小题3分)
13.定义新运算※,对于任意实数a,b都有a※b=a2+ab,如果3※4=32+3×4=9+12=21,那么方程x※5=0的解为 .
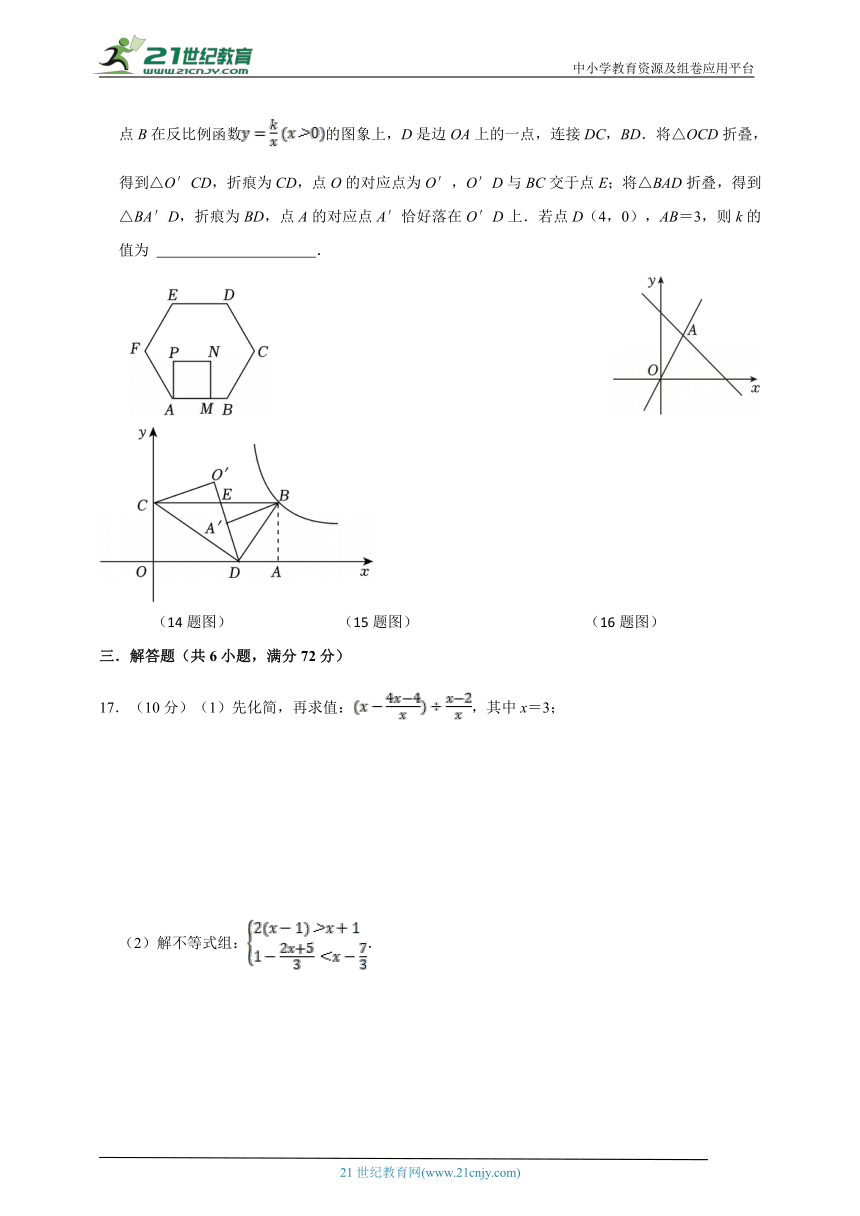
14.如图,正方形AMNP的边AM在正六边形ABCDEF的边AB上,则∠PAF= 度.
15.正比例函数 y =2 x 和一次函数 y = kx +5( k 为常数,且 k 不为0)的图象交于点 A ( m ,3),则关于 x 的不等式2 x < kx +5的解集为 .
16.如图,在平面直角坐标系中,矩形OABC的顶点与原点O重合,边OA在x轴上,OC在y轴上,点B在反比例函数的图象上,D是边OA上的一点,连接DC,BD.将△OCD折叠,得到△O′CD,折痕为CD,点O的对应点为O′,O′D与BC交于点E;将△BAD折叠,得到△BA′D,折痕为BD,点A的对应点A′恰好落在O′D上.若点D(4,0),AB=3,则k的值为 .
(14题图) (15题图) (16题图)
三.解答题(共6小题,满分72分)
17.(10分)(1)先化简,再求值:,其中x=3;
(2)解不等式组:.
18.(10分)为迎接建党一百周年,甲、乙两名同学进行了六次党史知识测试,部分成绩如图所示,已知甲、乙两名同学六次成绩的平均数相等.
(1)计算甲同学成绩的平均数,并补充完整乙同学成绩的折线统计图;
(2)若乙同学成绩的方差为S乙2=33.3,请计算甲同学成绩的方差,并比较哪个同学的成绩较稳定;
(3)甲同学成绩的中位数和众数分别记作a,b,乙同学成绩的众数记作c,在数a,b,c中随机抽取两个数,求抽到的两个数恰好相等的概率.
19.(12分)如图1和图2所示,在平行四边形ABCD中,点M为对角线AC上的一点,点N为边BC上的一点,且点A和点N关于直线BM对称.
(1)请用尺规作图的方法在图1中确定点M,N的位置(保留作图痕迹,不用写出作法);
(2)如图2所示,若∠ABC=60°,∠ACB=45°,AB=10.
①求B,M两点之间的距离;
②连接DN,请直接写出CN和DN的长为多少.
20.(12分)3月12日是植树节,某学校开展植树活动.学校用6000元购买了A,B两种树苗共150棵.已知一棵B种树苗是一棵A种树苗价格的2倍,且购买A种树苗与购买B种树苗费用相同.
(1)求购买一棵A种树苗、一棵B种树苗各需多少元?
(2)若学校还需购买A,B两种树苗共90棵,且A种树苗的棵数不多于B种树苗棵数的2倍,问至少要花多少钱?
21.(14分)如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A、D、B三点,CB的延长线交⊙O于点E,过点E作⊙O的切线,交AC的延长线于点F.
(1)求证:AE=CE;
(2)若CF=CD=2,求⊙O的半径和sin∠CAB的值;
(3)若CF=k CD(k>0),直接写出sin∠CAB的值(用含k的代数式表示).
22.(14分)平面直角坐标系中,抛物线y=ax2+bx+4与x轴交于A(﹣3,0),B(2,0)两点,与y轴交于点C,连接AC、BC.
(1)求抛物线y的函数表达式;
(2)如图1,点P为直线AC上方抛物线上一动点,过点P作 PD⊥AC于点D,过点P作PE∥AB交直线BC于E,求PDPE的最大值以及此时点P的坐标;
(3)如图2,将原抛物线y向右平移2个单位得到新抛物线y,在新抛物线y上找一点M,使得△MAC与△MAO的面积之比为5:3,请直接写出满足条件的所有点M的横坐标,并写出其中一个横坐标的求解过程.
参考答案
一.选择题(共12小题,满分36分,每小题3分)
1.解:A、0,此选项符合题意;
B、﹣32=﹣9<0,此选项不符合题意;
C、﹣|﹣3|=﹣3<0,此选项不符合题意;
D、,此选项不符合题意;
选:A.
2.解:A、是轴对称图形,不是中心对称图形,此选项不合题意;
B、不是轴对称图形,也不是中心对称图形,此选项不合题意;
C、既是中心对称图形也是轴对称图形,此选项符合题意;
D、不是轴对称图形,也不是中心对称图形,此选项不合题意;
选:C.
3.解:384000=3.84×105.
选:C.
4.解:
∵图中是一个含有30°角的直角三角尺,
∴∠1+∠4=60°,
∵∠1=15°,
∴∠4=60°﹣∠1=45°,
∵a∥b,
∴∠3=∠4=45°,
∵∠2+∠3+90°=180°,
∴∠2=180°﹣∠3﹣90°=180°﹣45°﹣90°=45°.
选:C.
5.解:∵该公司的这种车型在2023年的每个季度都比2022年的同一季度增加相同的出口销售额,
∴平均数,中位数,众数都会增加,但出口销售额的波动不会改变,
∴方差不变,
选:D.
6.解:在Rt△ABC中,AB=6m,∠ACB=α,sinα,
∴AC(m),
选:B.
7.解:x3﹣4x=0,
∴x(x2﹣4)=0.
∴x(x+2)(x﹣2)=0.
∴x=0或x+2=0或x﹣2=0.
∴x1=0,x2=﹣2,x3=2.
选:B.
8.解:方法一:∵四边形ABCD是矩形,
∴AD=BC=8,DC=AB=6,
∵把△ADE沿AE折叠,点D恰好落在BC边上的点F处,
∴AF=AD=8,EF=DE,
∴BF,
∴CF=BC﹣BF=8,
在Rt△EFC中,
CE=DC﹣DE=6﹣EF,
由勾股定理,得EF2=CE2+CF2,
∴EF2=(6﹣EF)2+(8)2,
∴EF,
∴CE=6,
∴cos∠CEF,
选:A.
方法二:∵四边形ABCD是矩形,
∴AD=BC=8,∠B=∠C=∠D=90°,
∴∠CEF+∠EFC=90°,
∵把△ADE沿AE折叠,点D恰好落在BC边上的点F处,
∴AF=AD=8,∠AFE=∠D=90°,
∴∠AFB+∠EFC=90°,
∴∠CEF=∠AFB,
∵AB=6,
∴BF,
∴cos∠CEF=cos∠AFB
选:A.
9.解:设AE=EF=FG=a,AB=BC=AD=b,
由题意得:a2+b2.
∵正方形ABCD与AEFG(其中边BC,EF分别在x,y轴的正半轴上)的公共顶点A在反比例函数y的图象上,
∴FG∥ED∥OM,∠NFG=∠DCM=90°,
∴∠NGF=∠DMC,
∴△NFG∽△DCM,
∴,
∵MD=4GN,
∴,
∴NFb.
∵FG∥ED,
∴△NFG∽△NED,
∴,
∴,
∴b2=4a2,
∴,
∵a>0,
∴a.
∴b.
∴A(,),
∴k3.
选:C.
10.解:设甲车的速度为a千米/小时,乙车的速度为b千米/小时,
由图可得:,
解得,
即甲车的速度为60千米/小时,乙车的速度为70千米/小时,
选:B.
11.解:由题意得,a<0.
又∵对称轴是直线x2,
∴b=﹣4a>0.
∵x=﹣1时,y=0,
∴a﹣b+c=0,
∴a+c=b,c=b﹣a=﹣5a>0,②正确.
∴abc<0,①正确.
∵函数图象经过点(﹣1,0),对称轴为直线x=2,
∴抛物线与x轴的另一个交点为(5,0),
∴多项式ax2+bx+c可因式分解为a(x+1) (x﹣5),③错误,
∵抛物线的解析式为y=a(x+1)(x﹣5)=a(x2﹣4x﹣5)=a(x﹣2)2﹣9a,
∴抛物线的顶点坐标为(2,﹣9a),
∴当m>﹣9a时,关于x的方程ax2+bx+c=m无实数根,④正确.
综上,正确的是①②④.
选:C.
12.解:解法一:设这三个数中绝对值最小的一个数是x,则另两个数依次是﹣3x、9x,根据题意得x﹣3x+9x=﹣1701.甲所列方程正确;
乙:解法二:设这三个数中绝对值最小的一个数是﹣3x﹣1,则另两个数依次是3x,﹣3x+1,根据题意得﹣3x﹣1+3x﹣3x+1=﹣1701.乙所列方程正确.
选:A.
二.填空题(共4小题,满分12分,每小题3分)
13.解:x※5=0,
则x2+5x=0,
x(x+5)=0,
解得:x=0或﹣5.
答案为:0或﹣5.
14.解:由题意可知,∠BAF=(n﹣2)×180°÷6=120°,∠PAM=90°,
∴∠PAF=∠BAF﹣∠PAM=30°.
答案为:30.
15.解:把A(m,3)代入y=2x得2m=3,解得m,
∴A(,3),
由图象可知,当x时,2x<kx+5,
关于 x 的不等式2 x < kx +5的解集为x.
答案为:x.
16.解:由轴对称的性质可知,∠CDO′,∠A′DB,
∵∠ODO′+∠ADA′=180°,
∴∠CDO′+∠A′DB=90°,
∴△BCD是Rt△,
∴BC2=CD2+BD2,
设BC=OA=m,
∵AB=3,D(4,0),
∴OC=AB=3,OD=4,
∴AD=m﹣4,
∴CD2=OC2+OD2=25,BD2=AD2+AB2=(m﹣4)2+32,
∴BC2=OC2+OD2+AD2+AB2,
∴m2=25+(m﹣4)2+9,
解得m,
∴B(,3),
∵点B在反比例函数的图象上,
∴k.
答案为:.
三.解答题(共6小题,满分72分)
17.解:(1)原式
=x﹣2,
当x=3时,
原式=3﹣2
=1;
(2),
解不等式①得:x>3;
解不等式②得:x>1,
∴不等式组的解集为x>3.
18.解:(1)∵,
则75×6﹣80﹣70﹣70﹣75﹣70=85,
补充完整乙同学成绩的折线统计图如下:
(2)S乙2,
∵甲、乙两名同学六次成绩的平均数相同,,
∴乙同学成绩较稳定;
(3)∵甲成绩的中位数为,众数为75,乙成绩的众数为70,
∴a=75,b=75,c=70,
列表如下:
75 75 70
75 (75,75) (75,70)
75 (75,75) (75,70)
70 (70,75) (70,75)
共有6种等可能的结果,抽到的两个数恰好相等的结果有2种,
∴抽到的两个数恰好相等的概率为.
19.解:(1)如图1,以AB为半径作弧交BC于点N,再作∠ABC的平分线交AC于点M,
点M、N就是所要确定的点;
(2)①如图2,连接BM,AN,
∵点A,N关于直线BM对称,
∴BM是AN的中垂线,
∴BN=BA,
则,
∴∠BMA=∠MBC+∠ACB=30°+45°=75°,
又∵∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣60°﹣45°=75°,
∴∠BMA=∠BAC,
∴,
即B,M两点之间的距离为;
②如图3,过A作AF⊥BC于点F,
由①可知,BN=BA,
∵∠ABC=60°,
∴△ABN是等边三角形,
∴AN=BN=AB=10,
∵AF⊥BC,
∴∠AFB=∠AFC=90°,BF=FNBN=5,
∴AF15,
∵∠ACB=45°,
∴△ACF是等腰直角三角形,
∴CF=AF=15,ACAF=15,
∴BC=BF+CF=515,
∴CN=BC﹣BN=515﹣1015﹣5,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∵AN=AB,
∴AN=CD,
∴四边形ANCD是等腰梯形,
∴DN=AC=15,
即CN的长为15﹣5,DN的长为15.
20.解:(1)设购买一棵A种树苗需要x元,则购买一棵B种树苗需要2x元,
依题意得:150,
解得:x=30,
经检验,x=30是原方程的解,且符合题意,
∴2x=2×30=60.
答:购买一棵B种树苗需要60元,购买一棵A种树苗需要30元.
(2)设购买A种树苗m棵,则购买B种树苗(90﹣m)棵,
依题意得:m≤2(90﹣m),
解得:m≤60.
设购买两种树苗80棵所需总费用为w元,则w=30m+60(90﹣m)=﹣30m+5400.
∵﹣30<0,
∴w随m的增大而减小,
又∵m≤60,且m为正整数,
∴当m60时,w取得最小值,最小值=﹣30×60+5400=3600.
答:至少要花3600元钱.
21.证明:(1)连接DE,
∵∠ABC=90°,
∴∠ABE=90°,
∴AE是⊙O直径
∴∠ADE=90°,即DE⊥AC,
又∵D是AC的中点,
∴DE是AC的垂直平分线,
∴AE=CE;
(2)在△ADE和△EFA中,
∵∠ADE=∠AEF=90°,∠DAE=∠EAF,
∴△ADE∽△AEF,
∴,即,
解得:AE=2cm;
即⊙O的直径为2cm,
∴⊙O的半径为cm;
∵∠ADE=∠FDE=∠AEF=90°,
∴∠DAE+∠AED=∠FED+∠AED=90°,
∴∠DAE=∠DEF,
∴△ADE∽△EDF,
∴,
∴DE2=AD DF=2×4=8,
∴DE=2,
在Rt△CDE中,CE2,
∴sin∠CED,
∵∠CAB=∠CED,
∴sin∠CAB;
(3)∵AE=CE,
∴∠DAE=∠ACB,
∵∠CAB+∠ACB=90°,∠DEA+∠DAE=90°,
∴∠CAB=∠DEA,
∵CF=k CD,点D是AC中点,
∴DF=(k+1)CD,
∵△ADE∽△EDF,
∴,
∴DE2=AD DF=(k+1)CD2,
∴DECD,
在Rt△CDE中,CECD,
∴sin∠CED,
∵∠CAB=∠CED,
∴sin∠CAB.
22.解:(1)设抛物线的解析式为:y=a(x+3)(x﹣2),
将点C(0,4)代入得,
4=a 3×(﹣2),
∴a,
∴y;
(2)如图1,
设AC与EP交于点F,
∵A(﹣3,0),C(0,4),B(2,0),
∴直线AC的解析式为:y,直线BC的解析式为:y=﹣2x+4,AC=5,
∴sin∠PFD=sin∠CAO
设P(t,),
由﹣2x+4
x,
∴PE,
∴,
由得,
x,
∴PF,
∴PD=PF sin∠PFD=PF sin∠CAO(),
∴PD,
∴当t时,(PD)最大,
当t时,,
∴P();
(3)如图2,
作MV⊥AC于V,作MW⊥AB,交AC于W,
∵点A和点B香油平移2个单位后坐标分别是(﹣1,0),(4,0),
∴新抛物线的解析式为:y(x+1)(x﹣4),
设M(m,),
∴W(m,),
∴WM=||,
∴MV=WM sin∠ACO||=||
∴S△MAOOA |yM|||=|m2﹣3m﹣4|,
S△MAC|m2﹣m+2|,
∵△MAC与△MAO的面积之比为5:3,
∴5|m2﹣3m﹣4|=3|m2﹣m+2|,
∴m1=3,m2=3,m3,m4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2025年山东日照中考数学模拟试题
考试时间:120分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共12小题,满分36分,每小题3分)
1.下列运算结果是正数的是( )
A.3﹣1 B.﹣32 C.﹣|﹣3| D.
2.下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是( )
A.戴口罩讲卫生 B.勤洗手勤通风
C.有症状早就医 D.少出门少聚集
3.2024年6月25日嫦娥六号顺利返回地球,带回大约2kg的月背样本,实现世界首次月背采样返回,标志着我国对月球背面的研究又进入了一个新的高度.已知月球到地球的平均距离约为384000千米,数据384000用科学记数法表示为( )
A.384×103 B.38.4×104 C.3.84×105 D.0.384×106
4.如图,直线a∥b,将含有30°角的直角三角尺按如图所示的位置放置,若∠1=15°,那么∠2的大小为( )
A.60° B.55° C.45° D.35°
5.新能源汽车比传统燃油车具有静音、节能、智能等优势.如图是某新能源汽车公司2022年和2023年每个季度某种车型的出口销售额折线图,该公司的这种车型在2023年的每个季度都比2022年的同一季度增加相同的出口销售额,根据统计图,下列关于这两年该种车型的出口销售额的描述,正确的是( )
A.众数不变 B.中位数不变 C.平均数不变 D.方差不变
6.如图,小明在点C处测得树的顶端A仰角为α,同时测得AB=6m,则AC为( )m.
A.6sinα B. C.6tanα D.
7.方程x3﹣4x=0的解是( )
A.2或0 B.±2或0 C.2 D.﹣2或0
8.如图,在矩形ABCD中,AB=6,BC=8,点E在DC上,把△ADE沿AE折叠,点D恰好落在BC边上的点F处,则cos∠CEF的值为( )
A. B. C. D.
9.如图所示,正方形ABCD与AEFG(其中边BC,EF分别在x,y轴的正半轴上)的公共顶点A在反比例函数y的图象上,直线DG与x,y轴分别相交于点M,N.若这两个正方形的面积之和是,且MD=4GN.则k的值是( )
A.5 B.1 C.3 D.2
10.如图,设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车原地返回.设x小时后两车间的距离为y千米,y关于x的函数关系如图所示,则乙车的速度为( )
A.60千米/小时 B.70千米/小时
C.75千米/小时 D.80千米/小时
11.已知二次函数y=ax2+bx+c(a<0)的图象经过点(﹣1,0),对称轴为直线x=2,对于下列结论:①abc<0;②a+c=b;③多项式ax2+bx+c可因式分解为(x+1) (x﹣5);④当m>﹣9a时,关于x的方程ax2+bx+c=m无实数根.其中正确的是( )
A.①②③ B.②③④ C.①②④ D.①③④
12.问题:有一列数,按一定规律排成一列:1,﹣3,9,﹣27,81,﹣243……其中某三个相邻数的和是﹣1701,求这三个数中最小的数.
为解决问题,甲、乙两人给出各自为解题所设列的方程:
甲:设这三个数中绝对值最小的一个数是x,则另两个数依次是﹣3x、9x,根据题意得x﹣3x+9x=﹣1701.
乙:某三个相邻数的和是﹣1701,则设这三个数中绝对值最小的一个数是﹣3x﹣1,则另两个数依次是3x,﹣3x+1,根据题意得﹣3x﹣1+3x﹣3x+1=﹣1701.
下列说法正确的是( )
A.甲、乙两人所列方程都正确 B.甲、乙两人所列方程都不正确
C.甲列方程正确、乙列方程不正确 D.甲列方程不正确、乙列方程正确
二.填空题(共4小题,满分12分,每小题3分)
13.定义新运算※,对于任意实数a,b都有a※b=a2+ab,如果3※4=32+3×4=9+12=21,那么方程x※5=0的解为 .
14.如图,正方形AMNP的边AM在正六边形ABCDEF的边AB上,则∠PAF= 度.
15.正比例函数 y =2 x 和一次函数 y = kx +5( k 为常数,且 k 不为0)的图象交于点 A ( m ,3),则关于 x 的不等式2 x < kx +5的解集为 .
16.如图,在平面直角坐标系中,矩形OABC的顶点与原点O重合,边OA在x轴上,OC在y轴上,点B在反比例函数的图象上,D是边OA上的一点,连接DC,BD.将△OCD折叠,得到△O′CD,折痕为CD,点O的对应点为O′,O′D与BC交于点E;将△BAD折叠,得到△BA′D,折痕为BD,点A的对应点A′恰好落在O′D上.若点D(4,0),AB=3,则k的值为 .
(14题图) (15题图) (16题图)
三.解答题(共6小题,满分72分)
17.(10分)(1)先化简,再求值:,其中x=3;
(2)解不等式组:.
18.(10分)为迎接建党一百周年,甲、乙两名同学进行了六次党史知识测试,部分成绩如图所示,已知甲、乙两名同学六次成绩的平均数相等.
(1)计算甲同学成绩的平均数,并补充完整乙同学成绩的折线统计图;
(2)若乙同学成绩的方差为S乙2=33.3,请计算甲同学成绩的方差,并比较哪个同学的成绩较稳定;
(3)甲同学成绩的中位数和众数分别记作a,b,乙同学成绩的众数记作c,在数a,b,c中随机抽取两个数,求抽到的两个数恰好相等的概率.
19.(12分)如图1和图2所示,在平行四边形ABCD中,点M为对角线AC上的一点,点N为边BC上的一点,且点A和点N关于直线BM对称.
(1)请用尺规作图的方法在图1中确定点M,N的位置(保留作图痕迹,不用写出作法);
(2)如图2所示,若∠ABC=60°,∠ACB=45°,AB=10.
①求B,M两点之间的距离;
②连接DN,请直接写出CN和DN的长为多少.
20.(12分)3月12日是植树节,某学校开展植树活动.学校用6000元购买了A,B两种树苗共150棵.已知一棵B种树苗是一棵A种树苗价格的2倍,且购买A种树苗与购买B种树苗费用相同.
(1)求购买一棵A种树苗、一棵B种树苗各需多少元?
(2)若学校还需购买A,B两种树苗共90棵,且A种树苗的棵数不多于B种树苗棵数的2倍,问至少要花多少钱?
21.(14分)如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A、D、B三点,CB的延长线交⊙O于点E,过点E作⊙O的切线,交AC的延长线于点F.
(1)求证:AE=CE;
(2)若CF=CD=2,求⊙O的半径和sin∠CAB的值;
(3)若CF=k CD(k>0),直接写出sin∠CAB的值(用含k的代数式表示).
22.(14分)平面直角坐标系中,抛物线y=ax2+bx+4与x轴交于A(﹣3,0),B(2,0)两点,与y轴交于点C,连接AC、BC.
(1)求抛物线y的函数表达式;
(2)如图1,点P为直线AC上方抛物线上一动点,过点P作 PD⊥AC于点D,过点P作PE∥AB交直线BC于E,求PDPE的最大值以及此时点P的坐标;
(3)如图2,将原抛物线y向右平移2个单位得到新抛物线y,在新抛物线y上找一点M,使得△MAC与△MAO的面积之比为5:3,请直接写出满足条件的所有点M的横坐标,并写出其中一个横坐标的求解过程.
参考答案
一.选择题(共12小题,满分36分,每小题3分)
1.解:A、0,此选项符合题意;
B、﹣32=﹣9<0,此选项不符合题意;
C、﹣|﹣3|=﹣3<0,此选项不符合题意;
D、,此选项不符合题意;
选:A.
2.解:A、是轴对称图形,不是中心对称图形,此选项不合题意;
B、不是轴对称图形,也不是中心对称图形,此选项不合题意;
C、既是中心对称图形也是轴对称图形,此选项符合题意;
D、不是轴对称图形,也不是中心对称图形,此选项不合题意;
选:C.
3.解:384000=3.84×105.
选:C.
4.解:
∵图中是一个含有30°角的直角三角尺,
∴∠1+∠4=60°,
∵∠1=15°,
∴∠4=60°﹣∠1=45°,
∵a∥b,
∴∠3=∠4=45°,
∵∠2+∠3+90°=180°,
∴∠2=180°﹣∠3﹣90°=180°﹣45°﹣90°=45°.
选:C.
5.解:∵该公司的这种车型在2023年的每个季度都比2022年的同一季度增加相同的出口销售额,
∴平均数,中位数,众数都会增加,但出口销售额的波动不会改变,
∴方差不变,
选:D.
6.解:在Rt△ABC中,AB=6m,∠ACB=α,sinα,
∴AC(m),
选:B.
7.解:x3﹣4x=0,
∴x(x2﹣4)=0.
∴x(x+2)(x﹣2)=0.
∴x=0或x+2=0或x﹣2=0.
∴x1=0,x2=﹣2,x3=2.
选:B.
8.解:方法一:∵四边形ABCD是矩形,
∴AD=BC=8,DC=AB=6,
∵把△ADE沿AE折叠,点D恰好落在BC边上的点F处,
∴AF=AD=8,EF=DE,
∴BF,
∴CF=BC﹣BF=8,
在Rt△EFC中,
CE=DC﹣DE=6﹣EF,
由勾股定理,得EF2=CE2+CF2,
∴EF2=(6﹣EF)2+(8)2,
∴EF,
∴CE=6,
∴cos∠CEF,
选:A.
方法二:∵四边形ABCD是矩形,
∴AD=BC=8,∠B=∠C=∠D=90°,
∴∠CEF+∠EFC=90°,
∵把△ADE沿AE折叠,点D恰好落在BC边上的点F处,
∴AF=AD=8,∠AFE=∠D=90°,
∴∠AFB+∠EFC=90°,
∴∠CEF=∠AFB,
∵AB=6,
∴BF,
∴cos∠CEF=cos∠AFB
选:A.
9.解:设AE=EF=FG=a,AB=BC=AD=b,
由题意得:a2+b2.
∵正方形ABCD与AEFG(其中边BC,EF分别在x,y轴的正半轴上)的公共顶点A在反比例函数y的图象上,
∴FG∥ED∥OM,∠NFG=∠DCM=90°,
∴∠NGF=∠DMC,
∴△NFG∽△DCM,
∴,
∵MD=4GN,
∴,
∴NFb.
∵FG∥ED,
∴△NFG∽△NED,
∴,
∴,
∴b2=4a2,
∴,
∵a>0,
∴a.
∴b.
∴A(,),
∴k3.
选:C.
10.解:设甲车的速度为a千米/小时,乙车的速度为b千米/小时,
由图可得:,
解得,
即甲车的速度为60千米/小时,乙车的速度为70千米/小时,
选:B.
11.解:由题意得,a<0.
又∵对称轴是直线x2,
∴b=﹣4a>0.
∵x=﹣1时,y=0,
∴a﹣b+c=0,
∴a+c=b,c=b﹣a=﹣5a>0,②正确.
∴abc<0,①正确.
∵函数图象经过点(﹣1,0),对称轴为直线x=2,
∴抛物线与x轴的另一个交点为(5,0),
∴多项式ax2+bx+c可因式分解为a(x+1) (x﹣5),③错误,
∵抛物线的解析式为y=a(x+1)(x﹣5)=a(x2﹣4x﹣5)=a(x﹣2)2﹣9a,
∴抛物线的顶点坐标为(2,﹣9a),
∴当m>﹣9a时,关于x的方程ax2+bx+c=m无实数根,④正确.
综上,正确的是①②④.
选:C.
12.解:解法一:设这三个数中绝对值最小的一个数是x,则另两个数依次是﹣3x、9x,根据题意得x﹣3x+9x=﹣1701.甲所列方程正确;
乙:解法二:设这三个数中绝对值最小的一个数是﹣3x﹣1,则另两个数依次是3x,﹣3x+1,根据题意得﹣3x﹣1+3x﹣3x+1=﹣1701.乙所列方程正确.
选:A.
二.填空题(共4小题,满分12分,每小题3分)
13.解:x※5=0,
则x2+5x=0,
x(x+5)=0,
解得:x=0或﹣5.
答案为:0或﹣5.
14.解:由题意可知,∠BAF=(n﹣2)×180°÷6=120°,∠PAM=90°,
∴∠PAF=∠BAF﹣∠PAM=30°.
答案为:30.
15.解:把A(m,3)代入y=2x得2m=3,解得m,
∴A(,3),
由图象可知,当x时,2x<kx+5,
关于 x 的不等式2 x < kx +5的解集为x.
答案为:x.
16.解:由轴对称的性质可知,∠CDO′,∠A′DB,
∵∠ODO′+∠ADA′=180°,
∴∠CDO′+∠A′DB=90°,
∴△BCD是Rt△,
∴BC2=CD2+BD2,
设BC=OA=m,
∵AB=3,D(4,0),
∴OC=AB=3,OD=4,
∴AD=m﹣4,
∴CD2=OC2+OD2=25,BD2=AD2+AB2=(m﹣4)2+32,
∴BC2=OC2+OD2+AD2+AB2,
∴m2=25+(m﹣4)2+9,
解得m,
∴B(,3),
∵点B在反比例函数的图象上,
∴k.
答案为:.
三.解答题(共6小题,满分72分)
17.解:(1)原式
=x﹣2,
当x=3时,
原式=3﹣2
=1;
(2),
解不等式①得:x>3;
解不等式②得:x>1,
∴不等式组的解集为x>3.
18.解:(1)∵,
则75×6﹣80﹣70﹣70﹣75﹣70=85,
补充完整乙同学成绩的折线统计图如下:
(2)S乙2,
∵甲、乙两名同学六次成绩的平均数相同,,
∴乙同学成绩较稳定;
(3)∵甲成绩的中位数为,众数为75,乙成绩的众数为70,
∴a=75,b=75,c=70,
列表如下:
75 75 70
75 (75,75) (75,70)
75 (75,75) (75,70)
70 (70,75) (70,75)
共有6种等可能的结果,抽到的两个数恰好相等的结果有2种,
∴抽到的两个数恰好相等的概率为.
19.解:(1)如图1,以AB为半径作弧交BC于点N,再作∠ABC的平分线交AC于点M,
点M、N就是所要确定的点;
(2)①如图2,连接BM,AN,
∵点A,N关于直线BM对称,
∴BM是AN的中垂线,
∴BN=BA,
则,
∴∠BMA=∠MBC+∠ACB=30°+45°=75°,
又∵∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣60°﹣45°=75°,
∴∠BMA=∠BAC,
∴,
即B,M两点之间的距离为;
②如图3,过A作AF⊥BC于点F,
由①可知,BN=BA,
∵∠ABC=60°,
∴△ABN是等边三角形,
∴AN=BN=AB=10,
∵AF⊥BC,
∴∠AFB=∠AFC=90°,BF=FNBN=5,
∴AF15,
∵∠ACB=45°,
∴△ACF是等腰直角三角形,
∴CF=AF=15,ACAF=15,
∴BC=BF+CF=515,
∴CN=BC﹣BN=515﹣1015﹣5,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∵AN=AB,
∴AN=CD,
∴四边形ANCD是等腰梯形,
∴DN=AC=15,
即CN的长为15﹣5,DN的长为15.
20.解:(1)设购买一棵A种树苗需要x元,则购买一棵B种树苗需要2x元,
依题意得:150,
解得:x=30,
经检验,x=30是原方程的解,且符合题意,
∴2x=2×30=60.
答:购买一棵B种树苗需要60元,购买一棵A种树苗需要30元.
(2)设购买A种树苗m棵,则购买B种树苗(90﹣m)棵,
依题意得:m≤2(90﹣m),
解得:m≤60.
设购买两种树苗80棵所需总费用为w元,则w=30m+60(90﹣m)=﹣30m+5400.
∵﹣30<0,
∴w随m的增大而减小,
又∵m≤60,且m为正整数,
∴当m60时,w取得最小值,最小值=﹣30×60+5400=3600.
答:至少要花3600元钱.
21.证明:(1)连接DE,
∵∠ABC=90°,
∴∠ABE=90°,
∴AE是⊙O直径
∴∠ADE=90°,即DE⊥AC,
又∵D是AC的中点,
∴DE是AC的垂直平分线,
∴AE=CE;
(2)在△ADE和△EFA中,
∵∠ADE=∠AEF=90°,∠DAE=∠EAF,
∴△ADE∽△AEF,
∴,即,
解得:AE=2cm;
即⊙O的直径为2cm,
∴⊙O的半径为cm;
∵∠ADE=∠FDE=∠AEF=90°,
∴∠DAE+∠AED=∠FED+∠AED=90°,
∴∠DAE=∠DEF,
∴△ADE∽△EDF,
∴,
∴DE2=AD DF=2×4=8,
∴DE=2,
在Rt△CDE中,CE2,
∴sin∠CED,
∵∠CAB=∠CED,
∴sin∠CAB;
(3)∵AE=CE,
∴∠DAE=∠ACB,
∵∠CAB+∠ACB=90°,∠DEA+∠DAE=90°,
∴∠CAB=∠DEA,
∵CF=k CD,点D是AC中点,
∴DF=(k+1)CD,
∵△ADE∽△EDF,
∴,
∴DE2=AD DF=(k+1)CD2,
∴DECD,
在Rt△CDE中,CECD,
∴sin∠CED,
∵∠CAB=∠CED,
∴sin∠CAB.
22.解:(1)设抛物线的解析式为:y=a(x+3)(x﹣2),
将点C(0,4)代入得,
4=a 3×(﹣2),
∴a,
∴y;
(2)如图1,
设AC与EP交于点F,
∵A(﹣3,0),C(0,4),B(2,0),
∴直线AC的解析式为:y,直线BC的解析式为:y=﹣2x+4,AC=5,
∴sin∠PFD=sin∠CAO
设P(t,),
由﹣2x+4
x,
∴PE,
∴,
由得,
x,
∴PF,
∴PD=PF sin∠PFD=PF sin∠CAO(),
∴PD,
∴当t时,(PD)最大,
当t时,,
∴P();
(3)如图2,
作MV⊥AC于V,作MW⊥AB,交AC于W,
∵点A和点B香油平移2个单位后坐标分别是(﹣1,0),(4,0),
∴新抛物线的解析式为:y(x+1)(x﹣4),
设M(m,),
∴W(m,),
∴WM=||,
∴MV=WM sin∠ACO||=||
∴S△MAOOA |yM|||=|m2﹣3m﹣4|,
S△MAC|m2﹣m+2|,
∵△MAC与△MAO的面积之比为5:3,
∴5|m2﹣3m﹣4|=3|m2﹣m+2|,
∴m1=3,m2=3,m3,m4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
