2025年山东淮坊中考数学模拟试题(含解析)
文档属性
| 名称 | 2025年山东淮坊中考数学模拟试题(含解析) | 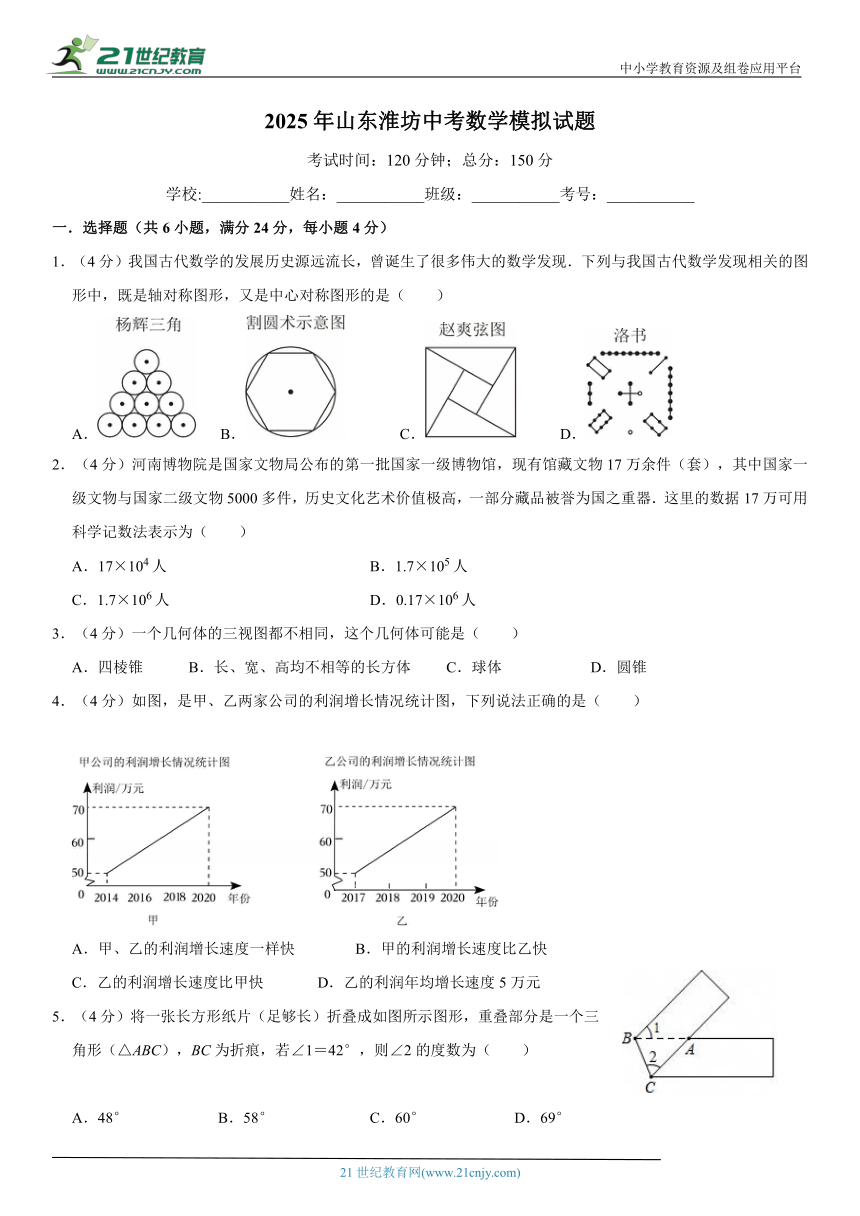 | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-07 18:56:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年山东淮坊中考数学模拟试题
考试时间:120分钟;总分:150分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共6小题,满分24分,每小题4分)
1.(4分)我国古代数学的发展历史源远流长,曾诞生了很多伟大的数学发现.下列与我国古代数学发现相关的图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.(4分)河南博物院是国家文物局公布的第一批国家一级博物馆,现有馆藏文物17万余件(套),其中国家一级文物与国家二级文物5000多件,历史文化艺术价值极高,一部分藏品被誉为国之重器.这里的数据17万可用科学记数法表示为( )
A.17×104人 B.1.7×105人
C.1.7×106人 D.0.17×106人
3.(4分)一个几何体的三视图都不相同,这个几何体可能是( )
A.四棱锥 B.长、宽、高均不相等的长方体 C.球体 D.圆锥
4.(4分)如图,是甲、乙两家公司的利润增长情况统计图,下列说法正确的是( )
A.甲、乙的利润增长速度一样快 B.甲的利润增长速度比乙快
C.乙的利润增长速度比甲快 D.乙的利润年均增长速度5万元
5.(4分)将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形(△ABC),BC为折痕,若∠1=42°,则∠2的度数为( )
A.48° B.58° C.60° D.69°
6.(4分)若关于x的一元二次方程x2﹣2x+a﹣1=0没有实数根,则a的取值范围是( )
A.a<2 B.a>2 C.a<﹣2 D.a>﹣2
二.多选题(共4小题,满分20分,每小题5分)
(多选)7.(5分)下列命题中正确的是( )
A.121的平方根是±11 B.两个无理数之和一定是无理数
C.实数不是有理数就是无理数 D.带根号的数一定是无理数
(多选)8.(5分)已知抛物线y=ax2+bx+c交x轴于点B(1,0)和点A,交y轴负半轴于点C,且AO=2CO.下列选项正确的是( )
A.2b+2c=﹣1 B.
C. D.4ac+2b+1=0
(多选)9.(5分)如图,△ABC内接于⊙O,BD为⊙O的直径,A为的中点,∠BAC=120°,连接AD、BC交于点E,则下列结论正确的是( )
A.AD=BC B.BE=3CE
C.点A、C为的三等分点 D.连接OC,则四边形ABOC为菱形
(多选)10.(5分)如图,⊙O是△ABC的外接圆,AO∥BC,连接CO并延长交⊙O于点D.分别以点A,C为圆心,以大于的长为半径作弧,并使两弧交于圆外一点M.直线OM交BC于点E,连接AE,下列结论一定正确的是( )
A. B.AB=OE
C.∠AOD=∠BAC D.四边形AOCE为菱形
三.填空题(共4小题,满分16分,每小题4分)
11.(4分)定义:如果函数图象上的一个点向左平移n个单位,再向上平移2(n+1)个单位后仍在这个函数图象上,我们称这个函数是“可回旋”函数,n称为这个函数的“可回旋单位”.如果y=﹣6x是“可回旋”函数,那么这个函数的“可回旋单位”是 .
12.(4分)如图,已知OD为等边△OAC的高,顶点O(0,0),D(1,1),若△OAC绕点O逆时针旋转,每秒旋转45°,则第60秒时,D点坐标为 .
13.(4分)某超市有A,B,C三种型号的甲种品牌饮水机和D,E两种型号的乙种品牌饮水机,某中学准备从甲、乙两种品牌的饮水机中各选购一种型号的饮水机安装到教室.如果各种选购方案被选中的可能性相同,那么A型号饮水机被选中的概率是 .
14.(4分)图中各正方形中的四个数之间都有相同的规律,则根据这种规律,第四个正方形中的n与最后一个正方形中的m之和,n+m= .
四.解答题(共8小题,满分90分)
15.(10分)(1)计算:()﹣1+(﹣5)×||;
(2)先化简,再求值:(1),其中a=2.
16.(10分)如图,在矩形ABCD中,M,N是对角线AC上的两点,将矩形折叠分别使点B与点M重合,点D与点N重合,折痕分别为AE,CF.连接EF,交AC于点O.
(1)求证:△ABE≌△CDF.
(2)求证:四边形ECFA是平行四边形.
17.(10分)如图,在平面直角坐标系中,一次函数y=k1x+b的图象与反比例函数的图象的两个交点为A(﹣1,3)和B.
(1)求反比例函数的关系式;
(2)若一次函数y=k1x+b与x轴交于点C,且;
①求出k1与b的值;
②直接写出不等式k1x+b的解集为 ;
(3)在(2)的基础上,若点F是直线OA上一点,F点的横坐标为m,连接AF,BF,△ABF的面积记为S,当S=2时,请直接写出m值 .
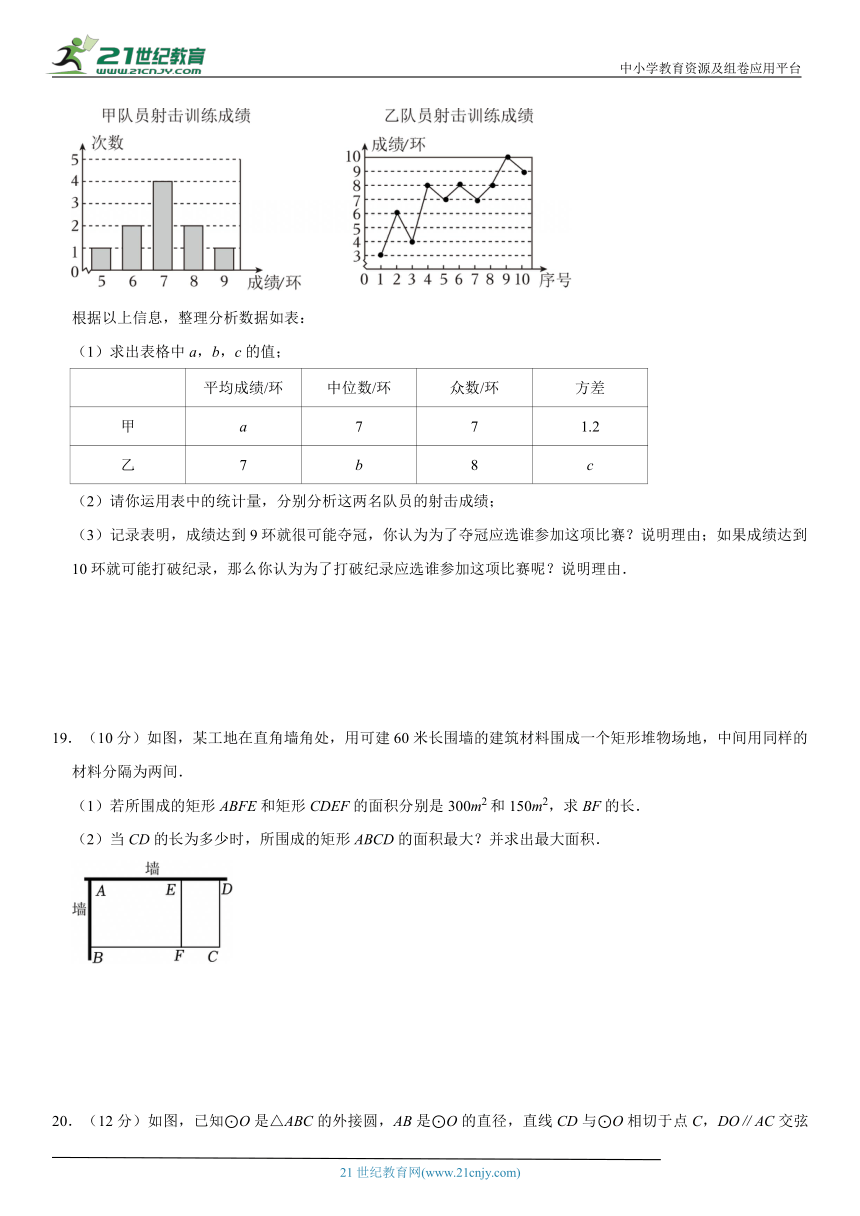
18.(11分)甲、乙两名队员参加射击训练(各射击10次),成绩分别被制成下列两个统计图(如图).
根据以上信息,整理分析数据如表:
(1)求出表格中a,b,c的值;
平均成绩/环 中位数/环 众数/环 方差
甲 a 7 7 1.2
乙 7 b 8 c
(2)请你运用表中的统计量,分别分析这两名队员的射击成绩;
(3)记录表明,成绩达到9环就很可能夺冠,你认为为了夺冠应选谁参加这项比赛?说明理由;如果成绩达到10环就可能打破纪录,那么你认为为了打破纪录应选谁参加这项比赛呢?说明理由.
19.(10分)如图,某工地在直角墙角处,用可建60米长围墙的建筑材料围成一个矩形堆物场地,中间用同样的材料分隔为两间.
(1)若所围成的矩形ABFE和矩形CDEF的面积分别是300m2和150m2,求BF的长.
(2)当CD的长为多少时,所围成的矩形ABCD的面积最大?并求出最大面积.
20.(12分)如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,直线CD与⊙O相切于点C,DO∥AC交弦BC于点F,交优弧于点E,连接BD,BE.
(1)求证:BD是⊙O的切线;
(2)若,AC=4,求OD的长.
21.(14分)如图,抛物线y=ax2﹣4ax+3a交x轴于A,B两点(点A在点B的左边),交y轴正半轴于点C,OB=OC,点P在抛物线上.
(1)求抛物线的解析式;
(2)平面上有两点M(m,﹣m﹣3),N(m+2,﹣m﹣5),求△PMN的面积的最小值;
(3)若tan∠APC,求点P的横坐标.
22.(13分)在平面直角坐标系xOy中,对于点P和半径为1的⊙C给出如下定义:若过点P的直线l交⊙C于A,B两点,在P,A,B三点中,其中一点恰为以另外两点为端点的线段中点时,则称点P为⊙C的关联点.
(1)当点C与O重合时,
①在点,E(4,0)中,⊙C的关联点是 ;
②已知点P(m,n)在直线y=﹣x+3上,若点P为⊙C的关联点,求m的取值范围;
(2)⊙C的圆心C(c,0),直线与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的关联点P,则c的取值范围是 .
参考答案
一.选择题(共6小题,满分24分,每小题4分)
1.解:A.是轴对称图形,不是中心对称图形,不符合题意.
B.既是轴对称图形,又是中心对称图形,符合题意.
C.是中心对称图形,不是轴对称图形,不符合题意.
D.既不是轴对称图形,也不是中心对称图形,不符合题意.
选:B.
2.解:17万=1.7×105,
选:B.
3.解:A,四棱锥的左视图和主视图都是三角形,不合题意;
B,长、宽、高均不相等的长方体的三视图都是长方形,但长、宽不同,符合题意;
C,球体的三视图都是圆形,不合题意;
D,圆锥的左视图和主视图都是三角形,不合题意;
选:B.
4.解:由图知,甲利润6年时间从50万增加到70万,而乙利润3年时间从50万增加到70万,
所以乙的利润增长速度比甲快,
选:C.
5.解:如图所示,
∵长方形的两条长边平行,∠1=42°,
∴∠1=∠4=42°,∠4=∠5,
∴∠5=42°,
由折叠的性质可知,∠2=∠3,
∵∠2+∠3+∠5=180°,
∴∠2=69°,
选:D.
6.解:由题意可知:Δ=4﹣4(a﹣1)<0,
∴a>2,
选:B.
二.多选题(共4小题,满分20分,每小题5分)
7.解:A.121的平方根是±11,正确,符合题意;
B.两个无理数之和不一定是无理数,错误,不符合题意;
C.实数不是有理数就是无理数,正确,符合题意;
D.带根号的数不一定是无理数,错误,不符合题意.
选:AC.
8.解:由抛物线的位置可知,a>0,b>0,c<0,因此<0,C不正确;
抛物线y=ax2+bx+c过点B (1,0),因此有a+b+c=0,
抛物线与y轴的交点C(0,c),
∵OA=2OC,
∴点A(2c,0),代入抛物线关系式得,4ac2+2bc+c=0,即4ac+2b+1=0,因此D正确;
∵点A(2c,0),B(1,0),
∴对称轴x,即4ac+2a+2b=0,
所以﹣2a+1=0,
解得a,因此B正确;
∵a+b+c=0,a,
∴b+c=﹣a,即2b+2c=﹣1,因此A正确;
选:ABD.
9.解:如图,连接OC,
∵A为的中点,
∴,
∴AC=AB,
∴∠ACB=∠ABC,
∵∠BAC=120°,
∴∠ACB=∠ABC=30°,
∴∠ADB=∠ACB=30°,
∵BD是直径,
∴∠DAB=90°,
∴∠DBA=60°,
∴∠DBC=∠CBA=30°,
∴,
∴,
∴AD=BC,
A、C正确,
∵∠CAE=∠ACE=30°,
∴CE=AE,
∵∠ABC=30°,
∴BE=2AE=2CE,B错误,
∵∠OCB=∠OBC=∠ACB=∠ABC=30°,
∴四边形OCAB是平行四边形,
∵OC=OB,
∴四边形OCAB是菱形,D正确,
选:ACD.
10.解:令AC,OE交于点F,
由题意得:OE是AC的垂直平分线,
∴EA=EC,
∵AO=OC,
∴△AOE≌△COE,
∴∠AOE=∠COE,
∵OF=OF,AO=AO,
∴△AOF≌△COF,
∴∠OAF=∠OCF,
∵AO∥BC,
∴∠OAF=∠ACE,
∴∠OCA=∠ACE,
∴,选项A正确;
∵∠OCF=∠ECF,∠OFC=∠EFC=90°,CF=CF
∴△EFC≌△OFC,
∴OC=CE=OA,
∵AO∥EC,
四边形AOCE为菱形,选项D正确;
∵,
∴,
∵四边形AOCE为菱形,
∴AE=OC=OD,
∴四边形AEOD为平行四边形,
∴AD=OE,
∴AB=OE,选项B正确;
∠AOD=∠OAE,选项C错误;
选:ABD.
三.填空题(共4小题,满分16分,每小题4分)
11.解:∵设y=﹣6x图象上一点(a,﹣6a),
∴向左平移n个单位,再向上平移2(n+1)个单位,该点坐标为(a﹣n,﹣6a+2n+2),
∵y=﹣6x是“可回旋”函数,
∴﹣6a+2n+2=﹣6(a﹣n),
∴﹣6a+2n+2=﹣6a+6n,
∴4n=2,
∴n,
∴“可回旋单位”是,
答案为:.
12.解:∵每秒旋转45°,则第60秒时,得45°×60=2700°,2700°÷360=7.5周,
∴OD旋转了7周半,
∴此时点D的坐标为(﹣1,﹣1),
答案为:(﹣1,﹣1).
13.解:所有的选购方案:(AD)、(AE)、(BD)、(BE)、(CD)、(CE);
P(A型号饮水机被选中);
答案为:.
14.解:根据前三个正方形的规律可知,左上、左下、右上为相邻的三个偶数,
所以n=10;
最后一个正方形中,左下、右上两数分别为14、16,
所以m=14×16﹣12=212;
所以n+m=222,
答案为:222.
四.解答题(共8小题,满分90分)
15.解:(1)原式=3﹣2+(﹣5)
=3﹣2﹣1
=0;
(2)原式
,
当a=2时,
原式.
16.证明:(1)在矩形ABCD中,AB∥CD,
∴∠B=∠D=90°,
∴∠BAC=∠DCA.
由翻折可知:∠BAE=∠MAEBAC,∠DCF=∠NCFDCA,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF (ASA);
(2)由(1)可知:△ABE≌△CDF,
∴BE=DF,
∵BC=AD,
∴BC﹣BE=AD﹣DF,
∴AF=CE,
∵AF∥CE,
∴四边形ECFA是平行四边形.
17.解:(1)∵反比例函数的图象过点A(﹣1,3),
∴k2=﹣1×3=﹣3,
∴反比例函数的关系式为y;
(2)①作AM⊥x轴于M,BN⊥x轴于N,则AM∥BN,
∴,
∵,AM=3,
∴,
∴BN=1,
∴点B的纵坐标为1,
把y=1代入y得,x=﹣3,
∴B(﹣3,1),
∵一次函数y=k1x+b的图象过点A(﹣1,3)和B(﹣3,1),
∴,
解得k1=1,b=4;
②不等式k1x+b的解集为﹣3<x<﹣1或x>0;
答案为:﹣3<x<﹣1或x>0;
(3)∵S△AOB=S△AOM+S梯形AMNB﹣S△BON=S梯形AMNB(1+3)×(﹣1+3)=4,
∴当F在AB的下方时,F是OA的中点,
∵A(﹣1,3),
∴此时F(,),
当F在AB的上方时,F是点(,)关于A的对称点,
∴此时F(,),
m值为或,
答案为:或.
18.解:(1),
,
;
(2)由表中数据可知,甲、乙平均成绩相等,乙的中位数、众数均大于甲,说明乙的成绩好于甲,虽然乙的方差大于甲,但乙的成绩呈上升趋势,应选乙队员参赛.(答案不唯一,合理即可)
(3)为了夺冠应选乙,因为在10次成绩中,甲只有一次达到9环,而乙有2次达到或超过9环;
为了打破纪录应选乙,因为在10次成绩中,乙有一次达到10环,而甲一次也没有.
19.解:(1)设CD的长为x m,根据题意,
得x(60﹣2x)=450,
即x2﹣30x+225=0,
解得x1=x2=15,
∴EF=DC=15,
∵EF×BF=300,
∴BF=20(m).
答:BF的长是20m.
(2)设CD的长为x m,矩形ABCD的面积为y m2,则,
y=x(60﹣2x)=﹣2(x﹣15)2+450
∴当x=15时,y最大为450m2.
答:当CD的长为15m,矩形ABCD的面积最大,最大为450m2.
20.(1)证明:∵直线CD与⊙O相切于点C,
∴OC⊥CD,
∴∠OCD=90°.
∵OA=OC,
∴∠OAC=∠OCA,
∵DO∥AC,
∴∠COD=∠OCA,∠BOD=∠OAC,
∴∠COD=∠BOD.
在△OCD和△OBD中,
,
∴△OCD≌△OBD(SAS),
∴∠OCD=∠OBD=90°,
∴OB⊥BD,
∵OB是⊙O的半径,
∴BD是⊙O的切线;
(2)解:∵△OCD≌△OBD,
∴CD=BD,
∵OC=OB,
∴OD为BC的垂直平分线,
∴OF⊥BC,BF=FCBC.
∵OB=OE,
∴∠ABE=∠E,
∴tanE=tan∠ABE.
在Rt△BFE中,
∵tanE,
∴,
设BF=k,则EF=2k,CF=k,BC=2k.
∵DO∥AC,CF=BF,
∴OFAC=2,
∴OE=EF﹣OF=2k﹣2,
∴OB=OE=2k﹣2.
∵OF2+BF2=OB2,
∴22+k2=(2k﹣2)2,
解得:k=0(不合题意,舍去)或k.
∴OB,BF,
∴cos∠BOD.
在Rt△OBD中,
∵cos∠BOD,
∴,
∴OD.
21.解:(1)∵抛物线y=ax2﹣4ax+3c交x轴于A,B两点(点A在点B的左边),交y轴正半轴于点C,
令x=0,得y=3c,
∴C(0,3c),
令y=0,得ax2﹣4ax+3c=0,
解得:x1=1,x2=3,
∴A(1,0),B(3,0),
∵OB=OC,
∴3a=3,
解得:a=1,
∴抛物线的解析式为y=x2﹣4x+3;
(2)∵M(m,﹣m﹣3),N(m+2,﹣m﹣5),
∴M,N在直线y=﹣x﹣3上,
MN2,
如图1,过点P作PH⊥直线FK于点E,作PE⊥x轴交直线FK于点E,
设P(t,t2﹣4t+3),则E(t,﹣t﹣3),
∴PE=t2﹣4t+3﹣(﹣t﹣3)=t2﹣3t+6,
∵直线y=﹣x﹣3与x轴交点为F(﹣3,0),与y轴交点为K(0,﹣3),
∴OF=OK=3,
∴∠OKF=45°,
∵PE∥y轴,
∴∠PEH=∠OKF=45°,
∵∠PHE=90°,
∴sin∠PEH=sin45°,
∴PHPE(t2﹣3t+6)(t)2,
∵0,
∴当t时,PH有最小值,此时△PMN的面积最小,
∴S△PMN最小值MN PH2;
(3)∵点P在抛物线上,设P(n,n2﹣4n+3),如图2,
作PE⊥y轴,PG⊥x轴,
设直线AP的解析式为y=k1x+b1(k1≠0),
直线CD的解析式为y=k2x+b2(k2≠0),
将A(1,0),P(n,n2﹣4n+3)代入y=k1x+b1,得,
解得:,
∴直线AP的解析式为y=(n﹣3)x+3﹣n,
∵AP⊥CD,
∴k2,
将C(0,3)代入yx+b2,得:b2=3,
∴直线CD的解析式为yx+3,
联立直线AP,直线CD的解析式,得,
解得:,
∴D(,),
过点D作DK⊥y轴于点K,过点P作PT∥y轴交DK于点T,
∴∠CKD=∠DTP=∠CDP=90°,
∴∠CDK+∠PDT=∠CDK+∠DCK=90°,
∴∠PDT=∠DCK,
∴△PDT∽△DCK,
∴tan∠APC,
∴DT=2CK,
∵CK=3,DT=n,
∴n2[3],
解得:n,
∴点P的横坐标为.
22.解:(1)①点D在⊙C内,连接CD,过点D作CD的垂线,交⊙C于两点A,B,则D是AB的中点,
点E在圆外,点E到⊙C最小的距离为3,大于⊙C的直径2,
点D是⊙C的关联点,点E不是,
答案为:D;
②如图1,
设直线y=﹣x+3与x轴和y轴分别相交于点A,B,则A(3,0),B(0,3),
点A、B到⊙C的最小距离是2,圆的直径是2,
当点P在线段AB时,点P是⊙O的关联点,
∴0≤m≤3;
(3)如图2,
当x=0时,y=2,
∴N(0,2),ON=2,
当y=0时,
0,
∴x=6,
∴M(6,0),OM=6,
∴tan∠NMO,
∴∠NMO=30°,
作CA⊥MN于A,
∴∠CAM=90°,
∴∠ACM=60°,
当AC=3时,点A是⊙C的关联点,
∴AB=AC sin∠ACM=3,
BC=AC cos∠ACM,
当y时,
,
∴x,
∴OB=BC,
∴点C在点O处,c=0,
当M是⊙C的关联点时,MC=3(点C在图中C′点处),c=9,
∴0≤c≤9,
答案为:0≤c≤9.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025年山东淮坊中考数学模拟试题
考试时间:120分钟;总分:150分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共6小题,满分24分,每小题4分)
1.(4分)我国古代数学的发展历史源远流长,曾诞生了很多伟大的数学发现.下列与我国古代数学发现相关的图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.(4分)河南博物院是国家文物局公布的第一批国家一级博物馆,现有馆藏文物17万余件(套),其中国家一级文物与国家二级文物5000多件,历史文化艺术价值极高,一部分藏品被誉为国之重器.这里的数据17万可用科学记数法表示为( )
A.17×104人 B.1.7×105人
C.1.7×106人 D.0.17×106人
3.(4分)一个几何体的三视图都不相同,这个几何体可能是( )
A.四棱锥 B.长、宽、高均不相等的长方体 C.球体 D.圆锥
4.(4分)如图,是甲、乙两家公司的利润增长情况统计图,下列说法正确的是( )
A.甲、乙的利润增长速度一样快 B.甲的利润增长速度比乙快
C.乙的利润增长速度比甲快 D.乙的利润年均增长速度5万元
5.(4分)将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形(△ABC),BC为折痕,若∠1=42°,则∠2的度数为( )
A.48° B.58° C.60° D.69°
6.(4分)若关于x的一元二次方程x2﹣2x+a﹣1=0没有实数根,则a的取值范围是( )
A.a<2 B.a>2 C.a<﹣2 D.a>﹣2
二.多选题(共4小题,满分20分,每小题5分)
(多选)7.(5分)下列命题中正确的是( )
A.121的平方根是±11 B.两个无理数之和一定是无理数
C.实数不是有理数就是无理数 D.带根号的数一定是无理数
(多选)8.(5分)已知抛物线y=ax2+bx+c交x轴于点B(1,0)和点A,交y轴负半轴于点C,且AO=2CO.下列选项正确的是( )
A.2b+2c=﹣1 B.
C. D.4ac+2b+1=0
(多选)9.(5分)如图,△ABC内接于⊙O,BD为⊙O的直径,A为的中点,∠BAC=120°,连接AD、BC交于点E,则下列结论正确的是( )
A.AD=BC B.BE=3CE
C.点A、C为的三等分点 D.连接OC,则四边形ABOC为菱形
(多选)10.(5分)如图,⊙O是△ABC的外接圆,AO∥BC,连接CO并延长交⊙O于点D.分别以点A,C为圆心,以大于的长为半径作弧,并使两弧交于圆外一点M.直线OM交BC于点E,连接AE,下列结论一定正确的是( )
A. B.AB=OE
C.∠AOD=∠BAC D.四边形AOCE为菱形
三.填空题(共4小题,满分16分,每小题4分)
11.(4分)定义:如果函数图象上的一个点向左平移n个单位,再向上平移2(n+1)个单位后仍在这个函数图象上,我们称这个函数是“可回旋”函数,n称为这个函数的“可回旋单位”.如果y=﹣6x是“可回旋”函数,那么这个函数的“可回旋单位”是 .
12.(4分)如图,已知OD为等边△OAC的高,顶点O(0,0),D(1,1),若△OAC绕点O逆时针旋转,每秒旋转45°,则第60秒时,D点坐标为 .
13.(4分)某超市有A,B,C三种型号的甲种品牌饮水机和D,E两种型号的乙种品牌饮水机,某中学准备从甲、乙两种品牌的饮水机中各选购一种型号的饮水机安装到教室.如果各种选购方案被选中的可能性相同,那么A型号饮水机被选中的概率是 .
14.(4分)图中各正方形中的四个数之间都有相同的规律,则根据这种规律,第四个正方形中的n与最后一个正方形中的m之和,n+m= .
四.解答题(共8小题,满分90分)
15.(10分)(1)计算:()﹣1+(﹣5)×||;
(2)先化简,再求值:(1),其中a=2.
16.(10分)如图,在矩形ABCD中,M,N是对角线AC上的两点,将矩形折叠分别使点B与点M重合,点D与点N重合,折痕分别为AE,CF.连接EF,交AC于点O.
(1)求证:△ABE≌△CDF.
(2)求证:四边形ECFA是平行四边形.
17.(10分)如图,在平面直角坐标系中,一次函数y=k1x+b的图象与反比例函数的图象的两个交点为A(﹣1,3)和B.
(1)求反比例函数的关系式;
(2)若一次函数y=k1x+b与x轴交于点C,且;
①求出k1与b的值;
②直接写出不等式k1x+b的解集为 ;
(3)在(2)的基础上,若点F是直线OA上一点,F点的横坐标为m,连接AF,BF,△ABF的面积记为S,当S=2时,请直接写出m值 .
18.(11分)甲、乙两名队员参加射击训练(各射击10次),成绩分别被制成下列两个统计图(如图).
根据以上信息,整理分析数据如表:
(1)求出表格中a,b,c的值;
平均成绩/环 中位数/环 众数/环 方差
甲 a 7 7 1.2
乙 7 b 8 c
(2)请你运用表中的统计量,分别分析这两名队员的射击成绩;
(3)记录表明,成绩达到9环就很可能夺冠,你认为为了夺冠应选谁参加这项比赛?说明理由;如果成绩达到10环就可能打破纪录,那么你认为为了打破纪录应选谁参加这项比赛呢?说明理由.
19.(10分)如图,某工地在直角墙角处,用可建60米长围墙的建筑材料围成一个矩形堆物场地,中间用同样的材料分隔为两间.
(1)若所围成的矩形ABFE和矩形CDEF的面积分别是300m2和150m2,求BF的长.
(2)当CD的长为多少时,所围成的矩形ABCD的面积最大?并求出最大面积.
20.(12分)如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,直线CD与⊙O相切于点C,DO∥AC交弦BC于点F,交优弧于点E,连接BD,BE.
(1)求证:BD是⊙O的切线;
(2)若,AC=4,求OD的长.
21.(14分)如图,抛物线y=ax2﹣4ax+3a交x轴于A,B两点(点A在点B的左边),交y轴正半轴于点C,OB=OC,点P在抛物线上.
(1)求抛物线的解析式;
(2)平面上有两点M(m,﹣m﹣3),N(m+2,﹣m﹣5),求△PMN的面积的最小值;
(3)若tan∠APC,求点P的横坐标.
22.(13分)在平面直角坐标系xOy中,对于点P和半径为1的⊙C给出如下定义:若过点P的直线l交⊙C于A,B两点,在P,A,B三点中,其中一点恰为以另外两点为端点的线段中点时,则称点P为⊙C的关联点.
(1)当点C与O重合时,
①在点,E(4,0)中,⊙C的关联点是 ;
②已知点P(m,n)在直线y=﹣x+3上,若点P为⊙C的关联点,求m的取值范围;
(2)⊙C的圆心C(c,0),直线与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的关联点P,则c的取值范围是 .
参考答案
一.选择题(共6小题,满分24分,每小题4分)
1.解:A.是轴对称图形,不是中心对称图形,不符合题意.
B.既是轴对称图形,又是中心对称图形,符合题意.
C.是中心对称图形,不是轴对称图形,不符合题意.
D.既不是轴对称图形,也不是中心对称图形,不符合题意.
选:B.
2.解:17万=1.7×105,
选:B.
3.解:A,四棱锥的左视图和主视图都是三角形,不合题意;
B,长、宽、高均不相等的长方体的三视图都是长方形,但长、宽不同,符合题意;
C,球体的三视图都是圆形,不合题意;
D,圆锥的左视图和主视图都是三角形,不合题意;
选:B.
4.解:由图知,甲利润6年时间从50万增加到70万,而乙利润3年时间从50万增加到70万,
所以乙的利润增长速度比甲快,
选:C.
5.解:如图所示,
∵长方形的两条长边平行,∠1=42°,
∴∠1=∠4=42°,∠4=∠5,
∴∠5=42°,
由折叠的性质可知,∠2=∠3,
∵∠2+∠3+∠5=180°,
∴∠2=69°,
选:D.
6.解:由题意可知:Δ=4﹣4(a﹣1)<0,
∴a>2,
选:B.
二.多选题(共4小题,满分20分,每小题5分)
7.解:A.121的平方根是±11,正确,符合题意;
B.两个无理数之和不一定是无理数,错误,不符合题意;
C.实数不是有理数就是无理数,正确,符合题意;
D.带根号的数不一定是无理数,错误,不符合题意.
选:AC.
8.解:由抛物线的位置可知,a>0,b>0,c<0,因此<0,C不正确;
抛物线y=ax2+bx+c过点B (1,0),因此有a+b+c=0,
抛物线与y轴的交点C(0,c),
∵OA=2OC,
∴点A(2c,0),代入抛物线关系式得,4ac2+2bc+c=0,即4ac+2b+1=0,因此D正确;
∵点A(2c,0),B(1,0),
∴对称轴x,即4ac+2a+2b=0,
所以﹣2a+1=0,
解得a,因此B正确;
∵a+b+c=0,a,
∴b+c=﹣a,即2b+2c=﹣1,因此A正确;
选:ABD.
9.解:如图,连接OC,
∵A为的中点,
∴,
∴AC=AB,
∴∠ACB=∠ABC,
∵∠BAC=120°,
∴∠ACB=∠ABC=30°,
∴∠ADB=∠ACB=30°,
∵BD是直径,
∴∠DAB=90°,
∴∠DBA=60°,
∴∠DBC=∠CBA=30°,
∴,
∴,
∴AD=BC,
A、C正确,
∵∠CAE=∠ACE=30°,
∴CE=AE,
∵∠ABC=30°,
∴BE=2AE=2CE,B错误,
∵∠OCB=∠OBC=∠ACB=∠ABC=30°,
∴四边形OCAB是平行四边形,
∵OC=OB,
∴四边形OCAB是菱形,D正确,
选:ACD.
10.解:令AC,OE交于点F,
由题意得:OE是AC的垂直平分线,
∴EA=EC,
∵AO=OC,
∴△AOE≌△COE,
∴∠AOE=∠COE,
∵OF=OF,AO=AO,
∴△AOF≌△COF,
∴∠OAF=∠OCF,
∵AO∥BC,
∴∠OAF=∠ACE,
∴∠OCA=∠ACE,
∴,选项A正确;
∵∠OCF=∠ECF,∠OFC=∠EFC=90°,CF=CF
∴△EFC≌△OFC,
∴OC=CE=OA,
∵AO∥EC,
四边形AOCE为菱形,选项D正确;
∵,
∴,
∵四边形AOCE为菱形,
∴AE=OC=OD,
∴四边形AEOD为平行四边形,
∴AD=OE,
∴AB=OE,选项B正确;
∠AOD=∠OAE,选项C错误;
选:ABD.
三.填空题(共4小题,满分16分,每小题4分)
11.解:∵设y=﹣6x图象上一点(a,﹣6a),
∴向左平移n个单位,再向上平移2(n+1)个单位,该点坐标为(a﹣n,﹣6a+2n+2),
∵y=﹣6x是“可回旋”函数,
∴﹣6a+2n+2=﹣6(a﹣n),
∴﹣6a+2n+2=﹣6a+6n,
∴4n=2,
∴n,
∴“可回旋单位”是,
答案为:.
12.解:∵每秒旋转45°,则第60秒时,得45°×60=2700°,2700°÷360=7.5周,
∴OD旋转了7周半,
∴此时点D的坐标为(﹣1,﹣1),
答案为:(﹣1,﹣1).
13.解:所有的选购方案:(AD)、(AE)、(BD)、(BE)、(CD)、(CE);
P(A型号饮水机被选中);
答案为:.
14.解:根据前三个正方形的规律可知,左上、左下、右上为相邻的三个偶数,
所以n=10;
最后一个正方形中,左下、右上两数分别为14、16,
所以m=14×16﹣12=212;
所以n+m=222,
答案为:222.
四.解答题(共8小题,满分90分)
15.解:(1)原式=3﹣2+(﹣5)
=3﹣2﹣1
=0;
(2)原式
,
当a=2时,
原式.
16.证明:(1)在矩形ABCD中,AB∥CD,
∴∠B=∠D=90°,
∴∠BAC=∠DCA.
由翻折可知:∠BAE=∠MAEBAC,∠DCF=∠NCFDCA,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF (ASA);
(2)由(1)可知:△ABE≌△CDF,
∴BE=DF,
∵BC=AD,
∴BC﹣BE=AD﹣DF,
∴AF=CE,
∵AF∥CE,
∴四边形ECFA是平行四边形.
17.解:(1)∵反比例函数的图象过点A(﹣1,3),
∴k2=﹣1×3=﹣3,
∴反比例函数的关系式为y;
(2)①作AM⊥x轴于M,BN⊥x轴于N,则AM∥BN,
∴,
∵,AM=3,
∴,
∴BN=1,
∴点B的纵坐标为1,
把y=1代入y得,x=﹣3,
∴B(﹣3,1),
∵一次函数y=k1x+b的图象过点A(﹣1,3)和B(﹣3,1),
∴,
解得k1=1,b=4;
②不等式k1x+b的解集为﹣3<x<﹣1或x>0;
答案为:﹣3<x<﹣1或x>0;
(3)∵S△AOB=S△AOM+S梯形AMNB﹣S△BON=S梯形AMNB(1+3)×(﹣1+3)=4,
∴当F在AB的下方时,F是OA的中点,
∵A(﹣1,3),
∴此时F(,),
当F在AB的上方时,F是点(,)关于A的对称点,
∴此时F(,),
m值为或,
答案为:或.
18.解:(1),
,
;
(2)由表中数据可知,甲、乙平均成绩相等,乙的中位数、众数均大于甲,说明乙的成绩好于甲,虽然乙的方差大于甲,但乙的成绩呈上升趋势,应选乙队员参赛.(答案不唯一,合理即可)
(3)为了夺冠应选乙,因为在10次成绩中,甲只有一次达到9环,而乙有2次达到或超过9环;
为了打破纪录应选乙,因为在10次成绩中,乙有一次达到10环,而甲一次也没有.
19.解:(1)设CD的长为x m,根据题意,
得x(60﹣2x)=450,
即x2﹣30x+225=0,
解得x1=x2=15,
∴EF=DC=15,
∵EF×BF=300,
∴BF=20(m).
答:BF的长是20m.
(2)设CD的长为x m,矩形ABCD的面积为y m2,则,
y=x(60﹣2x)=﹣2(x﹣15)2+450
∴当x=15时,y最大为450m2.
答:当CD的长为15m,矩形ABCD的面积最大,最大为450m2.
20.(1)证明:∵直线CD与⊙O相切于点C,
∴OC⊥CD,
∴∠OCD=90°.
∵OA=OC,
∴∠OAC=∠OCA,
∵DO∥AC,
∴∠COD=∠OCA,∠BOD=∠OAC,
∴∠COD=∠BOD.
在△OCD和△OBD中,
,
∴△OCD≌△OBD(SAS),
∴∠OCD=∠OBD=90°,
∴OB⊥BD,
∵OB是⊙O的半径,
∴BD是⊙O的切线;
(2)解:∵△OCD≌△OBD,
∴CD=BD,
∵OC=OB,
∴OD为BC的垂直平分线,
∴OF⊥BC,BF=FCBC.
∵OB=OE,
∴∠ABE=∠E,
∴tanE=tan∠ABE.
在Rt△BFE中,
∵tanE,
∴,
设BF=k,则EF=2k,CF=k,BC=2k.
∵DO∥AC,CF=BF,
∴OFAC=2,
∴OE=EF﹣OF=2k﹣2,
∴OB=OE=2k﹣2.
∵OF2+BF2=OB2,
∴22+k2=(2k﹣2)2,
解得:k=0(不合题意,舍去)或k.
∴OB,BF,
∴cos∠BOD.
在Rt△OBD中,
∵cos∠BOD,
∴,
∴OD.
21.解:(1)∵抛物线y=ax2﹣4ax+3c交x轴于A,B两点(点A在点B的左边),交y轴正半轴于点C,
令x=0,得y=3c,
∴C(0,3c),
令y=0,得ax2﹣4ax+3c=0,
解得:x1=1,x2=3,
∴A(1,0),B(3,0),
∵OB=OC,
∴3a=3,
解得:a=1,
∴抛物线的解析式为y=x2﹣4x+3;
(2)∵M(m,﹣m﹣3),N(m+2,﹣m﹣5),
∴M,N在直线y=﹣x﹣3上,
MN2,
如图1,过点P作PH⊥直线FK于点E,作PE⊥x轴交直线FK于点E,
设P(t,t2﹣4t+3),则E(t,﹣t﹣3),
∴PE=t2﹣4t+3﹣(﹣t﹣3)=t2﹣3t+6,
∵直线y=﹣x﹣3与x轴交点为F(﹣3,0),与y轴交点为K(0,﹣3),
∴OF=OK=3,
∴∠OKF=45°,
∵PE∥y轴,
∴∠PEH=∠OKF=45°,
∵∠PHE=90°,
∴sin∠PEH=sin45°,
∴PHPE(t2﹣3t+6)(t)2,
∵0,
∴当t时,PH有最小值,此时△PMN的面积最小,
∴S△PMN最小值MN PH2;
(3)∵点P在抛物线上,设P(n,n2﹣4n+3),如图2,
作PE⊥y轴,PG⊥x轴,
设直线AP的解析式为y=k1x+b1(k1≠0),
直线CD的解析式为y=k2x+b2(k2≠0),
将A(1,0),P(n,n2﹣4n+3)代入y=k1x+b1,得,
解得:,
∴直线AP的解析式为y=(n﹣3)x+3﹣n,
∵AP⊥CD,
∴k2,
将C(0,3)代入yx+b2,得:b2=3,
∴直线CD的解析式为yx+3,
联立直线AP,直线CD的解析式,得,
解得:,
∴D(,),
过点D作DK⊥y轴于点K,过点P作PT∥y轴交DK于点T,
∴∠CKD=∠DTP=∠CDP=90°,
∴∠CDK+∠PDT=∠CDK+∠DCK=90°,
∴∠PDT=∠DCK,
∴△PDT∽△DCK,
∴tan∠APC,
∴DT=2CK,
∵CK=3,DT=n,
∴n2[3],
解得:n,
∴点P的横坐标为.
22.解:(1)①点D在⊙C内,连接CD,过点D作CD的垂线,交⊙C于两点A,B,则D是AB的中点,
点E在圆外,点E到⊙C最小的距离为3,大于⊙C的直径2,
点D是⊙C的关联点,点E不是,
答案为:D;
②如图1,
设直线y=﹣x+3与x轴和y轴分别相交于点A,B,则A(3,0),B(0,3),
点A、B到⊙C的最小距离是2,圆的直径是2,
当点P在线段AB时,点P是⊙O的关联点,
∴0≤m≤3;
(3)如图2,
当x=0时,y=2,
∴N(0,2),ON=2,
当y=0时,
0,
∴x=6,
∴M(6,0),OM=6,
∴tan∠NMO,
∴∠NMO=30°,
作CA⊥MN于A,
∴∠CAM=90°,
∴∠ACM=60°,
当AC=3时,点A是⊙C的关联点,
∴AB=AC sin∠ACM=3,
BC=AC cos∠ACM,
当y时,
,
∴x,
∴OB=BC,
∴点C在点O处,c=0,
当M是⊙C的关联点时,MC=3(点C在图中C′点处),c=9,
∴0≤c≤9,
答案为:0≤c≤9.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
