广东省东山中学09-10学年高二上学期期中考试(数学文)
文档属性
| 名称 | 广东省东山中学09-10学年高二上学期期中考试(数学文) |  | |
| 格式 | rar | ||
| 文件大小 | 179.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-11-26 20:53:00 | ||
图片预览



文档简介
广东梅县东山中学09-10学年高二上学期期中考试
数学文科 2009-11
命题人:曾巧志、徐世琴 校对人:丘艳平、丘利华
一、选择题(本题共10题,每题5分,共50分)
1.要从165人中抽取15人进行身体健康检查,现采用分层抽样法进行抽取,若这165人中,老年人的人数为22人,则老年人中被抽取到参加健康检查的人数是( )
.5 .2 .3 .1
2.在中,三内角的对边分别是,若,则角为( )
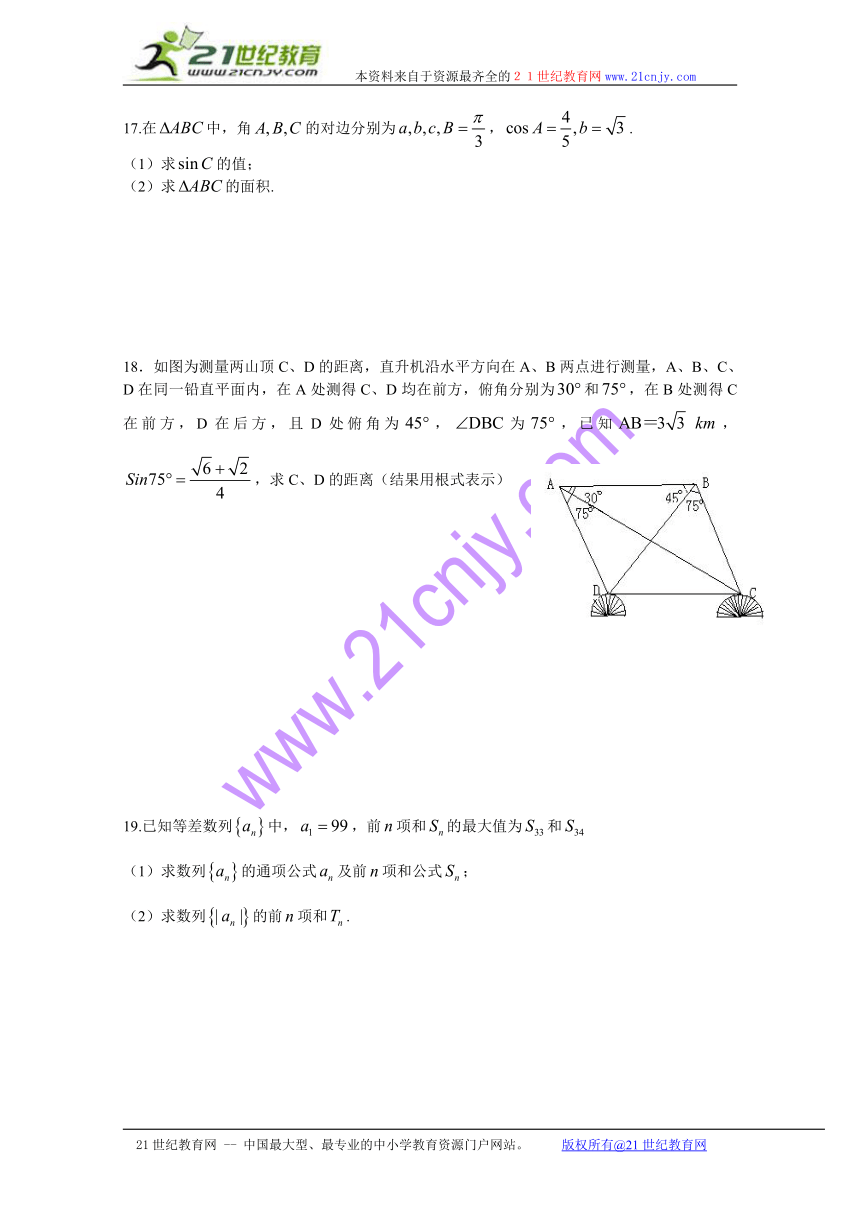
. .或 . .或
3.在中,若,则角等于( )
. . . .
4.边长为的三角形的最大角与最小角之和是( )
. . . .
5.已知为钝角三角形,角A、B、C所对的边是,,角为钝角,则的取值范围为( )
. . . .
6.某工厂对一批产品进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
. . . .
7.等差数列的前n项和分别为,已知,则为( )
.7 . . .
8.设等差数列的前n项和是Sn,若,则( )
. . . .
9.设等差数列的前前n项和是,若为一个确定的常数,则下面各数中也为确定的常数的是( )
. . . .
10.已知是等比数列,,则( )
. . . .
二、填空题(本题共4题,每题5分,共20分)
11.在中,已知,则=__________.
12.设有一个正方形网格,其中每个正方形的边长都等于6cm,现用直径等于2cm的硬币投掷到此网格上,则硬币落下后与格线有公共点的概率_______.
13.已知公差不为0的等差数列的第2,3,6项依次构成等比数列,则该等比数列的公比是________.
14.数列满足,若,则________.
三、解答题(本题共6题,其中第16~17每题12分,第15、18~20每题14分,共80分)
15.某校高二年级有学生1000人,在某次数学考试中,为研究学生的考试情况,需从中抽取40名学生的成绩,
(1)问采用何种抽样方法更合适?
(2)根据所抽取的40名学生成绩,分组在,,的频率分布直方图中对应的小矩形的高分别是,问所取的40名学生的成绩不低于分的共有多少人?
(3)在(2)所求的成绩不低于分的学生中任取2人为一组(不分先后),求至少有1人的成绩在内的概率.
16.求数列的前n项和.
17.在中,角的对边分别为,.
(1)求的值;
(2)求的面积.
18.如图为测量两山顶C、D的距离,直升机沿水平方向在A、B两点进行测量,A、B、C、D在同一铅直平面内,在A处测得C、D均在前方,俯角分别为和,在B处测得C在前方,D在后方,且D处俯角为,为,已知,,求C、D的距离(结果用根式表示)
19.已知等差数列中,,前项和的最大值为和
(1)求数列的通项公式及前项和公式;
(2)求数列的前项和.
20.在数列中,
(1)求证:数列是等比数列,并求出数列的通项公式.
(2)令,求数列的前项和.
(3)求数列的前n项和.
广东梅县东山中学高二文科数学中段考试题答案
一、选择题(本题共10题,每题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
B
B
A
B
B
C
C
二、填空题(本题共4题,每题5分,共20分)
11、 12、 13、3 14、
三、解答题(本题共6题,其中16、17每题12分,15、18、19、20每题14分,共80分)
15.解:(1)系统抽样方法更合适..................................2分
(2)由题意得:
在分组,,中的学生频率分别是
, , ............................................4分
所以所取的40名学生的成绩不低于120分的人数为:
人 ....................................................6分
(3)由(2)知成绩在的学生有4人,设编号为1、2、3、4
成绩在的学生有2人,设编号为5、6
成绩在的学生有2人,设编号为7、8 ...........................................7分
则从这8人中任取2人为一组共有的分组方法为:
(1、2)、(1、3)、(1、4)、(1、5)、(1、6)、(1、7)、(1、8)
(2、3)、(2、4)、(2、5)、(2、6)、(2、7)、(2、8)
(3、4)、(3、5)、(3、6)、(3、7)、(3、8)
(4、5)、(4、6)、(4、7)、(4、8)
(5、6)、(5、7)、(5、8)
(6、7)、(6、8)
(7、8)
共28种分组方法,且是等可能基本事件 ..............................................10分
记事件A为“至少有1人的成绩在内”...................................................11分
则事件为“2人的成绩均在内”
因为事件所包含的基本事件有6个,所以:.............................................12分
= = ...................................................13分
答:(1)系统抽样
(2)所取40名学生成绩不低于120分的有8人
(3)至少有1人的成绩在内的概率为...........................................14分
16.解: ......................................2分
.............................................6分
= ......................................................................12分
17.解:(1)因为是的内角
,
.................................................................2分
则............................................4分
........................................................................6分
(2)由(I)知,
又因为,
在中,由正弦定理得:
......................................................9分
则................................................................10分
....................................................12分
18.解:如图所示:在中:
因为,
.....................................2分
又在中:因为
由正弦定理得:
...............................................4分
............................................................6分
又因为 ..................................................8分
在中,由余弦定理得:
............................................................10分
...............................................................13分
答:C、D 的距离为。 ......................................................................14分
19.解:(1)设的公差为,由题意得:
………………………………….2分
解得……………………………………………………4分
……………………………5分
…7分
(2)令
得
则 当时,;
当时,……………………………………….8分
①当时
…………………………10
②当时
……………………………………….13分
综上所述………………………14分
20.解:(1)由已知得 且
故数列是以为首项,为公比的等比数列
从而
所以 .................................................................3分
(2)由得
两式相减得:
得 ....................................................9分
(3)由
得
即:
= ........................................14分
数学文科 2009-11
命题人:曾巧志、徐世琴 校对人:丘艳平、丘利华
一、选择题(本题共10题,每题5分,共50分)
1.要从165人中抽取15人进行身体健康检查,现采用分层抽样法进行抽取,若这165人中,老年人的人数为22人,则老年人中被抽取到参加健康检查的人数是( )
.5 .2 .3 .1
2.在中,三内角的对边分别是,若,则角为( )
. .或 . .或
3.在中,若,则角等于( )
. . . .
4.边长为的三角形的最大角与最小角之和是( )
. . . .
5.已知为钝角三角形,角A、B、C所对的边是,,角为钝角,则的取值范围为( )
. . . .
6.某工厂对一批产品进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
. . . .
7.等差数列的前n项和分别为,已知,则为( )
.7 . . .
8.设等差数列的前n项和是Sn,若,则( )
. . . .
9.设等差数列的前前n项和是,若为一个确定的常数,则下面各数中也为确定的常数的是( )
. . . .
10.已知是等比数列,,则( )
. . . .
二、填空题(本题共4题,每题5分,共20分)
11.在中,已知,则=__________.
12.设有一个正方形网格,其中每个正方形的边长都等于6cm,现用直径等于2cm的硬币投掷到此网格上,则硬币落下后与格线有公共点的概率_______.
13.已知公差不为0的等差数列的第2,3,6项依次构成等比数列,则该等比数列的公比是________.
14.数列满足,若,则________.
三、解答题(本题共6题,其中第16~17每题12分,第15、18~20每题14分,共80分)
15.某校高二年级有学生1000人,在某次数学考试中,为研究学生的考试情况,需从中抽取40名学生的成绩,
(1)问采用何种抽样方法更合适?
(2)根据所抽取的40名学生成绩,分组在,,的频率分布直方图中对应的小矩形的高分别是,问所取的40名学生的成绩不低于分的共有多少人?
(3)在(2)所求的成绩不低于分的学生中任取2人为一组(不分先后),求至少有1人的成绩在内的概率.
16.求数列的前n项和.
17.在中,角的对边分别为,.
(1)求的值;
(2)求的面积.
18.如图为测量两山顶C、D的距离,直升机沿水平方向在A、B两点进行测量,A、B、C、D在同一铅直平面内,在A处测得C、D均在前方,俯角分别为和,在B处测得C在前方,D在后方,且D处俯角为,为,已知,,求C、D的距离(结果用根式表示)
19.已知等差数列中,,前项和的最大值为和
(1)求数列的通项公式及前项和公式;
(2)求数列的前项和.
20.在数列中,
(1)求证:数列是等比数列,并求出数列的通项公式.
(2)令,求数列的前项和.
(3)求数列的前n项和.
广东梅县东山中学高二文科数学中段考试题答案
一、选择题(本题共10题,每题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
B
B
A
B
B
C
C
二、填空题(本题共4题,每题5分,共20分)
11、 12、 13、3 14、
三、解答题(本题共6题,其中16、17每题12分,15、18、19、20每题14分,共80分)
15.解:(1)系统抽样方法更合适..................................2分
(2)由题意得:
在分组,,中的学生频率分别是
, , ............................................4分
所以所取的40名学生的成绩不低于120分的人数为:
人 ....................................................6分
(3)由(2)知成绩在的学生有4人,设编号为1、2、3、4
成绩在的学生有2人,设编号为5、6
成绩在的学生有2人,设编号为7、8 ...........................................7分
则从这8人中任取2人为一组共有的分组方法为:
(1、2)、(1、3)、(1、4)、(1、5)、(1、6)、(1、7)、(1、8)
(2、3)、(2、4)、(2、5)、(2、6)、(2、7)、(2、8)
(3、4)、(3、5)、(3、6)、(3、7)、(3、8)
(4、5)、(4、6)、(4、7)、(4、8)
(5、6)、(5、7)、(5、8)
(6、7)、(6、8)
(7、8)
共28种分组方法,且是等可能基本事件 ..............................................10分
记事件A为“至少有1人的成绩在内”...................................................11分
则事件为“2人的成绩均在内”
因为事件所包含的基本事件有6个,所以:.............................................12分
= = ...................................................13分
答:(1)系统抽样
(2)所取40名学生成绩不低于120分的有8人
(3)至少有1人的成绩在内的概率为...........................................14分
16.解: ......................................2分
.............................................6分
= ......................................................................12分
17.解:(1)因为是的内角
,
.................................................................2分
则............................................4分
........................................................................6分
(2)由(I)知,
又因为,
在中,由正弦定理得:
......................................................9分
则................................................................10分
....................................................12分
18.解:如图所示:在中:
因为,
.....................................2分
又在中:因为
由正弦定理得:
...............................................4分
............................................................6分
又因为 ..................................................8分
在中,由余弦定理得:
............................................................10分
...............................................................13分
答:C、D 的距离为。 ......................................................................14分
19.解:(1)设的公差为,由题意得:
………………………………….2分
解得……………………………………………………4分
……………………………5分
…7分
(2)令
得
则 当时,;
当时,……………………………………….8分
①当时
…………………………10
②当时
……………………………………….13分
综上所述………………………14分
20.解:(1)由已知得 且
故数列是以为首项,为公比的等比数列
从而
所以 .................................................................3分
(2)由得
两式相减得:
得 ....................................................9分
(3)由
得
即:
= ........................................14分
同课章节目录
