2024-2025学年甘肃省武威第二十中学中考数学《二次根式》基础知识点专项训练(含答案)
文档属性
| 名称 | 2024-2025学年甘肃省武威第二十中学中考数学《二次根式》基础知识点专项训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 864.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-07 20:56:12 | ||
图片预览



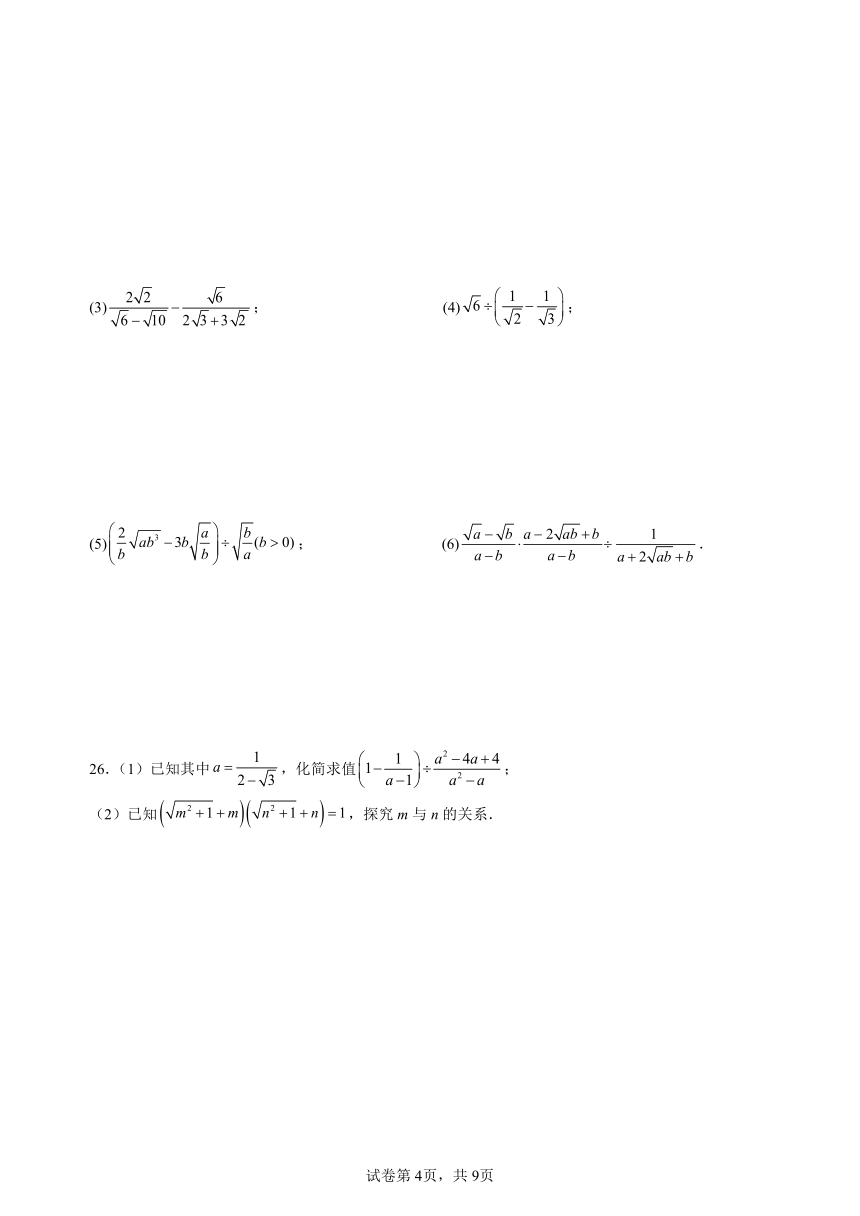

文档简介
2024-2025学年甘肃省武威第二十中学中考数学《二次根式》
基础知识点专项训练
一、单选题
1.化简的结果是( )
A. B. C.2 D.
2.已知,则整数的值为( )
A. B. C. D.
3.已知,则的值为( )
A.0 B.1 C. D.
4.设,的最小值为,使得取最小值的x值为n,则( )
A.8 B.6 C. D.
5.估计的值在数轴上最可能表示的点是( )
A. B. C. D.
6.实数在数轴上的位置如图所示,则化简后为( )
A.7 B. C. D.无法确定
7.已知,化简的结果为( )
A.1 B. C. D.
8.已知,则代数式的值为( )
A. B. C. D.
9.若,,则a与b的大小关系是( )
A.a>b B.a10.已知.则xy=( )
A.8 B.9 C.10 D.11
11.设a为的小数部分,b为的小数部分,则的值为( )
A. B. C. D.
12.已知多项式,下列说法正确的有( )个:
①若,则;
②若为整数,则整数的值为2或6;
③的最小值为;
④令,则.
A.1 B.2 C.3 D.4
13.如图是一个按某种规律排列的数阵:
根据数阵排列的规律,第n(n是整数,且n≥4)行从左向右数第(n-3)个数是(用含n的代数式表示)( ).
A. B. C. D.
14.二次根式除法可以这样解:如.像这样通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫分母有理化,判断下列选项正确的是( )
①若a是的小数部分,则的值为1;
②比较两个二次根式的大小;
③计算;
④对于式子,对它的分子分母同时乘以或或,均不能对其分母有理化;
⑤设实数x,y满足,则;
⑥若,,且,则正整数.
A.①④⑤ B.②③④ C.②④⑤⑥ D.②④⑥
二、填空题
15.化简: .
16.设,则 .
17.设正整数a、m、n满足.则 .
18.设,则的值为 .
19.当时,多项式的值为
20.已知,则的算术平方根是 .
21.有如下一串二次根式:;;;,仿照,写出第个二次根式 .
22.已知m为正整数,若是整数,则根据可知m有最小值.设n为正整数,若是大于1的整数,则n的最小值为 ,最大值为 ,的小数部分为 .
23.已知,则的值为 .
24.设,,当t为 时,代数式.
三、解答题
25.计算
(1); (2);
(3); (4);
(5); (6).
26.(1)已知其中,化简求值;
(2)已知,探究m与n的关系.
27.先化简,再求值
(1),其中,;
(2),其中,.
28.(1)计算:;
(2)已知a、b、c满足.判断以a、b、c为边能否构成三角形?若能构成三角形,说明此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
29.阅读下列材料,然后回答问题.
①在进行二次根式的化简与运算时,我们有时会碰上如一样的式子,可以将其进一步化简:
以上这种化简的步骤叫做分母有理化.
②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算.
(1)计算:.
(2)已知m是正整数,,,,求m.
(3)已知,则的值为
30.【阅读材料】
像,,,两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.
例如,与,与,与 ,等都是互为有理化因式.进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
(1)的有理化因式为 ;
(2)化简:;
(3)①如图,中,与的角平分线相交于点P,若的周长为,面积为3,则点P到边的距离为 .
②已知有理数a、b满足,求a、b的值.
31.先阅读,后解答:
;
像上述解题过程中,与,与相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程中也称为分母有理化
(1)的有理化因式为________;的有理化因式为________.
(2)化简:.
(3)计算:
32.阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如,善于思考的小明进行了以下探索:
若设(其中a、b、m、n均为整数),则有.这样小明就找到了一种把类似的式子化为平方式的方法,请你仿照小明的方法探索并解决下列问题:
(1)若,当a、b、m、n均为整数时,用含m、n的式子分别表示a、b,得:a= ,b= ;
(2)若,且a、m、n均为正整数,求a的值;
(3)化简:.
33.阅读材料:像;;…两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如与,与,与等都是互为有理化因式.在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.例如:;.解答下列问题:
(1)与______互为有理化因式,将分母有理化得______;
(2)①比较大小:______(填,,,或中的一种)
②计算下列式子的值:
③已知正整数a、b满足,求a,b的值.
34.材料一:有这样一类题目:将化简,如果你能找到两个数m、n,使m2+n2=a且mm=,则将a±2将变成m2+n2±2n,即变成(m±n)2开方,从而使得化简.
例如,5±2=3+2±2=()2+()2±2×=( ±)2,所以== ±:
材料二:在进行二次根式的化简时,我们有时会碰到如,,.这样的式子==(一);==(二);===﹣1(三)以上这种化简的步骤叫做分母有理化.
还可以用以下方法化简:====﹣1(四);
请根据材料解答下列问题:
(1)= ;= .
(2)化简: ++…+.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1-14 DBCDD AACBD BBCC
15.
16.
17.3
18.
19.
20.
21.
22. 3 75
23./
24.2
25.(1)解:原式
;
(2)解:原式
.
(3)解:原式
;
(4)解:原式
;
(5)解:原式
;
(6)解:原式
.
26.解:(1)
,
,
原式;
(2)
,
,即,
,
,即,
.
27.(1)原式
当,时,
原式
(2)原式
当,时,
原式
28.解:(1)
=
=
=4;
(2)以a、b、c为边能构成三角形,此三角形的形状是直角三角形,
理由是:
∵a、b、c满足,
∴a﹣2=0,3﹣b=0,c﹣=0,
∴a=2,b=3,c=,
∵2+3>,2+>3,2+>3,
∴以a、b、c为边能组成三角形,
∵a=2,b=3,c=,
∴a2+b2=c2,
∴以a、b、c为边能构成直角三角形,直角边是a和b,
则此三角形的面积是=3.
29.(1)解:
;
(2),,
,,,
,
,
,
;
(3)设,,则,
,
,
,
,
,
,
.(舍去),
.
30.(1)解:根据题意可知:,
∴的有理化因式为;
故答案为:.
(2)
;
(3)①过点分别作边、、的垂线段、、,
中,与的角平分线相交于点,
线段,
,
的周长为,面积为3,
,
解得,
即点P到边的距离为;
②
∴,解得:.
31.(1)解:,,
∴的有理化因式是,的有理化因式是,
故答案为:;;
(2)解:
;
(3)解:(n为正整数)
,
∴
.
32.(1)∵,
∴,
∴.
故答案为:,;
(2)∵,
∴,6=2mn,
∴mn=3.
∵a、m、n均为正整数,
∴m=1,n=3或m=3,n=1.
当m=1,n=3时,;
当m=3,n=1时,.
∴a的值为28或12;
(3)令,
则
∴.
33.(1)解:与互为有理化因式,
,
故答案为:,;
(2)解:①,,
,,
,
,
,
故答案为:;
②
,
;
③
,
,
,
,
,,
.
34.(1)解:∵,
,
∴=,
,
故答案为:,;
(2)解:∵===﹣1,
,
,
,
∴原式=
=.
答案第1页,共2页
答案第1页,共2页
基础知识点专项训练
一、单选题
1.化简的结果是( )
A. B. C.2 D.
2.已知,则整数的值为( )
A. B. C. D.
3.已知,则的值为( )
A.0 B.1 C. D.
4.设,的最小值为,使得取最小值的x值为n,则( )
A.8 B.6 C. D.
5.估计的值在数轴上最可能表示的点是( )
A. B. C. D.
6.实数在数轴上的位置如图所示,则化简后为( )
A.7 B. C. D.无法确定
7.已知,化简的结果为( )
A.1 B. C. D.
8.已知,则代数式的值为( )
A. B. C. D.
9.若,,则a与b的大小关系是( )
A.a>b B.a10.已知.则xy=( )
A.8 B.9 C.10 D.11
11.设a为的小数部分,b为的小数部分,则的值为( )
A. B. C. D.
12.已知多项式,下列说法正确的有( )个:
①若,则;
②若为整数,则整数的值为2或6;
③的最小值为;
④令,则.
A.1 B.2 C.3 D.4
13.如图是一个按某种规律排列的数阵:
根据数阵排列的规律,第n(n是整数,且n≥4)行从左向右数第(n-3)个数是(用含n的代数式表示)( ).
A. B. C. D.
14.二次根式除法可以这样解:如.像这样通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫分母有理化,判断下列选项正确的是( )
①若a是的小数部分,则的值为1;
②比较两个二次根式的大小;
③计算;
④对于式子,对它的分子分母同时乘以或或,均不能对其分母有理化;
⑤设实数x,y满足,则;
⑥若,,且,则正整数.
A.①④⑤ B.②③④ C.②④⑤⑥ D.②④⑥
二、填空题
15.化简: .
16.设,则 .
17.设正整数a、m、n满足.则 .
18.设,则的值为 .
19.当时,多项式的值为
20.已知,则的算术平方根是 .
21.有如下一串二次根式:;;;,仿照,写出第个二次根式 .
22.已知m为正整数,若是整数,则根据可知m有最小值.设n为正整数,若是大于1的整数,则n的最小值为 ,最大值为 ,的小数部分为 .
23.已知,则的值为 .
24.设,,当t为 时,代数式.
三、解答题
25.计算
(1); (2);
(3); (4);
(5); (6).
26.(1)已知其中,化简求值;
(2)已知,探究m与n的关系.
27.先化简,再求值
(1),其中,;
(2),其中,.
28.(1)计算:;
(2)已知a、b、c满足.判断以a、b、c为边能否构成三角形?若能构成三角形,说明此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
29.阅读下列材料,然后回答问题.
①在进行二次根式的化简与运算时,我们有时会碰上如一样的式子,可以将其进一步化简:
以上这种化简的步骤叫做分母有理化.
②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算.
(1)计算:.
(2)已知m是正整数,,,,求m.
(3)已知,则的值为
30.【阅读材料】
像,,,两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.
例如,与,与,与 ,等都是互为有理化因式.进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
(1)的有理化因式为 ;
(2)化简:;
(3)①如图,中,与的角平分线相交于点P,若的周长为,面积为3,则点P到边的距离为 .
②已知有理数a、b满足,求a、b的值.
31.先阅读,后解答:
;
像上述解题过程中,与,与相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程中也称为分母有理化
(1)的有理化因式为________;的有理化因式为________.
(2)化简:.
(3)计算:
32.阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如,善于思考的小明进行了以下探索:
若设(其中a、b、m、n均为整数),则有.这样小明就找到了一种把类似的式子化为平方式的方法,请你仿照小明的方法探索并解决下列问题:
(1)若,当a、b、m、n均为整数时,用含m、n的式子分别表示a、b,得:a= ,b= ;
(2)若,且a、m、n均为正整数,求a的值;
(3)化简:.
33.阅读材料:像;;…两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如与,与,与等都是互为有理化因式.在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.例如:;.解答下列问题:
(1)与______互为有理化因式,将分母有理化得______;
(2)①比较大小:______(填,,,或中的一种)
②计算下列式子的值:
③已知正整数a、b满足,求a,b的值.
34.材料一:有这样一类题目:将化简,如果你能找到两个数m、n,使m2+n2=a且mm=,则将a±2将变成m2+n2±2n,即变成(m±n)2开方,从而使得化简.
例如,5±2=3+2±2=()2+()2±2×=( ±)2,所以== ±:
材料二:在进行二次根式的化简时,我们有时会碰到如,,.这样的式子==(一);==(二);===﹣1(三)以上这种化简的步骤叫做分母有理化.
还可以用以下方法化简:====﹣1(四);
请根据材料解答下列问题:
(1)= ;= .
(2)化简: ++…+.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1-14 DBCDD AACBD BBCC
15.
16.
17.3
18.
19.
20.
21.
22. 3 75
23./
24.2
25.(1)解:原式
;
(2)解:原式
.
(3)解:原式
;
(4)解:原式
;
(5)解:原式
;
(6)解:原式
.
26.解:(1)
,
,
原式;
(2)
,
,即,
,
,即,
.
27.(1)原式
当,时,
原式
(2)原式
当,时,
原式
28.解:(1)
=
=
=4;
(2)以a、b、c为边能构成三角形,此三角形的形状是直角三角形,
理由是:
∵a、b、c满足,
∴a﹣2=0,3﹣b=0,c﹣=0,
∴a=2,b=3,c=,
∵2+3>,2+>3,2+>3,
∴以a、b、c为边能组成三角形,
∵a=2,b=3,c=,
∴a2+b2=c2,
∴以a、b、c为边能构成直角三角形,直角边是a和b,
则此三角形的面积是=3.
29.(1)解:
;
(2),,
,,,
,
,
,
;
(3)设,,则,
,
,
,
,
,
,
.(舍去),
.
30.(1)解:根据题意可知:,
∴的有理化因式为;
故答案为:.
(2)
;
(3)①过点分别作边、、的垂线段、、,
中,与的角平分线相交于点,
线段,
,
的周长为,面积为3,
,
解得,
即点P到边的距离为;
②
∴,解得:.
31.(1)解:,,
∴的有理化因式是,的有理化因式是,
故答案为:;;
(2)解:
;
(3)解:(n为正整数)
,
∴
.
32.(1)∵,
∴,
∴.
故答案为:,;
(2)∵,
∴,6=2mn,
∴mn=3.
∵a、m、n均为正整数,
∴m=1,n=3或m=3,n=1.
当m=1,n=3时,;
当m=3,n=1时,.
∴a的值为28或12;
(3)令,
则
∴.
33.(1)解:与互为有理化因式,
,
故答案为:,;
(2)解:①,,
,,
,
,
,
故答案为:;
②
,
;
③
,
,
,
,
,,
.
34.(1)解:∵,
,
∴=,
,
故答案为:,;
(2)解:∵===﹣1,
,
,
,
∴原式=
=.
答案第1页,共2页
答案第1页,共2页
同课章节目录
