探索勾股定理

课件28张PPT。探索勾股定理八年级数学（上册）? 北师版 演示课件，提出问题：事故中的重伤员生命危在旦夕，必须在10分钟之内得到救护，否则…… 那么，接到通知后空中救护组能否及时抵达现场实施救护？
相关资料：A.市空中救护中心救护组得到指令后，一般在5分钟内可以登机。B.救护组直升机起飞和降落均需1分钟时间，其巡航速度（空中飞行速度）为每小时240公里。C.市区地图（局部） 场景：（1）观察图1-1
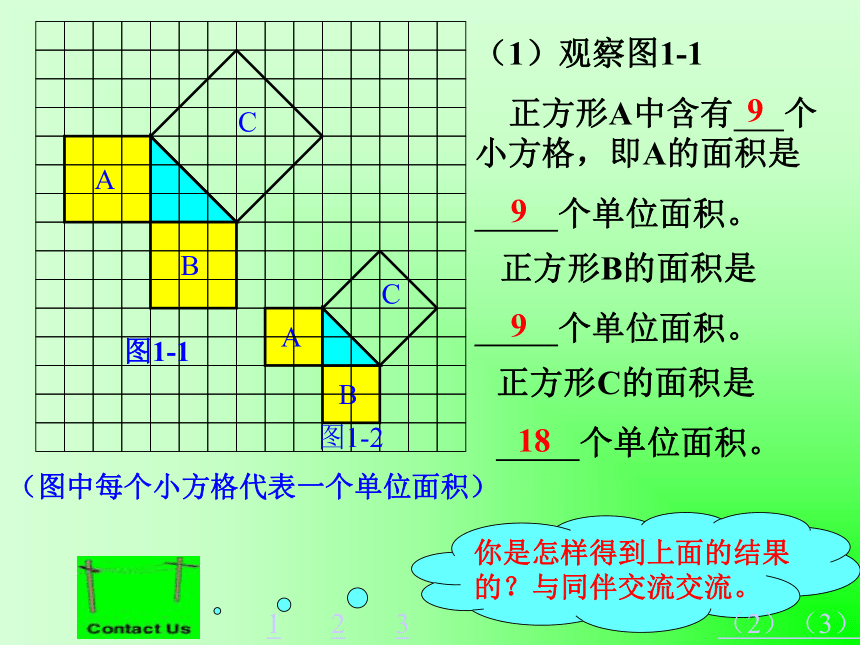
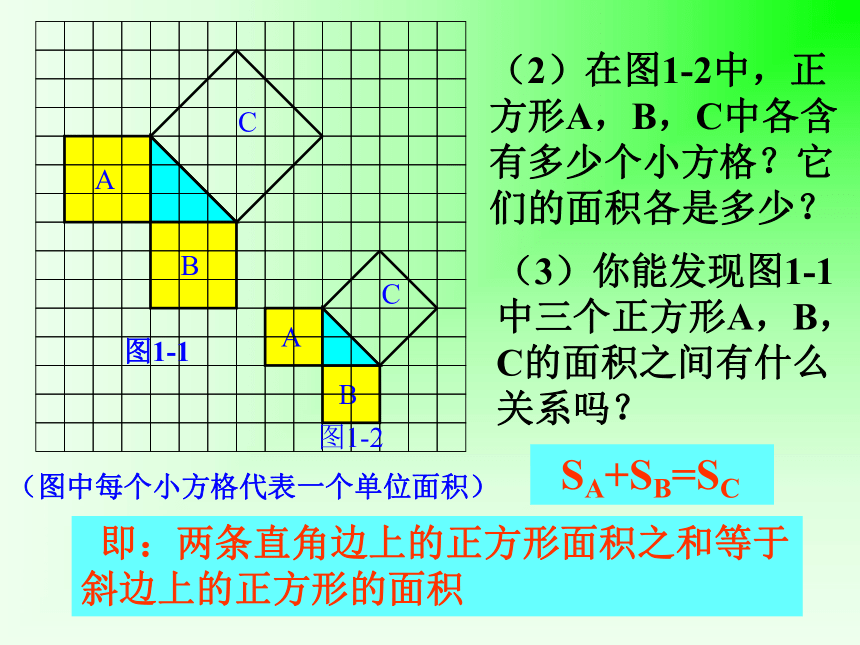
正方形A中含有 个小方格，即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
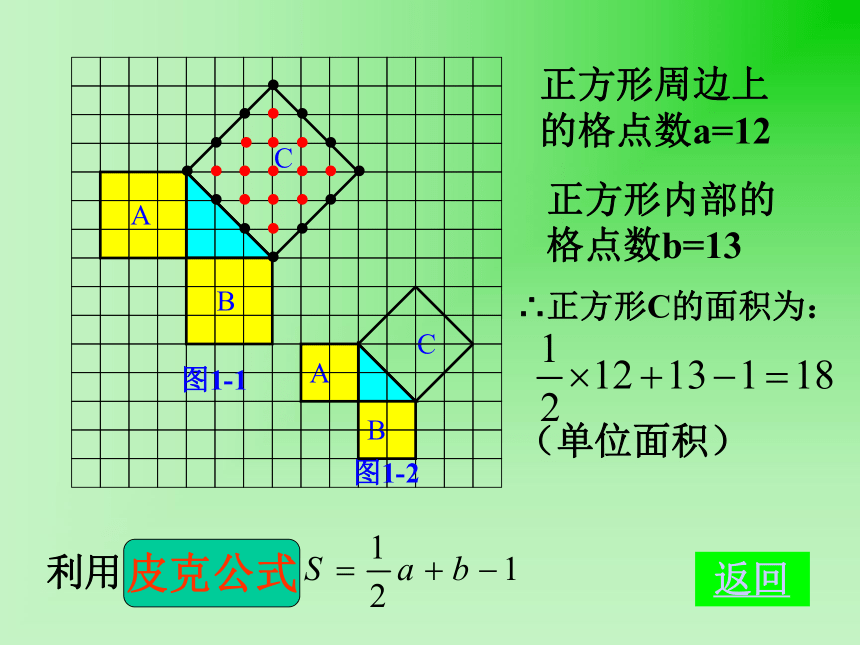
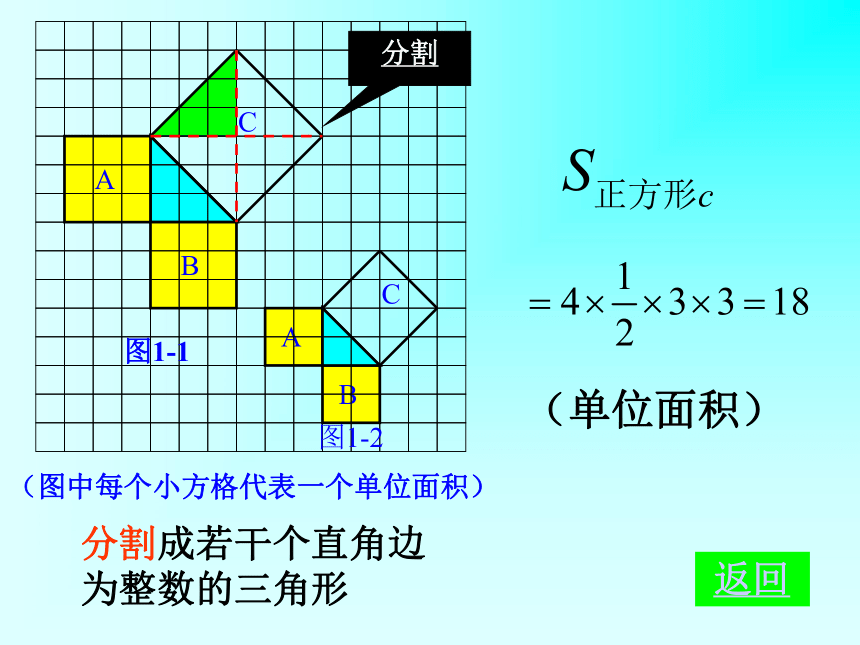
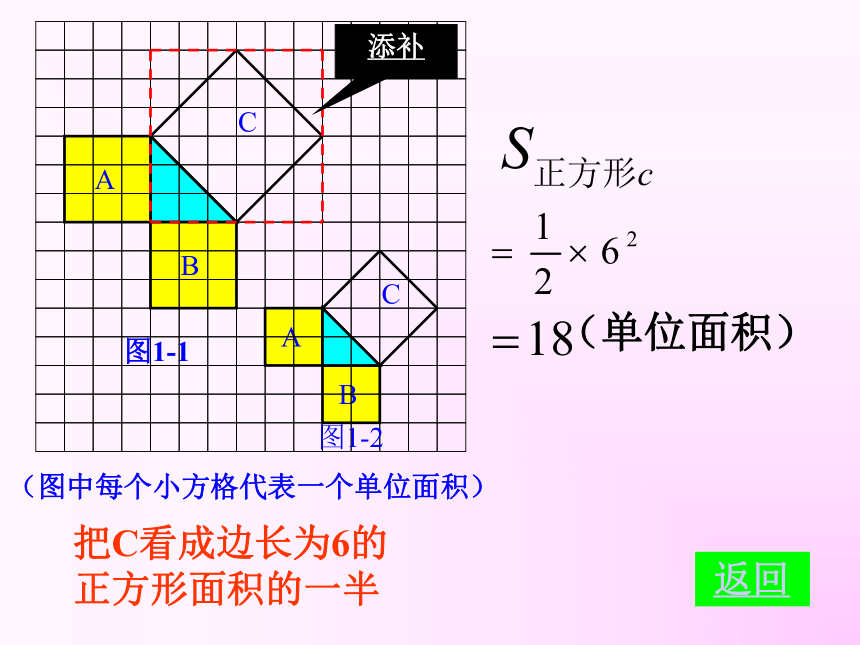
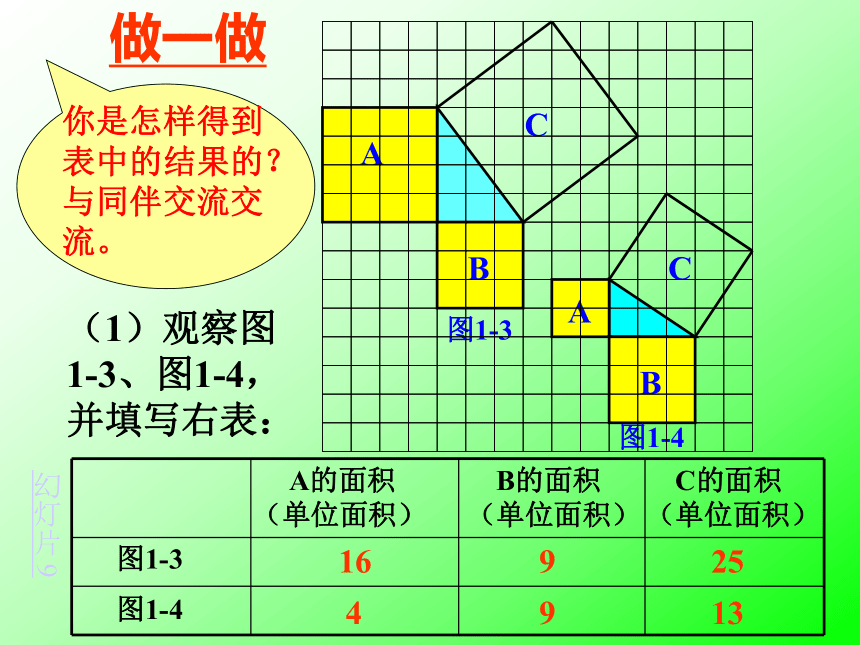
个单位面积。99918123（2）（3）正方形周边上的格点数a=12正方形内部的格点数b=13 返回图1-1图1-2分割成若干个直角边为整数的三角形（单位面积） 返回分割（单位面积）把C看成边长为6的正方形面积的一半 返回添补（2）在图1-2中，正方形A，B，C中各含有多少个小方格？它们的面积各是多少？（3）你能发现图1-1中三个正方形A，B，C的面积之间有什么关系吗？ SA+SB=SC 即：两条直角边上的正方形面积之和等于 斜边上的正方形的面积（1）观察图1-3、图1-4，并填写右表： A的面积（单位面积） B的面积（单位面积） C的面积（单位面积）图1-3图1-4169254913做一做幻灯片 9分割成若干个直角边为整数的三角形（面积单位）幻灯片 7（2）三个正方形A，B，C的面积之间有什么关系？SA+SB=SC
即：两条直角边上的正方形面积之和等于 斜边上的正方形的面积幻灯片 7（1）你能用三角形的边长表示正方形的面积吗？（2）你能发现直角三角形三边长度之间存在什么关系吗？与同伴进行交流。（3）分别以5厘米、12厘米为直角边作出一个直角三角形，并测量斜边的长度。（2）中的规律对这个三角形仍然成立吗？议一议 勾股定理（gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c，那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦勾股定理的由来　　这个定理在中国又称为“商高定理”，在外国称为“毕达哥拉斯定理”。为什么一个定理有这么多名称呢？商高是公元前十一世纪的中国人。当时中国的朝代是西周，是奴隶社会时期。在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说：“…故折矩，勾广三，股修四，经隅五。“什么是”勾、股“呢？在中国古代，人们把弯曲成直角的手臂的上半部分称为“勾”，下半部分称为“股”。商高那段话的意思就是说：当直角三角形的两条直角边分别为3（短边）和4（长边）时，径隅（就是弦）则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。由于勾股定理的内容最早见于商高的话中，所以人们就把这个定理叫作"商高定理"。
　　毕达哥拉斯（Pythagoras）是古希腊数学家，他是公元前五世纪的人，比商高晚出生五百多年。希腊另一位数学家欧几里德（Euclid，是公元前三百年左右的人）在编著《几何原本》时，认为这个定理是毕达哥达斯最早发现的，所以他就把这个定理称为"毕达哥拉斯定理"，以后就流传开了。走进数学史 如图：一块长约120步、宽约50步的长方形麦田，被不自觉的学生沿对角线踏出了一条斜“路”，类似的现象也时有发生。请问同学们：
　　1、走斜“路”的客观原因是什么？为什么？
　　2、斜“路”比正路近多少？这么几步近路，值得用我们的声誉作为代价来换取吗？习题1—11、求下图中字母所代表的正方形的面积。225A400225B81求出下列直角三角形中未知边的长度。68x513y 3、如图，一根旗杆在离地面9米处断裂，旗杆顶部落在离旗杆底部12米处，旗杆折断前有多高。9米12米 4、求斜边长17厘米，一条直角边长15厘米的直角三角形的面积。1715解：设另一条直角边为x厘米，根据勾股定理得；
x2 = 172－152
= 289－225
= 64
x = 8（-8不合题意，舍去）
∴该三角形的面积为：
8×15÷2
=60一个滑梯高5米，长13米。你从梯顶滑落到梯底，水平移动了几米？出奇制胜如图，在直角三角形ABC中，∠C＝90°，
完成下表：A例题讲解：如图，将长为2.5米的梯子AC斜靠在墙上，BC长为0.7米，
求：(1)梯子上端A到墙的底端B的距离AB． 小明的妈妈买了一部29英寸（74厘米）的电视机。小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了。你能解释这是为什么吗？∴售货员没搞错∵想一想荧屏对角线大约为74厘米解决开始提出的问题数学与美小结说说这节课你有什么收获？牛顿——从苹果落地最终确立了万有引力定律　　我们——从朝夕相处的三角板发现了勾股定理　　虽然两者尚不可同日而语　　但探索和发现——终有价值也许就在身边　　也许就在眼前　　还隐藏着无穷的“万有引力定律”和“勾股定理”……　　祝愿同学们——　　修得一个用数学思维思考世界的头脑　　练就一双用数学视角观察世界的眼睛　　开启新的探索——　　发现平凡中的不平凡之谜… 作业：一、P6 习题1.1 第1、2、3、4题二、准备4张全等的直角三角形纸片再见