7.5 解直角三角形(第2课时)课件(共36张PPT) 2024-2025学年苏科版九年级数学下册
文档属性
| 名称 | 7.5 解直角三角形(第2课时)课件(共36张PPT) 2024-2025学年苏科版九年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 40.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-07 20:59:07 | ||
图片预览




文档简介
(共36张PPT)
7.5 解直角三角形(2)
第2课时 构造直角三角形解题
问题情境
什么叫解直角三角形?
对于一个一般的三角形,需要知道三边和三角中几个元素就能确定这个三角形
学习目标
1. 会解含特殊角的非直角三角形;
2.会利用解直角三角形求解能化为直角三角形的简单多边形问题.
例题讲解
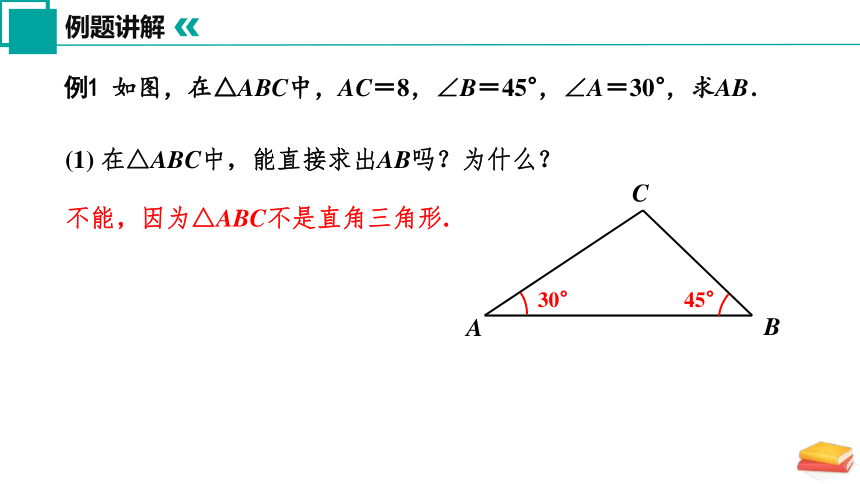
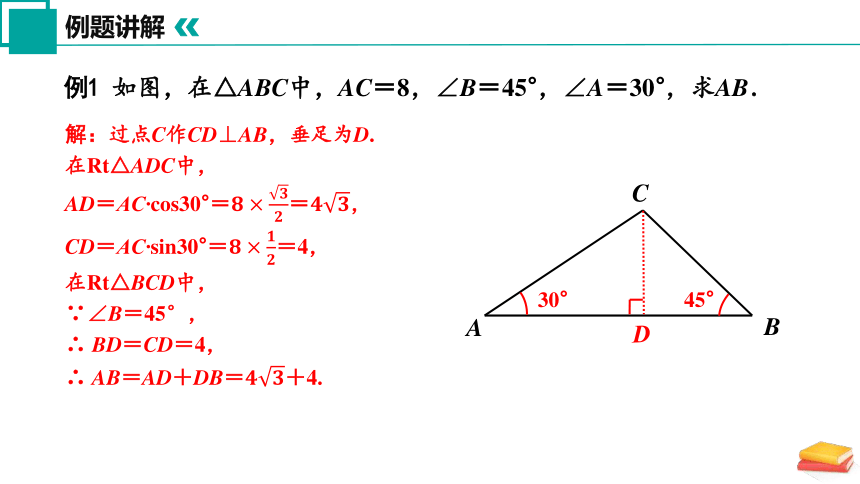
例1 如图,在△ABC中,AC=8,∠B=45°,∠A=30°,求AB.
A
B
C
30°
45°
(1) 在△ABC中,能直接求出AB吗?为什么?
不能,因为△ABC不是直角三角形.
例题讲解
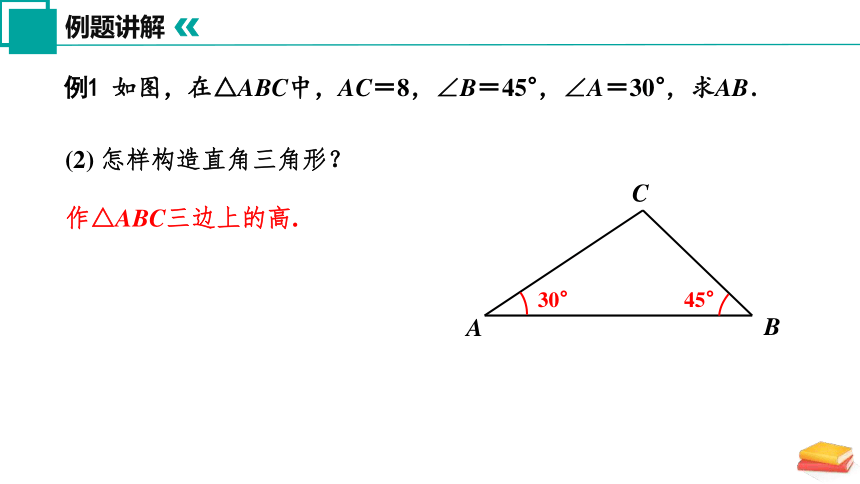
例1 如图,在△ABC中,AC=8,∠B=45°,∠A=30°,求AB.
A
B
C
30°
45°
(2) 怎样构造直角三角形?
作△ABC三边上的高.
(3) 作哪边上的高可以解决问题?
例题讲解
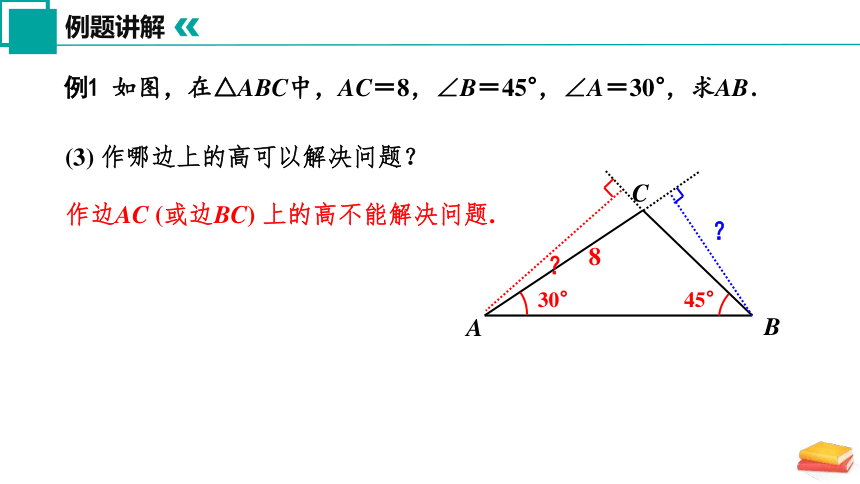
例1 如图,在△ABC中,AC=8,∠B=45°,∠A=30°,求AB.
A
B
C
30°
45°
8
?
?
作边AC (或边BC) 上的高不能解决问题.
例题讲解
例1 如图,在△ABC中,AC=8,∠B=45°,∠A=30°,求AB.
A
B
C
30°
45°
D
解:过点C作CD⊥AB,垂足为D.
在Rt△ADC中,
AD=AC cos30°==,
CD=AC sin30°==4,
在Rt△BCD中,
∵∠B=45°,
∴ BD=CD=4,
∴ AB=AD+DB=+4.
例题讲解
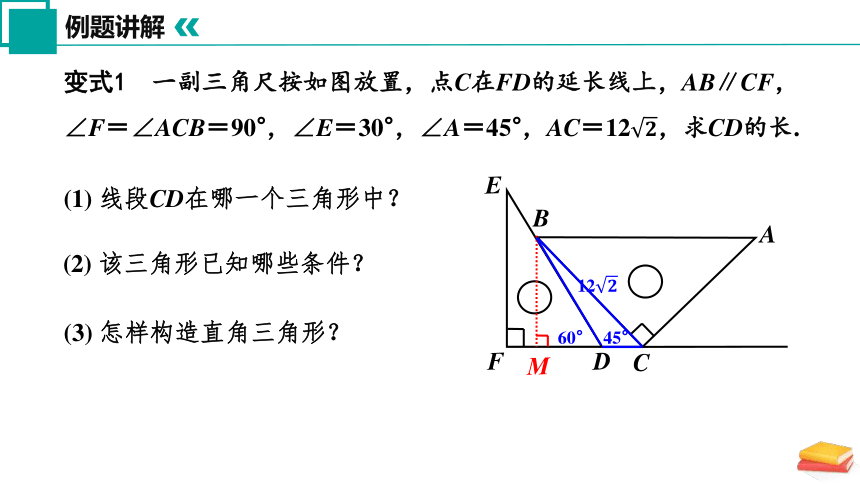
变式1 一副三角尺按如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12,求CD的长.
A
B
C
D
F
E
M
(1) 线段CD在哪一个三角形中?
(2) 该三角形已知哪些条件?
12
45°
60°
(3) 怎样构造直角三角形?
例题讲解
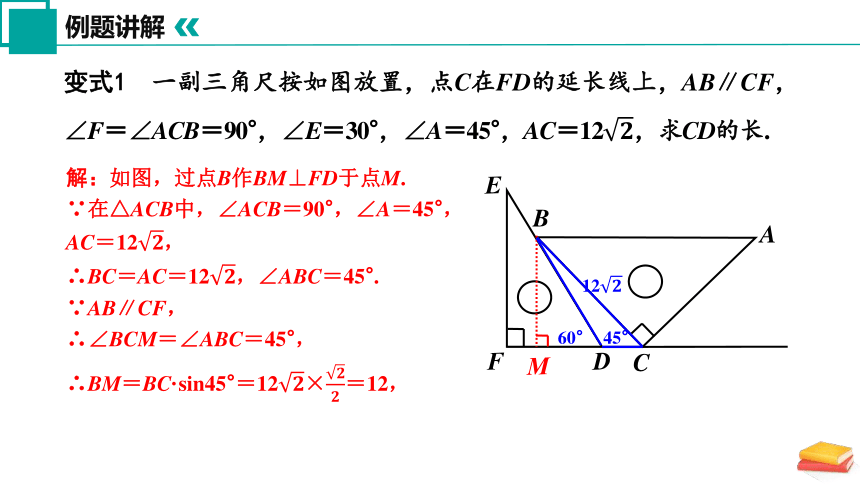
变式1 一副三角尺按如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12,求CD的长.
A
B
C
D
F
E
M
45°
60°
解:如图,过点B作BM⊥FD于点M.
∵在△ACB中,∠ACB=90°,∠A=45°,
AC=12,
∴BC=AC=12,∠ABC=45°.
∵AB∥CF,
∴∠BCM=∠ABC=45°,
∴BM=BC·sin45°=12×=12,
12
例题讲解
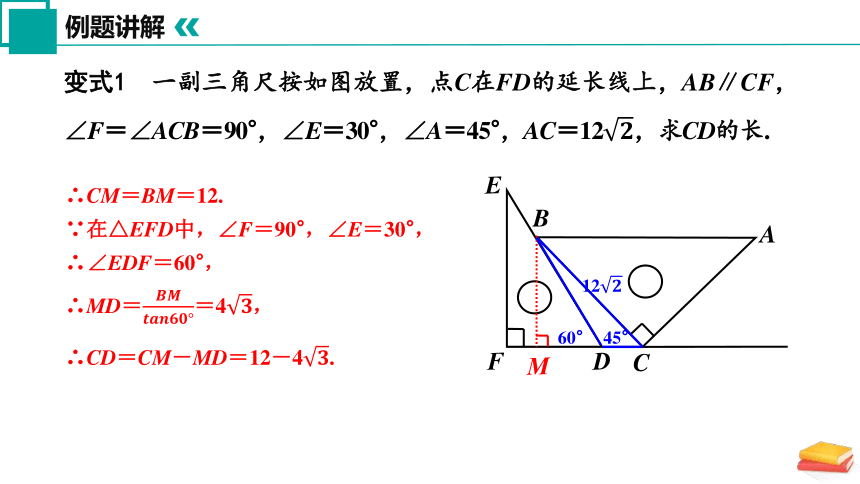
变式1 一副三角尺按如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12,求CD的长.
A
B
C
D
F
E
M
12
45°
60°
∴CM=BM=12.
∵在△EFD中,∠F=90°,∠E=30°,
∴∠EDF=60°,
∴MD==4,
∴CD=CM-MD=12-4.
例题讲解
变式2 在△ABC中,AB=12,AC=13,cosB=,求BC的长.
A
C
B
A
C
B
①
②
D
D
解:∵AB=12,∠B=45°,
∴AD=BD=ABcosB=12×=12,
在Rt△ACD中,由勾股定理得,
CD==5.
当△ABC为锐角三角形时,如图①,
BC=BDCD=125=17.
当△ABC为钝角三角形时,如图②,
BC=BD-CD=12-5=7.
归纳总结
对于非直角三角形问题,往往通过图形的高或作一边上的高,构造直角三角形. 一般情况下是从非特殊角的顶点作高,这样有利于计算.
例题讲解
例2 如图,⊙O的半径为10,求⊙O的内接正五边形ABCDE的边长
(精确到0.1).
H
通过作等腰三角形的高,将等腰三角形转化为直角三角形,借助解直角三角形来解决问题.
D
E
A
B
C
O
例题讲解
例2 如图,⊙O的半径为10,求⊙O的内接正五边形ABCDE的边长
(精确到0.1).
H
解:∵五边形ABCDE是正五边形,
∴∠AOB==72°.
过点O作OH⊥AB,垂足为H.
在Rt△AHO中,
∵∠AHO=90°,∠AOH=∠AOB=36°,OA=10,
∴AH=OA sin36°.
∴正五边形ABCDE的边长AB=2AH=2×10×sin36°≈11.8.
D
E
A
B
C
O
归纳总结
对于正n边形问题,往往作出这个正n边形的外接圆半径和内切圆半径,使得问题化归到直角三角形中,且这个三角形两边(外接圆半径和内切圆半径)的夹角为度,再运用条件解决问题.
新知巩固
1. ABCD中,∠A=60°,AB=8,AD=6,求 ABCD的面积.
A
B
C
D
6
60°
8
E
解:过点D作DE⊥AB,垂足为E.
在Rt△ADE中,
∵∠AED=90°,∠A=60°,AD=6,
∴DE=AD sinA=6×sin60°=.
∴S ABCD=AB×DE=8×=24.
新知巩固
2. 如图,在菱形钢架ABCD中,AB=2m,∠BAD=72°,焊接这个钢架约需多长的钢材(精确到0.1m)
解:∵四边形ABCD是菱形,
∴ AC⊥BD, OA=OC,OB=OD,
∠BAO=∠BAD=36°,
∴OB=AB· sin 36°,OA=AB· cos 36°.
∴焊接这个钢架的长度
=4ABABsin 36°ABcos 36°
=4×22×1.182×1.62≈13.6(m).
答:焊接这个钢架约需13.6m的钢材.
O
新知巩固
3. 求半径为12的圆的内接正八边形的边长(精确到0.1).
A
B
O
H
解:∵八边形ABCDEFGH是正八边形,
∴∠AOB==45°.
过点O作OH⊥AB,垂足为H.
在Rt△AHO中,
∵∠AHO=90°,∠AOH=∠AOB=22.5°,OA=12,
∴AH=OA sin22.5°=12sin22.5°.
∴正五边形ABCDE的边长AB
=2AH=2×12×sin22.5°≈9.2.
C
D
E
F
G
H
新知巩固
4.如图,已知在△ABC中,∠A=45°,∠B=60°,AB=8,求△ABC的面积.
D
A
B
C
解:∵,,
∴,,
∴,
设,则,
∵,∴,
∴,∴,
解得:,
∴,
∴.
含特殊角的非直角三角形
能化为直角三角形的简单多边形问题
课堂总结
正n边形问题
1. 如图,在△ABC中,∠A=105°,∠C=30°,若AB=4 ,则AC的长为 ( )
A. 4 B. 8
C. 4 D. 4
D
当堂检测
基础过关
B
C
B
A
当堂检测
基础过关
D
E
A
B
C
O
2. 如图,圆的内接正五边形ABCDE的边长为a,圆的半径为r,则下列等式成立的是 ( )
A. a=2rsin36° B. a=2rcos36°
C. a=rsin36° D. a=2rsin72°
a
r
H
A
当堂检测
基础过关
3. 如图,在△ABC中,sinB=,∠C=45°,AD=1,则BC的长为
______________.
B
C
A
D
当堂检测
基础过关
4. 如图,在平行四边形ABCD中,对角线AC,BD相交成的锐角α=30°,若AC=8,BD=6,则平行四边形ABCD的面积是_______.
12
B
C
D
A
O
α
E
当堂检测
基础过关
5. 如图,△ABC内接于⊙O,AO=2,BC=2,则∠BAC的度数为________.
A
C
B
D
O
●
2
2
60°
当堂检测
基础过关
解:如图,过点B作BD⊥AC,垂足为D.
在Rt△ABD中,cosA=.
∵cosA=,AB=5,
∴AD=AB·cosA=5×=3,
∴BD==4.
∵AC=AB=5,
∴CD=2,
∴BC==2.
B
C
A
D
6. 如图,已知在△ABC中,AB=AC=5,cosA=.求底边BC的长.
当堂检测
基础过关
A
C
B
●
O
H
解:∵△ABC是正三角形,
∴∠BOC==120°.
过点O作OH⊥BC,垂足为H.
在Rt△BOH中,
∵∠BHO=90°,∠BOH=∠BOC=60°,OB=20,
∴BH=OB sin60°,OH=OB cos60°.
∴△ABC的边长BC=2BH=2×20×sin60°≈34.6.
S△ABC=3××BC×OH=×40×sin60°×20cos60°=519.6.
7. 求半径为20的圆的内接正三角形的边长和面积(精确到0.1).
当堂检测
能力提升
1. 如图,在菱形ABCD中,AE⊥BC于点E,EC=4, sinB=,则菱形的周长是 ( )
A.10 B.20
C.40 D.28
C
B
C
D
A
E
D
当堂检测
能力提升
2. 在△ABC中,AB=2, AC=3,∠B=60°,则BC的长为( )
A. B.
C. D. 1
B
C
A
D
当堂检测
能力提升
3. 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=6,点D是AB边上一点,若tan∠DCB=,则线段DB的长度为________.
C
B
A
D
E
当堂检测
能力提升
4.刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.设半径为1的圆的面积与其内接正n边形的面积差为,如图①,图②,若用圆的内接正八边形和内接正十二边形逼近半径为1的圆,则的值为_____________.
当堂检测
能力提升
5. 如图,在△ABC中,AB=AC,sinB=,延长BC至点D,使CD:AC=1:3,求tan∠CAD的值.
D
B
C
A
E
解:如图,过点D作DE⊥AC,与AC的延长线交于点E,
∵AB=AC,∴∠B=∠ACB.
∵∠DCE=∠ACB,∴∠DCE=∠B.
∵sinB=,∴sin∠DCE==.
不妨设DE=4x,则CD=5x,
∴CE==3x.
∵CD:AC=1:3,∴AC=3CD=15x,
∴AE=AC+CE=18x,
∴tan∠CAD===.
当堂检测
能力提升
6.把圆分成等份,经过各分点作圆的切线,以相邻切线的交点为顶点的多边形叫做这个圆的外切正n边形,如图,⊙O的半径是R,分别求它的外切正三角形、外切正方形、外切正六边形的边长.
O
O
O
B
A
D
B
A
D
B
A
D
当堂检测
能力提升
A
B
O
O
O
B
D
A
D
B
A
D
解:如图,外切正三角形时,∠AOD=360°÷6=60°,
所以,AD=OD tan60°=R R,
所以,外切正三角形边长AB=2AD=2R;
当堂检测
能力提升
A
B
O
O
O
B
D
A
D
B
A
D
外切正方形时,∠AOD=360°÷8=45°,
所以,△AOD是等腰直角三角形,
所以,AD=OD,
外切正方形的边长AB=2AD=2R;
当堂检测
能力提升
A
B
O
O
O
B
D
A
D
B
A
D
外切六边形时,∠AOD=360°÷12=30°,
所以,AD=OD tan30°=R,
所以,外切六边形的边长AB=2AD=R.
7.5 解直角三角形(2)
第2课时 构造直角三角形解题
问题情境
什么叫解直角三角形?
对于一个一般的三角形,需要知道三边和三角中几个元素就能确定这个三角形
学习目标
1. 会解含特殊角的非直角三角形;
2.会利用解直角三角形求解能化为直角三角形的简单多边形问题.
例题讲解
例1 如图,在△ABC中,AC=8,∠B=45°,∠A=30°,求AB.
A
B
C
30°
45°
(1) 在△ABC中,能直接求出AB吗?为什么?
不能,因为△ABC不是直角三角形.
例题讲解
例1 如图,在△ABC中,AC=8,∠B=45°,∠A=30°,求AB.
A
B
C
30°
45°
(2) 怎样构造直角三角形?
作△ABC三边上的高.
(3) 作哪边上的高可以解决问题?
例题讲解
例1 如图,在△ABC中,AC=8,∠B=45°,∠A=30°,求AB.
A
B
C
30°
45°
8
?
?
作边AC (或边BC) 上的高不能解决问题.
例题讲解
例1 如图,在△ABC中,AC=8,∠B=45°,∠A=30°,求AB.
A
B
C
30°
45°
D
解:过点C作CD⊥AB,垂足为D.
在Rt△ADC中,
AD=AC cos30°==,
CD=AC sin30°==4,
在Rt△BCD中,
∵∠B=45°,
∴ BD=CD=4,
∴ AB=AD+DB=+4.
例题讲解
变式1 一副三角尺按如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12,求CD的长.
A
B
C
D
F
E
M
(1) 线段CD在哪一个三角形中?
(2) 该三角形已知哪些条件?
12
45°
60°
(3) 怎样构造直角三角形?
例题讲解
变式1 一副三角尺按如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12,求CD的长.
A
B
C
D
F
E
M
45°
60°
解:如图,过点B作BM⊥FD于点M.
∵在△ACB中,∠ACB=90°,∠A=45°,
AC=12,
∴BC=AC=12,∠ABC=45°.
∵AB∥CF,
∴∠BCM=∠ABC=45°,
∴BM=BC·sin45°=12×=12,
12
例题讲解
变式1 一副三角尺按如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12,求CD的长.
A
B
C
D
F
E
M
12
45°
60°
∴CM=BM=12.
∵在△EFD中,∠F=90°,∠E=30°,
∴∠EDF=60°,
∴MD==4,
∴CD=CM-MD=12-4.
例题讲解
变式2 在△ABC中,AB=12,AC=13,cosB=,求BC的长.
A
C
B
A
C
B
①
②
D
D
解:∵AB=12,∠B=45°,
∴AD=BD=ABcosB=12×=12,
在Rt△ACD中,由勾股定理得,
CD==5.
当△ABC为锐角三角形时,如图①,
BC=BDCD=125=17.
当△ABC为钝角三角形时,如图②,
BC=BD-CD=12-5=7.
归纳总结
对于非直角三角形问题,往往通过图形的高或作一边上的高,构造直角三角形. 一般情况下是从非特殊角的顶点作高,这样有利于计算.
例题讲解
例2 如图,⊙O的半径为10,求⊙O的内接正五边形ABCDE的边长
(精确到0.1).
H
通过作等腰三角形的高,将等腰三角形转化为直角三角形,借助解直角三角形来解决问题.
D
E
A
B
C
O
例题讲解
例2 如图,⊙O的半径为10,求⊙O的内接正五边形ABCDE的边长
(精确到0.1).
H
解:∵五边形ABCDE是正五边形,
∴∠AOB==72°.
过点O作OH⊥AB,垂足为H.
在Rt△AHO中,
∵∠AHO=90°,∠AOH=∠AOB=36°,OA=10,
∴AH=OA sin36°.
∴正五边形ABCDE的边长AB=2AH=2×10×sin36°≈11.8.
D
E
A
B
C
O
归纳总结
对于正n边形问题,往往作出这个正n边形的外接圆半径和内切圆半径,使得问题化归到直角三角形中,且这个三角形两边(外接圆半径和内切圆半径)的夹角为度,再运用条件解决问题.
新知巩固
1. ABCD中,∠A=60°,AB=8,AD=6,求 ABCD的面积.
A
B
C
D
6
60°
8
E
解:过点D作DE⊥AB,垂足为E.
在Rt△ADE中,
∵∠AED=90°,∠A=60°,AD=6,
∴DE=AD sinA=6×sin60°=.
∴S ABCD=AB×DE=8×=24.
新知巩固
2. 如图,在菱形钢架ABCD中,AB=2m,∠BAD=72°,焊接这个钢架约需多长的钢材(精确到0.1m)
解:∵四边形ABCD是菱形,
∴ AC⊥BD, OA=OC,OB=OD,
∠BAO=∠BAD=36°,
∴OB=AB· sin 36°,OA=AB· cos 36°.
∴焊接这个钢架的长度
=4ABABsin 36°ABcos 36°
=4×22×1.182×1.62≈13.6(m).
答:焊接这个钢架约需13.6m的钢材.
O
新知巩固
3. 求半径为12的圆的内接正八边形的边长(精确到0.1).
A
B
O
H
解:∵八边形ABCDEFGH是正八边形,
∴∠AOB==45°.
过点O作OH⊥AB,垂足为H.
在Rt△AHO中,
∵∠AHO=90°,∠AOH=∠AOB=22.5°,OA=12,
∴AH=OA sin22.5°=12sin22.5°.
∴正五边形ABCDE的边长AB
=2AH=2×12×sin22.5°≈9.2.
C
D
E
F
G
H
新知巩固
4.如图,已知在△ABC中,∠A=45°,∠B=60°,AB=8,求△ABC的面积.
D
A
B
C
解:∵,,
∴,,
∴,
设,则,
∵,∴,
∴,∴,
解得:,
∴,
∴.
含特殊角的非直角三角形
能化为直角三角形的简单多边形问题
课堂总结
正n边形问题
1. 如图,在△ABC中,∠A=105°,∠C=30°,若AB=4 ,则AC的长为 ( )
A. 4 B. 8
C. 4 D. 4
D
当堂检测
基础过关
B
C
B
A
当堂检测
基础过关
D
E
A
B
C
O
2. 如图,圆的内接正五边形ABCDE的边长为a,圆的半径为r,则下列等式成立的是 ( )
A. a=2rsin36° B. a=2rcos36°
C. a=rsin36° D. a=2rsin72°
a
r
H
A
当堂检测
基础过关
3. 如图,在△ABC中,sinB=,∠C=45°,AD=1,则BC的长为
______________.
B
C
A
D
当堂检测
基础过关
4. 如图,在平行四边形ABCD中,对角线AC,BD相交成的锐角α=30°,若AC=8,BD=6,则平行四边形ABCD的面积是_______.
12
B
C
D
A
O
α
E
当堂检测
基础过关
5. 如图,△ABC内接于⊙O,AO=2,BC=2,则∠BAC的度数为________.
A
C
B
D
O
●
2
2
60°
当堂检测
基础过关
解:如图,过点B作BD⊥AC,垂足为D.
在Rt△ABD中,cosA=.
∵cosA=,AB=5,
∴AD=AB·cosA=5×=3,
∴BD==4.
∵AC=AB=5,
∴CD=2,
∴BC==2.
B
C
A
D
6. 如图,已知在△ABC中,AB=AC=5,cosA=.求底边BC的长.
当堂检测
基础过关
A
C
B
●
O
H
解:∵△ABC是正三角形,
∴∠BOC==120°.
过点O作OH⊥BC,垂足为H.
在Rt△BOH中,
∵∠BHO=90°,∠BOH=∠BOC=60°,OB=20,
∴BH=OB sin60°,OH=OB cos60°.
∴△ABC的边长BC=2BH=2×20×sin60°≈34.6.
S△ABC=3××BC×OH=×40×sin60°×20cos60°=519.6.
7. 求半径为20的圆的内接正三角形的边长和面积(精确到0.1).
当堂检测
能力提升
1. 如图,在菱形ABCD中,AE⊥BC于点E,EC=4, sinB=,则菱形的周长是 ( )
A.10 B.20
C.40 D.28
C
B
C
D
A
E
D
当堂检测
能力提升
2. 在△ABC中,AB=2, AC=3,∠B=60°,则BC的长为( )
A. B.
C. D. 1
B
C
A
D
当堂检测
能力提升
3. 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=6,点D是AB边上一点,若tan∠DCB=,则线段DB的长度为________.
C
B
A
D
E
当堂检测
能力提升
4.刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.设半径为1的圆的面积与其内接正n边形的面积差为,如图①,图②,若用圆的内接正八边形和内接正十二边形逼近半径为1的圆,则的值为_____________.
当堂检测
能力提升
5. 如图,在△ABC中,AB=AC,sinB=,延长BC至点D,使CD:AC=1:3,求tan∠CAD的值.
D
B
C
A
E
解:如图,过点D作DE⊥AC,与AC的延长线交于点E,
∵AB=AC,∴∠B=∠ACB.
∵∠DCE=∠ACB,∴∠DCE=∠B.
∵sinB=,∴sin∠DCE==.
不妨设DE=4x,则CD=5x,
∴CE==3x.
∵CD:AC=1:3,∴AC=3CD=15x,
∴AE=AC+CE=18x,
∴tan∠CAD===.
当堂检测
能力提升
6.把圆分成等份,经过各分点作圆的切线,以相邻切线的交点为顶点的多边形叫做这个圆的外切正n边形,如图,⊙O的半径是R,分别求它的外切正三角形、外切正方形、外切正六边形的边长.
O
O
O
B
A
D
B
A
D
B
A
D
当堂检测
能力提升
A
B
O
O
O
B
D
A
D
B
A
D
解:如图,外切正三角形时,∠AOD=360°÷6=60°,
所以,AD=OD tan60°=R R,
所以,外切正三角形边长AB=2AD=2R;
当堂检测
能力提升
A
B
O
O
O
B
D
A
D
B
A
D
外切正方形时,∠AOD=360°÷8=45°,
所以,△AOD是等腰直角三角形,
所以,AD=OD,
外切正方形的边长AB=2AD=2R;
当堂检测
能力提升
A
B
O
O
O
B
D
A
D
B
A
D
外切六边形时,∠AOD=360°÷12=30°,
所以,AD=OD tan30°=R,
所以,外切六边形的边长AB=2AD=R.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
