勾股定理的证明

课件40张PPT。勾股定理证明评鉴子杰注曰：本人获教育署数学组之邀请，于 2001 年 6 月 28、29 及 7 月 3 日，就着新的数学课程而举办的研讨会中，发表了约半小时的演讲。
演讲的目的主要是总结几个重要的勾股定理证明，并和与会的老师一同欣赏这些证明妙趣之处，以及了解一下有关证明的历史。
本档为当时辅助演讲的演示档。
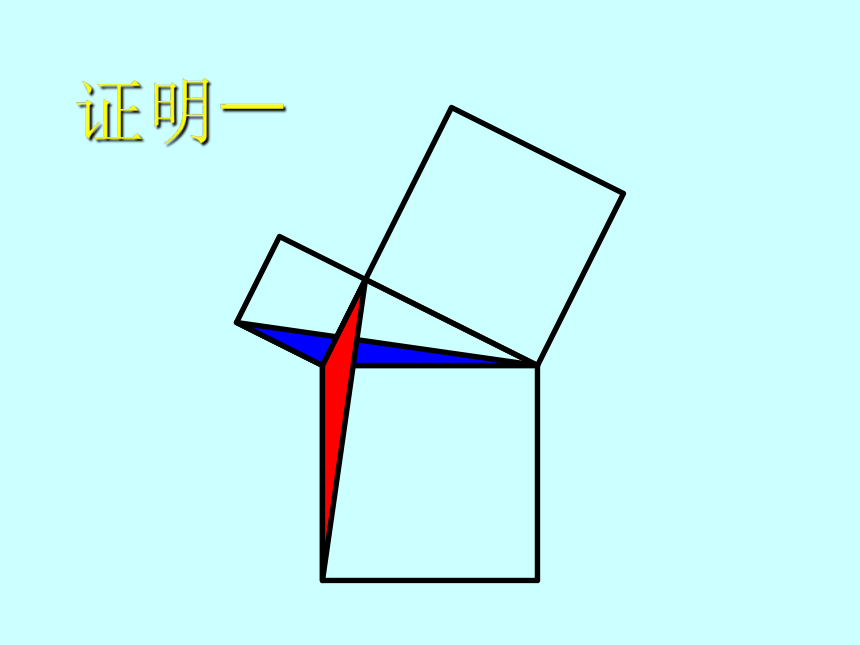
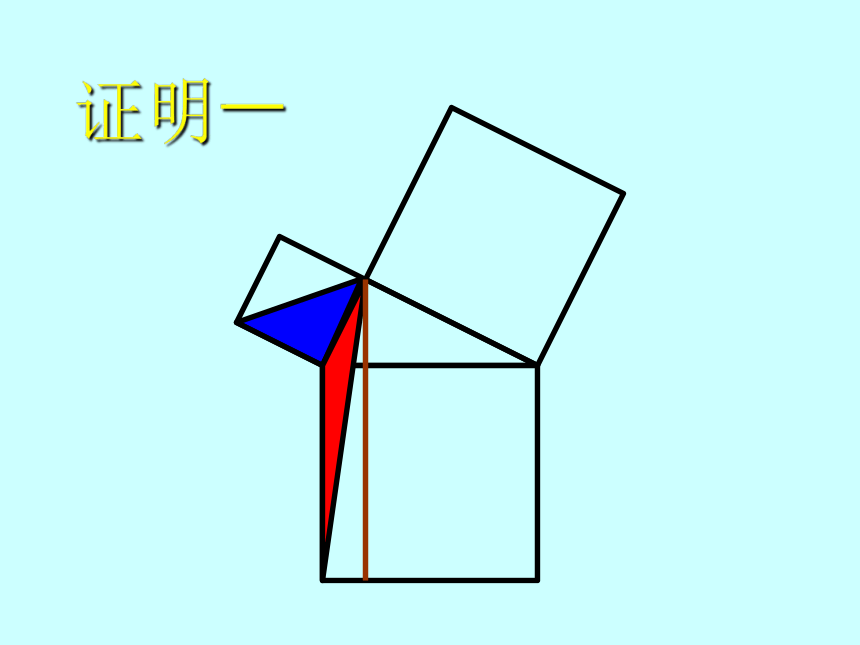
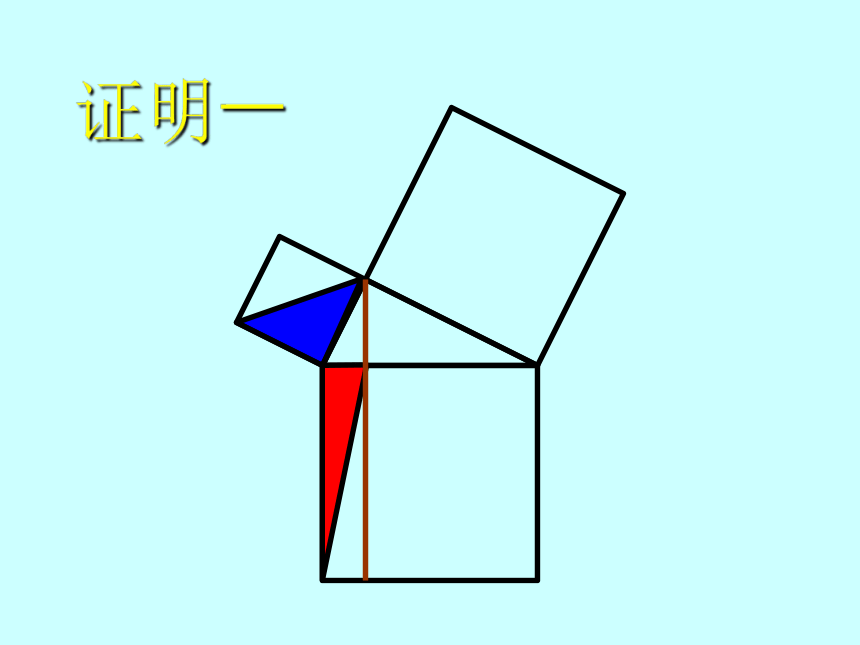
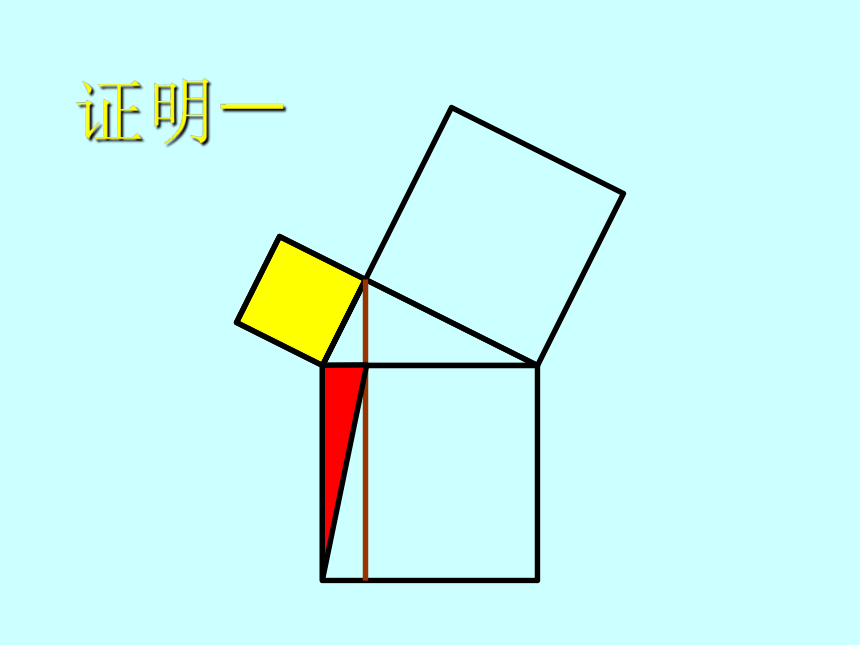
本人强调：这档案只为当时演讲而设计，绝不适宜一般课堂中使用，敬请读者留意！证明一证明一证明一证明一证明一几何原本欧几里得（Euclid of Alexandria; 約 325 B.C. ? 約 265 B.C.）欧几里得的《几何原本》是用公理方法建立演绎数学体系的最早典范。
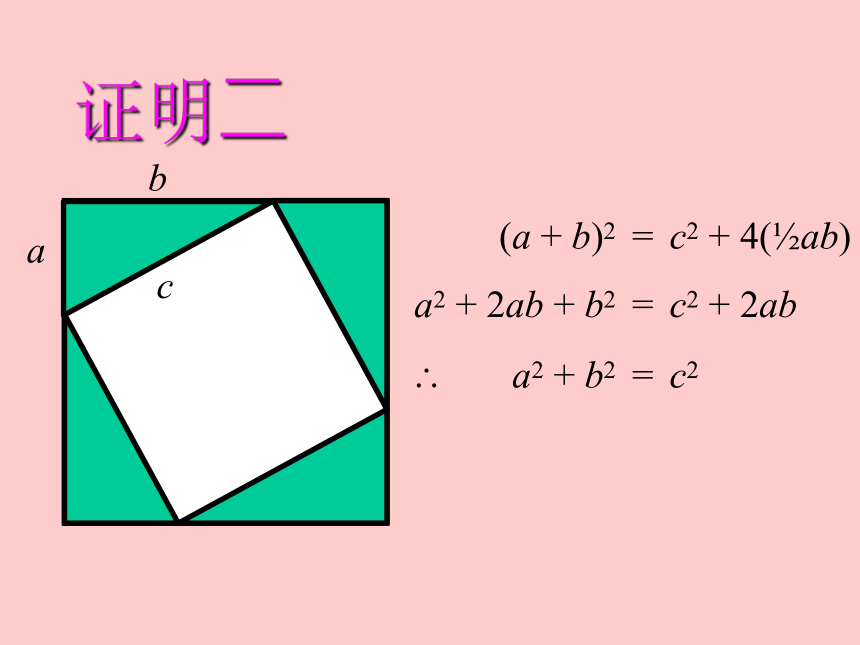
“证明一”就是取材自《几何原本》第一卷的第 47 命题。证明二ba (a + b)2 = c2 + 4(?ab)
a2 + 2ab + b2 = c2 + 2ab
? a2 + b2 = c2c证明二cb ? a c2 = (a ? b)2 + 4(?ab)
= a2 ? 2ab + b2 + 2ab
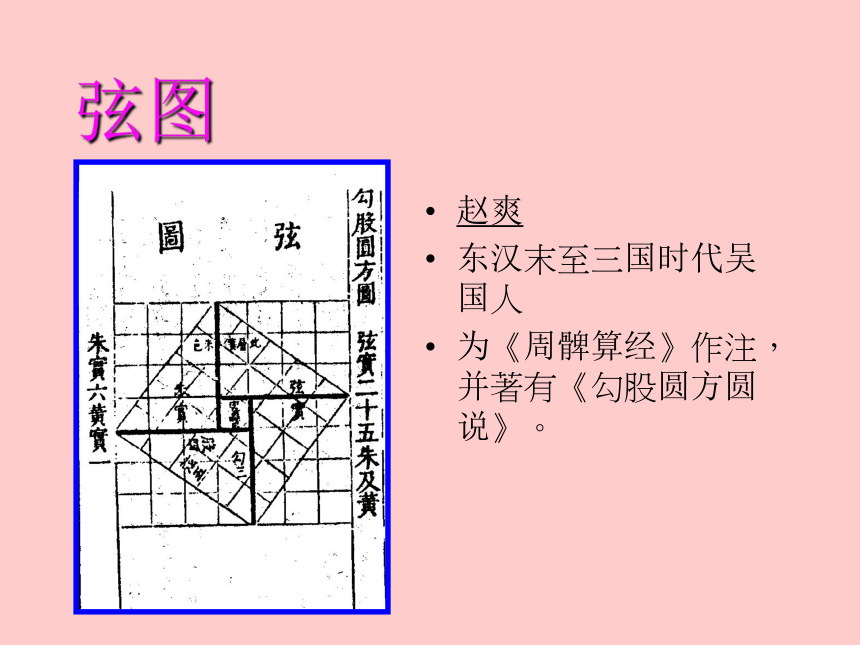
? c2 = a2 + b2弦图赵爽
东汉末至三国时代吴国人
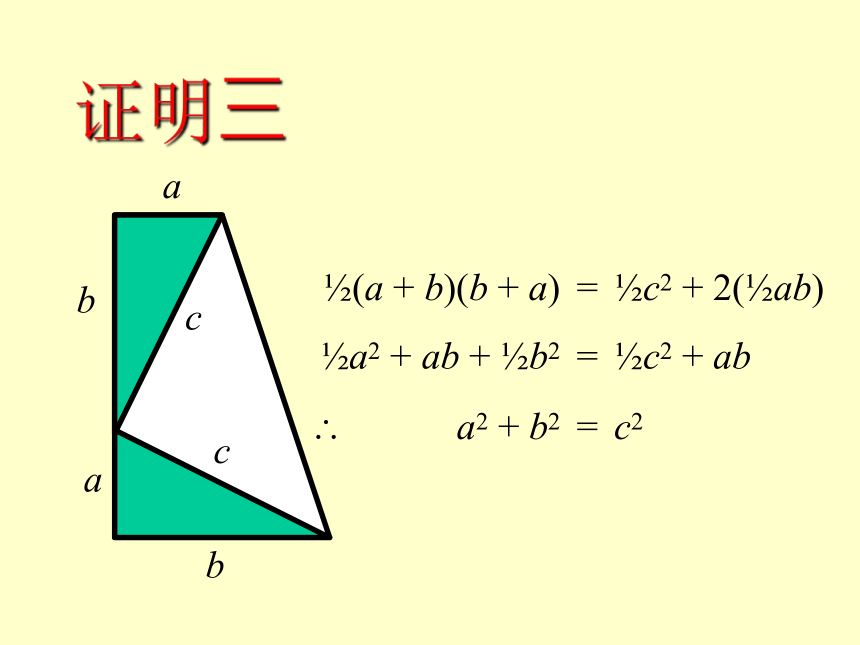
为《周髀算经》作注，并著有《勾股圆方圆说》。证明三 ?(a + b)(b + a) = ?c2 + 2(?ab)
?a2 + ab + ?b2 = ?c2 + ab
? a2 + b2 = c2aabbcc美国总统的证明加菲（James A. Garfield； 1831 ? 1881）1881 年成为美国第 20 任总统
1876 年提出有关证明证明二及证明三的比较两个证明基本上完全相同！ 证明二及证明三的“缺点”两个证明都需要到以下恒等式：
(a ? b)2 = a2 ? 2ab + b2 a2b2证明四证明四证明四证明四证明四c2? a2 + b2 = c2出入相补刘徽（生于公元三世纪）三国魏晋时代人。
魏景元四年（即 263 年）为古籍《九章算术》作注释。
在注作中，提出以“出入相补”的原理来证明“勾股定理”。后人称该图为“青朱入出图”。拼图游戏拼圖遊戲证明五c2证明五证明五证明五a2b2? a2 + b2 = c2无字证明sin(a + b) = sin a cos b + sin b cos a印度婆什迦罗的证明? c2 = b2 + a2证明六注意：
面积 I : 面积 II : 面积 III= a2 : b2 : c2 面积六IIIIII注意：
面积 I : 面积 II : 面积 III= a2 : b2 : c2 证明六IIIIII注意：
面積 I : 面積 II : 面積 III= a2 : b2 : c2 证明六注意：
面积 I : 面积 II : 面积 III= a2 : b2 : c2 证明六注意：
面积 I : 面积 II : 面积 III= a2 : b2 : c2 证明六注意：
面积 I : 面积 II : 面积 III= a2 : b2 : c2 证明六注意：
面积 I : 面积 II : 面积 III= a2 : b2 : c2 由此得，面积 I + 面积 II = 面积 III
因此，a2 + b2 = c2 。 请访以下网页香港道教联合会青松中学网页
http://www.ccss.edu.hk
梁子杰网上文集
http://jckleung.ccss.edu.hk
History of Mathematics
http://www-history.mcs.st-and.ac.uk/~history/
Math Education and Technology International Education Software
www.ies.co.jp/math/java/geo/pythagoras.html完多谢！