8.6 一元二次方程的应用(学案含答案)
文档属性
| 名称 | 8.6 一元二次方程的应用(学案含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 374.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-07 15:19:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第八章 一元二次方程
6 一元二次方程的应用
列清单·划重点
知识点1 列一元二次方程解应用题的步骤
列一元二次方程解应用题的步骤可以归纳为:审、找、设、列、解、验、答.其具体过程是:
(1)审题:阅读题目,明确已知量与未知量;
(2)找 :寻找已知量和未知量之间的联系,用运算符号和等号连接;
(3)设 :一是直接设所求的量为x,二是间接设与所求的量紧密相关且起着关键性作用的量为x,注意设未知数要带单位;
(4)列 :用含有x的代数式把等量关系中的各个量表示出来,列出方程;
(5)解 :选择合适的方法解方程;
(6) :检验两个解是否符合题意,舍去不符合题意的解;
(7)写 .
知识点2 列一元二次方程解应用题的常见类型
1.面积问题.
2.平均增长率(降低率)问题:
变化前的基数(a),增长率或降低率(x),变化的次数(n),变化后的基数(b),这四者之间的关系可用公式 a(1±x) =b表示.
3.利润问题:
单利润= .
总利润=总售价-总进价= .
4.与几何图形结合.
5.动点问题:
这类问题的特点是图形中的某个元素,按照某种规律在运动,但不管是点在运动,还是线在运动,或图形在运动,解题时不要被“动”所迷惑,而应在动中求静,寻求确定的关系式,就能找到解决问题的途径.
明考点·识方法
考点1 几何图形问题
典例1 某校为了美化校园,准备在一块长32米、宽20米的长方形场地上修筑若干条等宽道路,余下部分作草坪,使草坪面积为540平方米,并请全校同学参与设计,现在有两位学生各设计了一种方案(如图),请你根据两种设计方案各列出方程,求图1图2中道路的宽分别是多少
思路导析 图1:设道路的宽为x米.草坪长应该为(32-2x)米,宽应该为(20-2x)米;那么根据草坪的面积为540平方米,即可得出方程,求解即可;图2:如果设路宽为x 米,草坪的长应该为(32-x)米,宽应该为(20-x)米;那么根据草坪的面积为540平方米,即可得出方程,求解即可.
变式 如图,老李想用长为70 m的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈 ABCD,并在边 BC上留一个2m 宽的门(建在EF 处,另用其他材料).
(1)当羊圈的长和宽分别为多少米时,能围成一个面积为640 m 的羊圈
(2)羊圈的面积能达到650 m 吗 如果能,请你给出设计方案;如果不能,请说明理由.
考点2 平均增长 (降低)率问题
典例2 为建设美丽城市,改造老旧小区.某市 2021年投入资金1000 万元,2023 年投入资金 1440 万元.现假定每年投入的资金年增长率相同.
(1)求该市改造老旧小区投入资金的年平均增长率;
(2)2023 年老旧小区改造的平均费用为每个小区96万元,2024年为提高老旧小区品质,每个小区改造费用增加50%.如果投入资金的年平均增长率保持不变,那么该市在2024年最多可以改造多少个老旧小区
思路导析 (1)设该市改造老旧小区投入资金的年平均增长率为x,列出方程 1440,解答即可;
(2)设该市在2024年可以改造y个老旧小区,列出不等式96×(1+50%)y≤1440×(1+20%),解答即可.
变式 为了减轻老百姓医疗负担,某制药厂将一种药剂价格逐年降低.2022 年这种药剂价格为 400 元,2024年该药剂价格为196元.
(1)求2022年到2024年这种药剂价格的年平均下降率;
(2)该制药厂计划 2025年对此药剂继续降价,并要求此种药剂的价格不低于 147元,则此次价格的下降率最多是多少
考点3 营销利润问题
典例3 某特产专卖店销售某种特产,其进价为每千克 40 元,按每千克 60 元出售,平均每天可售出 100千克,经过市场调查发现,单价每降低1元,平均每天的销售量可增加10千克.专卖店销售这种特产若想要平均每天获利2240元,且销售量尽可能大,则每千克特产应定价为多少元
(1)解:方法1:设每千克特产应降价x元,由题意,得方程为 ;
方法2:设每千克特产降低后定价为x元,由题意,得方程为______________________.
(2)请你选择一种方法,写出完整的解答过程.
思路导析 (1)方法1:设每千克特产应降价x元,则销售量为(100+10x),每件利润为(60-x-40)元,利用销售量×每件利润=2240元列出方程即可;
方法2:设每千克特产降价后定价为x元,则销售量为[100+10(60-x)]亻件,每件利润为(x-40)元,利用销售量×每件利润=2240元列出方程即可.
(2)利用(1)中所列方程求出答案.
变式 某商店销售某种商品,平均每天可售出30件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低0.5元,平均每天可多售出2件.
(1)若降价 3 元,则平均每天销售数量为 件;
(2)当每件商品降价多少元时,该商店每天销售利润为2100元
考点4 动态几何问题
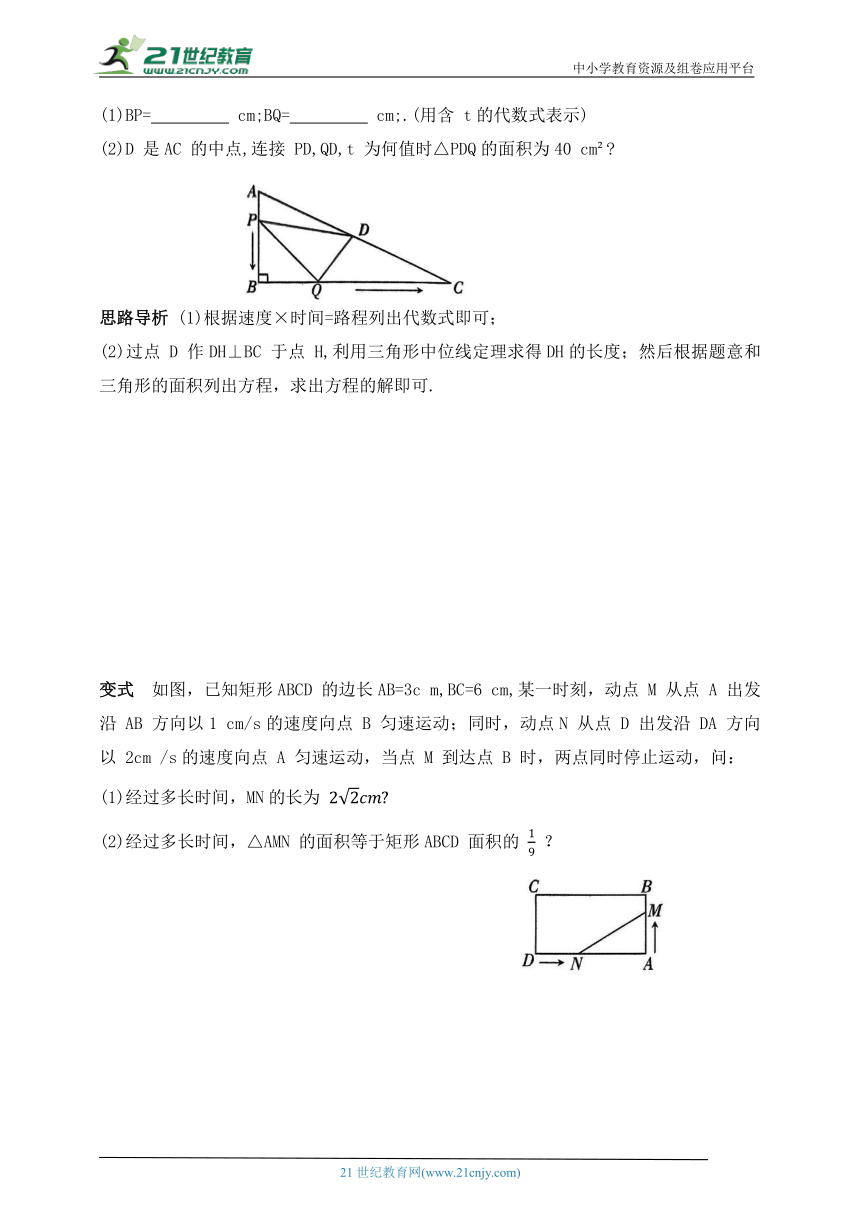
典例 4 如图,在△ABC中,∠B=90°,AB=12 cm,BC=24 cm,动点 P 从点 A 出发沿边 AB 向点 B以2cm/s的速度移动,同时动点 Q从点B出发沿边 BC 向点 C 以 4 cm/s的速度移动,当P 运动到 B 点时,P,Q两点同时停止运动,设运动时间为 ts.
(1)BP= cm;BQ= cm;.(用含 t的代数式表示)
(2)D 是AC 的中点,连接 PD,QD,t 为何值时△PDQ的面积为40 cm
思路导析 (1)根据速度×时间=路程列出代数式即可;
(2)过点 D 作DH⊥BC 于点 H,利用三角形中位线定理求得DH的长度;然后根据题意和三角形的面积列出方程,求出方程的解即可.
变式 如图,已知矩形ABCD 的边长AB=3c m,BC=6 cm,某一时刻,动点 M 从点 A 出发沿 AB 方向以1 cm/s的速度向点 B 匀速运动;同时,动点N 从点 D 出发沿 DA 方向以 2cm /s的速度向点 A 匀速运动,当点 M 到达点 B 时,两点同时停止运动,问:
(1)经过多长时间,MN的长为
(2)经过多长时间,△AMN 的面积等于矩形ABCD 面积的 ?
当堂测·夯基础
1.为了改善居民生活环境,云宁小区对一块矩形空地进行绿化,这块空地的长比宽多6米,面积为720平方米,设矩形空地的长为x 米,根据题意,所列方程正确的是 ( )
2.眉山市东坡区永丰村是“天府粮仓”示范区,该村的“智慧春耕”让生产更高效,提升了水稻亩产量,水稻亩产量从 2021年的 670 千克增长到了2023年的780 千克,该村水稻亩产量年平均增长率为x,则可列方程为 ( )
3.如图所示,在△ABC中,∠B=90°,AB=6 cm,BC=8cm ,点 P 从 A 点开始沿 AB 向 B 点以l cm/s的速度移动,点 Q 从 B 点开始沿BC 边向C 点以 2cm /s的速度移动.如果点 P,Q分别从A,B同时出发,当点 Q到达点 C 时,两点同时停止运动,那么 秒后,线段 PQ将△ABC分成面积1:2的两部分.
4.为增强学生身体素质,提高学生篮球运动竞技水平,扬州市开展“市长杯”篮球比赛,赛制为单循环形式(每两队之间赛一场).现计划赛程3天,每天安排5场比赛,则应邀请 个球队参赛.
5.在过去的 2023年,直播电商一词,我们并不陌生.原本以内容为主的视频平台在入局电商后,大力开拓直播带货模式,并实现高速增长.某电商对一款成本价为 40 元的小商品进行直播销售,如果按每件 60 元销售,每天可卖出 20 件.通过市场调查发现,每件小商品售价每降低 5元,日销售量增加10件.若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为 元.
6.一村民在 2021 年承包种植橙子树 200 亩,由于第一年收成不错,该村民每年都增加种植面积,到2023年,共种植288亩.
(1)求该村民这两年种植橙子亩数的年平均增长率;
(2)某水果批发店销售该种橙子,市场调查发现,当橙子售价为18 元/千克时,每天能售出 120 千克,售价每降低 2元,每天可多售出 30千克,为了减少库存,该店决定降价促销,已知该橙子的平均成本价为8元/千克,若使销售该种橙子每天获利840元,则售价应降低多少元
参考答案
【列清单·划重点】
知识点1 (2)等量关系 (3)未知数 (4)方程 (5)方程 (6)检验 (7)答
知识点2 3.售价一进价 单利润×数量
【明考点·识方法】
典例1
解:图1:设道路的宽为x米.依题意得(32-2x)(20-2x)=540,
整理得 即(x-1)(x-25)=0,
解得 (不合题意舍去).
答:道路宽为1米;
图2:设道路的宽为x米.依题意得(32-x)(20-x)=540,
整理得 即((x-2)(x-50)=0,
解得 (不合题意舍去).
答:道路宽为2米.
变式
解:(1)设矩形ABCD的边AB= xm,则边BC=70-2x+2=(72-2x)m.
根据题意,得x(72-2x)=640,化简,得
解得
当x=16时,72-2x=72-32=40(m),
当x=20时,72-2x=72-40=32(m).
答:当羊圈的长为40 m,宽为16 m或长为32m,宽为 20 m时,能围成一个面积为640 m 的羊圈;
(2)不能,
理由:由题意,得x(72-2x)=650,化简,得
∴一元二次方程没有实数根.
∴羊圈的面积不能达到 650 m .
典例2
解:(1)设该市改造老旧小区投入资金的年平均增长率为x,
依题意得1000(1+x) =1440,解得x =0.2=20%,x =-2.2(不符合题意,舍去).
答:该市改造老旧小区投入资金的年平均增长率为20%;
(2)设该市在 2024年可以改造 y个老旧小区,
依题意得 96×(1+50%)y≤1 440×(1+20%),解得 y≤12,
∴y的最大值为12.
答:该市在2024年最多可以改造12个老旧小区.
变式
解:(1)设2022年到 2024年这种药剂价格的年平均下降率为x,
根据题意得解得(不符合题意,舍去),
答:2022年到 2024年这种药剂价格的年平均下降率为30%;
(2)设此次价格的下降率是 y,
根据题意得196(1-y)≥147,解得 y≤0.25,∴y的最大值是0.25=25%.
答:此次价格的下降率最多是25%.
典例3
解:(1)方法1:设每千克特产应降价x元.根据题意,得
(60-x-40)(100+10x)=2240.
方法2:设每千克特产降价后定价为x元,
由题意,得(x-40)[100+10(60-x)]=2240,
故答案为:(60-x-40)(100+10x)=2 240,(x-40)[100+10(60-x)]=2 240;
(2)方法1:设每千克特产应降价x元.
根据题意,得(60-x-40)(100+10x)=2240,解得
要让销售量尽可能大,只能取x=6,60-6=54(元),
答:每千克特产应定价 54元.
方法2:设每千克特产降价后定价为x元,
由题意,得(x-40)[100+10(60-x)]=2240,解得
要让销售量尽可能大,只能取x=54,答:每千克特产应定价54元.
变式
解:(1)根据题意得 2=30+12=42(件),
∴平均每天销售数量为42件.
故答案为:42;
(2)设每件商品降价x元,则每件的销售利润为(40-x)元,平均每天的销售量为30+ 件,根据题意得(40-x)(30+4x)=2100,
整理得 解得
当x=10时,40-x=40-10=30>25,符合题意;
当 时: 不符合题意,舍去.
答:每件商品应降价 10元.
典例4
解:(1)根据题意得AP=2tcm,BQ=4tcm,所以 BP=(12-2t) cm,
故答案为:(12-2t);4t;
(2)如图,过点 D作DH⊥BC于点 H,
∵∠B=90°,即AB⊥BC.∴AB∥DH.
又∵D是AC的中点,DH是△ABC的中位线.
根据题意,得
整理,得t -6t+8=0.解得
即当 t = 2 或 4 时,△PDQ 的面 积是40 cm .
变式
解:(1)设经过 ts后,则 DN=2tcm,AN=(6 - 2t)cm, AM=tcm,MN的长为
根据题意,由勾股定理得AN +AM =MN ,即
解得
答:经过 2 s 或 s 之后,MN 的长为2 cm;
(2)设经过x秒,△AMN 的面积等于矩形ABCD 面积的
由题意得 DN=2x cm,AN=(6-2x) cm,AM= xcm,
∵矩形 ABCD中,AB=3cm,BC=6cm,
∴矩形 ABCD 的面积为AB·BC=3×6=18(cm ),
∴△AMN的面积
整理得 解得
答:经过1秒或2秒,△AMN的面积等于矩形ABCD面积的
【当堂测·夯基础】
1. A 2. B 3. 2或4 4. 6 5. 50
6.解:(1)设该村民这两年种植橙子亩数的年平均增长率为x,
根据题意,得
解得x =0.2=20%,x =-2.2(不符合题意,舍去).
答:该村民这两年种植橙子亩数的年平均增长率为20%;
(2)设售价应降价 y元,则每千克的销售利润为(18-y-8)元,每天能售出 千克,
根据题意,得 840,
整理得 解得y =6,y =-4(不符合题意,舍去).
答:售价应降低6元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 一元二次方程
6 一元二次方程的应用
列清单·划重点
知识点1 列一元二次方程解应用题的步骤
列一元二次方程解应用题的步骤可以归纳为:审、找、设、列、解、验、答.其具体过程是:
(1)审题:阅读题目,明确已知量与未知量;
(2)找 :寻找已知量和未知量之间的联系,用运算符号和等号连接;
(3)设 :一是直接设所求的量为x,二是间接设与所求的量紧密相关且起着关键性作用的量为x,注意设未知数要带单位;
(4)列 :用含有x的代数式把等量关系中的各个量表示出来,列出方程;
(5)解 :选择合适的方法解方程;
(6) :检验两个解是否符合题意,舍去不符合题意的解;
(7)写 .
知识点2 列一元二次方程解应用题的常见类型
1.面积问题.
2.平均增长率(降低率)问题:
变化前的基数(a),增长率或降低率(x),变化的次数(n),变化后的基数(b),这四者之间的关系可用公式 a(1±x) =b表示.
3.利润问题:
单利润= .
总利润=总售价-总进价= .
4.与几何图形结合.
5.动点问题:
这类问题的特点是图形中的某个元素,按照某种规律在运动,但不管是点在运动,还是线在运动,或图形在运动,解题时不要被“动”所迷惑,而应在动中求静,寻求确定的关系式,就能找到解决问题的途径.
明考点·识方法
考点1 几何图形问题
典例1 某校为了美化校园,准备在一块长32米、宽20米的长方形场地上修筑若干条等宽道路,余下部分作草坪,使草坪面积为540平方米,并请全校同学参与设计,现在有两位学生各设计了一种方案(如图),请你根据两种设计方案各列出方程,求图1图2中道路的宽分别是多少
思路导析 图1:设道路的宽为x米.草坪长应该为(32-2x)米,宽应该为(20-2x)米;那么根据草坪的面积为540平方米,即可得出方程,求解即可;图2:如果设路宽为x 米,草坪的长应该为(32-x)米,宽应该为(20-x)米;那么根据草坪的面积为540平方米,即可得出方程,求解即可.
变式 如图,老李想用长为70 m的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈 ABCD,并在边 BC上留一个2m 宽的门(建在EF 处,另用其他材料).
(1)当羊圈的长和宽分别为多少米时,能围成一个面积为640 m 的羊圈
(2)羊圈的面积能达到650 m 吗 如果能,请你给出设计方案;如果不能,请说明理由.
考点2 平均增长 (降低)率问题
典例2 为建设美丽城市,改造老旧小区.某市 2021年投入资金1000 万元,2023 年投入资金 1440 万元.现假定每年投入的资金年增长率相同.
(1)求该市改造老旧小区投入资金的年平均增长率;
(2)2023 年老旧小区改造的平均费用为每个小区96万元,2024年为提高老旧小区品质,每个小区改造费用增加50%.如果投入资金的年平均增长率保持不变,那么该市在2024年最多可以改造多少个老旧小区
思路导析 (1)设该市改造老旧小区投入资金的年平均增长率为x,列出方程 1440,解答即可;
(2)设该市在2024年可以改造y个老旧小区,列出不等式96×(1+50%)y≤1440×(1+20%),解答即可.
变式 为了减轻老百姓医疗负担,某制药厂将一种药剂价格逐年降低.2022 年这种药剂价格为 400 元,2024年该药剂价格为196元.
(1)求2022年到2024年这种药剂价格的年平均下降率;
(2)该制药厂计划 2025年对此药剂继续降价,并要求此种药剂的价格不低于 147元,则此次价格的下降率最多是多少
考点3 营销利润问题
典例3 某特产专卖店销售某种特产,其进价为每千克 40 元,按每千克 60 元出售,平均每天可售出 100千克,经过市场调查发现,单价每降低1元,平均每天的销售量可增加10千克.专卖店销售这种特产若想要平均每天获利2240元,且销售量尽可能大,则每千克特产应定价为多少元
(1)解:方法1:设每千克特产应降价x元,由题意,得方程为 ;
方法2:设每千克特产降低后定价为x元,由题意,得方程为______________________.
(2)请你选择一种方法,写出完整的解答过程.
思路导析 (1)方法1:设每千克特产应降价x元,则销售量为(100+10x),每件利润为(60-x-40)元,利用销售量×每件利润=2240元列出方程即可;
方法2:设每千克特产降价后定价为x元,则销售量为[100+10(60-x)]亻件,每件利润为(x-40)元,利用销售量×每件利润=2240元列出方程即可.
(2)利用(1)中所列方程求出答案.
变式 某商店销售某种商品,平均每天可售出30件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低0.5元,平均每天可多售出2件.
(1)若降价 3 元,则平均每天销售数量为 件;
(2)当每件商品降价多少元时,该商店每天销售利润为2100元
考点4 动态几何问题
典例 4 如图,在△ABC中,∠B=90°,AB=12 cm,BC=24 cm,动点 P 从点 A 出发沿边 AB 向点 B以2cm/s的速度移动,同时动点 Q从点B出发沿边 BC 向点 C 以 4 cm/s的速度移动,当P 运动到 B 点时,P,Q两点同时停止运动,设运动时间为 ts.
(1)BP= cm;BQ= cm;.(用含 t的代数式表示)
(2)D 是AC 的中点,连接 PD,QD,t 为何值时△PDQ的面积为40 cm
思路导析 (1)根据速度×时间=路程列出代数式即可;
(2)过点 D 作DH⊥BC 于点 H,利用三角形中位线定理求得DH的长度;然后根据题意和三角形的面积列出方程,求出方程的解即可.
变式 如图,已知矩形ABCD 的边长AB=3c m,BC=6 cm,某一时刻,动点 M 从点 A 出发沿 AB 方向以1 cm/s的速度向点 B 匀速运动;同时,动点N 从点 D 出发沿 DA 方向以 2cm /s的速度向点 A 匀速运动,当点 M 到达点 B 时,两点同时停止运动,问:
(1)经过多长时间,MN的长为
(2)经过多长时间,△AMN 的面积等于矩形ABCD 面积的 ?
当堂测·夯基础
1.为了改善居民生活环境,云宁小区对一块矩形空地进行绿化,这块空地的长比宽多6米,面积为720平方米,设矩形空地的长为x 米,根据题意,所列方程正确的是 ( )
2.眉山市东坡区永丰村是“天府粮仓”示范区,该村的“智慧春耕”让生产更高效,提升了水稻亩产量,水稻亩产量从 2021年的 670 千克增长到了2023年的780 千克,该村水稻亩产量年平均增长率为x,则可列方程为 ( )
3.如图所示,在△ABC中,∠B=90°,AB=6 cm,BC=8cm ,点 P 从 A 点开始沿 AB 向 B 点以l cm/s的速度移动,点 Q 从 B 点开始沿BC 边向C 点以 2cm /s的速度移动.如果点 P,Q分别从A,B同时出发,当点 Q到达点 C 时,两点同时停止运动,那么 秒后,线段 PQ将△ABC分成面积1:2的两部分.
4.为增强学生身体素质,提高学生篮球运动竞技水平,扬州市开展“市长杯”篮球比赛,赛制为单循环形式(每两队之间赛一场).现计划赛程3天,每天安排5场比赛,则应邀请 个球队参赛.
5.在过去的 2023年,直播电商一词,我们并不陌生.原本以内容为主的视频平台在入局电商后,大力开拓直播带货模式,并实现高速增长.某电商对一款成本价为 40 元的小商品进行直播销售,如果按每件 60 元销售,每天可卖出 20 件.通过市场调查发现,每件小商品售价每降低 5元,日销售量增加10件.若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为 元.
6.一村民在 2021 年承包种植橙子树 200 亩,由于第一年收成不错,该村民每年都增加种植面积,到2023年,共种植288亩.
(1)求该村民这两年种植橙子亩数的年平均增长率;
(2)某水果批发店销售该种橙子,市场调查发现,当橙子售价为18 元/千克时,每天能售出 120 千克,售价每降低 2元,每天可多售出 30千克,为了减少库存,该店决定降价促销,已知该橙子的平均成本价为8元/千克,若使销售该种橙子每天获利840元,则售价应降低多少元
参考答案
【列清单·划重点】
知识点1 (2)等量关系 (3)未知数 (4)方程 (5)方程 (6)检验 (7)答
知识点2 3.售价一进价 单利润×数量
【明考点·识方法】
典例1
解:图1:设道路的宽为x米.依题意得(32-2x)(20-2x)=540,
整理得 即(x-1)(x-25)=0,
解得 (不合题意舍去).
答:道路宽为1米;
图2:设道路的宽为x米.依题意得(32-x)(20-x)=540,
整理得 即((x-2)(x-50)=0,
解得 (不合题意舍去).
答:道路宽为2米.
变式
解:(1)设矩形ABCD的边AB= xm,则边BC=70-2x+2=(72-2x)m.
根据题意,得x(72-2x)=640,化简,得
解得
当x=16时,72-2x=72-32=40(m),
当x=20时,72-2x=72-40=32(m).
答:当羊圈的长为40 m,宽为16 m或长为32m,宽为 20 m时,能围成一个面积为640 m 的羊圈;
(2)不能,
理由:由题意,得x(72-2x)=650,化简,得
∴一元二次方程没有实数根.
∴羊圈的面积不能达到 650 m .
典例2
解:(1)设该市改造老旧小区投入资金的年平均增长率为x,
依题意得1000(1+x) =1440,解得x =0.2=20%,x =-2.2(不符合题意,舍去).
答:该市改造老旧小区投入资金的年平均增长率为20%;
(2)设该市在 2024年可以改造 y个老旧小区,
依题意得 96×(1+50%)y≤1 440×(1+20%),解得 y≤12,
∴y的最大值为12.
答:该市在2024年最多可以改造12个老旧小区.
变式
解:(1)设2022年到 2024年这种药剂价格的年平均下降率为x,
根据题意得解得(不符合题意,舍去),
答:2022年到 2024年这种药剂价格的年平均下降率为30%;
(2)设此次价格的下降率是 y,
根据题意得196(1-y)≥147,解得 y≤0.25,∴y的最大值是0.25=25%.
答:此次价格的下降率最多是25%.
典例3
解:(1)方法1:设每千克特产应降价x元.根据题意,得
(60-x-40)(100+10x)=2240.
方法2:设每千克特产降价后定价为x元,
由题意,得(x-40)[100+10(60-x)]=2240,
故答案为:(60-x-40)(100+10x)=2 240,(x-40)[100+10(60-x)]=2 240;
(2)方法1:设每千克特产应降价x元.
根据题意,得(60-x-40)(100+10x)=2240,解得
要让销售量尽可能大,只能取x=6,60-6=54(元),
答:每千克特产应定价 54元.
方法2:设每千克特产降价后定价为x元,
由题意,得(x-40)[100+10(60-x)]=2240,解得
要让销售量尽可能大,只能取x=54,答:每千克特产应定价54元.
变式
解:(1)根据题意得 2=30+12=42(件),
∴平均每天销售数量为42件.
故答案为:42;
(2)设每件商品降价x元,则每件的销售利润为(40-x)元,平均每天的销售量为30+ 件,根据题意得(40-x)(30+4x)=2100,
整理得 解得
当x=10时,40-x=40-10=30>25,符合题意;
当 时: 不符合题意,舍去.
答:每件商品应降价 10元.
典例4
解:(1)根据题意得AP=2tcm,BQ=4tcm,所以 BP=(12-2t) cm,
故答案为:(12-2t);4t;
(2)如图,过点 D作DH⊥BC于点 H,
∵∠B=90°,即AB⊥BC.∴AB∥DH.
又∵D是AC的中点,DH是△ABC的中位线.
根据题意,得
整理,得t -6t+8=0.解得
即当 t = 2 或 4 时,△PDQ 的面 积是40 cm .
变式
解:(1)设经过 ts后,则 DN=2tcm,AN=(6 - 2t)cm, AM=tcm,MN的长为
根据题意,由勾股定理得AN +AM =MN ,即
解得
答:经过 2 s 或 s 之后,MN 的长为2 cm;
(2)设经过x秒,△AMN 的面积等于矩形ABCD 面积的
由题意得 DN=2x cm,AN=(6-2x) cm,AM= xcm,
∵矩形 ABCD中,AB=3cm,BC=6cm,
∴矩形 ABCD 的面积为AB·BC=3×6=18(cm ),
∴△AMN的面积
整理得 解得
答:经过1秒或2秒,△AMN的面积等于矩形ABCD面积的
【当堂测·夯基础】
1. A 2. B 3. 2或4 4. 6 5. 50
6.解:(1)设该村民这两年种植橙子亩数的年平均增长率为x,
根据题意,得
解得x =0.2=20%,x =-2.2(不符合题意,舍去).
答:该村民这两年种植橙子亩数的年平均增长率为20%;
(2)设售价应降价 y元,则每千克的销售利润为(18-y-8)元,每天能售出 千克,
根据题意,得 840,
整理得 解得y =6,y =-4(不符合题意,舍去).
答:售价应降低6元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
