高中数学人教A版(2019)必修二 第九章 统计测试卷(含答案)
文档属性
| 名称 | 高中数学人教A版(2019)必修二 第九章 统计测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 655.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-08 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
高中数学人教A版(2019)必修二 第九章 统计测试卷
一、单选题
1.(2023高一上·海淀期末)甲 乙两名学生,六次数学测验成绩(百分制)如图所示:
①甲同学成绩的中位数和极差都比乙同学大;
②甲同学的平均分比乙同学高;
③甲同学的成绩比乙同学稳定;
④甲同学成绩的方差大于乙同学成绩的方差.
上面说法正确的是( )
A.①③ B.①④ C.②④ D.②③
2.(2024高一下·柳州月考)某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名,现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
A.6 B.8 C.10 D.12
3.(2024高一下·十堰期末)有一组样本数据:5,6,6,6,7,7,8,8,9,9.则关于该组数据的下列数字特征中,数值最大的为( )
A.平均数 B.第50百分位数
C.极差 D.众数
4.对刻画数据的离散程度的量,下列说法正确的是( )
①应充分利用所得的数据,以便提供更确切的信息;②可以用多个数值来刻画数据的离散程度;③对于不同的数值,其离散程度大时,该数值应越小.
A.①和③ B.②和③ C.①和② D.都正确
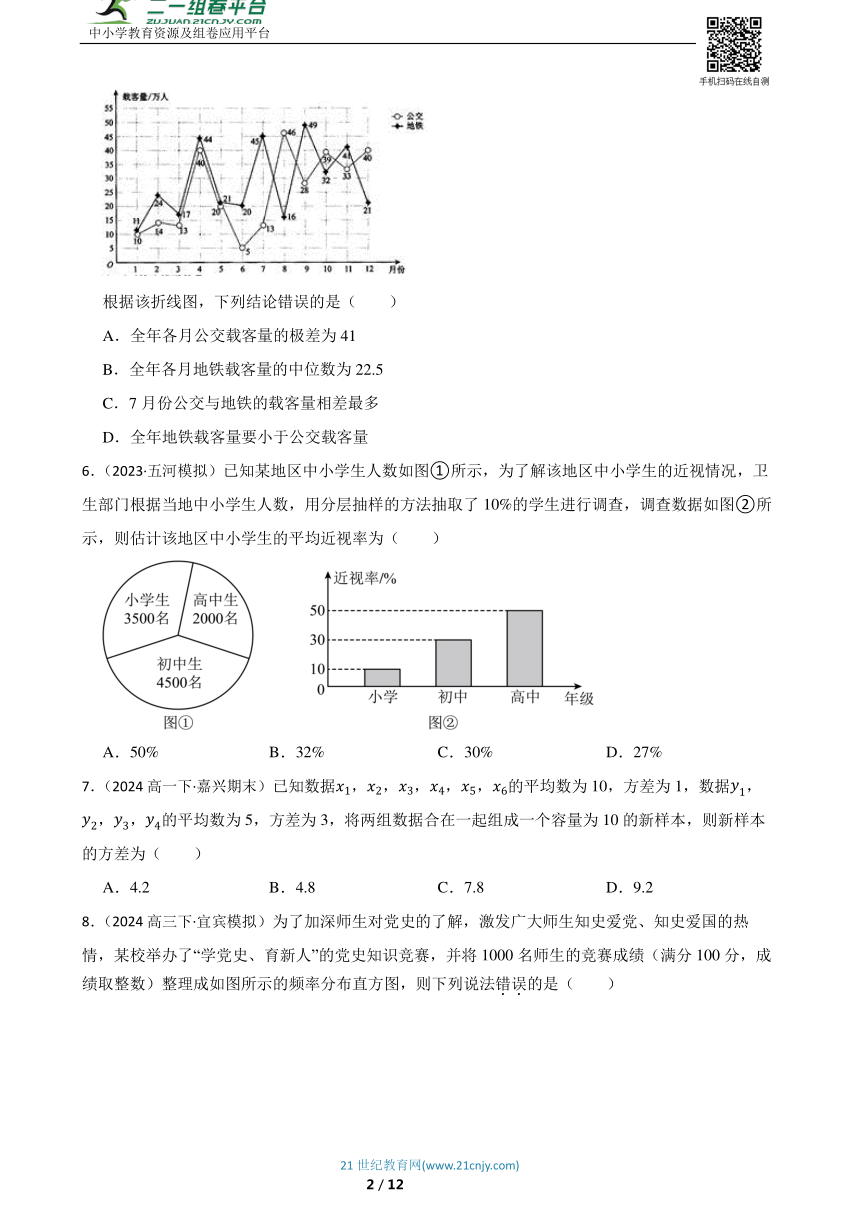
5.某城市为了了解市民搭乘公共交通工具的出行情况,收集并整理了2017年全年每月公交和地铁载客量的数据,绘制了下面的折线图:
根据该折线图,下列结论错误的是( )
A.全年各月公交载客量的极差为41
B.全年各月地铁载客量的中位数为22.5
C.7月份公交与地铁的载客量相差最多
D.全年地铁载客量要小于公交载客量
6.(2023·五河模拟)已知某地区中小学生人数如图①所示,为了解该地区中小学生的近视情况,卫生部门根据当地中小学生人数,用分层抽样的方法抽取了10%的学生进行调查,调查数据如图②所示,则估计该地区中小学生的平均近视率为( )
A.50% B.32% C.30% D.27%
7.(2024高一下·嘉兴期末)已知数据,,,,,的平均数为10,方差为1,数据,,,的平均数为5,方差为3,将两组数据合在一起组成一个容量为10的新样本,则新样本的方差为( )
A.4.2 B.4.8 C.7.8 D.9.2
8.(2024高三下·宜宾模拟)为了加深师生对党史的了解,激发广大师生知史爱党、知史爱国的热情,某校举办了“学党史、育新人”的党史知识竞赛,并将1000名师生的竞赛成绩(满分100分,成绩取整数)整理成如图所示的频率分布直方图,则下列说法错误的是( )
A.a的值为0.005
B.估计这组数据的众数为75分
C.估计成绩低于60分的有250人
D.估计这组数据的中位数为分
二、多选题
9.(2024高三下·金华模拟)从某小区抽取100户居民用户进行月用电量调查,发现他们的用电量都在之间,进行适当分组后(每组为左闭右开区间),画出频率分布直方图如图所示,记直方图中六个小矩形的面积从左到右依次为,则( )
A.x的值为0.0044
B.这100户居民该月用电量的中位数为175
C.用电量落在区间内的户数为75
D.这100户居民该月的平均用电量为
10.(2024高一下·温岭期中)已知互不相同的30个样本数据,若去掉其中最大和最小的数据,设剩下的28个样本数据的方差为,平均数为;去掉的两个数据的方差为,平均数为﹔原样本数据的方差为,平均数为,若=,则下列说法正确的是( )
A.
B.
C.剩下28个数据的中位数大于原样本数据的中位数
D.剩下28个数据的22%分位数不等于原样本数据的22%分位数
11.(2023高三上·东莞月考)“搜索指数”是网民通过搜索引擎,以搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民该关键词的搜索次数越多,对与该关键词相关的信息关注度也越高.如图是2018年9月到2019年2月这半年中,某个关键词的搜索指数变化的走势图.
根据该走势图,下列结论正确的是( )
A.这半年中,网民对与该关键词相关的信息关注度呈周期性变化
B.这半年中,网民对与该关键词相关的信息关注度不断减弱
C.从网民对该关键词的搜索指数来看,2018年10月份的方差大于11月份的方差
D.从网民对该关键词的搜索指数来看,2018年12月份的平均值大于2019年1月份的平均值
12.(2023高三上·长春期中)下列说法正确的是( )
A.一组数1,5,6,7,10,13,15,16,18,20的第75百分位数为16
B.在经验回归方程中,当解释变量每增加1个单位时,相应变量增加个单位
C.数据的方差为,则数据的方差为
D.一个样本的方差,则这组样本数据的总和等于100
三、填空题
13.(2024高二上·云南月考)小洪从某公司购进6袋白糖,每袋白糖的标准质量是500g,为了了解这些白糖的质量情况,称出各袋白糖的质量(单位:g)为495,500,500,495,510,500,则这6袋白糖的平均质量为 g,这6袋白糖质量的标准差为 g.
14.(2024高三上·广东会考)三个人过关,甲带元,乙带元,丙带元,共要交100元关税,若按照比例缴纳,乙应交 元.(结果保留整数)
15.(2024高一下·平湖月考)常言道:国以民为本,民以食为天.食品安全问题是人类生存的第一需要.学校为了解学生对食堂满意情况组织了一次座谈会,并利用分层抽样的方法从高中3个年级中随机抽取了150人参加,其中高一、高二年级各抽取了40人,50人,若高三年级有学生1200人,则该高中共有学生 人.
16.(2023高一上·延庆期末)某单位共有20人,他们的年龄分布如下表所示.
年龄 28 29 30 32 36 40 45
人数 2 2 3 6 4 2 1
则这20人年龄的众数是 ,75%分位数是 .
四、解答题
17.(2023高三下·杭州模拟)为保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设某高校为了解全校学生的阅读情况,随机调查了200名学生的每周阅读时间x(单位:小时)并绘制如图所示的频率分布直方图:
(1)求这200名学生每周阅读时间的样本平均数和样本方差(同一组的数据用该组区间中点值代表);
(2)由直方图可以看出,目前该校学生每周的阅读时间x大致服从正态分布,其中近似为样本平均数,近似为样本方差.
①一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若,令,则,且利用直方图得到的正态分布,求;
②从该高校的学生中随机抽取20名,记Z表示这20名学生中每周阅读时间超过10小时的人数,求Z的均值.
参考数据:,若,则.
18.(2024高二上·柳河月考)某县共有90个农村淘宝服务网点,随机抽取其中的6个网点统计其元旦期间的网购金额(单位:万元),相关数据如下表所示:
网点 1 2 3 4 5 6
金额 6 4 12 18 12 20
(1)计算样本数据的平均数;
(2)若将网购金额(单位:万元)不小于18的服务网点定义为优秀服务网点,其余为非优秀服务网点,试估计这90个服务网点中优秀服务网点的个数;
(3)从随机抽取的6个服务网点中任取2个进行网购商品的调查,求恰有1个网点是优秀服务网点的概率.
19.(2024高二下·大理期中) 某校为了提高学生安全意识,利用自习课时间开展“防溺水”安全知识竞赛(满分150分),加强对学生的安全教育,通过知识竞赛的形式,不仅帮助同学们发现自己对“防溺水”知识认知的不足之处,还教会了同学们溺水自救的方法,提高了应急脱险能力.现抽取了甲组20名同学的成绩记录如下:甲:92,96,99,103,104,105,113,114,117,117,121,123,124,126,129,132,134,136,141,142.抽取了乙组20名同学的成绩,将成绩分成[100,110),[110,120),[120,130),[130,140),[140,150]五组,并画出了其频率分布直方图.
(1)根据以上记录数据求甲组20名同学成绩的中位数和第80百分位数;
(2)估计乙组20名同学成绩的平均分(同组中的每个数据用该组区间的中点值代表替);
(3)现从甲乙两组同学的不低于140分的成绩中任意取出2个人的成绩,求取出的2个人的成绩不在同一组的概率.
20.(2024高一下·河北期末)我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照,,…,分成9组,制成了如图所示的频率分布直方图.
(1)求频率分布直方图中a的值;
(2)已知该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由;
(3)估计居民月均用水量的众数、中位数,说明理由.
21.(2024高二上·柳州期中)世界杯足球赛备受瞩目,一时间掀起了国内外的足球热潮,某机构为了解球迷对足球的喜爱,为此进行了调查.现从球迷中随机选出人作为样本,并将这人按年龄分组:第组,第组,第组,第组,第组,得到频率分布直方图如图所示.
(1)估计样本数据的上四分位数(也称第三四分位数,第百分位数)
(2)若将频率视为概率,现在要从和两组中用分层抽样的方法抽取人,再从这人中随机抽取人进行座谈,求抽取的人中至少有人的年龄在组的概率.
22.(2024高一下·金东期中)某学校1000名学生参加信息技术学分认定考试,用按性别比例分层随机抽样的方法从中抽取了100名学生的成绩,记录他们的分数,并将数据分成8组:,,整理得到如下频率分布直方图:
(1)求图中的值,并估计全校学生中成绩不低于70分的学生人数;
(2)已知样本中分数不低于70的男生占样本中全部男生人数的,且样本中分数不低于70的男生与女生人数之比为,求总体中男生人数和女生人数之比;
(3)估计该校1000名学生成绩的平均值.
答案解析部分
1.【答案】B
【知识点】茎叶图;众数、中位数、平均数;极差、方差与标准差
2.【答案】B
【知识点】分层抽样方法
3.【答案】A
【知识点】众数、中位数、平均数;极差、方差与标准差;用样本估计总体的百分位数
4.【答案】C
【知识点】众数、中位数、平均数;极差、方差与标准差
5.【答案】D
【知识点】频率分布折线图、密度曲线;众数、中位数、平均数;极差、方差与标准差
6.【答案】D
【知识点】分层抽样方法;众数、中位数、平均数
7.【答案】C
【知识点】分层抽样方法;众数、中位数、平均数;极差、方差与标准差
8.【答案】D
【知识点】众数、中位数、平均数;概率的基本性质
9.【答案】A,D
【知识点】频率分布直方图;众数、中位数、平均数
10.【答案】A,B,D
【知识点】众数、中位数、平均数;极差、方差与标准差;用样本估计总体的百分位数
11.【答案】C,D
【知识点】频率分布折线图、密度曲线;众数、中位数、平均数;极差、方差与标准差
12.【答案】A,C,D
【知识点】简单随机抽样;众数、中位数、平均数;极差、方差与标准差;用样本的频率分布估计总体分布;离散型随机变量及其分布列;离散型随机变量的期望与方差
13.【答案】500;5
【知识点】众数、中位数、平均数;极差、方差与标准差
14.【答案】32
【知识点】分层抽样方法
15.【答案】
【知识点】分层抽样方法
16.【答案】32;36
【知识点】众数、中位数、平均数;用样本的数字特征估计总体的数字特征
17.【答案】(1)解:根据频率分布直方图知,阅读时间在区间
内的频率分别为,
,
,
所以样本平均数和样本方差分别为9,1.78.
(2)解:①由题意知,,则有,
,,
②由①知,可得,
所以Z的均值.
【知识点】众数、中位数、平均数;极差、方差与标准差;离散型随机变量的期望与方差;正态密度曲线的特点;概率的应用
18.【答案】(1)12
(2)30(个)
(3).
【知识点】简单随机抽样;古典概型及其概率计算公式
19.【答案】(1)解:由题意可知,甲组20名同学成绩的中位数是,
因为,所以甲组20名同学成绩的第80百分位数为.
所以甲组20名同学成绩的中位数为119, 甲组20名同学成绩的第80百分位数为133.
(2)解:由频率分布直方图可知:乙组20名同学成绩的平均数分为:
.
(3)解:甲组20名同学的成绩不低于140(分)的有2个,记作、;
乙组20名同学的成绩不低于140(分)的有个,记作、、.
记事件为“取出的2个成绩不是同一组”,任意选出2个成绩的所有样本点为:,,,,,,,,,,共10个,其中两个成绩不是同一组的样本点是:,,,,,,共6个,
故.
所以取出的2个人的成绩不在同一组的概率为.
【知识点】频率分布直方图;众数、中位数、平均数;古典概型及其概率计算公式;用样本估计总体的百分位数
20.【答案】(1)解:因为由频率分布直方图知,,解得,
所以直方图中的值为;
(2)解:因为由图得月均用水量不低于3吨的频率为,
所以估计全市居民中月均用水量不低于3吨的人数为(人);
(3)解:(3)由图可知,众数是;
因为,
,
所以中位数在区间内,设为,
则,解得,
即中位数为.
【知识点】频率分布直方图;众数、中位数、平均数
21.【答案】(1)
(2)
【知识点】分层抽样方法;频率分布直方图;古典概型及其概率计算公式;用样本估计总体的百分位数
22.【答案】(1)解:由频率分布直方图中每个小矩形的面积之和为1,
可得,解得;
样本中成绩不低于70分的频率为,
则全校学生中成绩不低于70分的学生人数为;
(2)解:由题意可知,样本中分数不低于70的学生人数为,则样本中分数不低于70的男生人数为,
因为样本中分数不低于70的男生占样本中全部男生人数的,所以样本中全部男生人数为60,女生人数为,
所以样本中男生人数与女生人数之比为,即总体中男生和女生人数之比为;
(3)解:估计该校1000名学生成绩的平均值为
.
【知识点】频率分布直方图;众数、中位数、平均数;用样本的频率分布估计总体分布
21世纪教育网(www.21cnjy.com)
2 / 12
高中数学人教A版(2019)必修二 第九章 统计测试卷
一、单选题
1.(2023高一上·海淀期末)甲 乙两名学生,六次数学测验成绩(百分制)如图所示:
①甲同学成绩的中位数和极差都比乙同学大;
②甲同学的平均分比乙同学高;
③甲同学的成绩比乙同学稳定;
④甲同学成绩的方差大于乙同学成绩的方差.
上面说法正确的是( )
A.①③ B.①④ C.②④ D.②③
2.(2024高一下·柳州月考)某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名,现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
A.6 B.8 C.10 D.12
3.(2024高一下·十堰期末)有一组样本数据:5,6,6,6,7,7,8,8,9,9.则关于该组数据的下列数字特征中,数值最大的为( )
A.平均数 B.第50百分位数
C.极差 D.众数
4.对刻画数据的离散程度的量,下列说法正确的是( )
①应充分利用所得的数据,以便提供更确切的信息;②可以用多个数值来刻画数据的离散程度;③对于不同的数值,其离散程度大时,该数值应越小.
A.①和③ B.②和③ C.①和② D.都正确
5.某城市为了了解市民搭乘公共交通工具的出行情况,收集并整理了2017年全年每月公交和地铁载客量的数据,绘制了下面的折线图:
根据该折线图,下列结论错误的是( )
A.全年各月公交载客量的极差为41
B.全年各月地铁载客量的中位数为22.5
C.7月份公交与地铁的载客量相差最多
D.全年地铁载客量要小于公交载客量
6.(2023·五河模拟)已知某地区中小学生人数如图①所示,为了解该地区中小学生的近视情况,卫生部门根据当地中小学生人数,用分层抽样的方法抽取了10%的学生进行调查,调查数据如图②所示,则估计该地区中小学生的平均近视率为( )
A.50% B.32% C.30% D.27%
7.(2024高一下·嘉兴期末)已知数据,,,,,的平均数为10,方差为1,数据,,,的平均数为5,方差为3,将两组数据合在一起组成一个容量为10的新样本,则新样本的方差为( )
A.4.2 B.4.8 C.7.8 D.9.2
8.(2024高三下·宜宾模拟)为了加深师生对党史的了解,激发广大师生知史爱党、知史爱国的热情,某校举办了“学党史、育新人”的党史知识竞赛,并将1000名师生的竞赛成绩(满分100分,成绩取整数)整理成如图所示的频率分布直方图,则下列说法错误的是( )
A.a的值为0.005
B.估计这组数据的众数为75分
C.估计成绩低于60分的有250人
D.估计这组数据的中位数为分
二、多选题
9.(2024高三下·金华模拟)从某小区抽取100户居民用户进行月用电量调查,发现他们的用电量都在之间,进行适当分组后(每组为左闭右开区间),画出频率分布直方图如图所示,记直方图中六个小矩形的面积从左到右依次为,则( )
A.x的值为0.0044
B.这100户居民该月用电量的中位数为175
C.用电量落在区间内的户数为75
D.这100户居民该月的平均用电量为
10.(2024高一下·温岭期中)已知互不相同的30个样本数据,若去掉其中最大和最小的数据,设剩下的28个样本数据的方差为,平均数为;去掉的两个数据的方差为,平均数为﹔原样本数据的方差为,平均数为,若=,则下列说法正确的是( )
A.
B.
C.剩下28个数据的中位数大于原样本数据的中位数
D.剩下28个数据的22%分位数不等于原样本数据的22%分位数
11.(2023高三上·东莞月考)“搜索指数”是网民通过搜索引擎,以搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民该关键词的搜索次数越多,对与该关键词相关的信息关注度也越高.如图是2018年9月到2019年2月这半年中,某个关键词的搜索指数变化的走势图.
根据该走势图,下列结论正确的是( )
A.这半年中,网民对与该关键词相关的信息关注度呈周期性变化
B.这半年中,网民对与该关键词相关的信息关注度不断减弱
C.从网民对该关键词的搜索指数来看,2018年10月份的方差大于11月份的方差
D.从网民对该关键词的搜索指数来看,2018年12月份的平均值大于2019年1月份的平均值
12.(2023高三上·长春期中)下列说法正确的是( )
A.一组数1,5,6,7,10,13,15,16,18,20的第75百分位数为16
B.在经验回归方程中,当解释变量每增加1个单位时,相应变量增加个单位
C.数据的方差为,则数据的方差为
D.一个样本的方差,则这组样本数据的总和等于100
三、填空题
13.(2024高二上·云南月考)小洪从某公司购进6袋白糖,每袋白糖的标准质量是500g,为了了解这些白糖的质量情况,称出各袋白糖的质量(单位:g)为495,500,500,495,510,500,则这6袋白糖的平均质量为 g,这6袋白糖质量的标准差为 g.
14.(2024高三上·广东会考)三个人过关,甲带元,乙带元,丙带元,共要交100元关税,若按照比例缴纳,乙应交 元.(结果保留整数)
15.(2024高一下·平湖月考)常言道:国以民为本,民以食为天.食品安全问题是人类生存的第一需要.学校为了解学生对食堂满意情况组织了一次座谈会,并利用分层抽样的方法从高中3个年级中随机抽取了150人参加,其中高一、高二年级各抽取了40人,50人,若高三年级有学生1200人,则该高中共有学生 人.
16.(2023高一上·延庆期末)某单位共有20人,他们的年龄分布如下表所示.
年龄 28 29 30 32 36 40 45
人数 2 2 3 6 4 2 1
则这20人年龄的众数是 ,75%分位数是 .
四、解答题
17.(2023高三下·杭州模拟)为保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设某高校为了解全校学生的阅读情况,随机调查了200名学生的每周阅读时间x(单位:小时)并绘制如图所示的频率分布直方图:
(1)求这200名学生每周阅读时间的样本平均数和样本方差(同一组的数据用该组区间中点值代表);
(2)由直方图可以看出,目前该校学生每周的阅读时间x大致服从正态分布,其中近似为样本平均数,近似为样本方差.
①一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若,令,则,且利用直方图得到的正态分布,求;
②从该高校的学生中随机抽取20名,记Z表示这20名学生中每周阅读时间超过10小时的人数,求Z的均值.
参考数据:,若,则.
18.(2024高二上·柳河月考)某县共有90个农村淘宝服务网点,随机抽取其中的6个网点统计其元旦期间的网购金额(单位:万元),相关数据如下表所示:
网点 1 2 3 4 5 6
金额 6 4 12 18 12 20
(1)计算样本数据的平均数;
(2)若将网购金额(单位:万元)不小于18的服务网点定义为优秀服务网点,其余为非优秀服务网点,试估计这90个服务网点中优秀服务网点的个数;
(3)从随机抽取的6个服务网点中任取2个进行网购商品的调查,求恰有1个网点是优秀服务网点的概率.
19.(2024高二下·大理期中) 某校为了提高学生安全意识,利用自习课时间开展“防溺水”安全知识竞赛(满分150分),加强对学生的安全教育,通过知识竞赛的形式,不仅帮助同学们发现自己对“防溺水”知识认知的不足之处,还教会了同学们溺水自救的方法,提高了应急脱险能力.现抽取了甲组20名同学的成绩记录如下:甲:92,96,99,103,104,105,113,114,117,117,121,123,124,126,129,132,134,136,141,142.抽取了乙组20名同学的成绩,将成绩分成[100,110),[110,120),[120,130),[130,140),[140,150]五组,并画出了其频率分布直方图.
(1)根据以上记录数据求甲组20名同学成绩的中位数和第80百分位数;
(2)估计乙组20名同学成绩的平均分(同组中的每个数据用该组区间的中点值代表替);
(3)现从甲乙两组同学的不低于140分的成绩中任意取出2个人的成绩,求取出的2个人的成绩不在同一组的概率.
20.(2024高一下·河北期末)我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照,,…,分成9组,制成了如图所示的频率分布直方图.
(1)求频率分布直方图中a的值;
(2)已知该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由;
(3)估计居民月均用水量的众数、中位数,说明理由.
21.(2024高二上·柳州期中)世界杯足球赛备受瞩目,一时间掀起了国内外的足球热潮,某机构为了解球迷对足球的喜爱,为此进行了调查.现从球迷中随机选出人作为样本,并将这人按年龄分组:第组,第组,第组,第组,第组,得到频率分布直方图如图所示.
(1)估计样本数据的上四分位数(也称第三四分位数,第百分位数)
(2)若将频率视为概率,现在要从和两组中用分层抽样的方法抽取人,再从这人中随机抽取人进行座谈,求抽取的人中至少有人的年龄在组的概率.
22.(2024高一下·金东期中)某学校1000名学生参加信息技术学分认定考试,用按性别比例分层随机抽样的方法从中抽取了100名学生的成绩,记录他们的分数,并将数据分成8组:,,整理得到如下频率分布直方图:
(1)求图中的值,并估计全校学生中成绩不低于70分的学生人数;
(2)已知样本中分数不低于70的男生占样本中全部男生人数的,且样本中分数不低于70的男生与女生人数之比为,求总体中男生人数和女生人数之比;
(3)估计该校1000名学生成绩的平均值.
答案解析部分
1.【答案】B
【知识点】茎叶图;众数、中位数、平均数;极差、方差与标准差
2.【答案】B
【知识点】分层抽样方法
3.【答案】A
【知识点】众数、中位数、平均数;极差、方差与标准差;用样本估计总体的百分位数
4.【答案】C
【知识点】众数、中位数、平均数;极差、方差与标准差
5.【答案】D
【知识点】频率分布折线图、密度曲线;众数、中位数、平均数;极差、方差与标准差
6.【答案】D
【知识点】分层抽样方法;众数、中位数、平均数
7.【答案】C
【知识点】分层抽样方法;众数、中位数、平均数;极差、方差与标准差
8.【答案】D
【知识点】众数、中位数、平均数;概率的基本性质
9.【答案】A,D
【知识点】频率分布直方图;众数、中位数、平均数
10.【答案】A,B,D
【知识点】众数、中位数、平均数;极差、方差与标准差;用样本估计总体的百分位数
11.【答案】C,D
【知识点】频率分布折线图、密度曲线;众数、中位数、平均数;极差、方差与标准差
12.【答案】A,C,D
【知识点】简单随机抽样;众数、中位数、平均数;极差、方差与标准差;用样本的频率分布估计总体分布;离散型随机变量及其分布列;离散型随机变量的期望与方差
13.【答案】500;5
【知识点】众数、中位数、平均数;极差、方差与标准差
14.【答案】32
【知识点】分层抽样方法
15.【答案】
【知识点】分层抽样方法
16.【答案】32;36
【知识点】众数、中位数、平均数;用样本的数字特征估计总体的数字特征
17.【答案】(1)解:根据频率分布直方图知,阅读时间在区间
内的频率分别为,
,
,
所以样本平均数和样本方差分别为9,1.78.
(2)解:①由题意知,,则有,
,,
②由①知,可得,
所以Z的均值.
【知识点】众数、中位数、平均数;极差、方差与标准差;离散型随机变量的期望与方差;正态密度曲线的特点;概率的应用
18.【答案】(1)12
(2)30(个)
(3).
【知识点】简单随机抽样;古典概型及其概率计算公式
19.【答案】(1)解:由题意可知,甲组20名同学成绩的中位数是,
因为,所以甲组20名同学成绩的第80百分位数为.
所以甲组20名同学成绩的中位数为119, 甲组20名同学成绩的第80百分位数为133.
(2)解:由频率分布直方图可知:乙组20名同学成绩的平均数分为:
.
(3)解:甲组20名同学的成绩不低于140(分)的有2个,记作、;
乙组20名同学的成绩不低于140(分)的有个,记作、、.
记事件为“取出的2个成绩不是同一组”,任意选出2个成绩的所有样本点为:,,,,,,,,,,共10个,其中两个成绩不是同一组的样本点是:,,,,,,共6个,
故.
所以取出的2个人的成绩不在同一组的概率为.
【知识点】频率分布直方图;众数、中位数、平均数;古典概型及其概率计算公式;用样本估计总体的百分位数
20.【答案】(1)解:因为由频率分布直方图知,,解得,
所以直方图中的值为;
(2)解:因为由图得月均用水量不低于3吨的频率为,
所以估计全市居民中月均用水量不低于3吨的人数为(人);
(3)解:(3)由图可知,众数是;
因为,
,
所以中位数在区间内,设为,
则,解得,
即中位数为.
【知识点】频率分布直方图;众数、中位数、平均数
21.【答案】(1)
(2)
【知识点】分层抽样方法;频率分布直方图;古典概型及其概率计算公式;用样本估计总体的百分位数
22.【答案】(1)解:由频率分布直方图中每个小矩形的面积之和为1,
可得,解得;
样本中成绩不低于70分的频率为,
则全校学生中成绩不低于70分的学生人数为;
(2)解:由题意可知,样本中分数不低于70的学生人数为,则样本中分数不低于70的男生人数为,
因为样本中分数不低于70的男生占样本中全部男生人数的,所以样本中全部男生人数为60,女生人数为,
所以样本中男生人数与女生人数之比为,即总体中男生和女生人数之比为;
(3)解:估计该校1000名学生成绩的平均值为
.
【知识点】频率分布直方图;众数、中位数、平均数;用样本的频率分布估计总体分布
21世纪教育网(www.21cnjy.com)
2 / 12
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
