八年级北师大版拼图与勾股定理说课

课件34张PPT。《拼图与勾股定理》说课教师：临泽县板桥中学顾政教 材：北师大出版社新世纪版数学(八年级上册)一、教材分析二、教法选择三、学法指导四、课程设计五、相关说明课题:拼图与勾股定理一、教材分析1、教材的地位和作用 勾股定理有着悠久的历史，是人类最伟大的数学发现之一。但由于教材的编写遵循了简约性原则，在学习勾股定理知识的过程中，没能更深入地介绍它产生、发展的历史背景、多样的验证方法，以及在人类文化发展史上的贡献。
因此，在学生完成了《勾股定理》这章的学习之后，设置了《拼图与勾股定理》的课题学习，它属于《数学课程标准》中所规定的“实践与综合应用”领域的内容，是对课本知识进一步的延伸和拓展，让学生更全面的认识勾股定理，了解拼图与定理证明之间的内在联系，通过经历综合应用知识解决问题的过程，领会其中的数学思想方法，以开拓学生视野，激发他们的创新意识和学习数学的兴趣。
一、教材分析2、教学目标<1> 通过对几种常见的勾股定理验证方法，进行分析和欣赏。理解数 学知识之间的内在联系，体会数形结合的思想方法，进一步感悟勾股定理的文化价值。<２> 通过拼图活动，尝试验证勾股定理，培养学生的动手实践和创新能力。 <３>让学生经历查询资料、自主探究、合作交流、观察比较、计算推理、动手操作等过程，获得一些研究问题的方法，取得成功和克服困难的经验，培养学生良好的思维品质，增进他们数学学习的信心。 3、教学重点和难点难点：重点：<1> 分析和欣赏几种常见的验证勾股定理的方法。<2> 尝试利用“五巧板”拼图，验证勾股定理。<1> “数形结合”思想方法的理解和应用。<2> 通过拼图，探求验证勾股定理的新方法。二、教法选择“操作＋思考”的方式符合八年级学生认知水平，适应其思维发展规律及心理特征。在学法上，充分发挥学生在教学中的主体作用，采取让学生动手实践，合作探究的方式进行学习。三、学法指导在学法上，充分发挥学生在教学中的主体作用，采取让学生通过动手实践，合作探究的方式进行学习。“操作＋思考”的方式符合八年级学生认知水平，适应其思维发展规律及心理特征。四、课程设计验证方法的
收集与整理探究成果的
交流与展示小结反思，
课题拓展文化价值的
了解与探讨尝试拼图，
验证定理验证过程的
分析与欣赏1．课前自主探究活动《勾股定理证明方法汇总》 1．课前自主探究活动探究报告具体的做法是：
请各个学习小组从网络或书籍上，尽可能多的寻找和了解验证勾股定理的方法。
2． 探 究 成 果 的

交 流 与 展 示
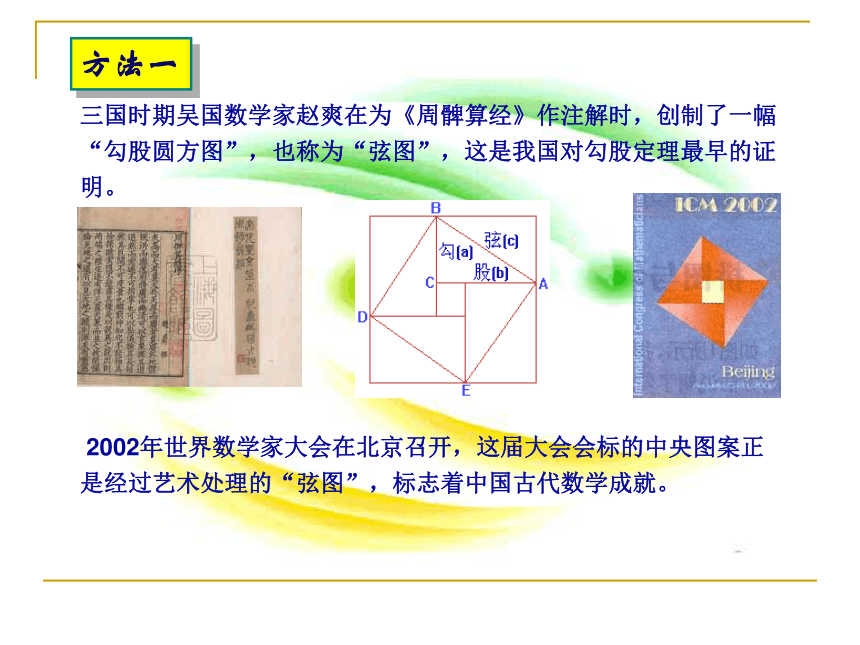
三国时期吴国数学家赵爽在为《周髀算经》作注解时，创制了一幅“勾股圆方图”，也称为“弦图”，这是我国对勾股定理最早的证明。 2002年世界数学家大会在北京召开，这届大会会标的中央图案正是经过艺术处理的“弦图”，标志着中国古代数学成就。 方法一约公元 263 年，三国时代魏国的数学家刘徽为古籍《九章算术》作注释时，用“出入相补法”证明了勾股定理。 方法二希腊数学家欧几里得（Euclid，公元前330～公元前275）在巨著《几何原本》给出一个公理化的证明。 1955年希腊为了纪念二千五百年前古希腊在勾股定理上的贡献，发行了一张邮票，图案是由三个棋盘排列而成。 方法三其它方法<4> 美国第二十任总统伽菲尔德的证法，被称为“总统证法”。 如图，梯形由三个直角三角形组合而成，利用面积公式，列出代数关系式得：化简为：<5>意大利著名画家达·芬奇的证法： <6> 在印度、在阿拉伯世界和欧洲出现的一种拼图证明。 做法是将一条垂直线和一条水平线，将较大直角边的正方形分成 4 分。之后依照图七中的颜色，将两个直角边的正方形填入斜边正方形之中，便可完成定理的证明<7> 据传是当年毕达哥拉斯发现勾股定理时做出的证明。 将4个全等的直角三角形拼成边长为(a＋b)的正方形ABCD，使中间留下边长c的一个正方形洞．画出正方形ABCD．移动三角形至图2所示的位置中，于是留下了边长分别为a与b的两个正方形洞．则图1和图2中的白色部分面积必定相等，所以c2=a2+b2图1图23．验证过程的分析与欣赏 问题思考 这些验证方法，有什么共同点和
不同点？
cb ? a三种类型：用几何图形的截、割、拼、补，来证明代数式之间的恒等关系。体现了以形证数、形数统一、代数和几何的紧密结合 。第一种类型：以赵爽的“弦图”为代表美国第二十任总统伽菲尔德的证法，被称为“总统证法”。 如图，梯形由三个直角三角形组合而成，利用面积公式，列出代数关系式得：化简为：意大利著名画家达·芬奇的证法： 据传是当年毕达哥拉斯发现勾股定理时做出的证明。 将4个全等的直角三角形拼成边长为(a＋b)
的正方形ABCD，使中间留下边长c的一个正方
形洞．画出正方形ABCD．移动三角形至图2所
示的位置中，于是留下了边长分别为a与b的两
个正方形洞．则图1和图2中的白色部分面积必
定相等，所以c2=a2+b2图1图2第二种类型：以刘徽的“青朱出入图”为代表，证明不需用任何数学符号和文字，更不需进行运算，隐含在图中的勾股定理便清晰地呈现，整个证明单靠移动几块图形而得出，被称为“无字证明”。 在印度、在阿拉伯世界和欧洲出现的一种拼图证明。 做法是将一条垂直线和一条水平线，将较大直角边的正方形分成 4 分。之后依照图中的颜色，将两个直角边的正方形填入斜边正方形之中，便可完成定理的证明。第三种类型：以欧几里得的证明方法为代表，运用欧氏几何的基本定理进行证明，反映了勾股定理的几何意义。如图，过 A 点画一直线 AL 使其垂直于 DE， 并交 DE 于 L，交 BC 于 M。通过证明△BCF≌△BDA，利用三角形面积与长方形面积的关系，得到正方形ABFG与矩形BDLM等积，同理正方形ACKH与 矩形MLEC也等积，于是推得。 以上的证明方法都从几何图形的面积变化入手，运用了数形结合的思想方法，其中第一、二种类型还与拼图有着密切的关系。 4.勾股定理的文化价值(1) 勾股定理是联系数学中数与形的第一定理。(2) 勾股定理反映了自然界基本规律,有文明的宇宙“人”都应该认识它，因而勾股定理图被建议作为与“外星人”联系的信号。(3)勾股定理导致不可通约量的发现，引发第一次数学危机。(4)勾股定理公式是第一个不定方程，为不定方程的解题程序树立了一个范式。5.尝试拼图，验证勾股定理abcabc6.小结反思,课题拓展我最大的收获；我表现较好的方面；我学会了哪些知识；我还有哪些疑惑……学生反思：（1）写数学日记并发挥你的聪明才智，去探索勾股定理、去研究勾股定理，你又有什么新的发现？
（2）尝试用七巧板拼图，你能验证勾股定理吗？
课题拓展：评价表板书设计 1、拼图验证勾股定理的一些方法展示 课题：拼图与勾股定理2、勾股定理的文化价值3、利用“五巧板”拼图验证勾股定理学生拼图作品
展示台： 时间安排 验证方法展示、分析与欣赏大约20分钟勾股定理文化价值的探讨大约4分钟利用“五巧板”拼图验证勾股定理大约16分钟小结反思，课题拓展大约5分钟