高中数学人教A版(2019)选修三第八章 成对数据的统计分布(含答案)
文档属性
| 名称 | 高中数学人教A版(2019)选修三第八章 成对数据的统计分布(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 217.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-08 14:12:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
高中数学人教A版(2019)选修三第八章 成对数据的统计分布
一、单选题
1.(2018高一下·河南月考)已知 是两个变量,下列四个散点图中, 呈正相关趋势的是( )
A. B.
C. D.
2.(2020高二下·阳江月考)某市政府调查市民收入与旅游愿望时,采用独立检验法抽取3000人,计算发现 ,则根据这一数据查阅下表,市政府断言市民收入增减与旅游愿望有关系的可信程度是( )
… 0.15 0.10 0.05 0.025 0.010 0.005 0.001
… 2.072 2.706 3.841 5.024 6.635 7.879 10.828
A.95% B.97.5% C.99.5% D.99.9%
3.(2024高二下·通化期中)要判断成对数据的线性相关程度的强弱,可以通过比较它们的样本相关系数r的大小,以下是四组数据的相关系数的值,则线性相关最强的是( )
A. B. C. D.
4.(2018高二下·黑龙江期中)在对具有线性相关的两个变量 和 进行统计分析时,得到如下数据:
4 8 10 12
1 2 3 5 6
由表中数据求得 关于 的回归方程为 ,则 , , 这三个样本点中落在回归直线下方的有( )个
A.1 B.2 C.3 D.0
5.(2021高二下·肇庆期末)某学校学生服务中心为了解在校学生对学校后勤工作的满意度﹐随机调查了200名学生,其中男女生比例为3:2并对这些学生进行了问卷调查,学生对后勤工作给出了满意或不满意的总体评价﹐得到下面的2×2列联表:
满意 不满意 总计
男生 104
女生 24
总计 200
附: ,其中 .
P(K2≥k0) 0.10 0.05 0.025 0.010 0.005 0.001
k0 2.706 3.841 5.024 6.635 7.879 10.828
则下列说法正确的是( )
A.2×2列联表中男生不满意的人数为18
B.2×2列联表中女生满意的人数为54
C.没有99.5%的把握认为男生与女生对后勤工作的评价有差异
D.有99.5%的把握认为男生与女生对后勤工作的评价有差异
6.(2017高二下·沈阳期末)四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程和相关系数r,分别得到以下四个结论:
①②
③④
其中,一定不正确的结论序号是( )
A.②③ B.①④ C.①②③ D.②③④
7.一台机器由于使用时间较长,但还可以使用,它按不同的转速生产出来的某机器零件有一些会有缺点,每小时生产有缺点零件的多少随机器运转的速度而变化,如表是抽样试验结果:
转速x/(rad/s) 16 14 12 8
每小时生产有缺点的零件数y/件 11 9 8 5
若实际生产中,允许每小时的产品中有缺点的零件数最多为10个,那么机器的转速应该控制所在的范围是( )
A.10转/s以下 B.15转/s以下
C.20转/s以下 D.25转/s以下
8.(2016·德州模拟)为了增强环保意识,某校从男生中随机制取了60人,从女生中随机制取了50人参加环保知识测试,统计数据如下表所示:
优秀 非优秀 总计
男生 40 20 60
女生 20 30 50
总计 60 50 110
附:x2=
P(K2≥k) 0.500 0.100 0.050 0.010 0.001
k 0.455 2.706 3.841 6.635 10.828
则有( )的把握认为环保知识是否优秀与性别有关.
A.90% B.95% C.99% D.99.9%
9.(2016高二上·鹤岗期中)某公司为确定明年投入某产品的广告支出,对近5年的广告支出m与销售额y(单位:百万元)进行了初步统计,得到下列表格中的数据:
y 30 40 p 50 70
m 2 4 5 6 8
经测算,年广告支出m与年销售额y满足线性回归方程 =6.5m+17.5,则p的值为( )
A.45 B.50 C.55 D.60
10.下表是某厂1~4月份用水量(单位:百吨)的一组数据:
月份x 1 2 3 4
用水量y 4.5 4 3 2.5
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是y=-0.7x+a,则a等于( )
A.10.5 B.5.15 C.5.2 D.5.25
二、多选题
11.(2022高三上·珠海期末)以下结论正确的是( )
A.两个随机变量的线性相关性越强,则相关系数r的绝对值越接近于1
B.在检验A与B是否有关的过程中,根据数据算得的值,越小,认为“A与B有关”的把握越小
C.随机变量,若,,则
D.在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合效果越好
12.(2022·湖北模拟)如图,5个数据,去掉点后,下列说法正确的是( )
A.相关系数r变大 B.残差平方和变大
C.变量x与变量y呈正相关 D.变量x与变量y的相关性变强
13.(2020高二下·淄博期末)下列说法正确的是( )
A.对于独立性检验,随机变量 的观测值 值越小,判定“两变量有关系”犯错误的概率越小
B.在回归分析中,相关指数 越大,说明回归模型拟合的效果越好
C.随机变量 ,若 , ,则
D.以 拟合一组数据时,经 代换后的线性回归方程为 ,则 ,
三、填空题
14.(2021·山东模拟)2021年受疫情影响,国家鼓励员工在工作地过年.某机构统计了某市5个地区的外来务工人员数与他们选择留在当地过年的人数占比,得到如下的表格:
A区 B区 C区 D区 E区
外来务工人员数 5000 4000 3500 3000 2500
留在当地的人数占比 80% 90% 80% 80% 84%
根据这5个地区的数据求得留在当地过年人员数y与外来务工人员数x的线性回归方程为 .该市对外来务工人员选择留在当地过年的每人补贴1000元,该市F区有10000名外来务工人员,根据线性回归方程估计F区需要给外来务工人员中留在当地过年的人员的补贴总额为 万元.(参考数据:取 )
15.(2018高二下·哈尔滨月考)已知线性相关的两个变量 之间的几组数据如下表:
1 2 3 4 5 6
0 2 1 3 3 4
其线性回归方程为 , 则 满足的关系式为 .
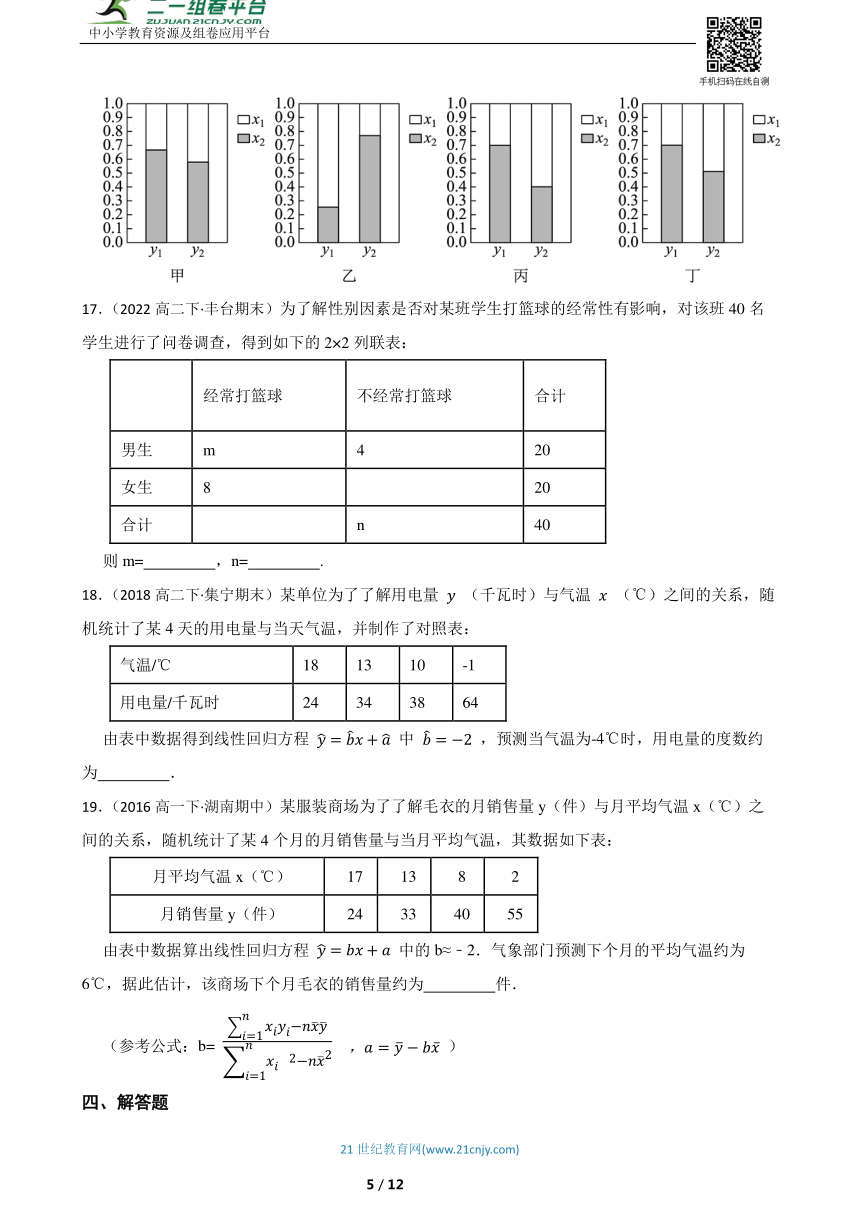
16.(2024高二下·龙岗期中)观察下面各等高堆积条形图,其中两个分类变量、相关关系最强的是 .
17.(2022高二下·丰台期末)为了解性别因素是否对某班学生打篮球的经常性有影响,对该班40名学生进行了问卷调查,得到如下的2×2列联表:
经常打篮球 不经常打篮球 合计
男生 m 4 20
女生 8 20
合计 n 40
则m= ,n= .
18.(2018高二下·集宁期末)某单位为了了解用电量 (千瓦时)与气温 (℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温/℃ 18 13 10 -1
用电量/千瓦时 24 34 38 64
由表中数据得到线性回归方程 中 ,预测当气温为-4℃时,用电量的度数约为 .
19.(2016高一下·湖南期中)某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温x(℃) 17 13 8 2
月销售量y(件) 24 33 40 55
由表中数据算出线性回归方程 中的b≈﹣2.气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月毛衣的销售量约为 件.
(参考公式:b= )
四、解答题
20.(2020高二下·聊城期末)2020突如其来的疫情让我们经历了最漫长、最特殊的一个假期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后某校进行了摸底考试,某数学教师为了调查高二学生这次摸底考试的数学成绩与每天在线学习数学的时长之间的相关关系,对在校高二学生随机抽取45名进行调查,了解到其中有25人每天在线学习数学的时长不超过1小时,并得到如下的等高条形图:
附临界值表
0.050 0.010 0.001
3.841 6.635 10.828
参考公式: ,其中 .
(1)根据等高条形图填写下面 列联表,并根据列联表判断能否在犯错误的概率不超过0.05的前提下认为“高二学生的这次摸底考试数学成绩与其每天在线学习数学的时长有关”;
数学成绩不超过120分 数学成绩超过120分 总计
每天在线学习数学不超过1小时 25
每天在线学习数学超过1小时
总计 45
(2)从被抽查的,且这次数学成绩超过120分的学生中,再随机抽取3人,求抽取的3人中每天在线学习数学的时长超过1小时的人数 的分布列与数学期望.
21.(2024高二下·保定期末)某校为了解学生阅读文学名著的情况,随机抽取了校内200名学生,调查他们一年时间内的文学名著阅读的达标情况,所得数据如下表:
阅读达标 阅读不达标 合计
女生 70 30 100
男生 40 60 100
合计 110 90 200
(1)根据上述数据,依据小概率值的独立性检验,能否认为阅读达标情况与性别有关联
(2)从阅读不达标的学生中按男、女生人数比例用分层随机抽样的方法抽取6人进行座谈,再从这6人中任选2人,记这2人中女生的人数为,求的分布列和数学期望.
附:,其中.
0.050 0.010 0.001
3.841 6.635 10.828
22.(2020高二下·阳江月考)随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 2010 2011 2012 2013 2014
时间代号 1 2 3 4 5
储蓄存款 (千亿元) 5 6 7 8 10
(Ⅰ)求y关于t的回归方程
(Ⅱ)用所求回归方程预测该地区2015年( )的人民币储蓄存款.
附:回归方程 中
23.出版商为了解某科普书一个季度的销售量y(单位:千本)和利润x(单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
序号 1 2 3 4 5 6 7 8 9 10
x 2.4 3.1 4.6 5.3 6.4 7.1 7.8 8.8 9.5 10
y 18.1 14.1 9.1 7.2 4.9 3.9 3.2 2.3 2.1 1.4
根据上述数据画出如图所示的散点图:
参考公式及参考数据:
①对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线 的斜率和截距的公式分别为 , .
②参考数据:
6.50 6.63 1.75 82.50 2.70 -143.25 -27.54
表中ui=Inxi, = .另:In4.06≈1.40.计算时,所有的小数都精确到0.01.
(1)根据图中所示的散点图判断y=ax+b和y=clnx+d哪个更适宜作为销售量y关于利润x的回归方程类型?(给出判断即可,不需要说明理由);
(2)根据(1)中的判断结果及参考数据,求出y关于x的回归方程;
(3)根据回归方程分析:设该科普书一个季度的利润总额为:(单位:千元),当季销售量y为何值时,该书一个季度的利润总额预报值最大?(季利润总额=季销售量×每本书的利润)
答案解析部分
1.【答案】A
【知识点】线性相关
2.【答案】C
【知识点】独立性检验的基本思想
3.【答案】C
【知识点】样本相关系数r及其数字特征
4.【答案】B
【知识点】线性回归方程
5.【答案】D
【知识点】独立性检验的基本思想
6.【答案】B
【知识点】线性回归方程;样本相关系数r及其数字特征
7.【答案】B
【知识点】线性回归方程
8.【答案】C
【知识点】独立性检验
9.【答案】D
【知识点】线性回归方程
10.【答案】D
【知识点】变量相关关系;散点图;线性回归方程
11.【答案】A,B,D
【知识点】独立性检验
12.【答案】A,C,D
【知识点】变量相关关系;样本相关系数r及其数字特征
13.【答案】B,D
【知识点】线性回归方程;独立性检验的应用;离散型随机变量的期望与方差
14.【答案】818.6
【知识点】线性回归方程
15.【答案】
【知识点】线性回归方程
16.【答案】乙
【知识点】线性相关
17.【答案】16;16
【知识点】线性相关
18.【答案】
【知识点】线性回归方程
19.【答案】46
【知识点】线性回归方程
20.【答案】(1)解:根据等高条形图,得 列联表
数学成绩不超过120分 数学成绩超过120分 总计
每天在线学习数学不超过1小时 15 10 25
每天在线学习数学超过1小时 5 15 20
总计 20 25 45
根据列联表中的数据,得到 的观测值
.
所以能在犯错误的概率不超过0.05的前提下认为“高二学生的这次摸底考试数学成绩与其每天在线学习数学的时长有关”.
(2)解:由列联表可得,被抽查学生中这次数学成绩超过120分的有25人,其中,每天在线学习数学的时长超过1小时的有15人,每天在线学习数学的时长不超过1小时的有10人,从中随机抽取3人,则抽取的3人中每天在线学习数学的时长超过1小时的人数 的可能取值为0,1,2,3.
, ,
, .
所以 的分布列为
所以 的数学期望 .
【知识点】独立性检验的应用;离散型随机变量及其分布列;离散型随机变量的期望与方差
21.【答案】(1)解:零假设为:阅读达标情况与性别无关,
,
根据小概率值的独立性检验,推断不成立,
即认为阅读达标情况与性别有关联;
(2)解:根据分层抽样可知:抽取的女生人数为,男生人数为,
的可能取值为,
,,,
则的分布列如下:
0 1 2
.
【知识点】分层抽样方法;独立性检验;离散型随机变量及其分布列;离散型随机变量的期望与方差;超几何分布
22.【答案】解:(I)列表计算如下
i
1 1 5 1 5
2 2 6 4 12
3 3 7 9 21
4 4 8 16 32
5 5 10 25 50
15 36 55 120
这里
又
从而 .
故所求回归方程为 .
(II)将 代入回归方程可预测该地区2015年的人民币储蓄存款为
【知识点】线性回归方程
23.【答案】(1)解:y=cln x+d更适宜作为销售量y关于利润x的回归方程类型
(2)解:令u=lnx,先建立y关于u的线性回归方程,
由于 ,
=6.63+10.20×1.75=24.48,
所以x关于u的线性回归方程为 =24.48-10.20u,
即y关于x的回归方程为 =24.48-10.20lnx.
(3)解:由题意得z=xy=x(24.48-10.20lnx),z'=[x(24.48-10.20lnx)]'=14.28-10.20lnx,
令z'=0 即14.28-10.20lnx=0,解得lnx=1.40,所以x≈4.06.
当x∈(0,4.06)时,z'>0,所以z在(0,4.06)上单调递增,
当x∈(4.06,+∞)时,z'<0,所以z在(4.06,+∞)上单调递减,
所以当x=4.06时,即季销量y=10.20千本时,季利润总额预报值最大
【知识点】线性回归方程
21世纪教育网(www.21cnjy.com)
12 / 12
高中数学人教A版(2019)选修三第八章 成对数据的统计分布
一、单选题
1.(2018高一下·河南月考)已知 是两个变量,下列四个散点图中, 呈正相关趋势的是( )
A. B.
C. D.
2.(2020高二下·阳江月考)某市政府调查市民收入与旅游愿望时,采用独立检验法抽取3000人,计算发现 ,则根据这一数据查阅下表,市政府断言市民收入增减与旅游愿望有关系的可信程度是( )
… 0.15 0.10 0.05 0.025 0.010 0.005 0.001
… 2.072 2.706 3.841 5.024 6.635 7.879 10.828
A.95% B.97.5% C.99.5% D.99.9%
3.(2024高二下·通化期中)要判断成对数据的线性相关程度的强弱,可以通过比较它们的样本相关系数r的大小,以下是四组数据的相关系数的值,则线性相关最强的是( )
A. B. C. D.
4.(2018高二下·黑龙江期中)在对具有线性相关的两个变量 和 进行统计分析时,得到如下数据:
4 8 10 12
1 2 3 5 6
由表中数据求得 关于 的回归方程为 ,则 , , 这三个样本点中落在回归直线下方的有( )个
A.1 B.2 C.3 D.0
5.(2021高二下·肇庆期末)某学校学生服务中心为了解在校学生对学校后勤工作的满意度﹐随机调查了200名学生,其中男女生比例为3:2并对这些学生进行了问卷调查,学生对后勤工作给出了满意或不满意的总体评价﹐得到下面的2×2列联表:
满意 不满意 总计
男生 104
女生 24
总计 200
附: ,其中 .
P(K2≥k0) 0.10 0.05 0.025 0.010 0.005 0.001
k0 2.706 3.841 5.024 6.635 7.879 10.828
则下列说法正确的是( )
A.2×2列联表中男生不满意的人数为18
B.2×2列联表中女生满意的人数为54
C.没有99.5%的把握认为男生与女生对后勤工作的评价有差异
D.有99.5%的把握认为男生与女生对后勤工作的评价有差异
6.(2017高二下·沈阳期末)四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程和相关系数r,分别得到以下四个结论:
①②
③④
其中,一定不正确的结论序号是( )
A.②③ B.①④ C.①②③ D.②③④
7.一台机器由于使用时间较长,但还可以使用,它按不同的转速生产出来的某机器零件有一些会有缺点,每小时生产有缺点零件的多少随机器运转的速度而变化,如表是抽样试验结果:
转速x/(rad/s) 16 14 12 8
每小时生产有缺点的零件数y/件 11 9 8 5
若实际生产中,允许每小时的产品中有缺点的零件数最多为10个,那么机器的转速应该控制所在的范围是( )
A.10转/s以下 B.15转/s以下
C.20转/s以下 D.25转/s以下
8.(2016·德州模拟)为了增强环保意识,某校从男生中随机制取了60人,从女生中随机制取了50人参加环保知识测试,统计数据如下表所示:
优秀 非优秀 总计
男生 40 20 60
女生 20 30 50
总计 60 50 110
附:x2=
P(K2≥k) 0.500 0.100 0.050 0.010 0.001
k 0.455 2.706 3.841 6.635 10.828
则有( )的把握认为环保知识是否优秀与性别有关.
A.90% B.95% C.99% D.99.9%
9.(2016高二上·鹤岗期中)某公司为确定明年投入某产品的广告支出,对近5年的广告支出m与销售额y(单位:百万元)进行了初步统计,得到下列表格中的数据:
y 30 40 p 50 70
m 2 4 5 6 8
经测算,年广告支出m与年销售额y满足线性回归方程 =6.5m+17.5,则p的值为( )
A.45 B.50 C.55 D.60
10.下表是某厂1~4月份用水量(单位:百吨)的一组数据:
月份x 1 2 3 4
用水量y 4.5 4 3 2.5
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是y=-0.7x+a,则a等于( )
A.10.5 B.5.15 C.5.2 D.5.25
二、多选题
11.(2022高三上·珠海期末)以下结论正确的是( )
A.两个随机变量的线性相关性越强,则相关系数r的绝对值越接近于1
B.在检验A与B是否有关的过程中,根据数据算得的值,越小,认为“A与B有关”的把握越小
C.随机变量,若,,则
D.在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合效果越好
12.(2022·湖北模拟)如图,5个数据,去掉点后,下列说法正确的是( )
A.相关系数r变大 B.残差平方和变大
C.变量x与变量y呈正相关 D.变量x与变量y的相关性变强
13.(2020高二下·淄博期末)下列说法正确的是( )
A.对于独立性检验,随机变量 的观测值 值越小,判定“两变量有关系”犯错误的概率越小
B.在回归分析中,相关指数 越大,说明回归模型拟合的效果越好
C.随机变量 ,若 , ,则
D.以 拟合一组数据时,经 代换后的线性回归方程为 ,则 ,
三、填空题
14.(2021·山东模拟)2021年受疫情影响,国家鼓励员工在工作地过年.某机构统计了某市5个地区的外来务工人员数与他们选择留在当地过年的人数占比,得到如下的表格:
A区 B区 C区 D区 E区
外来务工人员数 5000 4000 3500 3000 2500
留在当地的人数占比 80% 90% 80% 80% 84%
根据这5个地区的数据求得留在当地过年人员数y与外来务工人员数x的线性回归方程为 .该市对外来务工人员选择留在当地过年的每人补贴1000元,该市F区有10000名外来务工人员,根据线性回归方程估计F区需要给外来务工人员中留在当地过年的人员的补贴总额为 万元.(参考数据:取 )
15.(2018高二下·哈尔滨月考)已知线性相关的两个变量 之间的几组数据如下表:
1 2 3 4 5 6
0 2 1 3 3 4
其线性回归方程为 , 则 满足的关系式为 .
16.(2024高二下·龙岗期中)观察下面各等高堆积条形图,其中两个分类变量、相关关系最强的是 .
17.(2022高二下·丰台期末)为了解性别因素是否对某班学生打篮球的经常性有影响,对该班40名学生进行了问卷调查,得到如下的2×2列联表:
经常打篮球 不经常打篮球 合计
男生 m 4 20
女生 8 20
合计 n 40
则m= ,n= .
18.(2018高二下·集宁期末)某单位为了了解用电量 (千瓦时)与气温 (℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温/℃ 18 13 10 -1
用电量/千瓦时 24 34 38 64
由表中数据得到线性回归方程 中 ,预测当气温为-4℃时,用电量的度数约为 .
19.(2016高一下·湖南期中)某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温x(℃) 17 13 8 2
月销售量y(件) 24 33 40 55
由表中数据算出线性回归方程 中的b≈﹣2.气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月毛衣的销售量约为 件.
(参考公式:b= )
四、解答题
20.(2020高二下·聊城期末)2020突如其来的疫情让我们经历了最漫长、最特殊的一个假期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后某校进行了摸底考试,某数学教师为了调查高二学生这次摸底考试的数学成绩与每天在线学习数学的时长之间的相关关系,对在校高二学生随机抽取45名进行调查,了解到其中有25人每天在线学习数学的时长不超过1小时,并得到如下的等高条形图:
附临界值表
0.050 0.010 0.001
3.841 6.635 10.828
参考公式: ,其中 .
(1)根据等高条形图填写下面 列联表,并根据列联表判断能否在犯错误的概率不超过0.05的前提下认为“高二学生的这次摸底考试数学成绩与其每天在线学习数学的时长有关”;
数学成绩不超过120分 数学成绩超过120分 总计
每天在线学习数学不超过1小时 25
每天在线学习数学超过1小时
总计 45
(2)从被抽查的,且这次数学成绩超过120分的学生中,再随机抽取3人,求抽取的3人中每天在线学习数学的时长超过1小时的人数 的分布列与数学期望.
21.(2024高二下·保定期末)某校为了解学生阅读文学名著的情况,随机抽取了校内200名学生,调查他们一年时间内的文学名著阅读的达标情况,所得数据如下表:
阅读达标 阅读不达标 合计
女生 70 30 100
男生 40 60 100
合计 110 90 200
(1)根据上述数据,依据小概率值的独立性检验,能否认为阅读达标情况与性别有关联
(2)从阅读不达标的学生中按男、女生人数比例用分层随机抽样的方法抽取6人进行座谈,再从这6人中任选2人,记这2人中女生的人数为,求的分布列和数学期望.
附:,其中.
0.050 0.010 0.001
3.841 6.635 10.828
22.(2020高二下·阳江月考)随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 2010 2011 2012 2013 2014
时间代号 1 2 3 4 5
储蓄存款 (千亿元) 5 6 7 8 10
(Ⅰ)求y关于t的回归方程
(Ⅱ)用所求回归方程预测该地区2015年( )的人民币储蓄存款.
附:回归方程 中
23.出版商为了解某科普书一个季度的销售量y(单位:千本)和利润x(单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
序号 1 2 3 4 5 6 7 8 9 10
x 2.4 3.1 4.6 5.3 6.4 7.1 7.8 8.8 9.5 10
y 18.1 14.1 9.1 7.2 4.9 3.9 3.2 2.3 2.1 1.4
根据上述数据画出如图所示的散点图:
参考公式及参考数据:
①对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线 的斜率和截距的公式分别为 , .
②参考数据:
6.50 6.63 1.75 82.50 2.70 -143.25 -27.54
表中ui=Inxi, = .另:In4.06≈1.40.计算时,所有的小数都精确到0.01.
(1)根据图中所示的散点图判断y=ax+b和y=clnx+d哪个更适宜作为销售量y关于利润x的回归方程类型?(给出判断即可,不需要说明理由);
(2)根据(1)中的判断结果及参考数据,求出y关于x的回归方程;
(3)根据回归方程分析:设该科普书一个季度的利润总额为:(单位:千元),当季销售量y为何值时,该书一个季度的利润总额预报值最大?(季利润总额=季销售量×每本书的利润)
答案解析部分
1.【答案】A
【知识点】线性相关
2.【答案】C
【知识点】独立性检验的基本思想
3.【答案】C
【知识点】样本相关系数r及其数字特征
4.【答案】B
【知识点】线性回归方程
5.【答案】D
【知识点】独立性检验的基本思想
6.【答案】B
【知识点】线性回归方程;样本相关系数r及其数字特征
7.【答案】B
【知识点】线性回归方程
8.【答案】C
【知识点】独立性检验
9.【答案】D
【知识点】线性回归方程
10.【答案】D
【知识点】变量相关关系;散点图;线性回归方程
11.【答案】A,B,D
【知识点】独立性检验
12.【答案】A,C,D
【知识点】变量相关关系;样本相关系数r及其数字特征
13.【答案】B,D
【知识点】线性回归方程;独立性检验的应用;离散型随机变量的期望与方差
14.【答案】818.6
【知识点】线性回归方程
15.【答案】
【知识点】线性回归方程
16.【答案】乙
【知识点】线性相关
17.【答案】16;16
【知识点】线性相关
18.【答案】
【知识点】线性回归方程
19.【答案】46
【知识点】线性回归方程
20.【答案】(1)解:根据等高条形图,得 列联表
数学成绩不超过120分 数学成绩超过120分 总计
每天在线学习数学不超过1小时 15 10 25
每天在线学习数学超过1小时 5 15 20
总计 20 25 45
根据列联表中的数据,得到 的观测值
.
所以能在犯错误的概率不超过0.05的前提下认为“高二学生的这次摸底考试数学成绩与其每天在线学习数学的时长有关”.
(2)解:由列联表可得,被抽查学生中这次数学成绩超过120分的有25人,其中,每天在线学习数学的时长超过1小时的有15人,每天在线学习数学的时长不超过1小时的有10人,从中随机抽取3人,则抽取的3人中每天在线学习数学的时长超过1小时的人数 的可能取值为0,1,2,3.
, ,
, .
所以 的分布列为
所以 的数学期望 .
【知识点】独立性检验的应用;离散型随机变量及其分布列;离散型随机变量的期望与方差
21.【答案】(1)解:零假设为:阅读达标情况与性别无关,
,
根据小概率值的独立性检验,推断不成立,
即认为阅读达标情况与性别有关联;
(2)解:根据分层抽样可知:抽取的女生人数为,男生人数为,
的可能取值为,
,,,
则的分布列如下:
0 1 2
.
【知识点】分层抽样方法;独立性检验;离散型随机变量及其分布列;离散型随机变量的期望与方差;超几何分布
22.【答案】解:(I)列表计算如下
i
1 1 5 1 5
2 2 6 4 12
3 3 7 9 21
4 4 8 16 32
5 5 10 25 50
15 36 55 120
这里
又
从而 .
故所求回归方程为 .
(II)将 代入回归方程可预测该地区2015年的人民币储蓄存款为
【知识点】线性回归方程
23.【答案】(1)解:y=cln x+d更适宜作为销售量y关于利润x的回归方程类型
(2)解:令u=lnx,先建立y关于u的线性回归方程,
由于 ,
=6.63+10.20×1.75=24.48,
所以x关于u的线性回归方程为 =24.48-10.20u,
即y关于x的回归方程为 =24.48-10.20lnx.
(3)解:由题意得z=xy=x(24.48-10.20lnx),z'=[x(24.48-10.20lnx)]'=14.28-10.20lnx,
令z'=0 即14.28-10.20lnx=0,解得lnx=1.40,所以x≈4.06.
当x∈(0,4.06)时,z'>0,所以z在(0,4.06)上单调递增,
当x∈(4.06,+∞)时,z'<0,所以z在(4.06,+∞)上单调递减,
所以当x=4.06时,即季销量y=10.20千本时,季利润总额预报值最大
【知识点】线性回归方程
21世纪教育网(www.21cnjy.com)
12 / 12
