算术平方根易错点单选 归纳练 2025年中考数学一轮复习备考
文档属性
| 名称 | 算术平方根易错点单选 归纳练 2025年中考数学一轮复习备考 |  | |
| 格式 | docx | ||
| 文件大小 | 509.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-07 17:56:20 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
算术平方根易错点单选 归纳练
2025年中考数学一轮复习备考
1.下列各数中,无理数是( )
A. B.3.14159 C. D.
2.在实数﹣,,0.333……,,,,0.1010010001……中,无理数有( )
A.2个 B.3个 C.4个 D.5个
3.下列实数中的无理数是( )
A. B. C.0 D.
4.在六张卡片上分别写有,,3.1415,,0,六个数,从中随机抽取一张,卡片上的数为无理数的概率是( )
A. B. C. D.
5.下列等式一定成立的是( )
A. B. C. D.
6.下列运算正确的是( )
A. B.
C. D.
7.嘉淇做一个数学游戏,给9,5,2添加运算符号使结果等于4,如图为嘉淇所给方法,如果给一种正确的方法得25分.嘉淇的得分为( )
A.25分 B.50分 C.75分 D.100分
8.下列是无理数的是( )
A. B. C. D.
9.下列运算正确的是( )
A. B.
C. D.
10.下列计算正确的是( )
A.﹣32=9 B. C.a2 a3=a6 D.(a+b)2=a2+b2
11.如图为某同学完成的作业,他做对的题数是( )
填空: ①﹣1的倒数是(﹣1); ②|﹣3|=(3); ③3,2,4,3,6的中位数是(4); ④1,2,3,3的众数是(1.5); ⑤(﹣2); ⑥(±2).
A.6个 B.5个 C.4个 D.3个
12.下列计算正确的是( )
A. B.
C. D.
13.设,则对于实数m的范围判断正确的是( )
A. B. C. D.
14.下列命题正确的是( )
A.与是同类项,则
B.边长相等的正三角形和正四边形的外接圆半径之比为
C.、是整数,若,,则
D.的算术平方根是3
15.生活中,我们常用到长方形样、不同型号的打印纸.基于满足影印(放大或缩小后,需保持形状不变)及制作各型号纸张时,既方便又省料等方面的需要,对于纸张规格,存有一些通用的国际标准.其中,把纸定义为面积为1平方米,长与宽的比为的纸张;沿纸两条长边中点的连线裁切,就得到两张纸;再沿纸两条长边中点的连线裁切得纸…依此类推,得等等的纸张(如图所示).若设纸张的宽为米,则应为( )
A. B.的算术平方根 C. D.的算术平方根
16.已知,则下列符合条件的的值是( )
A. B. C. D.
17.下列计算中,结果正确的是( )
A. B. C. D.
18.下列计算中,结果正确的是( )
A. B. C. D.
19.下列运算结果正确的是( )
A. B.
C. D.
20.已知的三边分别为a、b、c,且,则的面积为( )
A.30 B.60 C.65 D.无法计算
21.下列等式正确的是( )
A. B. C. D.
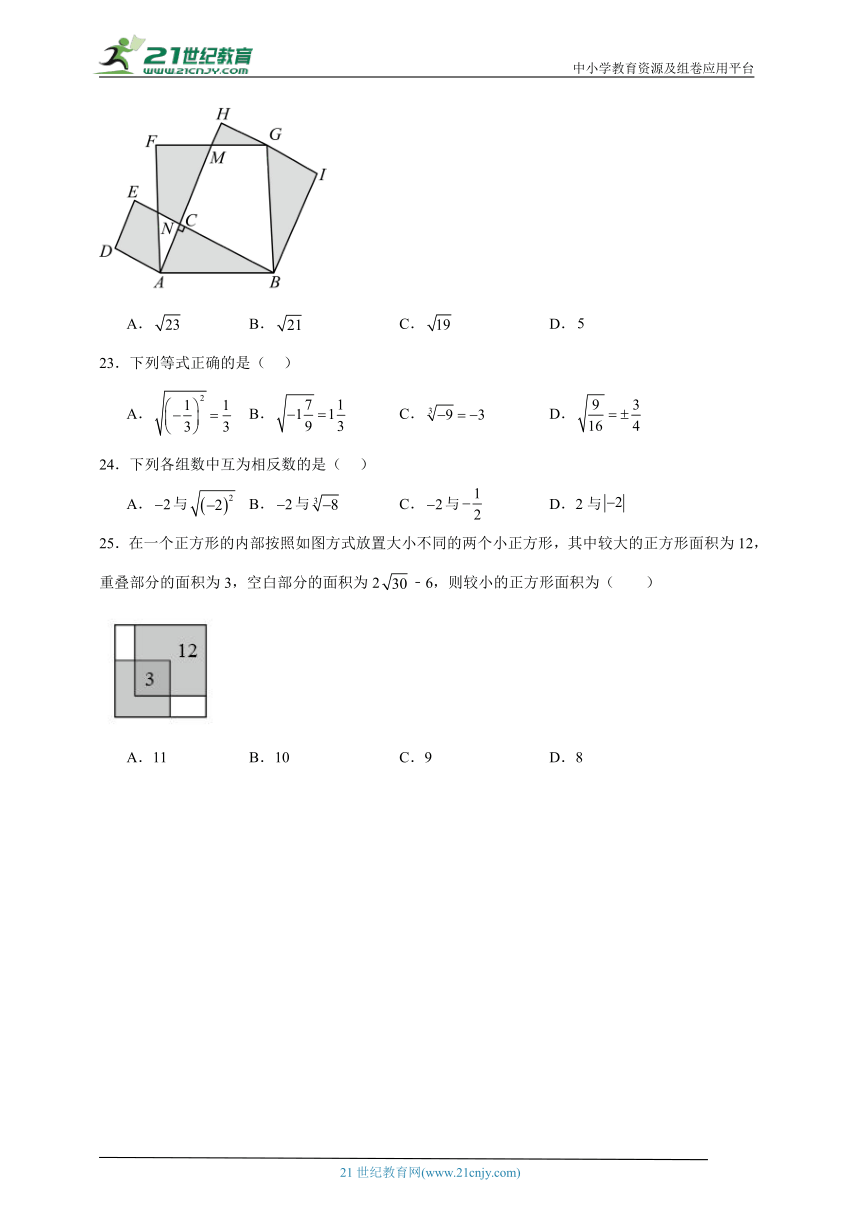
22.如图,在中,,以的各边为边作三个正方形,点落在上,若,空白部分面积为13,则的长为( )
A. B. C. D.
23.下列等式正确的是( )
A. B. C. D.
24.下列各组数中互为相反数的是( )
A.与 B.与 C.与 D.2与
25.在一个正方形的内部按照如图方式放置大小不同的两个小正方形,其中较大的正方形面积为12,重叠部分的面积为3,空白部分的面积为2﹣6,则较小的正方形面积为( )
A.11 B.10 C.9 D.8
参考答案
1.C
本题主要考查的是对无理数定义的应用,熟练掌握理解无理数的定义是解此题的关键.根据无理数的定义(无理数是指无限不循环小数)判断即可.
解:A、是分数,不是无理数,故本选项错误;
B、3.14159是小数,不是无理数,故本选项错误;
C、是无理数,故本选项正确;
D、是循环小数,不是无理数,故本选项错误;
故选C.
2.B
无限不循环小数是无理数,根据无理数的定义逐一分析即可.
解:在实数﹣,,0.333……,,,,0.1010010001……中,
都是有理数,
无理数有:
故选B
3.B
根据无理数是无限不循环小数,可得答案.
解:A.=2,2是整数,属于有理数,故本选项不符合题意;
B.是无理数,故本选项符合题意;
C.0是整数,属于有理数,故本选项不符合题意;
D.是分数,属于有理数,故本选项不符合题意.
故选:B.
4.B
首先根据无理数概念确定哪些是无理数,再根据概率的公式计算即可.
解:在,,3.1415,,0,六个数中,
无理数的有,共2个,
∴从中随机抽取一张,卡片上的数为无理数的概率是,
故选:B.
5.B
根据算术平方根和立方根的求法计算即可判断.
解:A、,故该选项计算错误,不符合题意;
B、,故该选项计算正确,符合题意;
C、,故该选项计算错误,不符合题意;
D、,故该选项计算错误,不符合题意;
故选:B.
6.C
根据算术平方根的意义、二次根式的减法、同底数幂的乘法和完全平方式逐一计算.
解:A.,选项A不符合题意;
B.,不是同类二次根式,不能合并,选项B不符合题意;
C.,选项C符合题意;
D.,选项D不符合题意;
故选:C.
7.D
根据算术平方根的计算方法、绝对值化简及有理数的乘法运算依次判断即可.
解:①;
②;
③;
④;
四种方法都正确,
∴得分为分,
故选:D.
8.D
本题主要考查无理数的定义,无理数就是无限不循环小数,理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称,即有限小数和无限循环小数是有理数,而无限不循环小数是无理数,由此即可判断选项.其中初中范围内学习的无理数有:,等;开不尽方的数;以及像0.101001000100001…等有这样规律的数.
解:A、是分数,属于有理数,故不符合题意;
B、,是整数,属于有理数,故不符合题意;
C、,是整数,属于有理数,故不符合题意;
D、是无理数,故符合题意;
故选:D.
9.C
本题考查了算术平方根的意义、绝对值、单项式乘多项式、完全平方公式.根据算术平方根的意义、绝对值、单项式乘多项式和完全平方公式逐一计算.
解:A、,本选项不符合题意;
B、,本选项不符合题意;
C、,本选项符合题意;
D、,本选项不符合题意;
故选:C.
10.B
根据乘方法则计算并判定A;根据根据二次根式性质化简并判定B;根据同底数幂相乘计算并判定C;根据完全平方公式计算并判定D.
解:A、-32=-9,故此选项不符合题意;
B、=4,故此选项符合题意;
C、a2 a3=a5,故此选项不符合题意;
D、(a+b)2=a2+2ab+b2,故此选项不符合题意;
故选:B.
11.D
①根据倒数的定义判断即可;②根据绝对值的定义判断即可;③根据中位数的定义判断即可;④根据众数的定义判断即可;⑤根据立方根的定义判断即可;⑤根据算术平方根的定义判断即可.
解:①﹣1的倒数是﹣1,正确;
②|﹣3|=3,正确;
③把数据从小到大排列为2,3,3, 4, 6,则中位数是3,故原结论错误;
④1,2,3,3的众数是3,故原结论错误;
⑤﹣2,正确;
⑥2,故原结论错误.
所以正确的有①②⑤,共3个,
故选D
12.D
本题主要考查了同分母分式加法,立方运算,算术平方根及立方根的意义,根据同分母加法运算法则以及立方的运算法则,算术平方根及立方根的意义计算判断即可.
解:A.,原计算错误,故该选项不符合题意;
B.,原计算错误,故该选项不符合题意;
C.,原计算错误,故该选项不符合题意;
D. ,原计算正确,故该选项符合题意;
故选:D.
13.C
本题考查了无理数的估算方法,根据,即可求解.
解:∵
∴
故选:C.
14.D
根据同类项的概念,二元一次方程组的解法,正多边形与圆,幂的运算,算术平方根的定义,逐项判断即可.
A、由同类项的概念得:a+2b=2,3a 4b=8,解得,,则,故此命题错误;
B、设正三角形的边长为2a,如下图所示,BD=a,∠EBD=30°,AD⊥BC,则正三角形的外接圆半径为BE=;在正方形GHPF中,由勾股定理得FH=,则正方形的外接圆半径为,则有:,故此命题错误;
C、,故此命题错误;
D、,则9的算术平方根是3,故此命题正确;
故选:D.
15.D
由纸张的宽为x米,表示出纸的宽和长,根据纸面积为1平方米求出x的值即可.
解:由图得,当纸张的宽为x米时,纸的宽为米,
∵纸张长与宽的比为,
∴纸的长为米,
∵纸面积为1平方米,
∴,
∴,
∴x的值为的算术平方根.
故选:D.
16.C
本题考查了算术平方根,根据算术平方根的定义求出的取值范围即可求解,掌握算术平方根的定义是解题的关键.
解:∵,
∴,
故选:.
17.D
根据积的乘方与幂的乘方运算,同底数幂的乘法、合并同类项,算术平方根,进行计算即可求解.
解:A. ,故该选项不正确,不符合题意;
B. ,故该选项不正确,不符合题意;
C. ,故该选项不正确,不符合题意;
D. ,故该选项正确,符合题意;
故选:D.
18.C
根据合并同类项法则、幂的乘方运算法则、开立方运算、求一个数的算术平方根,即可一一判定.
解:A.,故该选项不正确,不符合题意;
B.,故该选项不正确,不符合题意;
C.,故该选项正确,符合题意;
D.,故该选项不正确,不符合题意;
故选:C.
19.A
本题考查了同底数幂的除法,完全平分公式,二次根式的化简,合并同类项,根据整数的混合运算即可求解.
解:A、,计算正确,符合题意;
B、,原选项计算错误,不符合题意;
C、,原选项计算错误,不符合题意;
D、,原选项计算错误,不符合题意;
故选:A .
20.A
根据算术平方根、绝对值、偶次方的非负性求出a、b、c的值,根据勾股定理的逆定理得出△ABC是直角三角形,再根据三角形的面积公式求出答案即可.
∵的三边分别为a、b、c,且
∴
∴
∴
∴△ABC是直角三角形,且边c的对角∠C=90°,
∴
故选:A.
21.B
解:,故选项A错误;
,故选项B错误;
,故选项C错误;
,故选项D错误.
故选:B.
22.D
,得到四边形的面积的面积,得出空白部分的面积正方形的面积的面积,①,,②,由①和②得,即可得出答案.
解:四边形是正方形,
,,
,
,
,
,
,,
,
的面积的面积,
四边形的面积的面积,
空白部分的面积正方形的面积的面积,
①,
,
,
,
,
②,
由①和②得,
(舍去负值).
故选:D.
23.A
根据二次根式的性质、立方根和算术平方根的定义对各选项逐一进行分析即可.
解:A、,故该选项符合题意;
B、根号下是负数无意义,故该选项不符合题意;
C、无法化简,故该选项不符合题意;
D、,故该选项不符合题意.
故选:A
24.A
根据相反数的定义,化简判断即可.
A、∵,∴与互为相反数,故该项正确,符合题意;
B、∵,∴与不是相反数,故该项错误,不符合题意;
C、∵与2互为相反数,∴与不是相反数,故该项错误,不符合题意;
D、∵,∴2与不是相反数,故该项错误,不符合题意;
故选A.
25.B
根据面积可求得大正方形和阴影部分的边长,从而求得空白部分的长;观察可知两块空白部分全等,则可得到一块空白的面积;通过长方形面积公式渴求空白部分的宽,最后求出小正方形的边长即可求出面积.
∵观察可知,两个空白部分的长相等,宽也相等,
∴重叠部分也为正方形,
∵空白部分的面积为2﹣6,
∴一个空白长方形面积=,
∵大正方形面积为12,重叠部分面积为3,
∴大正方形边长=,重叠部分边长=,
∴空白部分的长=,
设空白部分宽为x,可得:,解得:x=,
∴小正方形的边长=空白部分的宽+阴影部分边长=,
∴小正方形面积==10,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
算术平方根易错点单选 归纳练
2025年中考数学一轮复习备考
1.下列各数中,无理数是( )
A. B.3.14159 C. D.
2.在实数﹣,,0.333……,,,,0.1010010001……中,无理数有( )
A.2个 B.3个 C.4个 D.5个
3.下列实数中的无理数是( )
A. B. C.0 D.
4.在六张卡片上分别写有,,3.1415,,0,六个数,从中随机抽取一张,卡片上的数为无理数的概率是( )
A. B. C. D.
5.下列等式一定成立的是( )
A. B. C. D.
6.下列运算正确的是( )
A. B.
C. D.
7.嘉淇做一个数学游戏,给9,5,2添加运算符号使结果等于4,如图为嘉淇所给方法,如果给一种正确的方法得25分.嘉淇的得分为( )
A.25分 B.50分 C.75分 D.100分
8.下列是无理数的是( )
A. B. C. D.
9.下列运算正确的是( )
A. B.
C. D.
10.下列计算正确的是( )
A.﹣32=9 B. C.a2 a3=a6 D.(a+b)2=a2+b2
11.如图为某同学完成的作业,他做对的题数是( )
填空: ①﹣1的倒数是(﹣1); ②|﹣3|=(3); ③3,2,4,3,6的中位数是(4); ④1,2,3,3的众数是(1.5); ⑤(﹣2); ⑥(±2).
A.6个 B.5个 C.4个 D.3个
12.下列计算正确的是( )
A. B.
C. D.
13.设,则对于实数m的范围判断正确的是( )
A. B. C. D.
14.下列命题正确的是( )
A.与是同类项,则
B.边长相等的正三角形和正四边形的外接圆半径之比为
C.、是整数,若,,则
D.的算术平方根是3
15.生活中,我们常用到长方形样、不同型号的打印纸.基于满足影印(放大或缩小后,需保持形状不变)及制作各型号纸张时,既方便又省料等方面的需要,对于纸张规格,存有一些通用的国际标准.其中,把纸定义为面积为1平方米,长与宽的比为的纸张;沿纸两条长边中点的连线裁切,就得到两张纸;再沿纸两条长边中点的连线裁切得纸…依此类推,得等等的纸张(如图所示).若设纸张的宽为米,则应为( )
A. B.的算术平方根 C. D.的算术平方根
16.已知,则下列符合条件的的值是( )
A. B. C. D.
17.下列计算中,结果正确的是( )
A. B. C. D.
18.下列计算中,结果正确的是( )
A. B. C. D.
19.下列运算结果正确的是( )
A. B.
C. D.
20.已知的三边分别为a、b、c,且,则的面积为( )
A.30 B.60 C.65 D.无法计算
21.下列等式正确的是( )
A. B. C. D.
22.如图,在中,,以的各边为边作三个正方形,点落在上,若,空白部分面积为13,则的长为( )
A. B. C. D.
23.下列等式正确的是( )
A. B. C. D.
24.下列各组数中互为相反数的是( )
A.与 B.与 C.与 D.2与
25.在一个正方形的内部按照如图方式放置大小不同的两个小正方形,其中较大的正方形面积为12,重叠部分的面积为3,空白部分的面积为2﹣6,则较小的正方形面积为( )
A.11 B.10 C.9 D.8
参考答案
1.C
本题主要考查的是对无理数定义的应用,熟练掌握理解无理数的定义是解此题的关键.根据无理数的定义(无理数是指无限不循环小数)判断即可.
解:A、是分数,不是无理数,故本选项错误;
B、3.14159是小数,不是无理数,故本选项错误;
C、是无理数,故本选项正确;
D、是循环小数,不是无理数,故本选项错误;
故选C.
2.B
无限不循环小数是无理数,根据无理数的定义逐一分析即可.
解:在实数﹣,,0.333……,,,,0.1010010001……中,
都是有理数,
无理数有:
故选B
3.B
根据无理数是无限不循环小数,可得答案.
解:A.=2,2是整数,属于有理数,故本选项不符合题意;
B.是无理数,故本选项符合题意;
C.0是整数,属于有理数,故本选项不符合题意;
D.是分数,属于有理数,故本选项不符合题意.
故选:B.
4.B
首先根据无理数概念确定哪些是无理数,再根据概率的公式计算即可.
解:在,,3.1415,,0,六个数中,
无理数的有,共2个,
∴从中随机抽取一张,卡片上的数为无理数的概率是,
故选:B.
5.B
根据算术平方根和立方根的求法计算即可判断.
解:A、,故该选项计算错误,不符合题意;
B、,故该选项计算正确,符合题意;
C、,故该选项计算错误,不符合题意;
D、,故该选项计算错误,不符合题意;
故选:B.
6.C
根据算术平方根的意义、二次根式的减法、同底数幂的乘法和完全平方式逐一计算.
解:A.,选项A不符合题意;
B.,不是同类二次根式,不能合并,选项B不符合题意;
C.,选项C符合题意;
D.,选项D不符合题意;
故选:C.
7.D
根据算术平方根的计算方法、绝对值化简及有理数的乘法运算依次判断即可.
解:①;
②;
③;
④;
四种方法都正确,
∴得分为分,
故选:D.
8.D
本题主要考查无理数的定义,无理数就是无限不循环小数,理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称,即有限小数和无限循环小数是有理数,而无限不循环小数是无理数,由此即可判断选项.其中初中范围内学习的无理数有:,等;开不尽方的数;以及像0.101001000100001…等有这样规律的数.
解:A、是分数,属于有理数,故不符合题意;
B、,是整数,属于有理数,故不符合题意;
C、,是整数,属于有理数,故不符合题意;
D、是无理数,故符合题意;
故选:D.
9.C
本题考查了算术平方根的意义、绝对值、单项式乘多项式、完全平方公式.根据算术平方根的意义、绝对值、单项式乘多项式和完全平方公式逐一计算.
解:A、,本选项不符合题意;
B、,本选项不符合题意;
C、,本选项符合题意;
D、,本选项不符合题意;
故选:C.
10.B
根据乘方法则计算并判定A;根据根据二次根式性质化简并判定B;根据同底数幂相乘计算并判定C;根据完全平方公式计算并判定D.
解:A、-32=-9,故此选项不符合题意;
B、=4,故此选项符合题意;
C、a2 a3=a5,故此选项不符合题意;
D、(a+b)2=a2+2ab+b2,故此选项不符合题意;
故选:B.
11.D
①根据倒数的定义判断即可;②根据绝对值的定义判断即可;③根据中位数的定义判断即可;④根据众数的定义判断即可;⑤根据立方根的定义判断即可;⑤根据算术平方根的定义判断即可.
解:①﹣1的倒数是﹣1,正确;
②|﹣3|=3,正确;
③把数据从小到大排列为2,3,3, 4, 6,则中位数是3,故原结论错误;
④1,2,3,3的众数是3,故原结论错误;
⑤﹣2,正确;
⑥2,故原结论错误.
所以正确的有①②⑤,共3个,
故选D
12.D
本题主要考查了同分母分式加法,立方运算,算术平方根及立方根的意义,根据同分母加法运算法则以及立方的运算法则,算术平方根及立方根的意义计算判断即可.
解:A.,原计算错误,故该选项不符合题意;
B.,原计算错误,故该选项不符合题意;
C.,原计算错误,故该选项不符合题意;
D. ,原计算正确,故该选项符合题意;
故选:D.
13.C
本题考查了无理数的估算方法,根据,即可求解.
解:∵
∴
故选:C.
14.D
根据同类项的概念,二元一次方程组的解法,正多边形与圆,幂的运算,算术平方根的定义,逐项判断即可.
A、由同类项的概念得:a+2b=2,3a 4b=8,解得,,则,故此命题错误;
B、设正三角形的边长为2a,如下图所示,BD=a,∠EBD=30°,AD⊥BC,则正三角形的外接圆半径为BE=;在正方形GHPF中,由勾股定理得FH=,则正方形的外接圆半径为,则有:,故此命题错误;
C、,故此命题错误;
D、,则9的算术平方根是3,故此命题正确;
故选:D.
15.D
由纸张的宽为x米,表示出纸的宽和长,根据纸面积为1平方米求出x的值即可.
解:由图得,当纸张的宽为x米时,纸的宽为米,
∵纸张长与宽的比为,
∴纸的长为米,
∵纸面积为1平方米,
∴,
∴,
∴x的值为的算术平方根.
故选:D.
16.C
本题考查了算术平方根,根据算术平方根的定义求出的取值范围即可求解,掌握算术平方根的定义是解题的关键.
解:∵,
∴,
故选:.
17.D
根据积的乘方与幂的乘方运算,同底数幂的乘法、合并同类项,算术平方根,进行计算即可求解.
解:A. ,故该选项不正确,不符合题意;
B. ,故该选项不正确,不符合题意;
C. ,故该选项不正确,不符合题意;
D. ,故该选项正确,符合题意;
故选:D.
18.C
根据合并同类项法则、幂的乘方运算法则、开立方运算、求一个数的算术平方根,即可一一判定.
解:A.,故该选项不正确,不符合题意;
B.,故该选项不正确,不符合题意;
C.,故该选项正确,符合题意;
D.,故该选项不正确,不符合题意;
故选:C.
19.A
本题考查了同底数幂的除法,完全平分公式,二次根式的化简,合并同类项,根据整数的混合运算即可求解.
解:A、,计算正确,符合题意;
B、,原选项计算错误,不符合题意;
C、,原选项计算错误,不符合题意;
D、,原选项计算错误,不符合题意;
故选:A .
20.A
根据算术平方根、绝对值、偶次方的非负性求出a、b、c的值,根据勾股定理的逆定理得出△ABC是直角三角形,再根据三角形的面积公式求出答案即可.
∵的三边分别为a、b、c,且
∴
∴
∴
∴△ABC是直角三角形,且边c的对角∠C=90°,
∴
故选:A.
21.B
解:,故选项A错误;
,故选项B错误;
,故选项C错误;
,故选项D错误.
故选:B.
22.D
,得到四边形的面积的面积,得出空白部分的面积正方形的面积的面积,①,,②,由①和②得,即可得出答案.
解:四边形是正方形,
,,
,
,
,
,
,,
,
的面积的面积,
四边形的面积的面积,
空白部分的面积正方形的面积的面积,
①,
,
,
,
,
②,
由①和②得,
(舍去负值).
故选:D.
23.A
根据二次根式的性质、立方根和算术平方根的定义对各选项逐一进行分析即可.
解:A、,故该选项符合题意;
B、根号下是负数无意义,故该选项不符合题意;
C、无法化简,故该选项不符合题意;
D、,故该选项不符合题意.
故选:A
24.A
根据相反数的定义,化简判断即可.
A、∵,∴与互为相反数,故该项正确,符合题意;
B、∵,∴与不是相反数,故该项错误,不符合题意;
C、∵与2互为相反数,∴与不是相反数,故该项错误,不符合题意;
D、∵,∴2与不是相反数,故该项错误,不符合题意;
故选A.
25.B
根据面积可求得大正方形和阴影部分的边长,从而求得空白部分的长;观察可知两块空白部分全等,则可得到一块空白的面积;通过长方形面积公式渴求空白部分的宽,最后求出小正方形的边长即可求出面积.
∵观察可知,两个空白部分的长相等,宽也相等,
∴重叠部分也为正方形,
∵空白部分的面积为2﹣6,
∴一个空白长方形面积=,
∵大正方形面积为12,重叠部分面积为3,
∴大正方形边长=,重叠部分边长=,
∴空白部分的长=,
设空白部分宽为x,可得:,解得:x=,
∴小正方形的边长=空白部分的宽+阴影部分边长=,
∴小正方形面积==10,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
